计及冰雪天气影响的风电场短期出力模型

王 浩，王洪涛，王春义



计及冰雪天气影响的风电场短期出力模型

王 浩1，王洪涛1，王春义2

(1.电网智能化调度与控制教育部重点实验室，山东大学，山东 济南 250061；2.国网山东省电力公司，山东 济南 250001)

针对冰雪天气对风电场实际运行的影响，提出了一种新的风电场短期出力模型。该模型考虑了风电机组和集电线路的积冰过程，基于现有的研究成果对叶片积冰情况下的风电机组有功出力模型进行了修正。同时考虑冰雪天气下风电场内设备的随机停运，对风电机组和集电线路在恶劣运行条件下的故障停运概率进行了估计，建立了与环境因素相依的时变停运概率模型。考虑尾流效应影响，对风电场内机组的状态进行分批次抽样，并结合机组出力水平和集电线路的抽样状态，计算风电场的出力。仿真结果表明所提的出力模型能够反映风电场在冰雪天气下短时间内的出力特性，适用于风电接入系统的短期可靠性评估。

冰雪天气；风电场；积冰模型；停运模型；状态抽样

0 引言

随着经济的增长和社会的发展，国民对电能的需求急剧增加。在资源枯竭和环境恶化的双重压力下，风力发电凭借其环境友好性和相对成熟的开发技术等优势，被公认为是最理想的可再生能源发电方式，在世界各地得到了迅速的发展。由于风能具有很强的间歇性和随机性，风电场不具备平稳输出电能的能力，这给电网带来许多新的问题，因而对风电接入系统进行可靠性评估具有非常重要的意义。其中对风电场的出力进行建模是进行此类研究的基础[1]。文献[2-8]建立了基本的风电场发电可靠性模型，考虑了风速变化、风电场风速的相关性、多种尾流效应、风机运行条件、风电机组故障停运及降额运行状态、风电场内升压变压器和集电线路的随机停运等因素。这些模型中的机组出力特性与设备故障率恒定不变，多用于评估系统中长期运行的平均可靠性水平。然而近年来频发的自然灾害对电网造成的重大影响使人们开始关注电力系统运行的短期可靠性，因而需要建立相应的风电出力短期模型。目前关于风电场的短期模型研究多集中于风电功率的一般短期预测，如基于神经网络的方法[9]、基于GA优化SVM的方法[10]、基于改进最小二乘支持向量机和预测误差校正的方法[11]等。这些方法较少考虑恶劣气象条件对风电场运行的影响，在极端气象事件的影响下，风电场内的测量控制装置有可能处于不正常工作状态，使得测量数据存在较多误差，因而针对性的预测较为困难。另外由于风电场所处环境恶劣，机组状态和故障率对天气条件的敏感性要远高于传统输变电设备，风电机组的出力能力和停运概率需要重新估计，如文献[12-13]建立了计及运行状态的风电机组短期停运模型。

综上，受极端天气状况影响，风电场短期内的出力难以用传统的风电场可靠性模型进行表征，故本文基于现有的研究成果，以冬季易发生的冰雪天气为例，建立了适用于系统短期可靠性评估的风电场出力模型。该模型考虑了冰雪天气对风机和集电线路运行的影响，能够反映风电场短时间内出力的时空分布特性，贴近风电场实际运行情况。

1  冰雪天气下风电机组出力模型

1.1 风电机组的输出功率模型

风电机组的输出功率与风速的关系曲线称为功率特性曲线，如图1所示，其表达式为

式中：为轮毂高度处的风速；in为切入风速；n为额定风速；out为切出风速；为空气密度；为叶片半径；p为风能利用系数；N为额定输出功率。标准空气密度条件下的风机功率特性曲线，称为标准功率特性曲线，可由厂家提供；在具体安装地点的风机实际出力曲线，称为实际输出功率特性曲线，修正的方法为[2]

式中：0和分别为空气密度为0和时的风机出力。由于风电场内各台机组轮毂高度处空气密度差异很小且短期内不会有较大波动，在冰雪天气持续期间采用统一恒定的空气密度进行计算。

1.2 积冰计算及对功率曲线的修正

在低温高湿度天气条件下，风电机组易发生积冰现象。积冰会改变风力机叶片的几何外形，造成叶片升力下降和阻力上升，气动性能下降，进而降低其风能利用系数，影响风机功率输出[14-15]。因此，冰雪天气下风电机组有功出力水平与风速和积冰量二者均相关，需要根据风机积冰情况对原实际功率曲线进行修正。

积冰与气象参数、积冰对象的实际属性、平均风向及设备的柔性均有关[16]，物理过程比较复杂。针对风电场环境低温及叶片结冰影响的研究，欧洲国家进行较早并获得了丰富的实验数据，建立了相应的风机积冰模拟和风机性能数值分析模型，其建立的模型虽精确但仿真过程比较复杂。本文对文献[17]中的Makkonen积冰模型进行了简化，单台风机积冰量的时变过程可以表示为

式中：turbice定义为风机积冰系数，是对风机叶片尺寸、积冰类型和积冰过程等复杂问题的简化表征，当外界环境满足积冰条件时为正值，满足融冰条件时为负值，不积冰时为0；为风速；为空气中液态水含量，可以用降水强度来近似计算，其关系[18]为

应当指出随着叶轮的旋转，积冰达到一定量后会从叶片脱离，因此叶轮存在一个最大可能积冰量，其值可以依据德国GL和风能委员会制定的风机认证指南[19]中的公式计算，如式(5)、式(6)。

式中：ice为叶中位置单位长度的积冰质量；为叶片半径；ice为积冰密度，可取为700 kg/m3；max为最大弦长；min为叶尖弦长；blade为单个叶片积冰量；为叶片数目。

详细地描述叶片积冰对风机输出功率的影响需要建立叶片三维模型，计算各个位置处的积冰厚度和形状，然后用相应的叶片气动性能计算理论对风机的输出功率进行计算，比较复杂。考虑到本文的目的，只需要表征积冰对风机出力的影响即可。文献[16]总结了4种目前的研究方法，如风洞试验及数值模拟法、风-冰-功率三维曲线图法、比较法等。本文参考芬兰VTT技术研究中心的研究成果，不同积冰情况对风机出力的影响与风机的功率控制方式有关，如图2所示[20]。

由图2可以看出，失速型风机和变速变桨距型风机在积冰情况下的输出功率均要低于正常情况且输出功率的下降程度与积冰量有关。对失速型风机，在不同风速区段因积冰导致的风机输出功率下降比例近似相同，假设输出功率下降量与积冰量为线性关系，则积冰情况下对失速型风机的功率曲线修正为

式中，1为比例系数，可由测试数据得到。

对变速变桨型风机，当积冰较少时，风机的额定风速将会增大，假设其推移量与积冰量成线性关系，在切入风速和额定风速之间的风机出力下降量也假设与积冰量为线性关系；当积冰严重时，风机的输出功率下降严重，无法达到额定功率，也采用线性处理方法，则积冰情况下对变桨型风机的功率曲线修正为

式中：2~4为比例系数；lim为表征积冰情况的阈值，可由测试数据得到。

2  冰雪天气下风电场尾流效应模型

风电场的机组布置在不同的地理位置，在计算风电场出力时需要考虑尾流效应。常见的尾流效应模型有Jensen模型、Lissaman模型、部分遮挡尾流效应模型和多重尾流效应模型等[2,4-7]。Jensen模型适用于平坦地形，在尾流影响下距离风机处的风速为

式中：0为吹向风电机组的风速；F为平坦地形的风速下降系数；T为推力系数；为叶片半径；为衰减系数。由于尾流效应与风电机组的空气动力特性有关，推力系数在风机积冰的情况下也会减小，但相比功率系数下降要小的多[21]。在此采用前述线性处理方法，积冰情况下对推力系数曲线的修正为

式中：5为比例系数，可由测试数据得到。

Lissaman模型在Jensen模型基础上考虑了风剪切的影响，适用于复杂地形。复杂地形情况下风速计算方法为

式中：V为高度处吹向风电机组的风速；为风速随高度变化的系数；C为复杂地形的风速下降系数。需要说明的是，当某一台风机停运时，由于叶轮停转，无法产生背面旋转尾流，又忽略塔架对风速的削弱效应，可认为对下游风机无影响。

3  冰雪天气下风机和集电线路停运模型

风电场中的机组数量众多，通常按一定的原则进行分组。分组后，每组内若干台风机连接于同一条中压输电线上，所有中压输电线并联连接于中压汇流母线后再统一送至升压变电站。假设风电场风机分为组，每组数量若干，采用辐射型连接方式，连接示意图如图3所示。对于辐射型连接方式，若集电线路发生故障停运，则其所连接的整组风电机组的出力将无法送出，均被迫停运。

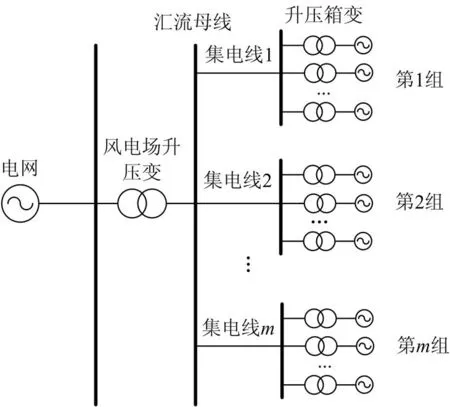
图3风机连接方式示意图

风电机组和集电线路属于暴露型设备,其主要功能部件暴露在外部环境中，导致其失效的风险因素是超过设计标准的外部环境条件，其停运为具有马尔科夫性质的随机过程[22]。由于短期可靠性评估的时间尺度较小，又考虑天气条件导致的检修环境较恶劣，本文认为风机和集电线路为不可修复元件，其运行过程用运行和停运两状态的马尔科夫链表示,如图4。

图4两状态马尔科夫过程转移示意图

图中：“0”代表运行状态，“1”代表停运状态，0和1表示两种状态之间的转移概率，对于不可修复元件，1=0。

3.1 冰雪天气下风电机组停运率时变模型

冰雪天气下风机将遭遇短时的恶劣运行环境，停运概率与特定的环境条件密切相关且明显增加，传统的故障率统计指标将不再适用。风电机组的停运主要包括受限停运和故障停运两种，其中受限停运是指风电机组运行环境如风速、温度等超出工作限值而选择暂时停机的情况，当运行环境改变后又能够重新投入运行；故障停运是指风电机组元件发生故障致使风机不能正常运行被迫停机，短时间内无法重新投入运行的情况。对于受限停运情况，风机各个时段的状态互相独立，本文认为其仍属于正常状态，只需按环境条件将风机出力设置为0即可。对于故障停运情况，风电机组的机械系统部分相对于电磁系统部分受到的影响更为显著，因此本文主要对机械系统故障停运率进行估计。

冰雪天气下风机机械系统故障停运需要考虑低温对零件韧性和油品润滑性的影响、风载荷和冰载荷对叶片和塔架的破坏等。运行经验表明，风速越大，积冰越多，温度越低，风电机组的故障率越高，因而故障停运率应表示为风速、积冰量和温度三者的函数。然而实际上建立以上函数的详细表达式依赖于对历史数据的统计分析或进行专门的测试过程，目前尚无相应的研究成果，使得冰雪天气下风电机组故障率估计十分困难。本文参考文献[4,12]中的线性处理方法，假设三种因素互相独立，风电机组的时变故障停运率表达式为

3.2 冰雪天气下集电线路停运率时变模型

冰雪天气下集电线路停运主要为故障停运。风电场的集电线路接线方式有架空线、直埋电缆和混合三种方式。本文风电场采用混合的方式，即风机与箱变、箱变与输电主干线间采用电缆，而输电主干线路采用架空线路。架空线路相比于直埋电缆受环境影响大，容易出现故障，因此本文只考虑架空线路的故障。冰雪天气下架空线路容易产生覆冰现象，进而引发绝缘子闪络、线路跳闸、断线和倒塔等事故。目前国内外已有多种模拟输电线路覆冰的数学模型，本文仍基于Makkonen积冰模型简化方法进行计算，单位长度输电线路在时间内的积冰量为

式中：lineice定义为线路积冰系数，与风机积冰系数类似；为风向与导线轴线的夹角。

架空线路覆冰过重或风激励下舞动引起断线、倒塔等故障停运的概率需要进行力学计算，比较复杂。一般认为导线覆冰质量越大、风速越大，线路发生故障停运的概率就越大。设集电线路在冰雪天气下因覆冰和舞动引起的故障停运率满足如式(14)关系。

4  冰雪天气下风电场短期出力模型

考虑到诸多测试和运行数据的不充分性及设备随机停运等因素，直接准确预测冰雪天气下的风电场出力目前难以操作[16]，这不像常规的风电功率短期预测一样具备可验证性。本文建立的风电场短期出力模型是基于随机停运事件的期望出力水平模型，目的是用于系统的短期可靠性评估。

冰雪天气对风电场的影响具有时间上的累积效应，风电机组的出力水平及机组和集电线路的故障停运率均为时变模型,本文在进行元件状态抽样时采用马尔科夫链蒙特卡洛(MCMC)方法[23]。假设冰雪天气来临之前，风电场所有机组均正常运行且无检修计划。在确定风电场机组布局后，根据输入的自然风速和风向，首先根据尾流效应模型计算风电场内各机组处的风速分布，然后根据输入的气象条件对风电场内的风机和集电线路进行积冰计算，进而根据积冰计算结果和风速水平对风机出力、机组和集电线路的故障停运率进行估计。随机抽取机组和集电线路的运行状态，从而得到整个风电场的输出功率。其中前排机组的抽样状态将影响后排机组的风速及积冰情况，进而影响后排机组的出力水平及故障停运概率，因此整个风电场机组的状态抽样是根据风向按排列逐次进行的。由于本文假设机组和集电线路为不可修复元件，当某台机组或线路的抽样状态为停运时，其后续时段的状态转移概率为0，保持停运状态，无需再进行抽样。本文利用Matlab编写程序，对计及冰雪天气影响的风电场短期出力模型进行仿真，其计算流程如图5所示。

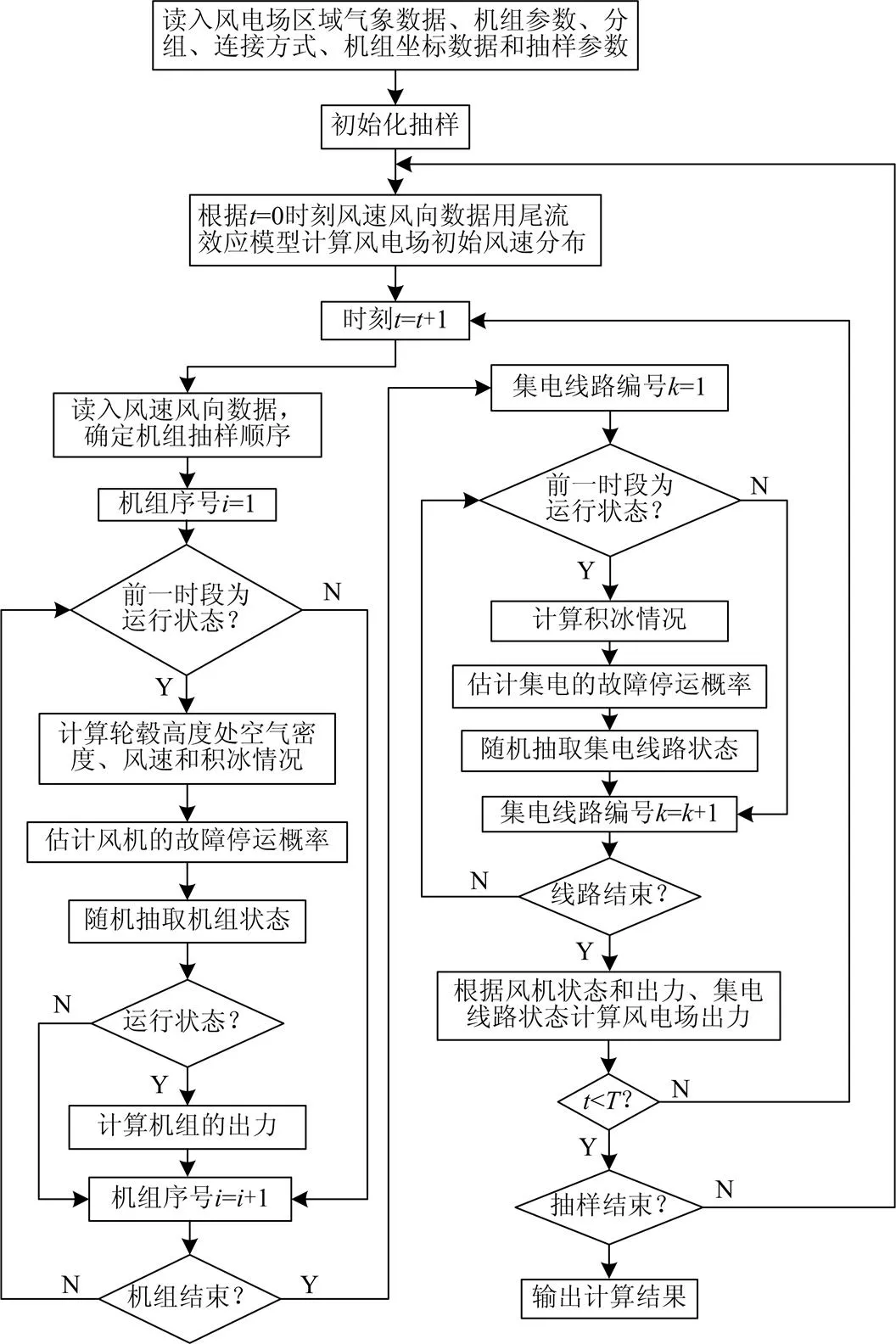
图5风电场短期出力计算流程

5  算例分析

5.1 算例数据

本文选取的算例风电场容量为75 MW，共60台风机，如图6所示，分为6组，每组10台东西排列，由6条架空集电线路送至升压变电站。风电场的风机有A(失速型，0.75 MW，轮毂高度60 m，叶轮直径50 m)、B(变桨变速型，1.5 MW，轮毂高度80 m，叶轮直径86 m)两种，其中第5、6组为A型，第1~4组为B型。两种型号风机标准功率曲线和转矩系数曲线参考某国产风机技术说明。各台机组的三维坐标附图1。风电场区域未来48 h的气温、降水量、风速和风向数据见附图2。

图6风电场机组布置和连接方式

5.2 冰雪天气下风电场风速及机组出力时空分布

风电机组的抽样状态由机组前一时段的运行状态和当前时刻的环境条件所决定；风电场内风速在单个时间断面上的空间分布主要基于机组抽样状态由尾流模型计算得到，各台机组风速的连续时间分布主要由初始风速序列和机组抽样状态确定；风电机组的出力由捕获风速、积冰情况和抽样状态三者确定。当某台机组抽样为故障停运状态时，该机组轮毂高度处的风速为0，机组出力为0。

单次抽样下，风电场内60台机组48 h内的抽样状态如图7所示，“*”代表运行，“○”代表停运，此次抽样总共有14台机组在不同的时刻发生了故障停运，当天气条件较恶劣时这在运行过程中是有可能实际存在的场景。此场景下对应的60台机组48 h内轮毂高度处捕获风速时空分布如图8所示，其中机组编号维度涵盖了同一时间断面上由尾流产生的空间效应，时间维度涵盖了同一空间断面上由风速波动和机组状态共同作用下的时间效应。由图8可以看出，在不同风向时，风电场内风速分布均匀程度不同，在某些风向下机组风速呈现明显的阶梯状，后排机组捕获到的风速衰减较为严重，在某些风向下风电场内风速较均匀，这与机组的布置方式有关。基于图8结果，综合风电机组的“风-冰-状态”信息，就计算得到了对应的机组出力时空分布特性，如图9所示。由图9可以看出，布置在不同地理位置的风机因感受到的自然环境条件不同，各自的出力也存在差异，其中包括因故障停运的机组，反映了风电场中风电机组的实际出力情况。

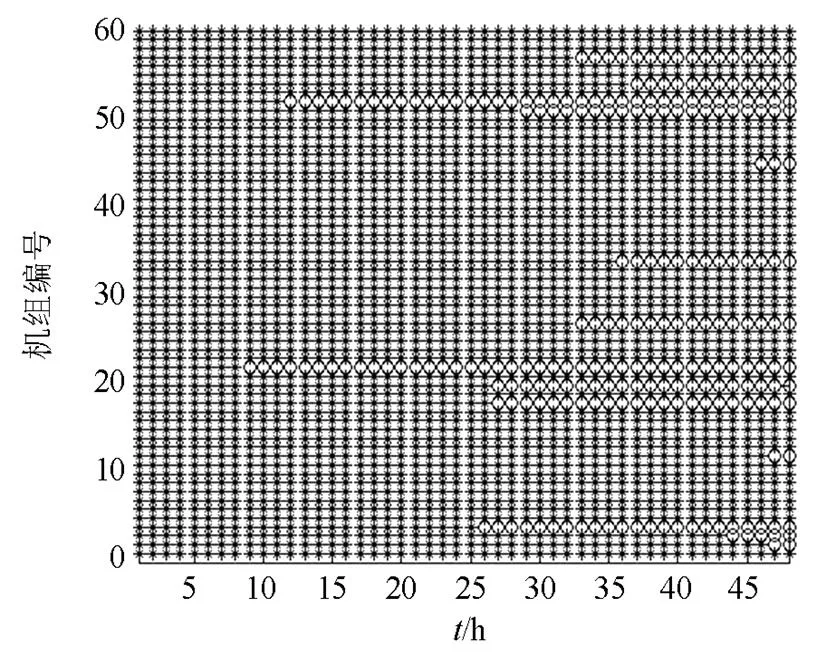
图7风电场内机组抽样状态

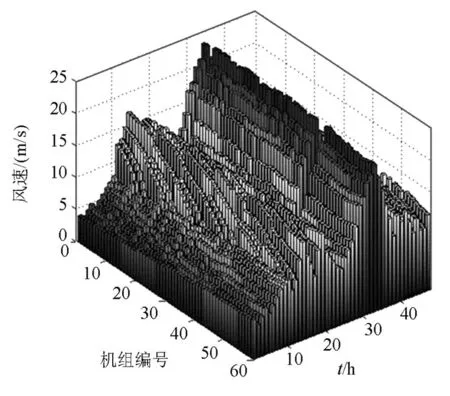
图8风电场内风速时空分布

5.3 冰雪天气下风电场出力短期特性分析

为了体现冰雪天气下风电场出力的短期特性，取4种场景进行对比分析。

场景1：不考虑积冰的影响，不考虑风电机组和集电线路的故障停运。

场景2：不考虑积冰的影响，考虑风电机组和集电线路的故障停运。

场景3：考虑积冰的影响，不考虑风电机组和集电线路的故障停运。

场景4：考虑积冰的影响，考虑风电机组和集电线路的故障停运。

其中，场景2和场景4下风电场各个时段的出力均值和方差在抽样次数达到1 000次左右即已收敛，4种场景下风电场的出力对比如图10所示。

图10 4种场景下风电场短期出力对比

由图10可以看出，在4种场景下风电场的短期出力大小不同，但波动趋势基本一致，说明短期出力的波动方向主要由风速和风向决定。在初期(0~12 h)4条出力曲线差异较小，原因是初期风速和积冰量较小，风机出力能力基本没有受到影响且机组的故障停运概率较低，各种因素对风电场出力的影响不明显。对比曲线1和2 或3和4可以看出，考虑风电机组和集电线路故障停运时风电场的短期出力水平比不考虑时要低，且后期差异较大，原因主要是本文假定风机和集电线路在短期内不可修复，在后期存在故障元件累积效果，出力能力大幅下降。对比曲线1和3或2和4可以看出，考虑冰雪天气下风机和集电线路积冰时风电场的短期出力水平比不考虑时要低，且后期差异较大，原因是冰雪天气持续期间积冰为一个逐渐累积的过程，风机出力水平随积冰量的增加逐渐受到限制。当风机积冰严重时，即使有较高风速风电场出力依旧保持在较低水平。

在第33 h时，风电场风速较高，有较多风电机组轮毂高度处的风速处于切出风速附近，属于风机出力的高敏感区段，因而风电场出力在短时间内出力水平有较大的上下波动，形成所谓的“爬坡事件”。爬坡事件对有功功率的实时平衡影响较大，严重时会造成系统事故。对比曲线1和曲线4可以看出，当此种情况发生于冰雪天气后期时，爬坡事件的爬坡幅度将因风电场出力能力的限制而降低，故对系统运行的冲击较小。综上所述，计及冰雪天气影响的风电场短期出力模型能够反映风电场在特殊天气状况下的短期出力特性，适用于系统的短期可靠性评估及预防控制。

6  结论

本文提出了一种计及冰雪天气影响的风电场短期出力模型，该模型主要包括风电机组和集电线路的简化积冰模型、风电机组有功出力积冰修正模型、机组和集电线路故障停运概率时变模型。考虑尾流效应影响，对风电场内风电机组的状态进行分时分批次抽样，结合机组出力水平和集电线路的状态抽样结果来计算风电场的出力。算例分析结果表明本文所提的可靠性模型能够反映风电场在冰雪天气下短时间内出力的时空分布特性，贴近风电场实际运行情况，适用于特殊天气状况下风电接入系统短期可靠性评估及预防控制。因实验测试数据有限，风机和集电线路的积冰过程及故障率估计中所采用的参数参考了现有的积冰仿真与故障分析结果，其合理取值有待进一步研究。

附录

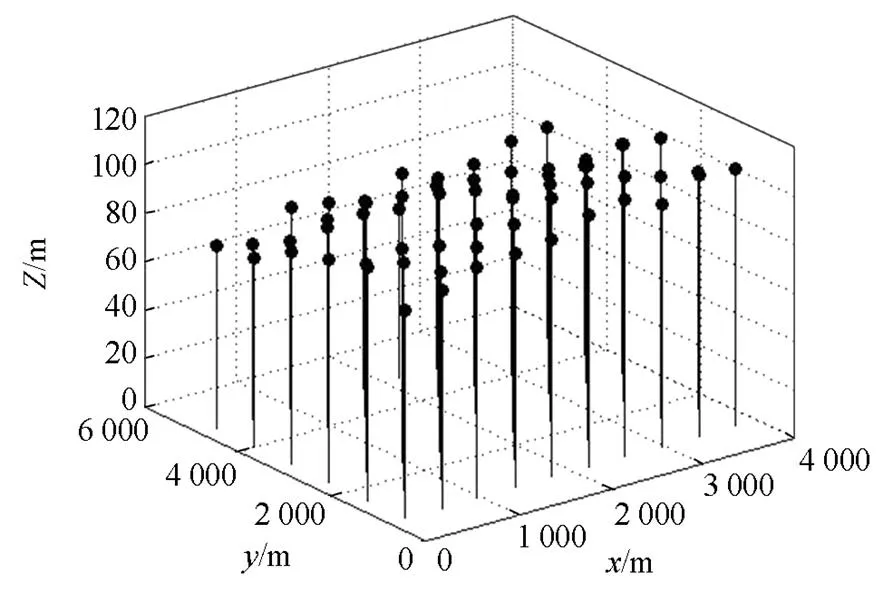
附图1风电场机组三维坐标

[1] 葛江北, 周明, 李庚银. 大型风电场建模综述[J]. 电力系统保护与控制, 2013, 41(17): 146-153.

GE Jiangbei, ZHOU Ming, LI Gengyin. Review on large- scale wind farm modeling[J]. Power System Protection and Control, 2013, 41(17): 146-153.

[2] 张硕, 李庚银, 周明, 等. 风电场可靠性建模[J]. 电网技术, 2009, 33(13): 37-41.

ZHANG Shuo, LI Gengyin, ZHOU Ming, et al. Reliability modeling of large-scale wind farms[J]. Power System Technology, 2009, 33(13): 37-41.

[3] 吴林伟, 张建华, 刘若溪. 考虑风电机组故障的风电场可靠性模型及其应用[J]. 电力系统自动化, 2012, 36(16): 31-35.

WU Linwei, ZHANG Jianhua, LIU Ruoxi. A wind farm re-liability considering wind turbine faults and its application[J]. Automation of Electric Power Systems, 2012, 36(16): 31-35.

[4] 蒋程, 刘文霞, 张建华, 等. 含风电接入的发输电系统风险评估[J]. 电工技术学报, 2014, 29(2): 260-270.

JIANG Cheng, LIU Wenxia, ZHANG Jianhua, et al. Risk assessment of generation and transmission systems considering wind power penetration[J]. Transactions of China Electrotechnical Society, 2014, 29(2): 260-270.

[5] 徐玉琴, 张林浩, 王娜. 计及尾流效应的双馈机组风电场等值建模研究[J]. 电力系统保护与控制, 2014, 42(1): 70-76.

XU Yuqin, ZHANG Linhao, WANG Na. Study on equivalent model of wind farms with DIFG considering wake effects[J]. Power System Protection and Control, 2014, 42(1): 70-76.

[6] 仇国兵, 刘文霞, 张建华. 考虑复杂尾流效应和连接电缆故障的风电场可靠性建模[J]. 电力系统自动化, 2014, 38(18): 33-39, 64.

QIU Guobing, LIU Wenxia, ZHANG Jianhua. Reliability modeling of wind farms considering complex wake effects and connecting cable failures[J]. Automation of Electric Power Systems, 2014, 38(18): 33-39, 64.

[7] 孙辉, 徐箭, 孙元章, 等. 考虑风速时空分布及风机运行状态的风电场功率计算方法[J]. 电力系统自动化, 2015, 39(2): 30-38, 60.

SUN Hui, XU Jian, SUN Yuanzhang, et al. A method for wind power calculation considering wind speed spatial and temporal distribution and wind turbine operation status[J]. Automation of Electric Power Systems, 2015, 39(2): 30-38, 60.

[8] CHEN Fan, LI Fangxing, WEI Zhinong, et al. Reliability models of wind farms considering wind speed correlation and WTG outage[J]. Electric Power Systems Research, 2015, 119: 385-392.

[9] 袁铁江, 晁勤, 李义岩, 等. 大规模风电并网电力系统经济调度中风电场出力的短期预测模型[J]. 中国电机工程学报, 2010, 30(13): 23-27.

YUAN Tiejiang, CHAO Qin, LI Yiyan, et al. Short-term wind power output forecasting model for economic dispatch of power system incorporating large-scale wind farm[J]. Proceedings of the CSEE, 2010, 30(13): 23-27.

[10]刘爱国, 薛云涛, 胡江鹭, 等. 基于GA优化SVM的风电功率的超短期预测[J]. 电力系统保护与控制, 2015, 43(2): 90-95.

LIU Aiguo, XUE Yuntao, HU Jianglu, et al. Ultra-short- term wind power forecasting based on SVM optimized by GA[J]. Power System Protection and Control, 2015, 43(2): 90-95.

[11]李霄, 王昕, 郑益慧, 等. 基于改进最小二乘支持向量机和预测误差校正的短期风电负荷预测[J]. 电力系统保护与控制, 2015, 43(11): 63-69.

LI Xiao, WANG Xin, ZHENG Yihui, et al. Short-term wind load forecasting based on improved LSSVM and error forecasting correction[J]. Power System Protection and Control, 2015, 43(11): 63-69.

[12] 蒋程, 张建华, 刘先正, 等. 计及运行工况的风电机组停运模型[J]. 电力系统保护与控制, 2013, 41(24): 112-116.

JIANG Cheng, ZHANG Jianhua, LIU Xianzheng, et al. Wind turbine outage model based on operation conditions[J]. Power System Protection and Control, 2013, 41(24): 112-116.

[13] 李剑, 雷潇, 冉立, 等. 一种计及运行状态的风电机组短期停运模型[J]. 中国电机工程学报, 2015, 35(8): 1845-1852.

LI Jian, LEI Xiao, RAN Li, et al. A short-term outage model of wind turbines considering operating conditions[J]. Proceedings of the CSEE, 2015, 35(8): 1845-1852.

[14] VIRK M S, HOMOLA M C, NICKLASSON P J. Effect of rime ice accretion on aerodynamic characteristics of wind turbine blade profiles[J]. Wind Engineering, 2010, 34(2): 207-218.

[15] HOMOLA M C, VIRK M S, NICKLASSON P J, et al. Performance losses due to ice accretion for a 5 MW wind turbine[J]. Wind Energy, 2012, 15(3): 379-389.

[16] 王聪, 黄洁亭, 张勇, 等. 风电机组叶片结冰研究现状与进展[J]. 电力建设, 2014(2): 70-75.

WANG Cong, HUANG Jieting, ZHANG Yong, et al. Status and advance in research on blade icing of wind turbines[J]. Electric Power Construction, 2014(2): 70-75.

[17] MAKKONEN L, LAAKSO T, MARJANIEMI M, et al. Modeling and prevention of ice accretion on wind turbines[J]. Wind Engineering, 2001, 25(1): 3-21.

[18] BEST A C. The size distribution of raindrops[C]. Quart J Royal Met Soc, 1949: 16-36.

[19] CERTIFICATION G L R. Guideline for the Certification of Wind Turbines[EB/OL]. [2015-07-07]. http:// cvi.se/ uploads/pdf/Master%20Literature/Wind%20Turbine%20Technology/Guideline_for_the_Certification_of_Wind_Turbines_Edition_2010_R0_2_.pdf.

[20] IAN B, MICHAEL D, ANDREAS K, et al. Wind energy projects in cold climates[EB/OL]. [2015-07-07]. https:// www.ieawind.org/index_page_postings/June%207%20posts/task%2019%20cold_climate_%20rp_approved05.12.pdf.

[21] MAHMOUD E, MARTIN O L H, TORGEIR M. Atmospheric ice accumulation and its effect on a typical 5MW wind turbine in different operational conditions [EB/OL]. [2015-07-07]. http:// proceedings.ewea.org/ offshore2011/proceedings/Posters/PO_110_EWEAOffshore2011presentation.pdf.

[22] 宁辽逸, 吴文传, 张伯明. 电力系统运行风险评估中元件时变停运模型分析[J]. 电力系统自动化, 2009, 33(16): 7-12.

NING Liaoyi, WU Wenchuan, ZHANG Boming. Analysis of a time-varying power component outage model for operation risk assessment[J]. Automation of Electric Power Systems, 2009, 33(16): 7-12.

[23] 石文辉, 别朝红, 王锡凡. 大型电力系统可靠性评估中的马尔可夫链蒙特卡洛方法[J]. 中国电机工程学报, 2008, 28(4): 9-15.

SHI Wenhui, BIE Zhaohong, WANG Xifan. Application of Markov chain Monte Carlo in large-scale system reliability evaluation[J]. Proceedings of the CSEE, 2008, 28(4): 9-15.

(编辑 葛艳娜)

A short-term output model of wind farm considering rain-snow-ice weather

WANG Hao1, WANG Hongtao1, WANG Chunyi2

(1. Key Laboratory of Power System Intelligent Dispatch and Control of Ministry of Education, Shandong University, Jinan 250061, China; 2. State Grid Shandong Electric Power Company, Jinan 250001, China)

Considering the impacts of rain-snow-ice weather on wind farm practical operation, this paper proposes a new short-term output model of wind farm. This model considers the ice accretion on wind turbines and transmission lines. The power output models of wind turbines with ice on blades are modified based on existing studies. The outage of facilities in wind farm is also considered in this model. The outage probability of wind turbines and transmission lines under bad conditions is estimated and a time varying model is established. Considering the wake effect, the states of wind turbines are sampled sequentially. Combined with the output level of wind turbines and the states of transmission lines, the power output of wind farm is calculated. Simulation result shows that the proposed model can reflect the short-term characteristics of wind farm output and can be used for short-term reliability assessment of power system.

This work is supported by National Basic Research Program of China (973 Program) (No. 2012CB215101) and National Natural Science Foundation of China (No. 51177092).

rain-snow-ice weather; wind farm; ice accretion model; outage model; state sampling

10.7667/PSPC150978

2015-06-11；

2015-07-13

王 浩(1990-)，男，硕士研究生，研究方向为风力发电与并网；E-mail: joeldream@163.com

王洪涛(1973-)，男，通信作者，博士，教授，博士生导师，研究方向为电力系统恢复控制，风力发电与并网等；E-mail: whtwhm@sdu.edu.cn

王春义(1980-)，男，博士，高级工程师，研究方向为电力系统规划运行和分析。

国家重点基础研究发展计划项目(973计划) (2012CB215101)；国家自然科学基金项目(51177092)