汽车线控转向实验台转向驱动系统的辨识及其PID控制

余颖弘，王保华

（湖北汽车工业学院汽车工程学院，湖北十堰442002）

汽车线控转向实验台转向驱动系统的辨识及其PID控制

余颖弘，王保华

（湖北汽车工业学院汽车工程学院，湖北十堰442002）

对本课题组采用的转向驱动系统进行机电分解，推导得到系统传递函数结构。基于Matlab系统辨识工具箱，辨识得到其传递函数，对比实物试验数据，验证了辨识传函正确性。利用Matlab/Simulink对辨识传递函数进行离线PID整定。对比实物试验与仿真结果，结果表明2组试验阶跃响应指标误差在1.44%左右。通过此方法可缩短PID整定时间，减轻实验人员工作量。

转向驱动系统；线控转向实验台；系统辨识；PID控制

汽车线控转向（steering-by-wire，SBW）硬件在环实验台具有很高的仿真度，可以灵活地进行一些实际中不可能或不易进行的实验，是介于虚拟软件仿真和实物实验之间的重要实验方式［1］。其中转向驱动系统作为实验台的重要硬件组成，对其控制好坏直接影响实验台的仿真精度。

转向驱动系统也是线控转向系统的重要硬件组成，由电控单元（ECU）、转向驱动器、信号传感器3个部分组成，如图1所示。当ECU获取上位机发送的车速、目标转角等整车状态信号时，结合角位移传感器采集的转角信号进行误差处理计算，得到相应的PWM信号，并驱动转向驱动系统的电机，经过蜗轮蜗杆、齿轮齿条2级机械减速机构，拉动转向节臂带动转向轮转动相应的转角。

在系统控制策略设计中，控制器参数的确定主要有工程方法和理论方法。工程方法不用建模，但存在调试困难、不易得到最佳效果等缺点，且真机调试消耗资源，甚至可能损坏设备。本文中在对转向驱动系统的控制中，拟采用理论方法来克服这些缺点，基于Matlab系统辨识工具箱对某国外EPS转向梯形硬件进行系统辨识，得到转向驱动系统数学模型。利用Matlab/Simulink离线整定出对此传递函数有效控制的PID参数。

图1　SBW硬件在环实验台转向驱动系统组成图

1　转向驱动系统数学模型结构

根据转向驱动系统各模块输入及输出（图2），对其机电结构分解分析可知，该系统包括电机模块、机械减速机构、齿条/拉杆/转向轮机械连接模块3个部分。本节中将对上述3个组成分别讨论，最后确定转向驱动系统的传递函数结构，为后文中系统传递函数的确定提供理论支撑。

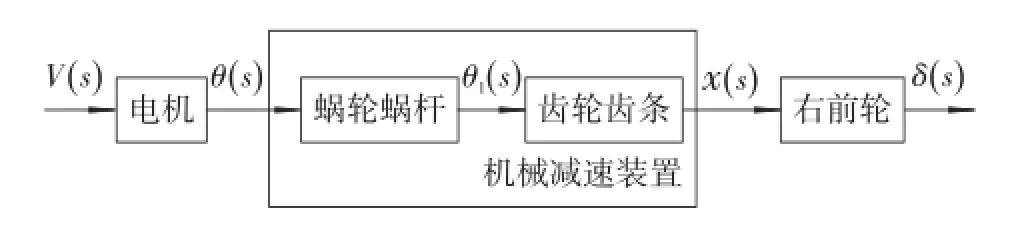
图2　SBW实验台转向系统模型简图

1.1电机模块

前期试验过程中，在直流电源作用下，电机工作且电机空转转速与电压之间存在正比关系，得知此EPS驱动电机为直流电机。根据直流电机知识得到电机模块传递函数［2］：

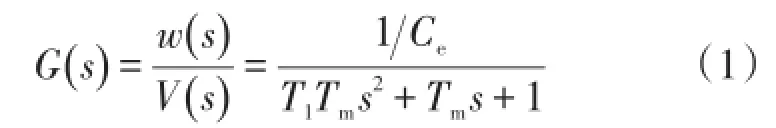
式中：w（s）为电机角速度的拉普拉斯变换，（°）·s-1； Vs为电机加载电压的拉斯变换，V；T1为电磁时间常数；Tm为机械时间常数；Ce为反电势常数。

由于线控转向的控制中，角度作为控制量，需要得到角度θ（s）关于电压V（s）的变化关系，将角度与角速度关系式（2）代入式（1）中，得到直流电机转角θ（s）关于电压V（s）变化的传递函数（式（3））。

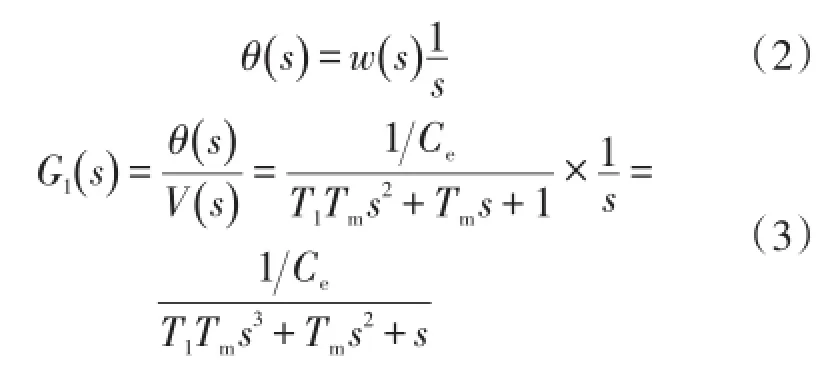
1.2机械减速装置

在该型EPS的转向梯形上，电机转角经过2级减速装置，使齿条发生横向位移。其中电机转轴固连蜗杆带动蜗轮转动，减速比为i1；蜗轮转轴末端小齿轮带动齿条横向运动，减速比为i2；整体减速比为i，表达式为

1.3齿条/拉杆/转向轮机械连接模块

为探究右前轮转角δ（s）与横向位移x（s）的运动关系，结合图1对其机械运动组成进行分析可知：齿条横向运动带动转向横拉杆，拉动转向节臂，使得转向节绕主销转动。通过对齿条、转向横拉杆、转向节臂、机架组成机械分解，由其运动形式可知此结构为四杆机构，简化并绘制其机械运动简图如图3所示。此四杆机构中各组成杆件具体数值如表1所示。

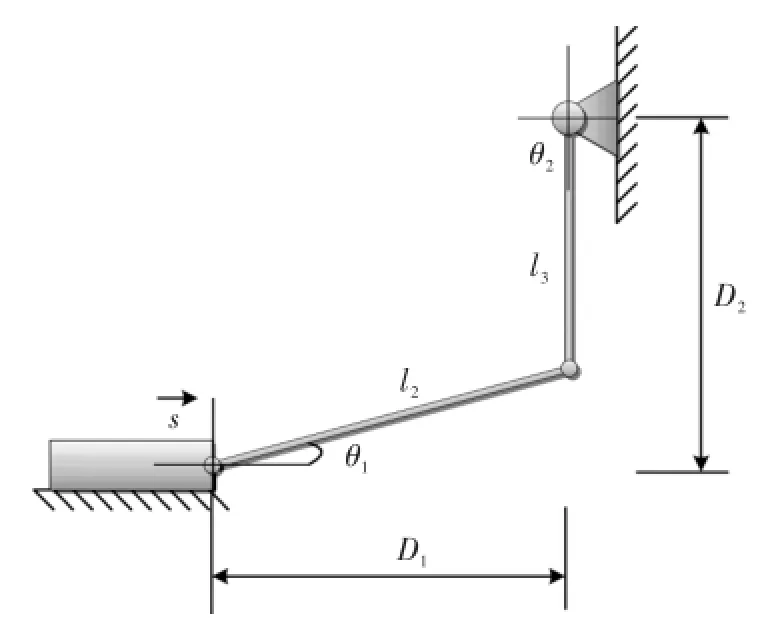
图3　齿条/拉杆/转向轮机械连接模块运动简图

根据运动简图，对其进行运动学分析，得到：

表1　齿条/拉杆/转向轮机械连接模块运动部件参数 m

由式（5）得到θ1关于θ2的表达式：

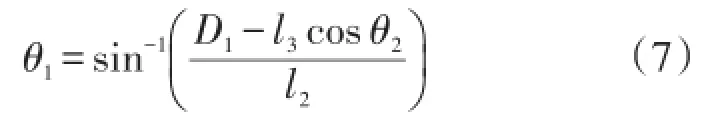
再将式（7）代入式（5），得到s与θ2的关系式：

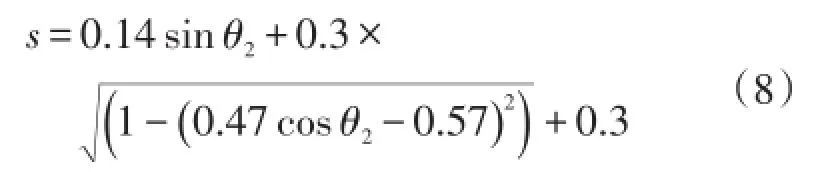
取其反函数并绘制右前轮转角θ2关于齿条位移s的关系曲线，见图4。由图4可知：右轮转角θ2关于齿条行程s变化的曲线线性度较高，可视为定比环节，斜率为k，见式（9）。

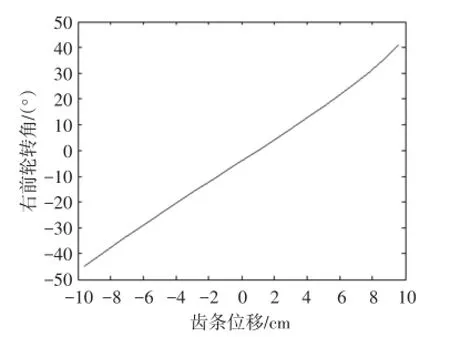
图4　θ2关于s的关系曲线

故在针对线控转向硬件在环实验台转向驱动系统无阻力的开环位置控制中，在电压V的驱动下，其前轮发生转向δ的传递函数H（s）可表示为

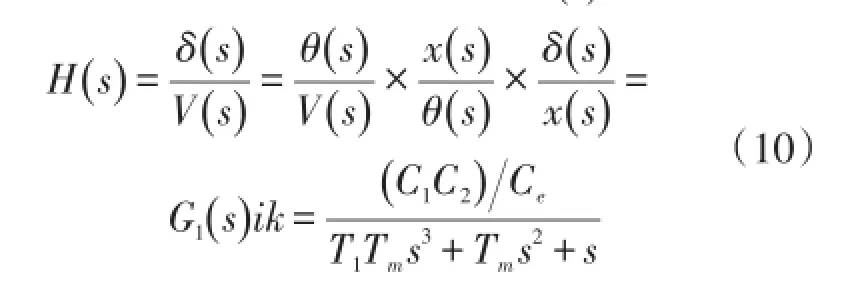
可知，转向驱动系统传递函数结构为3阶函数。

2　基于Matlab系统识别及验证

根据位置反馈实验数据进行转向驱动系统辨识。考虑到系统的时变和干扰性，进行多组实验，在目标应用程序实时运行过程中，通过改变输入正弦波信号的振幅和频率、方波信号的持续时间及幅值，进行参数的交互式调整，对参数的改变将立即反映到线控转向实验台右前轮输出信号上，记录下输出数据［3-4］。在Matlab环境下，将采集到的各组输入、输出数据导入，进行预处理，数据分成2个部分：一部分用作工作数据进行模型辨识，另一部分用作验证数据。实验中分别采用ARX（自回归外生）模型和状态空间模型，系统辨识过程中，参照辨识工具箱中各模型的贴合度，如图5所示。

图5辨识结果与实验数据的逼近程度图

图5中利用ARX模型辨识结果与原始实验数据逼近程度为98.8%，状态方程模型辨识结果逼近程度为97.77%，最终采用ARX模型。转向驱动系统模型结构为3阶系统，将辨识结果转换成传递函数形式：

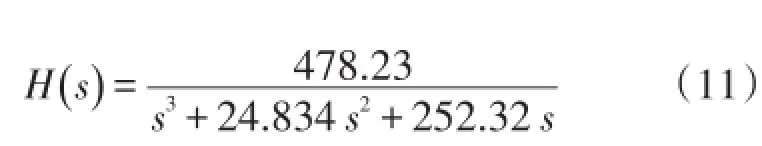
对辨识转化得到的传递函数，进行离线仿真，设置与实验相同的方波信号，得到输出前轮转角运动曲线，与实物实验的数据运动关系表现几乎一致（图6），验证了辨识模型正确性。

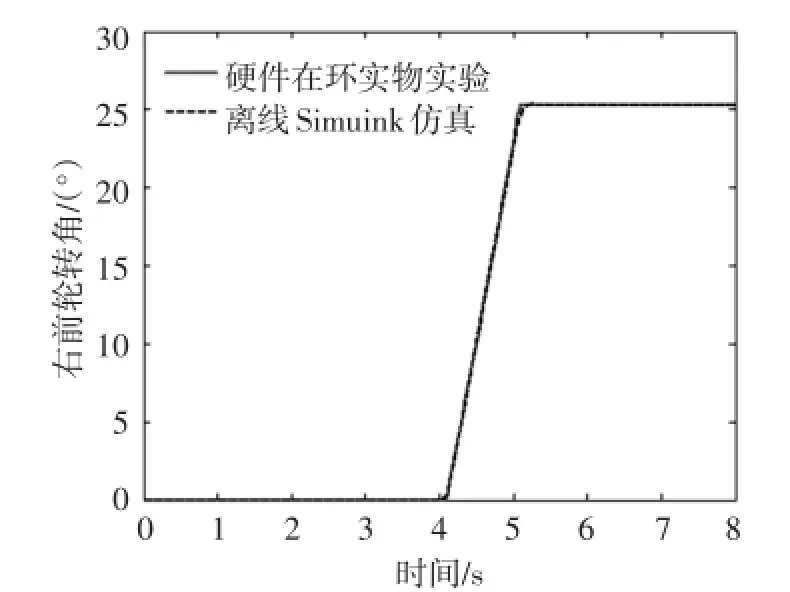
图6　同一方波信号作用下2组试验响应曲线对比图

3　基于模型传递函数的PID整定

在转向驱动系统控制策略设计中，利用理论方法，由转向驱动系统辨识结果，以经典PID控制作为转向驱动系统控制方法，对式（11）所示传递函数进行位置闭环控制的离线仿真并整定PID参数。

在Matlab/Simulink环境下，对式（11）以前轮转角作为目标进行PID控制。利用PID模块自动整定功能，综合考虑经过PID控制输出结果的鲁棒性及其时域响应特性，得到kp为6.26，ki为0.29，kd为0.38，N为7.94。将此组PID参数设置到线控转向硬件在环实验台转向驱动系统的控制器中，设置相同的期望转角进行实物实验及Simulink离线仿真，观察经过PID处理后前轮转角的变化。对比图7中实物实验和Simulink离线仿真结果，前轮转角都最终到达了期望转角位置。对其时域变化数据汇总，如表2所示。

图7　PID控制下2组试验的阶跃响应曲线

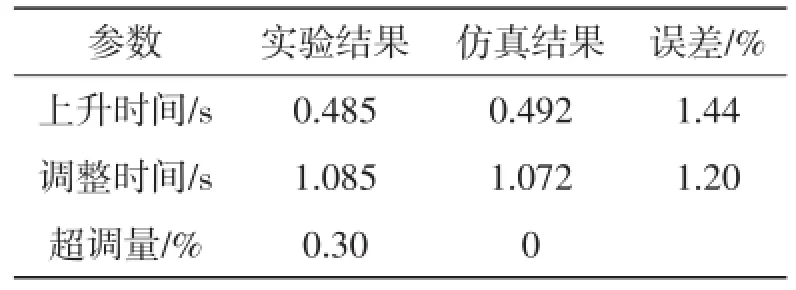
表2　PID控制下2组实验的阶跃响应指标

观察图7曲线及表2数据，2组实验在PID控制下都较为迅速地稳定到了期望转角，实现了PID控制目标，且2组实验的上升时间、调整时间误差较小，误差在1.44%左右，证明了对转向驱动系统辨识的正确性。

4　总结

在对一陌生系统的控制策略设计中，采用理论方法，通过对系统机电分解、系统辨识、离线仿真，确定了1组能对系统有效控制的PID参数。具体工作如下：1）机电分解，分解得到硬件在环实验台转向驱动系统运动部件组成，确定了该系统传递函数结构；2）系统辨识，基于实验数据和ARX、状态空间辨识模型，结合系统传递函数结构，辨识得到转向驱动系统数学模型，通过与实验数据对比，验证了辨识正确性；3）离线仿真，在Simulink环境下对系统数学模型进行PID控制，自动整定到一组能够对系统较好控制的PID参数，通过实物实验与离线仿真结果比对，2组实验结果误差仅在1.44%左右，验证了离线仿真整定的正确性。

综上，在对系统的控制策略设计中，基于系统辨识得到系统数学模型并通过Simulink整定PID控制参数的理论方法，可以较快对一个陌生系统进行PID控制，缩短PID整定时间，减小实验设备损毁风险，减轻实验人员工作量。

［1］余颖弘，王保华.汽车线控转向硬件在环实验台研究现状综述［J］.湖北汽车工业学院学报，2015，29（3）：34-38.

［2］高远.基于预测函数控制的无刷直流电机转速控制［D］.沈阳：东北大学，2013.

［3］张立勋，董玉红，王怀军.基于半物理仿真技术的机电伺服系统模型辨识研究［J］.机电一体化，2006，22（2）：30-32.

［4］朱建新，赵崇友，邹湘伏.液压挖掘机振动掘削土体参数在线辨识［J］.中南大学学报（自然科学版），2006 （3）：537-541.

［5］丁洋，王保华，麻友良.基于dSPACE/CarSim的SBW硬件在环仿真平台开发［J］.湖北汽车工业学院学报，2013，27（2）：5-10.

Identification and PID Control of Steering Drive System for Vehicle Steer-by-wire Test Bench

Yu Yinghong，Wang Baohua
（School of Automotive Engineering，Hubei University of Automotive Technology，Shiyan 442002，China）

The steering drive system used in the research group was mechanically and electrically disas⁃sembled and analyzed，the structure of the system transfer function was derived.Based on Matlab Sys⁃tem Identification Toolbox，the transfer function was identified and obtained.Compared with the physi⁃cal test data，the correctness of identification of the transfer function was verified.Based on Matlab/ Simulink，the PID control parameters of the transfer function were tuned offline.The physical test and simulation results were compared.The results show the two experimental step response error indicators is around 1.44%.By this method，PID tuning time can be shortened and laboratory personnel workload can be reduced.

steering drive system；steer-by-wire test bench；system identification；PID control

U467.5+2

A

1008-5483（2016）02-0001-04

10.3969/j.issn.1008-5483.2016.02.001

2016-04-27

湖北省科技支撑计划项目（2015BAA046）；湖北省自然科学基金项目（2013CFA134）；汽车动力传动与电子控制湖北省重点实验室项目（ZDK201214）

余颖弘（1991-），男，湖北荆州人，硕士生，从事汽车动力学仿真与控制研究。E-mail：79824220@qq.com