基于切向滚齿加工斜齿轮修形齿面的设计与分析

蒋进科，方宗德



基于切向滚齿加工斜齿轮修形齿面的设计与分析

蒋进科，方宗德

(西北工业大学机电学院，陕西西安，710072)

为提高修形齿轮加工效率，并降低齿轮副振动与噪音，提出切向滚齿加工双鼓形齿斜齿轮设计方法。根据空间啮合原理建立3自由度切向滚齿模型，设计滚刀齿形及修正工件附加转交角与安装中心距，并推导工件修形齿面；其次，结合LTCA技术以承载传动误差(LTE)幅值最小为优化目标，获得上述加工参数，并分析LTE幅值与齿轮副重合度关系。研究结果表明：设计加工参数可减小安装误差敏感性，避免边缘接触；齿轮副LTE幅值降低44%，因此，有利于降低振动与噪音；当滚刀有齿向修形时，再增加合理的切向运动，使得滚切过程中，产生沿齿向方向齿形的连续变化，可消除传统加工(改变中心距)产生的齿形扭曲。

滚齿；拓扑修形；接触分析；承载接触分析；承载传动误差

滚齿加工是一种高效、经济的圆柱齿轮加方法，广泛应用于直齿、斜齿、蜗轮齿面加工。随着现代数控滚齿技术发展，滚齿加工精度、效率明显提高，国外高档数控滚齿机加工精度已达4级，通过控制机床运动及修形滚刀齿面可以加工出新颖有拓扑修形齿面工件，提高了平行轴渐开线齿面传动质量。切向滚齿在切削过程中，除沿工件轴向进给外，还增加1个沿滚刀本身轴线方向的切向进给运动，为3自由度加工，其优点是滚刀在全长内的所有刀齿都参与切削，使各刀齿的负荷均匀, 刀具耐用度提高，齿面光洁度和精度高。滚齿啮合原理类似1对交错轴渐开线齿轮传动。CHIU等[1]研究表明即使在切削条件良好条件下，滚齿齿面误差主要来源于滚刀几何设计误差及加工中心距误差。NAGATA[2]建立了通用6轴CNC滚齿机模型，研究了多自由度滚齿加工技术，推导了机床各轴运动关系。为了提高滚齿加工效率，BOUZAKIS等[3−4]通过试验分析，建立了滚刀磨损量计算模型，预算了滚刀磨损量。VEDMAR[5]假设滚刀切削刃在任意方向为平面曲线，通过函数解析方法得到工件可能的形貌，预算工件齿面粗糙度。INNOCENTI[6]通过分析计算得到滚齿安装参数(轴交角与中心距)、啮合侧隙简单关系，为了实现0侧隙啮合，得到最佳安装参数。XIA等[7]通过四轴联动实现切向滚齿加工非圆齿轮。HSU等[8−10]建立了2自由度滚齿模型，通过改变滚刀齿厚、切向进给参数、工件附加转角，实现齿向无扭曲齿面加工，并进行了齿向鼓形齿分析(TCA)。RADZEVICH等[11−14]通过对滚刀几何设计及运动学分析，确定了滚齿过程轴向进给最小空行程距离，并在分析计算滚刀切削刃参数基础上对其几何参数、机床加工参数进行优化，提高了滚刀加工齿面精度。 为了提高滚刀加工精度，SHIH等[15]建立了CNC 5轴联动滚刀前刀面高阶校正模型，通过最小二乘法获得机床运动参数。上述研究局限于加工标准齿面的滚刀几何设计与分析，尚未涉及滚齿拓扑修形齿面及齿面啮合性能研究。现代数控技术的发展使得通过控制机床运动及修形滚刀齿形，实现滚齿拓扑修形齿面的加工达到减振降噪效果已成为可能。齿轮承载传动误差(LTE)已被证实是产生振动与噪音的主要因素[16−17]，WANG等[18]通过预设4阶UTE及接触路径，根据局部综合法推导弧齿锥齿轮加工参数。SIMON等[19−20]介绍一种承载接触分析(LTCA)模型，通过优化机床径向运动、滚轮运动系数，使LTE幅值降低了70%~80%，但并未报道优化方法。ARTONI等[21]通过优化准双曲面LTEs幅值及齿面应力最小，得到减材料齿面最佳修形量。因此，如何通过设计滚齿加工参数进行修形齿面加工，降低齿轮副LTE幅值，达到减振降噪效果有重要意义。本文作者根据空间啮合原理建立3自由度切向滚齿模型，通过设计滚刀齿形及修正工件附加转交角、中心距、切向进给速度，推导工件拓扑修形齿面；结合LTCA技术以LTE幅值最小为优化目标，获得滚刀齿形修形及运动参数。

1 齿条展成渐开线齿面

传统滚刀齿面为渐开线齿面，为了加工修形齿面，需要对滚刀齿面进行修形，如图1(a)及图1(b)所示，其中1和2为滚刀的齿面修形参数，n为法向压力角，n为法向模数；根据齿条展成渐开线齿面原理(见图1(c))，展成滚刀及大齿轮齿面表示为：

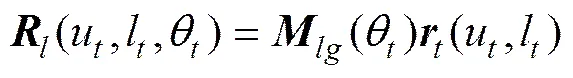
(2)

(a) 法向齿条齿廓修形(滚刀)；(b) 法向齿条齿向修形(滚刀)；(c) 齿条法向廓形(大齿轮)；(d) 齿条展成齿轮坐标系

图1 齿条展成滚刀及大齿轮齿面

Fig. 1 Coordinate systems of modified rack-cutter and generating helical gear

式中：和分别为位矢和法矢，下标为和，分别表示滚刀及大齿轮；为法向齿条位矢，下标为和，分别表示展成滚刀及大齿轮分析齿条；u和l分别为齿条参数；r为节圆半径；θ为展成角。

2 切向滚齿数学模型

滚齿加工近似于1对相错轴渐开线圆柱齿轮传动，滚刀螺旋角与工件的螺旋角形成1个轴交角，径向中心距为0(如图2(a)所示)；h和2分别为滚刀、工件动坐标系；a，b，c和d分别为参考坐标系；滚齿过程中主要有3个运动：滚刀绕自身轴的转动，转角为1；滚刀沿工件轴向进给，位移为l；滚刀沿工件切向进给，进给位移为l；工件绕自身轴转动，转角为2。安装参数和0表示为：

(5)

切向滚齿过程中切向速度通常为轴向速度的线性函数即

切向滚齿时，由于滚刀的轴向进给及切向进给，工件需要有附加转角，工件转角为

(7)

式中：1和2分别为滚刀及小轮(工件)螺旋角，与旋向有关系，同向取正，反向取负；1和2分别为滚刀及小轮齿数(头数)；3为滚刀切向运动系数；1和2分别为工件和滚刀的节圆半径。

根据式(6)和(7)切向滚齿可以简化为2自由度滚齿，该过程中l与1为独立的运动参数，二者之间没有函数关系，根据空间齿面啮合原理，将滚刀齿面位矢从坐标系h变换到工件坐标系2中，同时在l和s取某个值时，均应满足啮合方程式，因此，工件齿面位矢及法矢为：

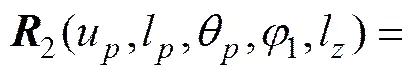
(8)

(9)

(11)

式中：1a，ab，bc，cd和dh为从滚刀到工件的坐标变换矩阵；1a，ab，bc，cd和dh为其相应3×3子矩阵。

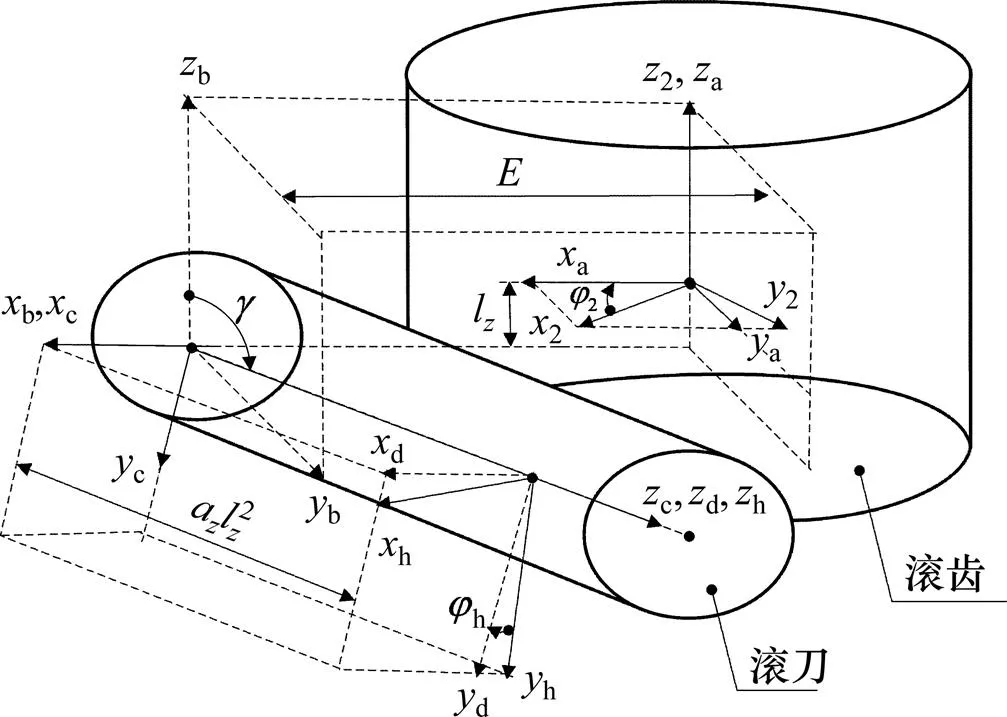
图2 切向滚齿坐标系

3 工件齿面修形量计算

通过修形滚刀齿形及改变工件转角及中心距可实现齿向的修形，即

(13)

将齿面划分为9×15个网格，对比滚齿面与标准渐开线齿面，网格，处的修形量表示为

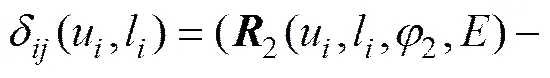
(14)

4 优化LTE幅值计算滚齿加工参数

4.1 齿面接触分析

通过齿条展成滚刀齿面及大轮齿面(标准渐开线齿面)，再通过滚刀齿面进行2自由度切向滚齿得到小轮修形齿面，小轮轮齿面参数为u，l，θ，1和l，大轮轮齿面参数为u，l和θ。图3所示为齿轮副安装坐标系，其中，1和2分别为小轮、大轮运动坐标系，h1，h2和f为参考坐标系，，Δ为安装中心距及误差，Δ为轴交角安装误差，和分别为小轮、大轮转角，TCA方程表达式为：

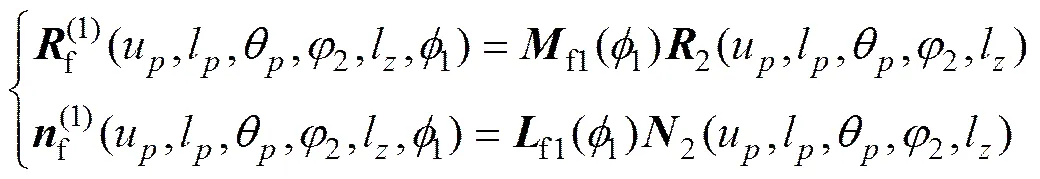
(16)

(17)

式中：f1，f2，f1和f2分别为齿面动坐标系到固定坐标系的转化矩阵。

式(17)中，变量为u，l，θ，2，s，u，l，θ，和，共计10个，取为输入量，则变量为9个，需要9个方程可确定唯一解。式(17)可分解为5个方程式，加上4个啮合方程式，即式(3)为齿条展成大轮、滚刀齿刀齿面啮合方程(共计2个)，式(10)~(11)为滚刀包络小轮齿面啮合方程，可确定唯一解。通过TCA得到UTE为

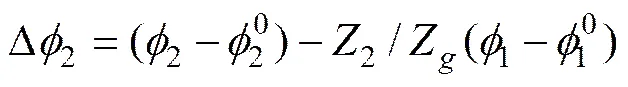
图3 TCA安装坐标系

Fig. 3 Coordinate system applied for TCA

4.2 优化模型

本文的LTCA方法[22]是一种在TCA基础上，将有限元法与几何计算结合起来，考虑多齿对接触，将齿轮副受力接触转化为求解齿面有限个离散接触点的力学平衡问题，通过复合形方法求解非线性方程组得到加载后齿轮副瞬时接触线上离散点的载荷和一个啮合周期法向变形，将该法向变形Z转化为啮合线上的位移，用转角(单位：(″))形式表示，即一个啮合周期的LTE为

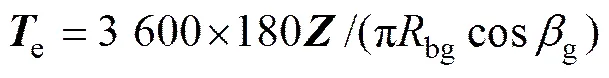
式中：bg和g分别为被动大轮基圆半径和螺旋角。

通过优化一个啮合周期的LTE幅值最小确定修形系数s,s,s，目标函数表示为

优化过程即通过改变滚刀齿面修形参数及机床运动参数，即优化变量为=[1,2,3,4,5,6,7], 改变小轮齿面修形量，进而改变齿轮副的接触间隙，进行TCA和LTCA的一个非线性迭代过程，优化变量与优化目标函数之间没有直接联系，在实际中不能建立由优化变量到目标函数的解析表达式，而且在优化解空间内存在多个局部最优解，因此，传统的优化算法在此并不适用；粒子群算法且具有全局收敛性，可以求解具有多个局部极值的非线性优化问题，结构简单，因此本文应用该优化算法求解，其流程如图4所示。

图4 修形参数优化流程图

Fig. 4 Flowchart of modification parameters optimization

5 算例与分析

以文献[9]中滚刀、斜齿轮副参数为例(见表1)，负载扭矩500 N∙m工况为优化目标，其中展成滚刀的齿条齿廓进行4次抛物线修形，齿向进行2次抛物线修形。当滚刀有齿向修形时，工件齿向扭曲程度受滚刀切向进给速度影响，因此，本文给定滚刀齿向修形系数即2=−1×10−8，主要优化滚刀齿廓修形参数1、滚齿切向进给速度参数3、滚齿中心距参数4、滚齿工件附加转角参数5~7共计6个。优化结果见表2，最佳修形齿面(图5)。分析如下：1) 仅修形滚刀齿形后，将对工件产生齿形修形(图6(a))；对滚刀进行齿向修形后，切向速度将影响齿形扭曲程度；当切向运动系数7=3.2时，齿向无扭曲现象(图6(b)~(d))。需要说明的是：扭曲程度与滚刀齿向修形量或滚刀长度有关；改变中心距将导致工件齿形扭曲(图6(e))；修正工件附加转角导致工件齿形扭曲(图6(f)~(h))。可见：当滚刀沿齿向修形量或当齿向修形量一定时，滚刀长度或切向进给速度及滚切中心距变化对工件齿形扭曲程度有重要影响；通过对滚刀沿齿向进行齿形修形后，再增加切向运动，使得滚切过程中产生沿齿向方向齿形的连续变化，弥补了传统加工(改变中心距)由于滚刀齿形无变化而产生的扭曲。2) 修形齿面载荷分布均匀，载荷主要分布在齿面中部，无边缘接触，有安装误差时，载荷略向端部移动(图7(a)~(d)，图8(a)~(d))，修形降低了齿轮副的安装误差敏感性；3)无修形时，1个啮合周期呈现双齿、三齿交替啮合，双齿啮合区变形大于三齿啮合区变形(见图9(a))，由于重合度不变，因此，随载荷增加，双齿较三齿啮合区变形逐渐增大；修形后随载荷增大，呈现单、双齿交替啮合且重合度不断增大(0~400 N∙m)，双、三齿交替啮合且重合度不断增加(400~700 N∙m)及不变(≥700 N∙m) 3个状态(图9(b))，因此，会在承载传动误差幅值曲线上有3个变化，但是，由于齿面有齿向修形，即接触线上法向间隙影响重合度变化，这3段变化在承载传动误差曲线上不是很明显(图9(c))。

表1 滚齿基本参数

表2 优化的修形参数

图5 优化齿面拓扑修形量

(a) a1=−1×10−2, a2=0, a3=−2.2, a4=0, a5=0, a6=0, a7=0; (b) a1=0, a2=−1×10−7,a3=−2.2, a4=0, a5=0, a6=0, a7=0; (c) a1=0, a2=−1×10−7, a3=−3.2, a4=0, a5=0, a6=0, a7=0; (d) a1=0, a2=−1×10−7, a3=−4.2, a4=0, a5=0, a6=0, a7=0; (e) a1=0, a2=0,a7=−2.2, a4=0.001, a5=0, a6=0, a7=0; (f)a1=0, a2=0, a3=−2.2, a4=0, a5=1×10−6, a6=0, a7=0; (g) a1=0, a2=0, a3=−2.2, a4=0, a5=0, a6=1×10−6, a7=0; (h) a1=0, a2=0, a3=−2.2, a4=0, a5=0, a6=0, a7=1×10−6

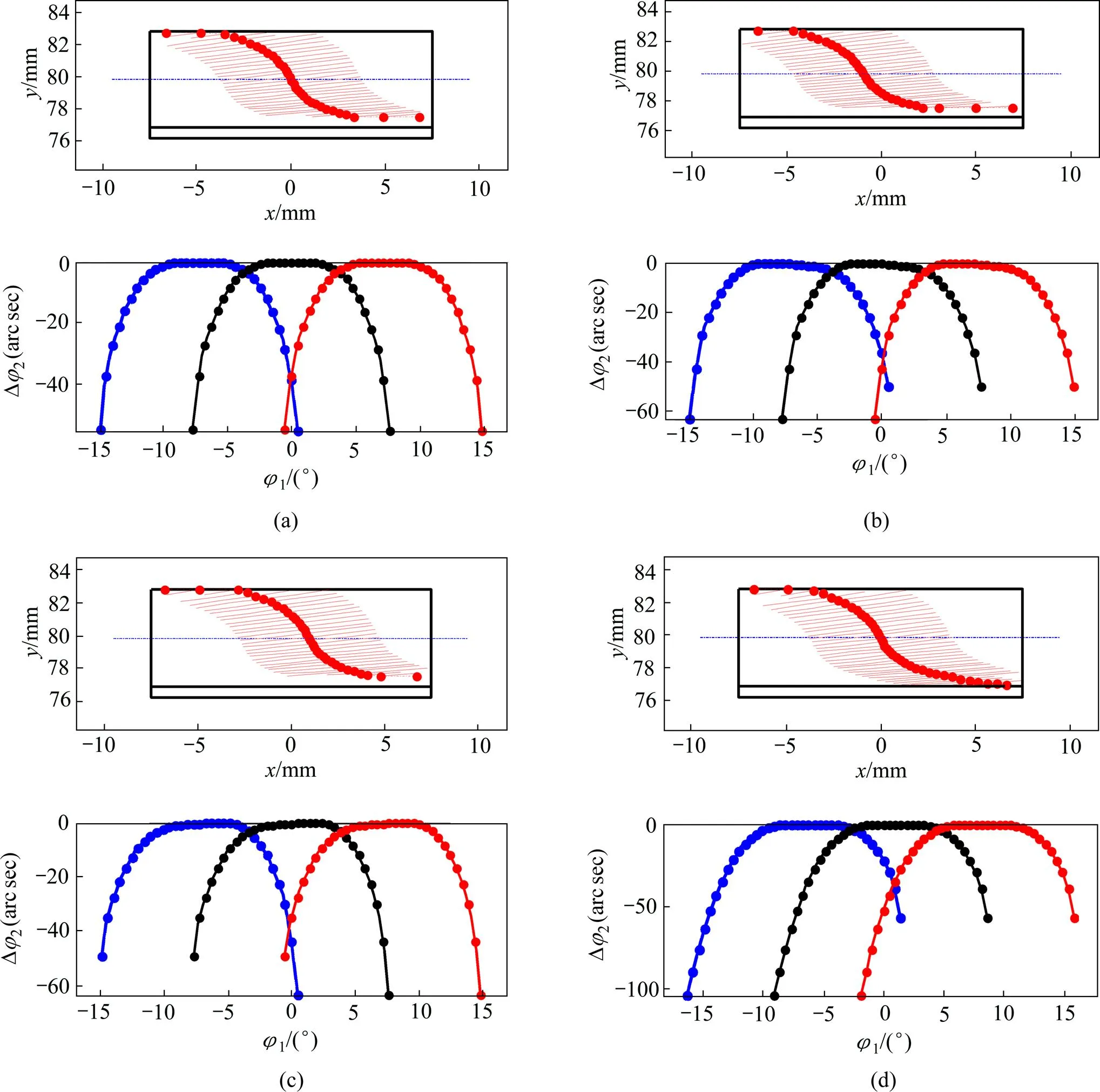
(a) Δγ=0; (b) Δγv=5′; (c) Δγh=5′; (d) ΔE=−1 mm

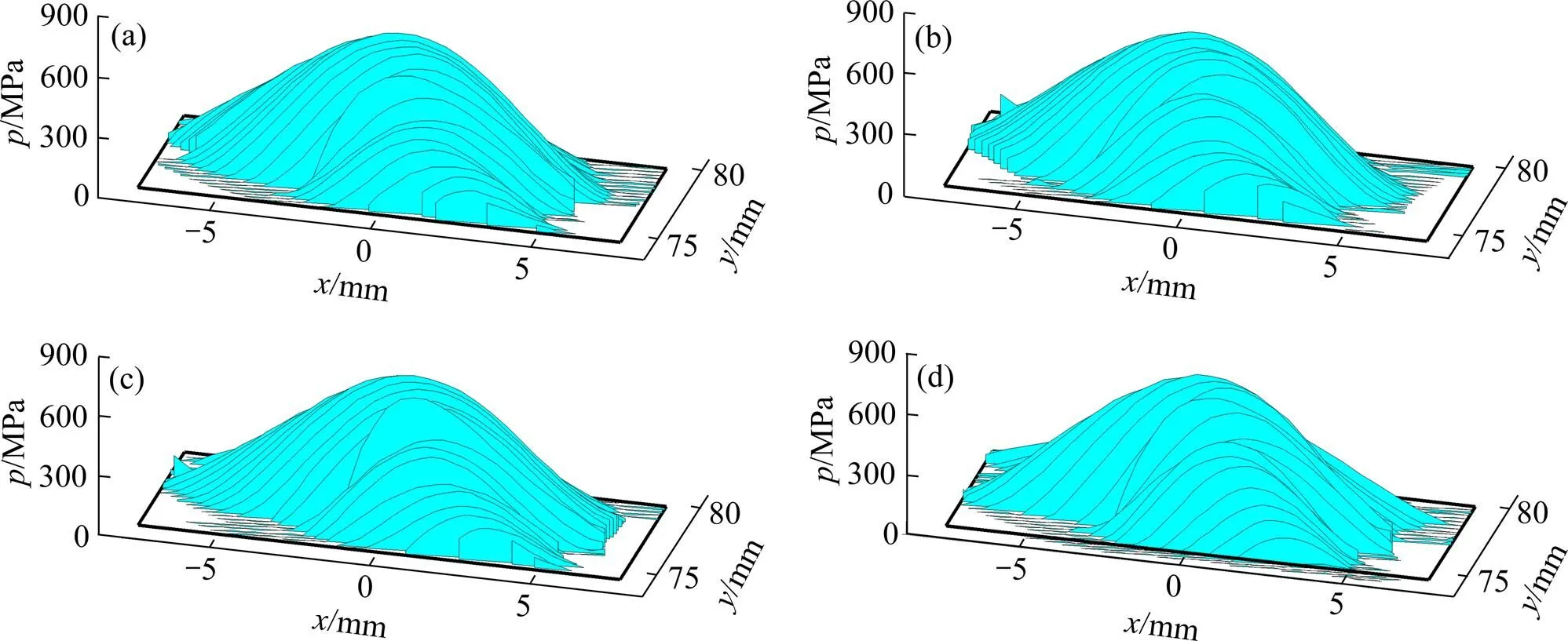
(a) Δγ=0; (b) Δγv=5′; (c) Δγh=5′; (d) ΔE=−1 mm

(a) 多载荷承载传动误差(无修形)；(b) 多载荷承载传动误差(拓扑修形)；(c) 多载荷承载传动误差幅值

6 结论

1) 根据空间啮合原理，建立了3自由度切向滚齿模型，设计了滚刀齿面抛物线修形参数及运动修形参数，求解了工件拓扑修形齿面。

2) 结合LTCA技术以LTE幅值最小，获得滚刀齿面修形参数及运动参数。结果表明：该拓扑修形齿轮可减小安装误差敏感性，避免边缘接触，降低齿轮副LTE幅值，减小振动与噪音。

3) 当滚刀有齿向修形时，合理的切向进给速度可避免工件齿形扭曲。

4) 无修形齿轮由于重合度不变，因此，随载荷增加，LTE幅值不断增加；修形后随载荷增加，齿面间隙逐渐压实重合度不断增加，因此，LTE幅值逐渐降低；当齿面间隙完全压实后，重合度不再变化，随载荷增加，传动误差逐渐增大。

参考文献：

[1] CHIU H, UMEZAKIY Y, ARIURA Y. An improvement of the tooth profile accuracy of a hobbed gear by adjusting the hob eccentricity[J]. JSME International Journal: Ser. 3. Vibration, Control Engineering, Engineering for Industry, 1989, 32(1): 131−135.

[2] NAGATA S A General mathematical model for gears cut by GNC mobbing machines[J]. Journal of Mechanical Design, 1997, 119(1): 108−113.

[3] BOUZAKIS K D, ANTONIADIS A. Optimizing of tangential tool shift in gear hobbing[J]. CIRP Annals Manufacturing Technology, 1995, 44(1): 75−78.

[4] BOUZAKIS K D, KOMBOGIANNIS S, ANTONIADIS A, et al. Gear hobbing cutting process simulation and tool wear prediction models[J]. Journal of Manufacturing Science and Engineering, 2002, 124(1): 42−51.

[5] VEDMAR L. A parametric analysis of the gear surface roughness after hobbing[J]. Journal of Mechanical Design, 2010, 132(11): 111004-1−111004-8.

[6] INNOCENTI C. Optimal choice of the shaft angle for involute gear hobbing[J]. Journal of Mechanical Design, 2008, 130(4): 044502-1−044502-5.

[7] XIA L, LIU Y, LI D, et al. A linkage model and applications of hobbing non-circular helical gears with axial shift of hob[J]. Mechanism and Machine Theory, 2013, 70: 32−44.

[8] HSU R H, SU H H. Tooth contact analysis for helical gear pairs generated by a modified hob with variable tooth thickness[J]. Mechanism and Machine Theory, 2014, 71: 40−51.

[9] HSU R H, TSAY C B. Study on the anti-twist helical gear tooth flank with longitudinal tooth crowning[J]. Journal of Mechanical Design, 2014, 136(6): 061007-1−061007-10.

[10] HSU R H, FONG Z H. Novel variable-tooth-thickness hob for longitudinal crowning in the gear-hobbing process[J]. Mechanism and Machine Theory, 2011, 46(8): 1084−1096.

[11] RADZEVICH S P. About hob idle distance in gear hobbing operation[J]. Journal of Mechanical Design, 2002, 124(4): 772−786.

[12] RADZEVICH S P. A way to improve the accuracy of hobbed involute gears[J]. Journal of Mechanical Design, 2007, 129(10): 1076−1085.

[13] RADZEVICH S P. Investigation of the tooth geometry of a hob for machining of involute gears (in the tool-in-use reference system)[J]. Journal of Manufacturing Science and Engineering, 2007, 129(4): 750−759.

[14] RADZEVICH S P. A novel design of cylindrical hob for machining of precision involute gears[J]. Journal of Mechanical Design, 2007, 129(3): 334−345.

[15] SHIH Y P, CHEN S D. A Flank correction methodology for hob sharpening on the five-axis CNC hob sharpening machine[J]. Computer-Aided Design and Applications, 2012, 9(4): 585−598.

[16] CHENG Y, LIM T C. Dynamics of hypoid gear transmission with nonlinear time-varying mesh characteristics[J]. Journal of Mechanical Design, 2003, 125(2): 373−382.

[17] WANG J, LIM T C, LI M. Dynamics of a hypoid gear pair considering the effects of time-varying mesh parameters and backlash nonlinearity[J]. Journal of Sound and Vibration, 2007, 308(1): 302−329.

[18] WANG P Y, FONG Z H. Fourth-order kinematic synthesis for face-milling spiral bevel gears with modified radial motion (MRM) correction[J]. Journal of Mechanical Design, 2006, 128(2): 457−467.

[19] SIMON V V. Design and manufacture of spiral bevel gears with reduced transmission errors[J]. Journal of Mechanical Design, 2009, 131(4): 041007-1−041007-11.

[20] SIMON V V. Loaded tooth contact analysis and stresses in spiral bevel gears[C]//ASME 2009 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference. American Society of Mechanical Engineers, 2009: 271−279.

[21] ARTONI A, KOLIVAND M, KAHRAMAN A. An ease-off based optimization of the loaded transmission error of hypoid gears[J]. Journal of Mechanical Design, 2010, 132(1): 011010.

[22] ZHANG Y, FANG Z. Analysis of transmission errors under load of helical gears with modified tooth surfaces[J]. J Mech Des, 1997, 119(3): 120−126.

(编辑 陈爱华)

Design and analysis for topologically modified helical gear finished by gear-hobbing

JIANG Jinke, FANG Zongde

(School of Mechanical Engineering, Northwestern Polytechnical University,Xi’an 710072, China)

A design and an analysis of topologically modified helical gears were proposed to improve the machining efficiency and reduce the noise and vibration. Firstly, the topologically modified pinion tooth surfaces finished by hobbing was established according to the meshing theory of three independent motion parameters of the tight rational meshing between work-gear and hobbing cutter and the traverse motion of work-gear along the axis of the work gear and tangential feed along the axis of the hobber. Besides, the modified teeth were determined by the profile gear-hob, the center distance between work-gear and hobbing cutter, the hob tangential feed and additional rotation angle of work gear. Secondly, the parameters were individually determined based on TCA and LTCA by optimizing the aim of minimum the amplitude of loaded transmission error of drive gears. Finally, a numerical simulation of example was performed. The characteristics of amplitude of LTE curves were investigated by analyzing the contact ratio with increasing loads on modified gears. The results show that the optimal modified tooth surfaces can reduce sensitivity caused by errors of axes alignment and prevent the gear’s meshing teeth from colliding with each other at the boundary, and make lower amplitude of LTEs reduce by 44%, which contributes to a lower vibration and noise. Besides, an accurate tangential feed of the hob with longitudinal correction can attain an anti-twist helical gear tooth flank with longitudinal tooth crowning, because continuous changes in profile along longitudinal of hobber contribute to reducing distortion of profile due to variable center distance hobbing without compensation of profile.

gear-hobbing; topological modification; TCA; LTCA; loaded transmission error

10.11817/j.issn.1672-7207.2016.11.009

TH133

A

1672−7207(2016)11−3677−08

2016−01−11；

2016−04−25

国家自然科学基金资助项目(51175423, 51375384) (Projects(51175423, 51375384) supported by the National Natural Science Foundation of China)

方宗德，教授，博士生导师，从事齿轮啮合理论、齿面设计及汽车动力学等研究；E-mail: fauto@ nwpu.edu.cn