考虑抗剪强度参数空间变异性的边坡稳定性分析

袁葳，常晓林，段寅, 3，程勇刚，马刚



考虑抗剪强度参数空间变异性的边坡稳定性分析

袁葳1, 2，常晓林1，段寅1, 3，程勇刚1，马刚1

(1. 武汉大学水资源与水电工程科学国家重点实验室，湖北武汉，430072；2. 湖北省水利水电规划勘测设计院，湖北武汉，430064；3.长江勘测规划设计研究院，湖北武汉，430010)

提出基于商业软件ABAQUS的边坡稳定分析的随机有限元法。采用Karhunen-Loeve级数展开方法建立土体抗剪强度参数的随机场模型，在强度折减有限元法的基础上模拟边坡失稳过程，并采用塑性屈服区贯通以及计算不收敛判据作为边坡失稳判据，利用python脚本文件分析最危险滑面分布规律。运用该方法研究土体内摩擦角和黏聚力的空间变异性对边坡稳定性的影响。研究结果表明：所提的边坡稳定分析的随机有限元法操作简单易于实现，能够从安全系数以及最危险滑面2个方面分析土体抗剪强度参数的空间变异性对边坡稳定性的影响；内摩擦角随机场中相关长度的改变对边坡的稳定性影响不明显；而黏聚力的空间变异性对边坡稳定性影响则相对更大，黏聚力随机场中水平与竖直相关长度的比值不同，边坡稳定性的变化规律不同。此外，内摩擦角与黏聚力的相关系数越大，失效概率越高，最危险滑面分布越广。

空间变异性；边坡稳定性；强度折减有限元法；随机有限元方法

在岩体工程领域，传统的考虑边坡稳定性的方法是使用安全系数评判其风险等级。但是，安全系数并非评判边坡风险等级的唯一标准，即使边坡具有相同的安全系数，由于土体参数的不均匀性，其风险等级可能是不同的[1]。因此，近年来众多学者系统地研究了边坡的可靠度分析方法。GRIFFITH等[2−3]提出了基于强度折减法和随机场理论的随机有限元方法，对比了采用随机变量模型和随机场模型分析边坡可靠度的成果。SHEN等[4]结合弹塑性有限差分法和随机场理论分析非均质边坡的可靠度，采用局部平均法模拟黏聚力参数的空间变异性。CHO[5]运用随机极限平衡法研究土体抗剪强度的空间变异性对边坡稳定性的影响，采用Karhunen-Loeve级数展开方法模拟土体参数的空间变异性。谭晓慧等[6]基于一阶可靠度方法，对边坡的整体可靠度指标进行了计算。吴振君等[7]采用验算点法和一维随机场模拟实现了考虑地质成因的土坡可靠度分析。李典庆等[8−11]提出了非侵入式随机有限元方法，研究了该方法在边坡稳定、地下洞室可靠度分析中的应用。国内外学者进行边坡可靠度分析时多采用传统极限平衡法(LEM)[1, 5−6]，LEM方法计算时间短，适用于蒙特卡洛模拟，但是，采用LEM计算时需要假定临界滑面，通常基于特定的滑面计算边坡失效概率。与LEM相比，弹塑性有限元分析方法无需假定临界滑面的位置，能够求得任意形状的滑面及相应的折减系数，更为真实地反映边坡的稳定性。GRIFFITH等[2−3]针对随机有限元方法进行了大量的研究，采用局部平均法模拟参数空间变异性，依据迭代不收敛判据得到边坡的安全系数。然而，采用局部平均法时，随机变量的数目与有限元单位的数目相同，计算效率不高。肖特等[12]提出基于有限元强度折减法的非侵入式边坡可靠度分析方法，采用位移突变作为边坡失稳的判据，应用于多层土质边坡可靠度分析。上述基于弹塑性有限元法的边坡可靠度研究往往局限于安全系数、失效概率等指标的规律，针对滑面的分布规律的研究偏少，然而，潜在的滑坡的规模与边坡最危险滑面的分布直接相关。因此，有必要从边坡安全系数与最危险滑面分布2方面研究岩土参数空间变异性对边坡稳定性的影响。本文作者提出了基于有限元软件ABAQUS的边坡稳定分析的随机有限元法。该方法采用Karhunen-Loeve级数展开方法建立土体参数的随机场模型；基于强度折减有限元法模拟边坡失稳过程；主要以塑性屈服区贯通作为边坡失稳判据；利用python脚本文件对计算结果进行后处理以得出最危险滑面分布规律。然后，在蒙特卡洛随机有限元法的基础上，从安全系数和最危险滑面分布2个方面，研究了土体内摩擦角和黏聚力的空间变异性对边坡稳定性的影响。

1 土体空间变异性的随机场模拟

1.1 Karhunen-Loeve级数展开方法

采用Karhunen-Loeve级数展开方法离散随机场实质上将土体参数随机场的离散转化为求解第2类Fredhom积分方程的特征值问题，即

式中：1和2为随机场区域内任意两点的坐标；为随机场区域内任意两点的特性值之间的相关函数值；和分别为与相关函数对应的特征值以及特征函数。

根据求解Fredhom积分方程的方法的不同，K-L级数展开方法可以分为解析法和数值法。解析方法在具体工程应用中具有局限性，部分随机场的相关函数的特征值以及特征函数用解析方法求解困难，甚至不可解。LI等[1]研究了不同相关函数对边坡可靠度指标的影响，研究表明影响不大。因此，本文采用的相关函数为指数型式，并采用解析方法求解Fredhom积分方程，以减小程序的复杂性。指数型相关函数如下：

式中：和为随机场区域内任意点的坐标；h和v分别为水平向和竖直向相关长度。

当相关函数是可分离时，二维随机场相关函数的特征值可简化为一维相关函数特征值的乘积。以一维标准高斯随机场为例，详细说明K-L级数展开方法的具体过程。假定，特征值和特征函数满足第2类Fredhom积分公式：

其中相关函数为

(4)

将式(4)代入式(3)得

(6)

由式(6)解得

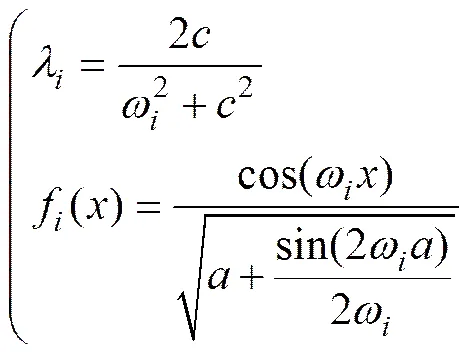
当为偶数时，由式(5)可得

(8)

由式(8)解得

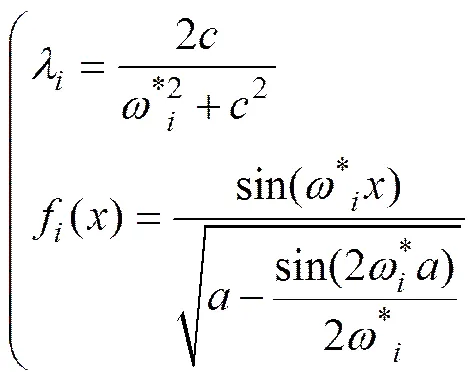
基于以上计算过程得到的相关函数的特征解，可将标准高斯随机场展开为

(10)

本文假定土体的内摩擦角和黏聚力服从Weibull分布，其概率密度函数、累积分布函数、均值、标准差分别为：

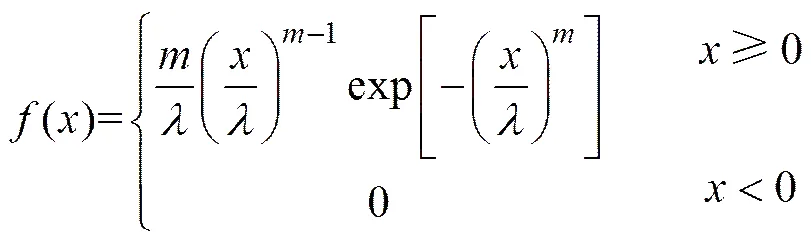
(12)

(13)

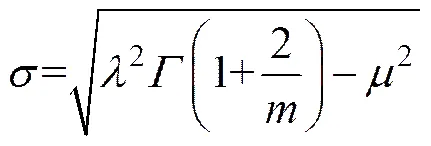
式中：为均质度，越大，参数分布越均匀。

将土体参数在计算区域内模拟为二维Weibull分布的统计均质随机场，通过等概率变换，Weibull随机场可以表示为

在计算精度满足要求的前提下，通常截取前项K-L级数展开以提高计算效率，式(15)截取前项后可表示为

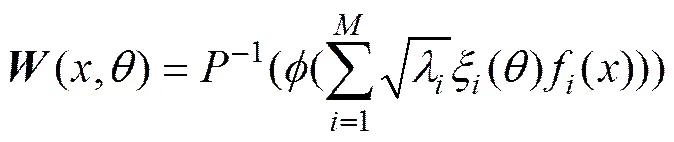
1.2 抗剪强度参数随机场的模拟

本文模拟土体参数的随机分布分为3种：1) 考虑内摩擦角的空间变异性；2) 考虑黏聚力的空间变异性；3)同时考虑两者的空间变异性。以上3种情况均采用Weibull随机场表征参数的空间变异性。随机场的模拟采用1.1节介绍的K-L级数展开方法。边坡的几何尺寸以及有限元网格见3.1节。

图1所示为土体内摩擦角随机场在2种均质度下的模拟结果，内摩擦角的均值均为15°。由图1可以看出：当=2时，内摩擦角取值分散；而当=5时，内摩擦角取值集中。

(a) mφ=2, lφ,h=20 m, lφ,v=2 m; (b) mφ=5, lφ,h=20 m, lφ,v=2 m

图2所示为土体黏聚力随机场在4种不同水平向和竖直向相关长度组合下的模拟结果，黏聚力的均值均为20 kPa。在均质度相同的情况下，当时，黏聚力随机场中高黏聚力带和低黏聚力带呈水平向层状分布；当时，呈块状分布；相关长度越长，高黏聚力带、低黏聚力带越连续。

模拟具有一定相关性的内摩擦角和黏聚力随机场时，通过控制随机向量和之间的相关性进而得到具有相同相关性的内摩擦角和黏聚力随机场。图3给出了土体内摩擦角、黏聚力随机场在2种不同相关系数下的模拟结果。其中内摩擦角和黏聚力均服从=3的Weibull分布，均值分别为15°和20 kPa，水平相关长度取20 m，竖直相关长度取2 m。当时，内摩擦角随机场与黏聚力随机场分布规律大致相反，即内摩擦角大的区域其黏聚力较低；当时，内摩擦角随机场与黏聚力随机场分布规律相似。

(a) mc=3, lc,h=2 m, lc,v=2 m; (b) mc=3, lc,h=20 m, lc,v=20 m; (c) mc=3, lc,h=10 m, lc,v=1 m; (d) mc=3, lc,h=40 m, lc,v=4 m

(a), (b) r(c,φ)=−0.5; (c), (d) r(c,φ)=0.5

2 边坡强度折减有限元法

ZIENKIEWICS等[13]于1975年提出强度折减有限元法，经过几十年的发展，强度折减有限元法在边坡稳定分析方面取得了众多成果，GRIFFITH等[14]运用强度折减非线性有限元法对不同类型的边坡进行了研究，验证了该方法的可靠性；DAWSON等[15]讨论了网格密度、单元类型、边界范围、屈服准则等对计算精度的影响；栾茂田等[16]、刘金龙等[17]、吕庆等[18]对边坡失稳判据进行了研究。边坡失稳判据通常分为3类：计算不收敛、塑性屈服区贯通以及特征点位移突变。考虑到边坡中不同特征点的位移曲线存在一定的差异，且曲线的突变点不易确定，本文主要采用计算不收敛判据以及塑性屈服区贯通判据。

本文依托有限元软件ABAQUS，利用其用户子程序接口USDFLD实现场变量与时间步长、材料参数的对应关系，在每个分析步中，材料强度参数在给定的范围内逐渐折减，利用ABAQUS/Standard模块模拟边坡破坏过程。

图4给出了编写的用户子程序USDFLD的主要计算流程，其中表示计算时间，NOEL表示单元编号，K表示时刻对应的折减系数。单元的初始强度参数符合Weibull分布，实现Weibull随机场的程序嵌入USDFLD用户子程序中，仅在总时间为0时被调用。本文通过2个(0,1)内均匀分布的独立随机数转换得到标准正态随机数，其中均匀分布随机数是由fortran自带的函数random_number生成。

图4 用户子程序USDFLD计算流程

3 边坡稳定的确定性分析

3.1 计算模型

本文采用的算例为一均质土坡，尺寸如图5所示，坡高为10 m，坡比为1:2。计算参数如下：黏聚力20 kPa，内摩擦角15°，重度20 kN/m3，弹性模量8 MPa，泊松比0.25。

在ABAQUS中按照平面应变问题建立二维边坡有限元分析模型，如图6所示，共剖分1 200个单元和1 281个节点。土体采用理想弹塑性本构模型和Mohr-Coulomb屈服准则。计算时模型底部采取固定约束，两侧采取法向约束；模型施加自重荷载。

图5 边坡几何尺寸

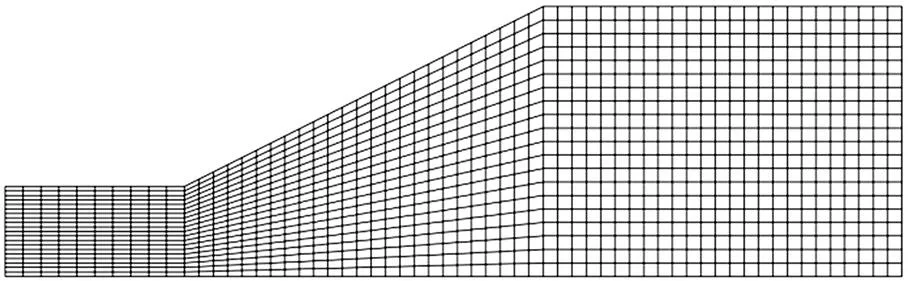
图6 边坡有限元模型

3.2 确定性分析

本节计算未考虑参数的空间变异性，每个单元赋予相同的和。计算时设定的强度折减系数的变化范围为0至5.0，每一个分析步内S增加0.1。图7所示为边坡S=1.54和1.55时的等效塑性应变云图，从图7可以看出：当S=1.54时，坡脚开始出现塑性屈服区，随着的增加，塑性屈服区逐渐向坡顶扩展；当S=1.55时，塑性屈服区完全贯通，形成了从坡顶至坡脚的连续滑动面；当折减系数为1.77时，计算不收敛。

(a) FS=1.540; (b) FS=1.550

为了对比分析强度折减有限元法和传统极限平衡法的计算结果，本文采用加拿大边坡分析软件SLOPE/W按照Morgenstern-Price法计算得到的该边坡的安全系数为1.533。确定性分析时，根据计算不收敛得到的边坡安全系数大于依据塑性区贯通判据得到的安全系数，且后者得到的安全系数与极限平衡法计算得到的安全系数十分接近，相对误差仅为1.11%，二者计算得到的滑面位置基本一致。因此，本文确定边坡安全系数时以塑性屈服区贯通判据为主，以计算不收敛判据为辅。

4 边坡稳定的随机分析

进行随机分析时，计算结果数量大，重复性工作多，为了高效地判断边坡的安全系数以及确定最危险滑面的位置，编写python脚本对结果文件进行后处理，以得出最危险滑面分布规律。本文确定最危险滑面的方法与文献[19]中所描述的方法类似，即将水平坐标相同的单元分为一组，提取每组中等效塑性应变最大的单元的形心坐标，当计算到某一步时，提取的所有单元形心能够连成完整的滑面，此时对应的折减系数即为边坡的安全系数，所连的滑面即为最危险滑面。以第3节确定性计算结果为例验证所提后处理方法的可行性，运行python脚本文件，可得塑性屈服区贯通时对应的安全系数为1.55，计算不收敛时对应的安全系数为1.77，最危险滑面如图8所示，与图7(b)中贯通的等效塑性应变带位置一致。

图8 最危险滑面

为了更全面地分析抗剪强度参数的空间变异性对边坡稳定的影响，定义失效概率为

式中：f为安全系数小于1.0的次数；m为总共的随机次数。

4.1 内摩擦角的空间变异性的影响

本节计算只考虑内摩擦角的空间变异性，计算模型与确定性分析中采用的模型一致，计算参数见表1，黏聚力均取20 kPa。2组试验分别考虑均质度和相关长度对边坡稳定性的影响。通常水平方向相关长度大于竖直方向相关长度[20]，故考虑均质度对边坡稳定性的影响时，取,h=20 m，,v=2 m。

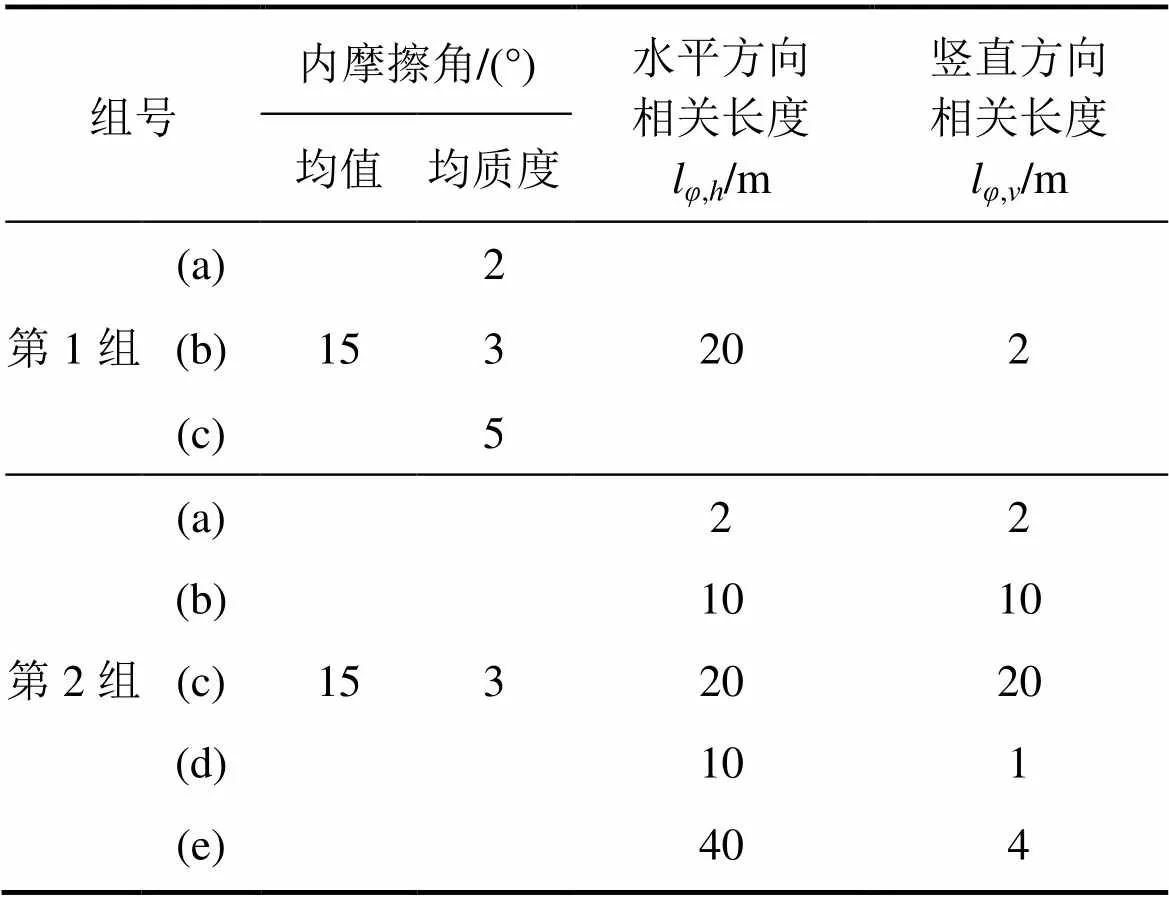
表1 考虑内摩擦角空间变异性时的参数

图9所示为内摩擦角=3，,h=20 m，,v=2 m对应的随机分析结果。当随机次数达到200以上时，平均安全系数呈降低的趋势；边坡失效概率持续为0，考虑到计算时间和计算精度，每组计算时随机次数为200次。

图9 蒙特卡洛随机分析结果(mφ=3，lφ,h=20 m，lφ,v=2 m)

表2所示为内摩擦角随机场在不同均质度下边坡安全系数的统计参数。随着均质度的增加，平均安全系数由1.39提高到1.51，变异系数、失效概率降低。图10所示为不同均质度下最危险滑面分布范围。对比=2和=5时滑面分布可以看出，均质度越高，最危险滑面分布越集中。

表2 考虑内摩擦角，lφ,h=20 m，lφ,v=2 m时不同均质度对应的安全系数分布

图10 考虑内摩擦角，lφ,h=20 m，lφ,v=2 m时不同均质度对应的最危险滑面分布

表3所示为内摩擦角随着机场在不同相关长度下边坡安全系数的统计参数。图11所示为不同相关长度下最危险滑面分布范围。当,h/,v=1时，随着相关长度的增加，平均安全系数仅提高2%，变异系数提高，失效概率不超过0.01；最危险滑面分布更加集中。当,h/,v=10时，变异系数和失效概率的变化规律与,h/,v=1时一致，平均安全系数稍微降低；最危险滑面分布范围扩大。

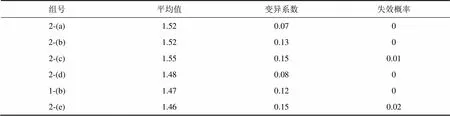
表3 考虑内摩擦角，mφ=3时不同相关长度对应的安全系数分布

(a) lφ,h/lφ,v=1; (b) lφ,h/lφ,v=10

对比内摩擦角随机场在不同均质度与不同相关长度下的计算结果可知，边坡的整体稳定性对于内摩擦角均质度的敏感性高于相关长度，均质度越高，平均安全系数与确定性计算结果越接近；相关长度的改变对边坡的平均安全系数和失效概率影响不大。

4.2 黏聚力的空间变异性的影响

本节计算只考虑黏聚力的空间变异性，计算模型与确定性分析中采用的模型一致，计算参数见表4，内摩擦角均取15°。

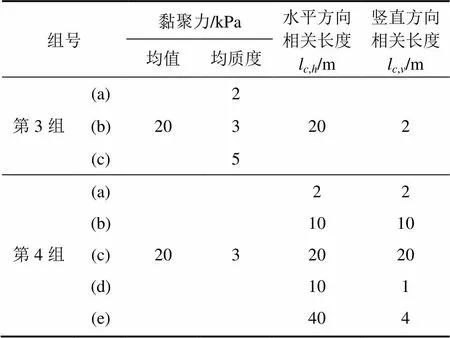
表4 考虑黏聚力空间变异性时的参数取值

图12所示为黏聚力=3，,h=20 m，,v=2 m对应的随机分析结果。由图12可知：当随机次数超过200次时，曲线趋于平缓，故本节每组计算时随机次数定为200次。

(a) 平均安全系数；(b) 失效概率

表5所示为黏聚力随机场在不同均质度下边坡安全系数的统计参数，平均安全系数、变异系数、失效概率的变化规律与考虑内摩擦角的均质度变化时得出的规律相同，但是变化幅度明显提高，当=2时，平均安全系数为1.10，当=5时，平均安全系数增加到1.49，失效概率由0.40下降到0.01；在相同的均质度下，与内摩擦角的空间变异性相比，黏聚力的空间变异性对边坡稳定性的影响更大，平均安全系数更低，变异系数、失效概率更高。图13所示为不同均质度下最危险滑面分布范围。随着均质度提高，最危险滑面分布逐渐集中。

表5 考虑黏聚力，lc,h=20 m，lc,v=2 m时不同均质度对应的安全系数分布

图13 考虑黏聚力，lc,h=20 m，lc,v=2 m时不同均质度对应的最危险滑面分布

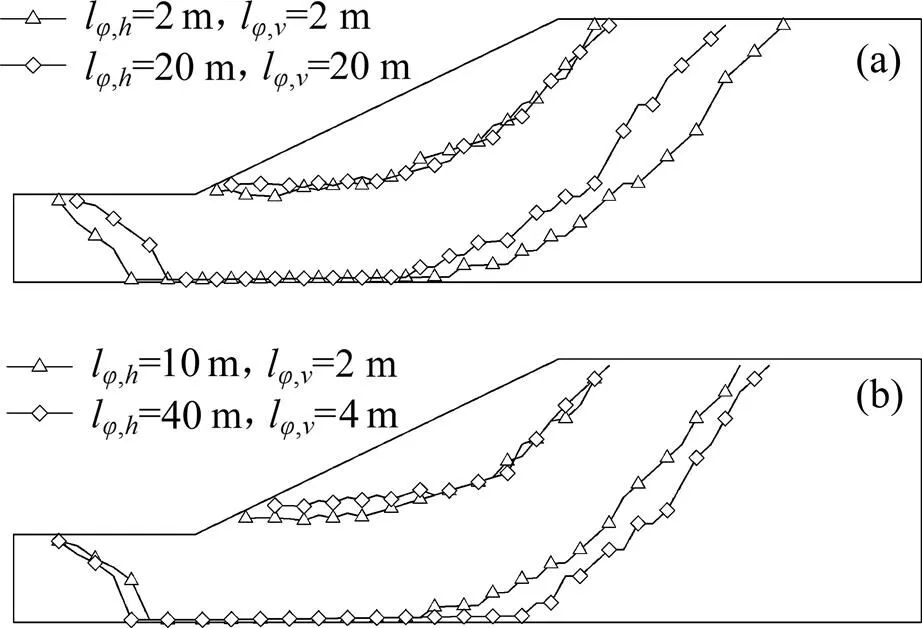
表6所示为黏聚力随机场在不同相关长度下边坡安全系数的统计参数，图14所示为不同相关长度下最危险滑面分布范围。当,h/,v=1时，随着,h由2 m增加到20 m，平均安全系数相应提高，变异系数、失效概率降低，最危险滑面分布范围缩小；而当,h/,v=10时，随着相关长度的增加，平均安全系数等的变化规律与,h/,v=1时相反。

表6 考虑黏聚力，mc=3时不同相关长度对应的安全系数分布

(a) lc,h/lc,v=1; (b) lc,h/lc,v=10

与考虑内摩擦角的空间变异性的计算结果相比，当黏聚力随机场中均质度与相关长度发生变化时，边坡的平均安全系数、变异系数以及失效概率的变化幅度相对较高，可见，黏聚力的空间变异性对边坡稳定性影响大于内摩擦角对其的影响。

黏聚力随机场中水平与竖直相关长度的比值不同，边坡稳定性随着相关长度的改变而变化的规律不同。当,h/,v=1时，水平相关长度趋于无穷大时得到的随机场近似于均质分布的情况，随着,h的增加，平均安全系数趋于确定性计算结果，变异系数、失效概率趋于0，最危险滑面逐渐集中于确定性计算得到的滑面。当,h/,v=10时，,h越长，越易形成连续的低黏聚力区，发生边坡滑动的可能性越高，可能出现的滑面分布范围越广。

4.3 同时考虑两者的空间变异性的影响

本节计算同时考虑了内摩擦角与黏聚力的空间变异性，假定和之间的相关系数分别为−0.5、0以及0.5，计算共分为3组，和均服从=3的Weibull分布，均值分别为20 kPa和15°，水平相关长度取20 m，竖直相关长度取2 m。

表7所示为不同相关系数下边坡安全系数的统计参数，当和由负相关变为正相关时，平均安全系数降低，变异系数、失效概率增加，与文献[5,9]中的规律一致。图16所示为不同相关系数下最危险滑面分布范围，随着相关系数的增加，最危险滑面分布越分散。

(a) 平均安全系数；(b) 失效概率

表7 不同相关系数对应的安全系数分布

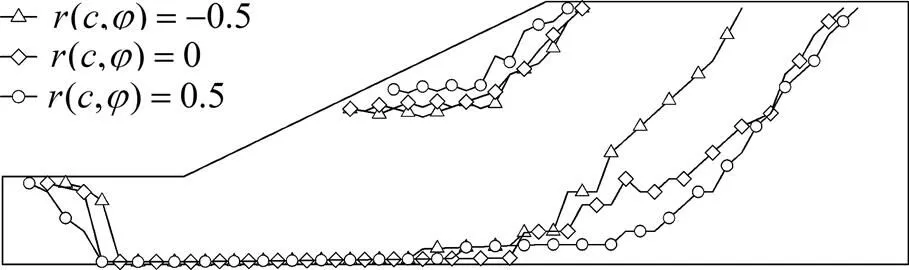
图16 不同相关系数对应的最危险滑面分布

5 结论

1) 所提的随机有限元方法利用ABAQUS提供的用户子程序接口USDFLD编写程序模拟考虑土体抗剪强度参数空间变异性的边坡失稳过程，运用python脚本进行后处理，便于从边坡的安全系数和最危险滑面分布2方面进行边坡稳定性分析，操作简单易于实现，可为复杂边坡的稳定分析提供一条有效的途径。

2) 内摩擦角随机场中均质度越高，边坡越稳定，而相关长度的改变对边坡的稳定性影响不明显；内摩擦角的空间变异性对边坡稳定性的影响小于黏聚力的影响。

3) 黏聚力随机场中水平与竖直相关长度的比值不同，边坡的稳定性随着相关长度的改变而变化的规律不同。当比值为1时，水平相关长度越大，平均安全系数越高，变异系数、失效概率越低，最危险滑面分布越集中，边坡越稳定；当比值为10时，水平相关长度越大，低黏聚力区越连续，越易出现边坡失稳破坏现象。

4) 内摩擦角与黏聚力的相关性直接影响边坡的稳定性，相关系数越大，平均安全系数越低，变异系数、失效概率越高，最危险滑面分布越分散，边坡的稳定性越差。

参考文献：

[1] LI K S, LUMB P. Probabilistic design of slopes[J]. Canadian Geotechnical Journal, 1987, 24(4): 520−535.

[2] GRIFFITHS D V, FENTON G A. Probabilistic slope stability analysis by finite elements[J]. Journal of Geotechnical and Geoenvironmental Engineering, ASCE, 2004, 130(5): 507−518.

[3] GRIFFITHS D V, HUANG J S, FENTON G A. Influence of spatial variability on slope reliability using 2-D random fields[J]. Journal of Geotechnical and Geoenvironmental Engineering, ASCE, 2009, 135(10): 1367−1378.

[4] SHEN Hong, FU Helin. Spatial variability and slope reliability analysis[J]. Electronic Journal of Geotechnical Engineering, 2011, 16(L): 1261−1276.

[5] CHO S E. Probabilistic assessment of slope stability that considers the spatial variability of soil properties[J]. Journal of Geotechnical and Geoenvironmental Engineering, ASCE, 2010, 136(7): 975−984.

[6] 谭晓慧, 王建国, 刘新荣, 等. 边坡稳定的有限元可靠度计算及敏感性分析[J]. 岩石力学与工程学报, 2007, 26(1): 115−122. TAN Xiaohui, WANG Jianguo, LIU Xinrong, el al. Finite element reliability computation and sensitivity analysis of slope stability[J]. Chinese Journal of Rock Mechanics and Engineering, 2007, 26(1): 115−122.

[7] 吴振君, 葛修润, 王水林. 考虑地质成因的土坡可靠度分析[J]. 岩石力学与工程学报, 2011, 30(9): 1904−1911. WU Zhenjun, GE Xiurun, WANG Shuilin. Reliability analysis of soil slope stability considering geologic origin[J]. Chinese Journal of Rock Mechanics and Engineering, 2011, 30(9): 1904−1911.

[8] 李典庆, 蒋水华, 周创兵. 基于非侵入式随机有限元法的地下洞室可靠度分析[J]. 岩土工程学报, 2012, 34(1): 123−129. LI Dianqing, JIANG Shuihua, ZHOU Chuangbing. Reliability analysis of underground rock caverns using non-intrusive stochastic finite element method[J]. Chinese Journal of Geotechnical Engineering, 2012, 34(1): 123−129.

[9] 李典庆, 蒋水华, 周创兵, 等. 考虑参数空间变异性的边坡可靠度分析非侵入式随机有限元法[J]. 岩土工程学报, 2013, 35(8): 1413−1422. LI Dianqing, JIANG Shuihua, ZHOU Chuangbing, el al. Reliability analysis of slopes considering spatial variability of soil parameters using non-intrusive stochastic finite element method[J]. Chinese Journal of Geotechnical Engineering, 2013, 35(8): 1413−1422.

[10] 蒋水华, 冯晓波, 李典庆, 等. 边坡可靠度分析的非侵入式随机有限元法[J]. 岩土力学, 2013, 34(8): 2347−2354. JIANG Shuihua, FENG Xiaobo, LI Dianqing, et al. Reliability analysis of slope using non-instrusive stochastic finite element method[J]. Rock and Soil Mechanics, 2013, 34(8): 2347−2354.

[11] 祁小辉, 李典庆, 周创兵, 等. 考虑土体空间变异性的边坡最危险滑动面随机分析方法[J]. 岩土工程学报, 2013, 35(4): 745−753. QI Xiaohui, LI Dianqing, ZHOU Chuangbing, et al. Stochastic analysis method of critical slip surfaces in soil slopes considering spatial variability[J]. Chinese Journal of Geotechnical Engineering, 2013, 35(4): 745−753.

[12] 肖特, 李典庆, 周创兵, 等. 基于有限元强度折减法的多层边坡非侵入式可靠度分析[J]. 应用基础与工程科学学报, 2014, 22(4): 718−732. XIAO Te, LI Dianqing, ZHOU Chuangbing, et al. Non-intrusive reliability analysis of multi-layered slopes using strength reduction FEM[J]. Journal of Basic Science and Engineering, 2014, 22(4): 718−732.

[13] ZIENKIEWICZ O C, HUMPHESON C, LEWIS R W. Associated and non-associated visco-plasticity and plasticity in soil mechanics [J]. Geotechnique, 1975, 25(4): 671−689.

[14] GRIFFITH D V, LANE P A. Slope stability analysis by finite elements[J]. Geotechnique, 1999, 49(3): 387−403.

[15] DAWSON E M, ROTH W H, DRESCHER A. Slope stability analysis by strength reduction[J]. Geotechnique, 1999, 49(6): 835−840.

[16] 栾茂田, 武亚军, 年延凯. 强度折减有限元法中边坡失稳的塑形区判据及其应用[J]. 防灾减灾工程学报, 2003, 23(3): 1−7. LUAN Maotian, WU Yajun, NIAN Yankai. A criterion for evaluating slope stability based on development of plastic zone by shear strength reduction FEM[J]. Journal of Disaster Prevention and Mitigation Engineering, 2003, 23(3): 1−7.

[17] 刘金龙, 栾茂田, 赵少飞, 等. 关于强度折减有限元方法中边坡失稳判据的讨论[J]. 岩土力学, 2005, 26(8): 1345−1348. LIU Jinlong, LUAN Maotian, ZHAO Shaofei, el al. Discussion on criteria for evaluating stability of slope in elastoplastic FEM based on shear strength reduction technique[J]. Rock and Soil Mechanics, 2005, 26(8): 1345−1348.

[18] 吕庆, 孙红月, 尚岳全. 强度折减有限元法中边坡失稳判据的研究[J]. 浙江大学学报(工学版), 2008, 42(1): 83−87. LÜ Qing, SUN Hongyue, SHANG Yuequan. Slope failure criteria of shear strength reduction finite element method[J]. Journal of Zhejiang University (Engineering Science), 2008, 42(1): 83−87.

[19] 孙冠华, 郑宏, 李春光. 基于等效塑性应变的三维边坡滑面搜索[J]. 岩土力学, 2010, 31(2): 627−632. SUN Guanhua, ZHENG Hong, LI Chunguang. Searching critical surface of three-dimensional slopes based on equivalent plastic strain[J]. Rock and Soil Mechanics, 2010, 31(2): 627−632.

[20] EL-RAMLY H, MORGENSTERN N R, CRUDEN D M. Probabilistic stability analysis of a tailings dyke on presheared clay-shale[J]. Canadian Geotechnical Journal, 2003, 40(1): 192−208.

(编辑 陈爱华)

Stability analysis of slope considering spatial variation of shear strength parameters

YUAN Wei1, 2, CHANG Xiaolin1, DUAN Yin1, 3, CHENG Yonggang1, MA Gang1

(1. State Key Laboratory of Water Resources and Hydropower Engineering Science, Wuhan University, Wuhan 430072, China;2. Hubei Provincial Water Resources and Hydropower Planning Survey and Design Institute, Wuhan 430064, China;3. Changjiang Institute of Survey, Planning Design and Research, Wuhan 430010, China)

A stochastic finite element method was proposed to analyze slope stability based on ABAQUS. Firstly, the Karhunen-Loeve (K-L) expansion method was used to build the random field model of shear strength parameters. Thereafter, the strength reduction finite element method was adopted to simulate the process of slope failure. The criteria for evaluating stability of slope were connectivity of plastic zone and convergence of numerical computation. Finally, the distribution of critical slip surfaces was determined by python script. The proposed method was used to study the effect of spatial variation of internal friction angle and spatial cohesion on the slope stability. The results indicate that the proposed stochastic finite element method is easy to operate and implement. It can analyze the effect of spatial variation of soil parameter on the slope stability from two aspects: safety factor and the critical slip surface. The stability of a slope with different correlation length of friction is similar. The variation trend of slope stability is contrary with two different ratio of horizontal correlation length to vertical correlation length while considering spatial variation of cohesion. Besides, as the correlation coefficient of soil parameters increases, the failure probability is higher, and the distribution of critical slip surface is wider.

spatial variation; slope stability; strength reduction finite element method; stochastic finite element method

10.11817/j.issn.1672-7207.2016.11.037

TU43

A

1672−7207(2016)11−3899−10

2016−01−08；

2016−03−27

长江科学院开发研究基金资助项目(CKWV2015224/KY)；国家自然科学基金资助项目(51379161) (Project (CKWV2015224/KY) supported by the CRSRI Open Research Program; Project(51379161) supported by the National Natural Science Foundation of China)

袁葳，博士研究生，从事高坝结构设计理论与数值仿真方面研究；E-mail: yw_0201@126.com