考虑流固耦合的深海采矿长输流硬管力学行为
2016-10-13李艳贾广成刘少军
李艳,贾广成,刘少军
考虑流固耦合的深海采矿长输流硬管力学行为
李艳1, 2,贾广成1,刘少军1, 2
(1.中南大学机电工程学院,湖南长沙,410083;2.深海矿产资源开发利用技术国家重点实验室,湖南长沙,410012)
利用Workbench软件建立深海采矿长输流硬管的流固耦合有限元模型,研究管长、顶端张力等因素对其固有频率的作用效果;分别在内流和外流作用下对硬管进行流固耦合动力学仿真,研究内流流速、内流密度、外流流速等对其力学特性的作用。研究结果表明:扬矿硬管的固有频率随着硬管长度的增加而降低,随着硬管所受的顶端张力的增加而增加;在内流作用下,扬矿硬管的最大侧向位移和最大主应力随着内流速度增大而增大,随着内流密度的增大而增大;在外部海流作用下,扬矿硬管的最大侧向位移和最大主应力随着外部海流速度增大而增大;为确保扬矿子系统高效平稳地工作,建议内流流速在合适的区间(如2.5~3.5 m/s)内变动,且整体深海采矿系统应在外部海流速度小于0.8 m/s条件下作业。
深海采矿;扬矿硬管;流固耦合;力学行为
扬矿子系统是深海采矿系统中的重要组成部分,承担着将海底集矿机采集到的结核矿石输送到海面采矿船的任务,同时又是电缆、动力部件等的安装载 体[1]。扬矿硬管作为扬矿子系统的关键组成部分,长达数千米,其工作特性不仅受内部输送的流体矿浆的脉动、压力变化等因素的影响,而且受外部海流、海浪等复杂载荷的作用,在内部和外部流场同时与扬矿硬管耦合的情况下,扬矿硬管容易产生较大的应力、应变,造成管道失效,影响整个深海采矿系统的开采效率,甚至造成破坏系统安全造成事故和损失,因此,有必要对扬矿硬管的流固耦合力学特性进行研究。HUANG等[2]运用排除伽辽金网格的方法(eliminated element Galerkin)研究不同边界条件下输液管道固有频率的变化,得到质量、刚度、长度及内部流体流速对输液管道固有频率的作用效果,但未考虑外部流体的影响。ACHOUYAB等[3]将管道因流固耦合作用产生的振动简化为平面梁的纵向和横向振动,使用有限元法和Newmark算法计算管道的位移,但忽略了流固耦合效应。刘建浩等[4]利用Abaqus软件对扬矿硬管在作业与拖航状态下的水平偏距与弯矩进行研究,但未考虑扬矿管内流体对管道的影响。为此,本文作者以中国深海采矿1 km海试系统为工程背景,针对深海采矿中的长输流硬管建立流固耦合有限元模型,考察管长、顶端张力等因素对其固有频率的作用效果;分别在内流和外流作用下对硬管进行流固耦合动力学仿真,考察内流因素、外流因素对其力学特性的作用,以便为深海采矿扬矿硬管设计及优化提供参考。
1 计算模型
1.1 扬矿硬管受力分析
扬矿硬管在作业过程中,会受到多种复杂载荷的耦合作用(如图1所示),这些作用力包括:扬矿硬管自身重力Y,内部流体重力L,海水浮力F,采矿船的拖曳力t,海洋波浪力B,海洋海流力H和顶端张力top[5−6]等。扬矿硬管在深海采矿系统作业过程中受力示意图如图1所示。在进行扬矿硬管力学行为分析时,不考虑采矿船拖曳力对扬矿硬管的影响。假设采矿船静止不动,即t=0。硬管系统上端与采矿船的升沉补偿系统相连接,扬矿硬管可以通过升沉补偿系统尽可能地保持与海平面垂直,建模时可假设硬管垂直于海平面。
扬矿硬管自身重力为
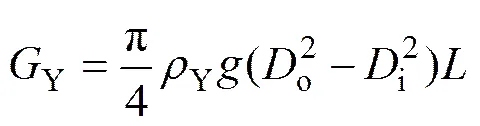
内部流体重力为
(2)
海水浮力为
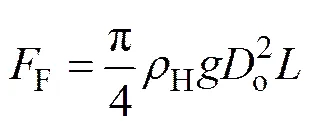
图1 深海采矿系统中扬矿硬管受力示意图
Fig. 1 Schematic force of lifting pipeline in deep-ocean mining system
扬矿硬管的直径相比于海流的波长很小,满足小直径刚体的条件,采用Morison方程[6]计算其所受海流力。波浪对扬矿硬管的作用力包括由波浪运动速度u产生的拖曳力F以及由波浪运动加速度产生的惯性力F。长度为d的扬矿硬管所受拖曳力为
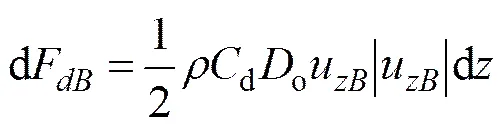
(5)
式中:为与长度为d扬矿硬管等体积的海水质量;;为距海面处的波浪运动的加速度;m为惯性附加阻力系数。则长度为d的扬矿硬管所受波浪作用力为
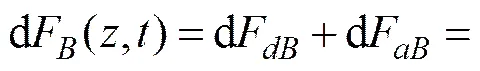
(6)
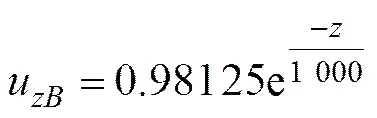
波浪运动加速度为
(8)
联合方程(6)~(8),可求得距海面处扬矿硬管单位长度所受的波浪作用力。
海流流经水下设备时,在其周围形成边界层。在边界层内部,海流会加速流动,加重摩擦力的作用效果,对物体作用很大的横向摩擦力。这个横向摩擦力在流动方向上的投影即为摩擦拖曳力f。海流流过物体后,在其后面产生很大的尾流,进而形成压力差,其方向是从前到后也就是沿着海流流动的方向。这种压力差作用在水下设备表面形成法向压力在流动方向上的投影即为压差拖曳力p[9]。
f和p与边界层内流体的流态、边界层分离点位置、水下设备外形及表面粗糙度等因素有关。长度为d的水下设备所受的海流力为

(9)
其中:d1和d2分别为摩擦拖曳力系数和压差拖曳力系数。令,则
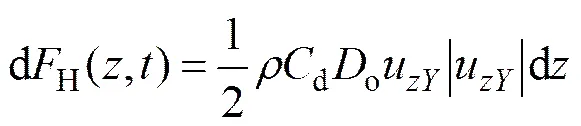
依照艾利波理论[10]以及中国深海采矿1 km海试系统工作区域海况,距海面深度为处的海流速度为
(11)
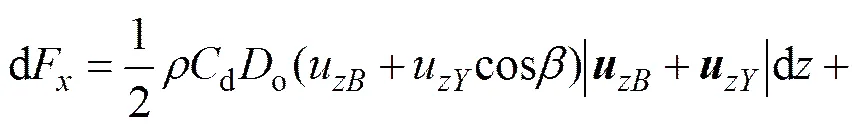
(12)
(13)
假设波浪与海流的运动方向一致,则距海面深度为处长度为d的柱体所受到的波流力为
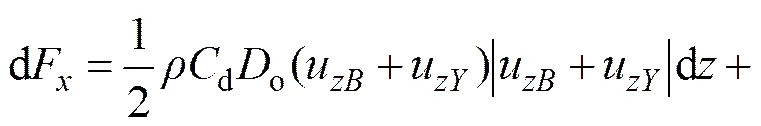
(14)
联合方程(7),(8),(11)和(14),便可以得出距海面处长度为d的扬矿硬管所受的波流作用力。
1.2 扬矿硬管的流固耦合数学模型
在整个深海采矿系统工作过程中,扬矿子系统内输运的流体为固液两相流。在分析内、外流与扬矿硬管的流固耦合作业时,为了更真实地反映实际工况,假定流体为不可压缩且具有黏性的宾汉流体[11−12]。流固耦合系统由流体区域和固体区域共同组成,采用位移−压力的关系描述内、外流体与扬矿硬管的流固耦合效应即固体采用位移作为传递变量,流体采用压力作为传递变量。在流固耦合分析中,为了传递位移变量,流体耦合面上的节点必须映射到固体耦合面的单元上;为了传递压力变量,固体耦合面上的节点必须映射到流体耦合面的单元上[13]。
扬矿硬管为线弹性材料,采用不可压缩宾汉型流体的Navier-Stokes方程作为流体运动的控制方程:
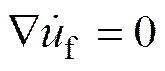
(16)
(17)
固体控制方程可以由牛顿第二定律导出:
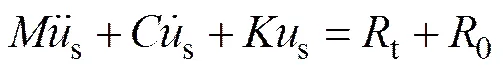
在流体与固体的耦合面上,流、固体单元具有相同位移和速度的边界条件:
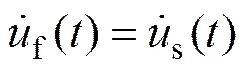
(20)
2 仿真与分析
2.1 扬矿硬管固有频率分析
2.1.1 扬矿硬管固有频率分析有限元模型
利用Workbench中的Geometry模块建立扬矿硬管和内部流体的有限元模型,然后通过Model模块对材料进行定义,对模型进行网格划分,并进行模态分析。扬矿硬管长度为900 m,硬管内径和外径分别为219.08 mm和193.68 mm,硬管的弹性模量为210 GPa,泊松比为0.3,密度为7 850 kg/m3,内流密度为1 123 kg/m3。扬矿硬管和内部流体分别采用三维八节点六面体的固体和流体单元。
扬矿硬管在深海采矿系统正常工作时,受到的浮力和自身重力均以分布载荷方式加载在扬矿硬管的单元上。扬矿硬管顶端与采矿船采用球型铰接连接,扬矿硬管底端与中间仓采用十字形铰接连接。在进行有限元分析过程中,假设扬矿硬管的顶端固定不动、底端自由,因此,在硬管顶端加载固定约束[14]。在进行仿真计算时,通过改变硬管的长度和顶端张力分析扬矿硬管固有频率变化规律。
2.1.2 扬矿硬管固有频率分析及结果
在对扬矿硬管进行模态分析过程中,分别设定硬管长度为600,700,800,900,1 000,1 100和1 200 m,对扬矿硬管的固有频率进行分析。图2所示为硬管前4阶固有频率随硬管管长增加的变化规律。从图2可知:扬矿硬管的一阶固有频率受扬矿硬管的管长变化的影响不大,而2,3和4阶固有频率随管长的增加而显著降低,且降低的幅度逐渐减小。应该综合考虑深海采矿作业深度、系统稳定性及安全性等因素,选取合适的扬矿硬管长度。
在对扬矿硬管进行模态分析过程中,分别设定扬矿硬管所受的顶端张力为−500,−200,−100,0,100,200和500 kN(负号表示受到的力是轴向压力)对扬矿硬管的固有频率进行分析。扬矿硬管所受的顶端张力对其固有频率的影响如图3所示。从图3可知:扬矿硬管的1和2阶固有频率受扬矿硬管所受的顶端张力变化的影响不大,而3和4阶固有频率随着顶端张力的增加而增加。通过调节扬矿硬管顶端张力的大小和方向可以在一定范围内改变扬矿子系统的固有频率,以免与海浪的频率接近发生共振。
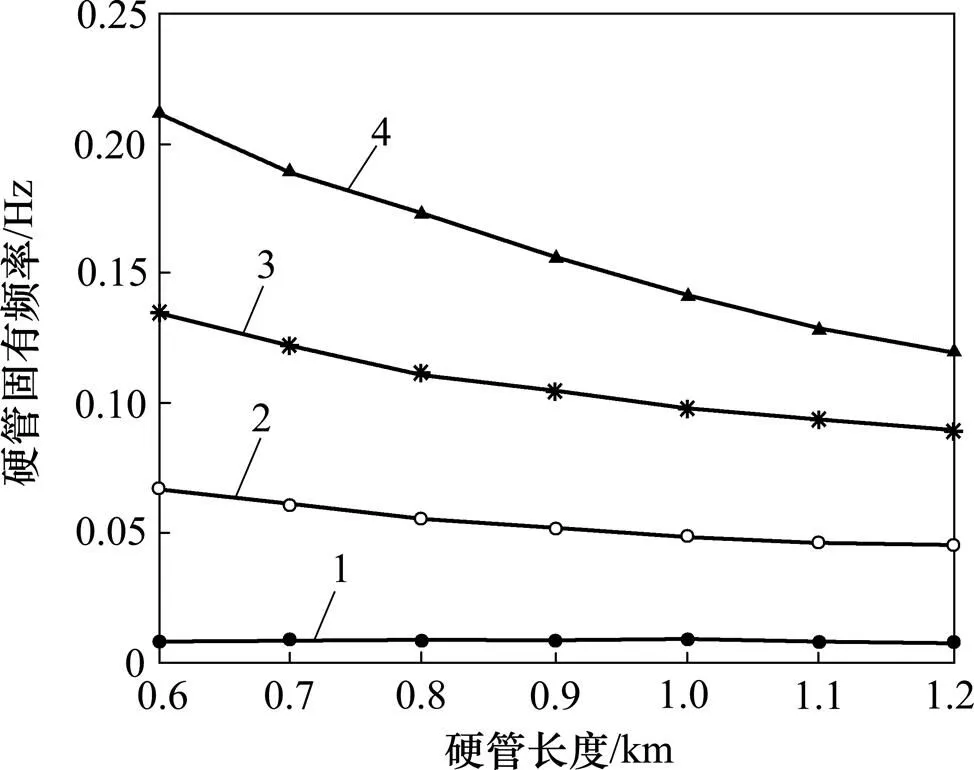
1—1阶频率;2—2阶频率;3—3阶频率;4—4阶频率。

1—1阶频率;2—2阶频率;3—3阶频率;4—4阶频率。
2.2 考虑内流的扬矿硬管流固耦合分析
2.2.1 扬矿硬管与内流的流固耦合有限元模型
扬矿硬管与内流的流固耦合作用属于双向流固耦合问题,内部流体的运动传递给硬管,而硬管的振动反向作用于内部流体。本文通过Workbench软件设置ANSYS和CFX的双向流固耦合进行分析。在Transient Structural模块中建立扬矿硬管和内部流体的三维实体模型,定义硬管的材料属性并进行网格划分。扬矿硬管受到的浮力和自身重力以硬管净重加载到硬管单元上,并在扬矿硬管的顶端施加固定约束。在CFX模块中定义内部流体属性参数进行网格划分,并设置流固耦合过程参数变量。选取硬管内壁和内流外表面为流固耦合交界面,建立如图4所示考虑内流的长输流硬管三维流固耦合模型。
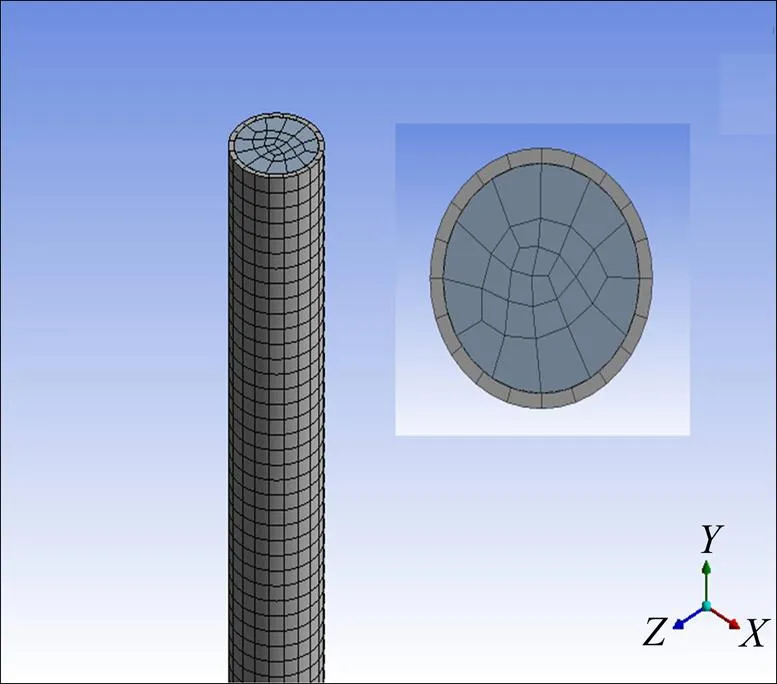
图4 考虑内流的长输流硬管三维流固耦合模型
在进行扬矿硬管与内流的流固耦合仿真过程中,先启动流体域计算并将得到的分析结果以力为变量传递给固体结构,再将固体分析得到的结果以位移为变量反向传递给流体,并且分析结果只在流固耦合交界面上进行传递[15]。在进行流固耦合仿真计算时,通过改变内流流速、内流密度分析内流作用下扬矿硬管的流固耦合力学行为。
2.2.2 内流作用下扬矿硬管流固耦合力学分析
在对扬矿硬管与内流进行流固耦合分析时,在Transient Structural模块中设定扬矿硬管长度为 900 m,内、外径分别为219.08 mm和193.68 mm,弹性模量为210 GPa,泊松比为0.3,密度为7.850 t/m3。在CFX模块中分别设定内部流体的流速为1.0,1.5,2.0,2.5,3.0,3.5,4.0,4.5和5.0 m/s,对内流作用下扬矿硬管流固耦合力学特性进行研究,结果如图5和图6所示。从图5和图6可知:硬管的最大侧向位移和最大主应力随着内流速度增大而增大,且当内流速度大于3.5 m/s时,硬管的最大侧向位移与最大主应力的增幅变大。这是因为内部流体在提升过程中流速非均匀分布于硬管横截面形成两侧流体速度差[16],内流速度越大,产生的速度差和侧向位移越大。内流的冲量作用于硬管产生的动载荷随着内流速度增大而增大,最大主应力也随着增大。过小的内流速度会导致系统效率降低甚至发生硬管堵塞等安全事故,而过大的内流速度会引起硬管的侧向位移过大而失稳。要使扬矿子系统高效平稳地工作,建议内部流体流速在合适的区间(如2.5~3.5 m/s)内变动。
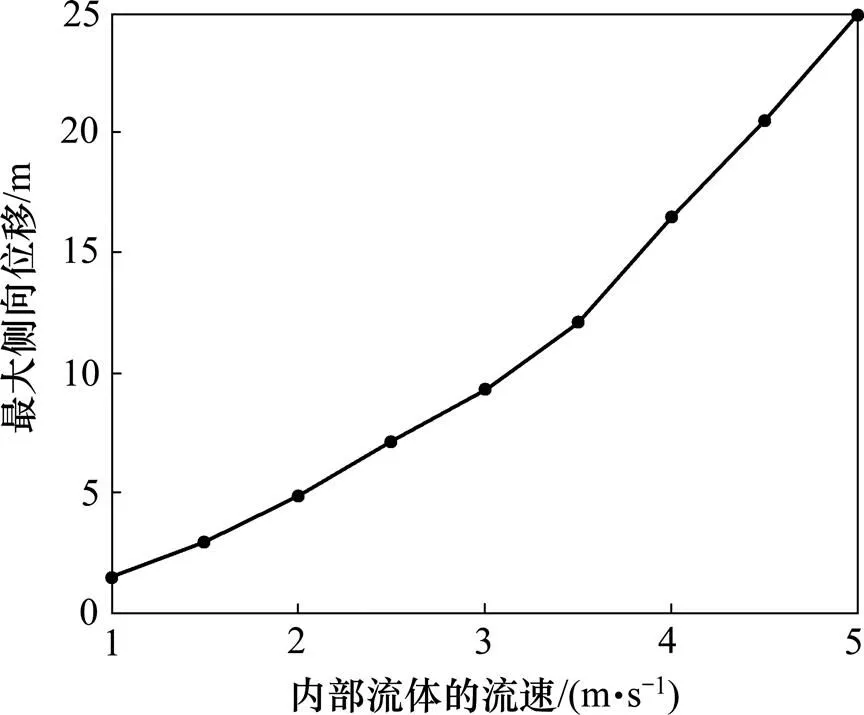
图5 硬管最大侧向位移与内部流体流速的关系
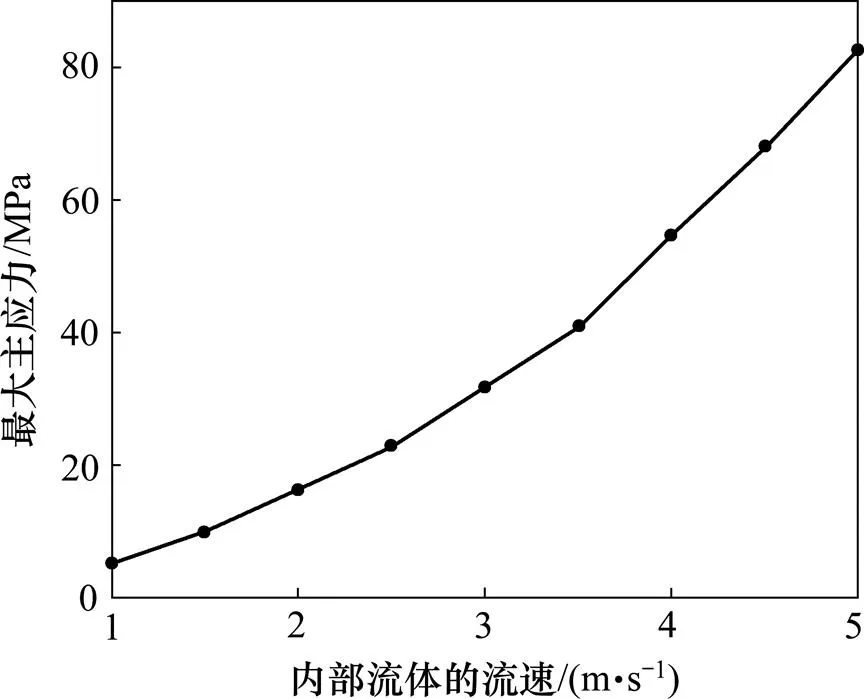
图6 硬管最大主应力与内部流体流速的关系
研究内部流体密度对内流作用下扬矿硬管流固耦合力学行为的作用效果,在Transient Structural模块中设定扬矿硬管长度为900 m,内径和外径分别为219.08 mm和193.68 mm,弹性模量为210 GPa,泊松比为0.3,密度为7.850 t/m3。在CFX模块中分别设定内部流体密度为0.800,1.000,1.123,1.200,1.500和2.000 t/m3,硬管最大侧向位移和最大主应力与内流密度的关系如图7和图8所示,可见:硬管最大侧向位移和最大主应力随着内流密度的增大而增大。通过增加集矿机破碎深海矿物结核和脱泥的时间,减小内部流体浓度和泥沙含量,使内流密度减小进而减小硬管的最大侧向位移和最大主应力,可提高扬矿子系统的稳定性。
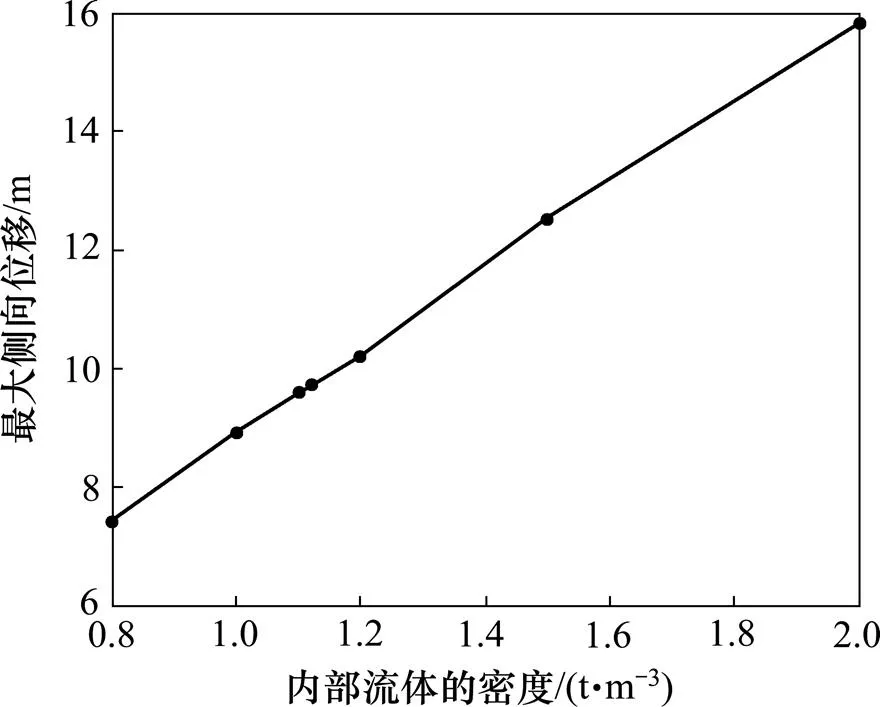
图7 硬管最大侧向位移与内部流体密度的关系

图8 硬管最大主应力与内部流体密度的关系
2.3 考虑外流的扬矿硬管流固耦合分析
2.3.1 扬矿硬管与外部海流的流固耦合有限元模型
由于扬矿硬管的变形对外部流场的影响基本可以忽略不计,只需考虑外部流场对扬矿硬管的作用,因此,外流作用下的流固耦合属于单向流固耦合问题。本文通过Workbench软件设置与FLUENT的单向流固耦合分析,在Static Structural模块中定义硬管材料属性并进行网格划分。受到的浮力和自身重力以硬管净重加载到硬管单元上,并在扬矿硬管的顶端加载固定约束。在FLUENT模块中建立扬矿硬管和外部海流的三维实体模型,定义外部海流属性参数,划分网格,并设置流固耦合过程参数。选取硬管外壁为流固耦合交界面,建立如图9所示考虑外流的长输流硬管三维流固耦合模型。

图9 考虑外流的长输流硬管三维流固耦合模型
在进行扬矿硬管与外部海流的流固耦合仿真过程中,在流固耦合交界面处的数据传递是单向的。外部海流的流体域计算得到的分析结果以力为变量传递给扬矿硬管进行固体结构分析,而固体分析结果不会再反向传递给流体。在进行流固耦合仿真计算时,通过改变外部海流流速分析外部海流作用下扬矿硬管的流固耦合力学特性。
2.3.2 外部海流作用下扬矿硬管流固耦合力学分析
在对扬矿硬管与外部海流进行流固耦合分析过程中,在Static Structural模块中设定扬矿硬管长度为900 m,内径和外径分别为219.08 mm和193.68 mm,弹性模量为210 GPa,泊松比为0.3,密度为7.850 t/m3。在FLUENT模块中分别设定外部海流的流速为0.15,0.30,0.45,0.60,0.75,0.87和1.00 m/s,对外部海流作用下扬矿硬管流固耦合力学特性进行研究(如图10和图11所示),可见:硬管的最大侧向位移和最大主应力随着外部海流速度增大而增大,且当外部海流速度大于0.80 m/s时,硬管的最大侧向位移和最大主应力的增幅变大。这是因为随着外部海流速度增大,扬矿硬管前后两侧流体域产生的压差增大,硬管的最大侧向位移和最大主应力也随着增大。过大的侧向位移易导致系统失稳,为了确保扬矿子系统高效稳定地工作,整个深海采矿系统应在外部海流速度小于0.80 m/s下作业。
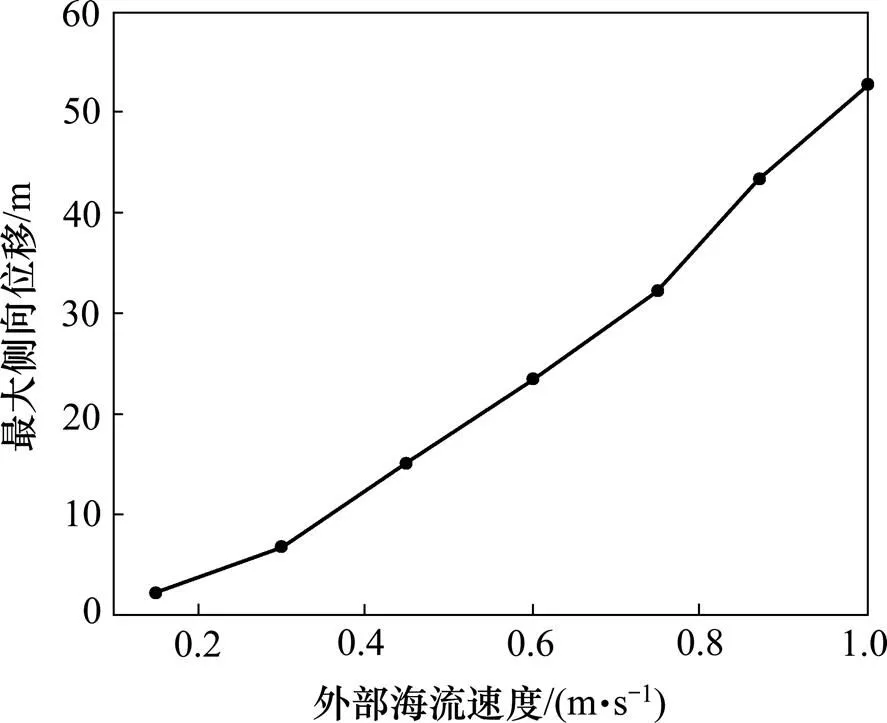
图10 硬管最大侧向位移与外部海流速度的关系
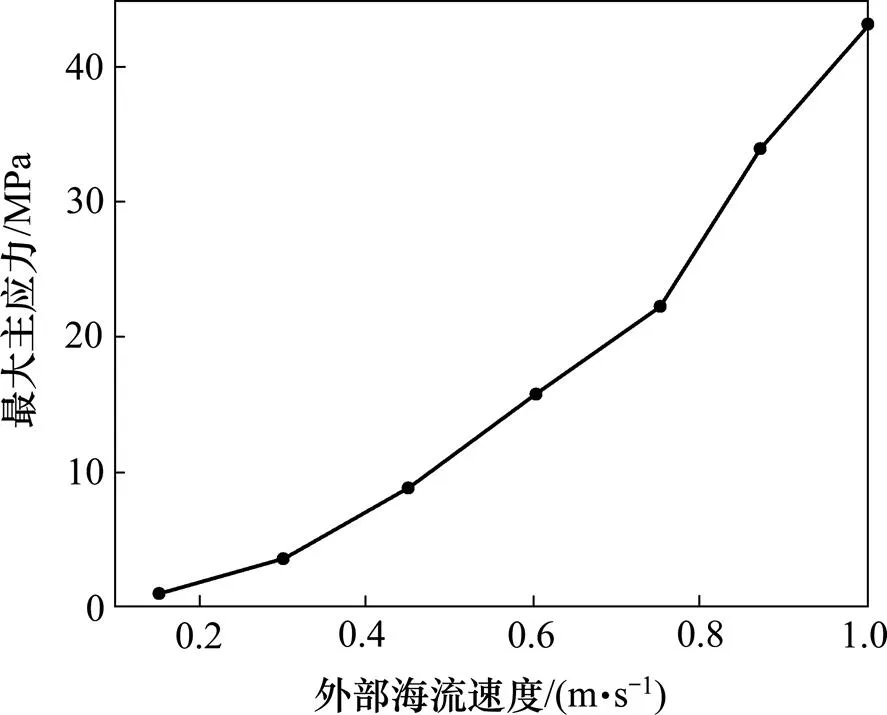
图11 硬管最大主应力与外部海流速度的关系
4 结论
1) 扬矿硬管的固有频率随着硬管管长的增加而降低,随着硬管所受的顶端张力的增加而增加。应综合考虑深海采矿作业深度、系统稳定性及安全性等因素,选取合适的扬矿硬管长度。可以通过改变扬矿硬管顶端张力的大小、方向,在一定范围内改变扬矿子系统的固有频率,避免硬管与海流的激振频率接近产生共振。
2) 硬管的最大侧向位移和最大主应力随着内流速度增大而增大,随着内流密度的增大而增大。要使扬矿子系统高效平稳地工作,建议内部流体流速在合适的区间(如2.5~3.5 m/s)内变动。通过采取一些措施减小内部流体质量−体积浓度和泥沙体积含量,使内流密度减小进而减小硬管的最大侧向位移和最大主应力,可改善扬矿子系统的稳定性。
3) 硬管的最大侧向位移和最大主应力随着外部海流速度增大而增大。过大的侧向位移易导致系统失稳,为保证扬矿硬管在作业过程中的稳定性,整个深海采矿系统应在外部海流速度小于0.80 m/s时作业。
参考文献:
[1] “十五”采矿海试系统总师组. 大洋多金属结核中试采矿系统l 000 m海上试验总体系统技术设计[R]. 北京: 中国大洋协会, 2004: 25−26. Chief Engineer Group of “Fifteen” Mining Sea Trial System. The overall system technology design of oceanic polymetallic nodule mining system l 000 m marine pilot test[R]. Beijing: China Ocean Mineral Resources R&D Association, 2004: 25−26.
[2] HUANG Yimin, LIU Yongshou. Natural frequency analysis of fluid conveying pipeline with different boundary conditions[J]. Nuclear Engineering and Design, 2010, 240(3): 461−467.
[3] ACHOUYAB E H, BAHRAR B. Numerical modeling of phenomena of water hammer using a model of fluid-structure interaction[J]. Comptes Rendus Mecanique, 2011, 339(4): 262−269.
[4] 刘建浩, 杨启. 深海采矿扬矿管的横向运动响应分析[J]. 矿山机械, 2012, 40(2): 5−9. LIU Jianhao, YANG Qi. Analysis on lateral motion response of deep-sea mining riser[J]. Mining Machinery, 2012, 40(2): 5−9.
[5] 刘金书, 禹宏云, 马慧坤. 6 000 m深海扬矿系统仿真分析[J]. 计算机仿真, 2009, 26(7): 333−336. LIU Jinshu, YU Hongyun, MA Huikun. Simulation analysis lifting system in a 6 km deep-ocean[J]. Computer Simulation, 2009, 26(7): 333−336.
[6] 周知进, 卢浩, 王钊, 等. 垂直提升管道输送过程中的流固耦合效应分析[J]. 中国海洋大学学报, 2013, 43(1): 87−92. ZHOU Zhijin, LU Hao, WANG Zhao, et al. Characteristics analysis on considering fluid-solid coupling effects for vertical lifting pipe[J]. Periodical of Ocean University of China, 2013, 43(1): 87−92.
[7] SANTILLAN S T, VIRGIN L N. Numerical and experimental analysis of the static behavior of highly deformed risers[J]. Ocean Engineering, 2011, 38(3): 1397−1402.
[8] NI Q, ZHANG Z L, WANG L. Application of the differential transformation method to vibration analysis of pipes conveying fluid[J]. Applied Mathematics and Computation, 2011, 217(16): 7028−7038.
[9] ZHOU Zhijin, YANG Ning, WANG Zhao. Analysis on shock wave speed of water hammer of lifting pipes for deep-sea mining[J]. China Ocean Eng, 2013, 27(2): 205−214.
[10] EROL H. Vibration analysis of stepped-pipe strings for mining from deep-sea floors[J]. Ocean Engineering, 2005, 32(1): 37−55.
[11] KERAMAT A, TIJSSELING A S, HOU Q. Fluid–structure interaction with pipe-wall viscoelasticity during water hammer[J]. Journal of Fluids and Structures, 2012, 28: 434−455.
[12] LIU Gongmin, LI Yanhua. Vibration analysis of liquid-filled pipelines with elastic constraints[J]. Journal of Sound and Vibration, 2011, 330(13): 3166−3181.
[13] 胡跃华, 蒋诚航, 闫怀磊, 等. 流固耦合作用下固支输液管道有限元分析[J]. 化工机械, 2012, 39(2): 190−193. HU Yuehua, JIANG Chenghang, YAN Huilei, et al. Vibration FEA of clamped fluid-conveying pipeline with fluid-structure interaction effect[J]. Chemical Machinery, 2012, 39(2): 190−193.
[14] AHMADI A, KERAMAT A. Investigation of fluid-structure interaction with various types of junction coupling[J]. Journal of Fluids and Structures, 2010, 26(7/8): 1123−1141.
[15] 梁建术, 王涛, 李欣业. 基于ANSYS Workbench的输液管道系统振动控制仿真研究[J]. 机械设计与制造, 2012(3): 187−189. LIANG Jianshu, WANG Tao, LI Xinye. Vibration control analysis of liquid-conveying pipe system based on ANSYS Workbench[J]. Mechanical Design and Manufacture, 2012(3): 187−189.
[16] LEE U, PARK J. Spectral element modeling and analysis of a pipeline conveying internal unsteady fluid[J]. Journal of Fluid and Structures, 2006, 22(2): 273−292.
(编辑 陈灿华)
Mechanical characteristics on long lifting pipeline in deep-ocean mining considering fluid-structure interaction
LI Yan1, 2, JIA Guangcheng1, LIU Shaojun1, 2
(1. School of Mechanical and Electrical Engineering, Central South University, Changsha 410083, China;2. State Key Laboratory of Exploitation and Utilization of Deep Sea Mineral Resources, Changsha 410012, China)
The influence of pipe length and top tension on the natural frequency of lifting pipeline was investigated based on the finite element model of fluid-structure interaction with Workbench software. In order to examine the influence of internal fluid velocity, internal fluid density and outflow velocity on the mechanical characteristics of lifting pipeline, dynamic simulations of fluid-structure interaction of lifting pipeline under the action of internal fluid and outflow were carried out. The results show that the natural frequency of lifting pipeline increases with the increase of top tension and the decrease of pipe length. With the impact of internal fluid, the maximum lateral displacement and the maximum principal stress of lifting pipeline increase with the increase of the velocity and density of the internal fluid. Under the influence of outflow, the maximum lateral displacement and the maximum principal stress of lifting pipeline increase with the increase of the velocity of the outflow. In order to ensure the safety and improve the efficiency of the lifting system, the velocity of the internal fluid must be controlled in suitable range (e.g. 2.5−3.5 m/s). The deep-ocean mining system should work with the velocity of outflow less than 0.8 m/s.
deep-ocean mining; lifting pipeline; fluid-structure interaction; mechanical characteristics
10.11817/j.issn.1672-7207.2016.11.008
TD807
A
1672−7207(2016)11−3670−07
2015−12−01;
2016−02−04
国家自然科学基金资助项目(51104177);国家高技术研究发展计划(863计划)项目(2012AA091201) (Project(51104177) supported by the National Natural Science Foundation of China; Project(2012AA091201) supported by the National High Technology Research and Development Program (863 Program) of China)
李艳,博士,副教授,从事机电液系统控制理论与技术、深海作业装备设计与控制研究;E-mail: lylsjhome@163.com
