考虑长径比和容许沉降影响的群桩SLS可靠度分析

边晓亚，郑俊杰，徐志军，章荣军



考虑长径比和容许沉降影响的群桩SLS可靠度分析

边晓亚1，郑俊杰1，徐志军2，章荣军1

(1. 华中科技大学岩土与地下工程研究所，湖北武汉，430074；2. 河南工业大学土木建筑学院，河南郑州，450052)

考虑桩正常使用极限状态(SLS)和承载能力极限状态(ULS)模型不确定性，利用概率统计理论，给出2种极限状态下单桩可靠度指标间的线性关系式。并结合群桩ULS可靠度分析方法，提出群桩SLS可靠度评估方法。最后，利用试桩资料，研究桩长径比(/)和容许沉降(lt)对群桩SLS可靠度分析结果的影响。研究表明：/对群桩SLS可靠度影响显著。无黏性土条件下，当/≤10或20＜/≤30时，都可取得较大的群桩SLS可靠度指标；黏性土条件下，当20＜/≤30时，可取得较大的群桩SLS可靠度指标。随lt的增加，估计的群桩SLS可靠度指标逐渐增大，但增大幅度逐渐减小，特别是当lt大于25 mm以后，随lt的增加，群桩SLS可靠度指标变化很小，此时承载力因素在桩基可靠度设计中起决定作用。

群桩；可靠度；正常使用极限状态；长径比；容许沉降

岩土工程中充满了不确定性[1]。在处理这些不确定性问题时，可靠度方法比安全系数法更具优势。当前，可靠度设计思想在许多国家、地区和组织制订的相关岩土工程设计规范中都有体现[2−3]。桩基础因其独特的优势在工程中得到广泛应用。工程上要求桩基要有足够大的承载力，尽量小的沉降。所以，进行桩基可靠性分析与设计，既要考虑承载力问题，又要关注沉降问题。通常情况下，确定基桩承载力的荷载试验没有进行到桩的失效状态，就可确定其满足工程需要，试验终止，这样就不能准确地得到桩承载力，从而不能准确地评价桩的可靠性。所以，基于沉降的正常使用极限状态就成为桩可靠性研究的重要方向。DITHINDE等[4]指出：在进行桩基础的极限状态设计时，应分别考虑承载能力极限状态和正常使用极限状态2个方面。无论是单桩还是群桩，关于承载能力极限状态可靠度的研究都已取得较多成果。ZHANG等[5]在群桩基础可靠度分析方面的工作是承载力可靠度分析方法由单桩系统发展到群桩系统的典型代表。一些学者已开始研究正常使用极限状态下的桩可靠度问题。PHOON等[6]针对输电线塔，讨论了基础正常使用极限状态下的可靠度设计问题。但该研究将容许沉降视为不变量，忽视了其变异性。WANG等[2,7]将容许沉降作为随机变量来解释计算模型不确定性，并提出了正常使用极限状态下建筑基础的可靠度计算方法。PHOON等[8]采用双曲线荷载–沉降模型，研究正常使用极限状态模型不确定性，为进行基桩可靠度分析提供了新思路。唐小松等[9]利用Copula理论，研究了钻孔灌注桩正常使用极限状态下的可靠性问题。迄今为止，关于群桩正常使用极限状态可靠性的研究成果不多。但是，群桩基础中桩–承台–地基土体系之间的相互影响，使得各单桩共同承担上部荷载，其沉降具有同步性。群桩这种承载特性和沉降机理使相关可靠性问题的研究得到了学者们的关注。本文作者通过正常使用极限状态与承载能力极限状态可靠度指标间的关系式，利用群桩承载力可靠度研究的已有成果，提出群桩正常使用极限状态可靠度分析方法。同时，研究了桩长径比(/)和容许沉降(lt)对群桩正常使用极限状态可靠度分析结果的影响。

1 基桩正常使用极限状态可靠度指标

承载力模型因子是衡量桩承载力模型不确定性的常用指标，取为承载力试计比(桩承载力的实测值与计算值之比)[4−5]，记为uls：

式中：uls和p分别为承载能力极限状态下基桩极限承载力实测值和计算值。众所周知，承载力计算模型的不确定性导致p的随机性，为研究方便，假设p服从对数正态分布。

基桩极限承载力uls是由所选择的失效准则决定的[10]。许多失效准则都采用荷载–沉降曲线来确定基桩承载力[11]。目前，国内外流行的基桩荷载−沉降关系模型很多，尤其以双曲线模型应用最为广泛[9]。文献[4,8]提出采用式(2)所示的标准化双曲线模型去描述实测荷载−沉降关系曲线。

式中：为桩顶沉降(mm)；为桩顶沉降达到时的作用荷载；和为荷载−沉降关系曲线的拟合参数。

据式(2)，若将桩沉降设计为某个容许极限值lt，则桩沉降达到此值所施加的荷载可作为正常使用极限状态下的极限承载力，记为sls，则有：

给出正常使用极限状态下的模型因子sls[4, 8]：

(4)

sls的变化规律可用来描述正常使用极限状态下模型的不确定性，其均值和变异系数计算公式如 下[4, 8]：

(6)

式中：μ和μ分别为和的均值；σ和σ分别为和的标准差；ρ,b为和的相关系数。

假设正常使用极限状态下基桩的可靠度指标为sls。参考文献[2,12]，推导可得sls的表达式如下：

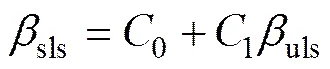
式中：uls为承载能力极限状态下基桩的可靠度指标；

(8)

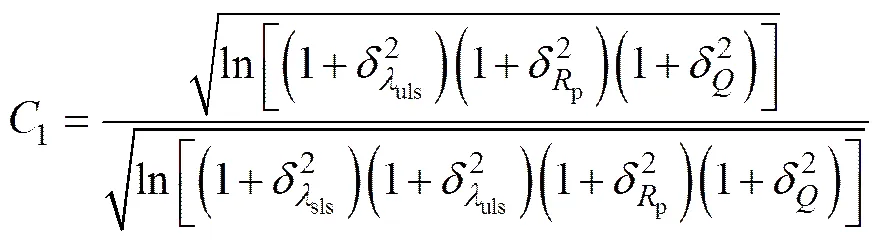
文献[2,12]表明，荷载变异系数δ对可靠度指标sls的影响很小。因此，在以下的研究中，δ都取0.5。

2 群桩承载力可靠度计算

基于基础荷载抗力系数设计法的基本原理，假设抗力和荷载效应都为服从对数正态分布的变量，且荷载效应组合仅考虑永久荷载和一种可变荷载，则利用一次二阶矩法可求出可靠度指标uls[13]：

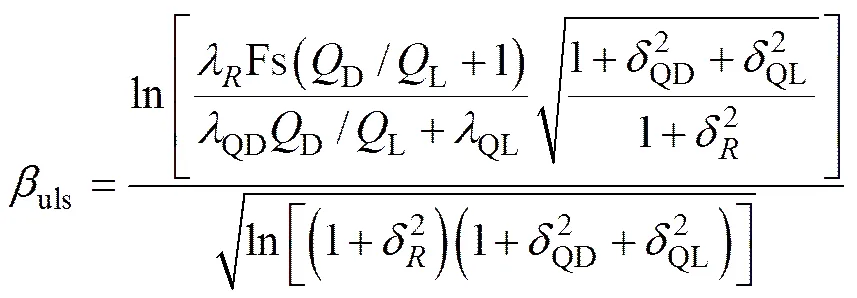
式中：D和L分别为永久荷载和可变荷载；λ，QD和QL分别为基桩极限承载力、永久荷载和可变荷载的偏差系数；δ，QD和QL分别为基桩极限承载力、永久荷载和可变荷载的变异系数；S为容许应力设计法中的安全系数，本文取为3.0；λ和δ常取基桩承载力试计比的均值和变异系数。

为方便计算，本文采用的荷载参数相关统计值如下[5]：QD=1.08，QL=1.15，QD=0.13，QL=0.18，D/L=3.69。

群桩基础中，利用群桩效应系数来衡量桩–承台–地基土相互作用效果，并将群桩效应系数定义为群桩整体极限承载力与群桩中各单桩极限承载力总和的比值[5]。

群桩效应系数与桩间距、桩数、桩径、桩的入土深度、桩的排列方式、承台宽度及桩间土的性质等因素有关，其中以桩间距为主要因素，另外，还应着重考虑承台效应对群桩承载力的影响。

ZHANG等[5]提出群桩效应系数服从对数正态分布，并给出了群桩效应系数的均值μ、标准差σ和变异系数等统计参数，见表1 (为尽量减少样本间的差异性，在本研究中，选取的群桩样本的桩间距都为3倍桩径)。

表1 群桩效应统计

系统效应源于群桩基础与上部结构之间的相互作用，通常通过系统效应系数来定量地评价群桩基础–上部结构体系协同作用的效果。系统效应系数定义为系统整体极限承载力与各群桩极限承载力总和的比值[5]。

BEA等[14]提出：导管架平台的系统效应系数为2.0，并建议系统效应的变异系数在0.1~0.2之间。AGGARWAL等[15]则认为：导管架平台的系统效应系数为1.2~1.3时，其变异系数介于0.17到0.18之间。文献[5]取系统效应的变异系数为=0.17，并且认为系统效应系数服从对数正态分布。

ZHANG等[5]给出了考虑群桩效应和系统效应时群桩基础整体承载力偏差系数和变异系数的表达式：

(12)

用式(11)和式(12)所示的群桩基础整体承载力偏差系数和变异系数来替代式(10)中的λ和δ，便可得到考虑群桩效应和系统效应时的群桩可靠度指标计算公式，群桩可靠度指标记为uls-G。

再将计算的群桩可靠度指标uls-G替代式(7)中的uls，便可得到群桩正常使用极限状态可靠度指标，记为sls-G。

3 讨论与分析

3.1 数据资料统计与分析

文献[4]收集了大量的基桩荷载试验资料，并按照试验区的土体类别和桩型，将试桩分为4类：无黏性土中打入桩、无黏性土中灌注桩、黏性土中打入桩和黏性土中灌注桩。

为研究桩长径比(/)和容许沉降(lt)对群桩正常使用极限状态可靠度分析结果的影响，本文仅依据试验桩所处场地土体性质的差异将试桩数据分为2类：无黏性土中试验桩(62根)和黏性土中试验桩(112根)。同时，依据/对每类试桩数据进行再次分类，各得到4个小类：/≤10，10＜/≤20，20＜/≤30和/＞30。

按照上述分类原则对试桩数据进行归类后，再对每一小类进行相关参数统计计算。其中与的均值和标准差及相关系数(ρ,b)的统计结果见表2。

若容许沉降lt取25 mm[2, 4]，则由表2中与的统计计算结果及式(5)和式(6)可得到模型因子和的统计特征及p的结果，见表3。

表2 a与b的均值和标准差及相关系数ρa,b

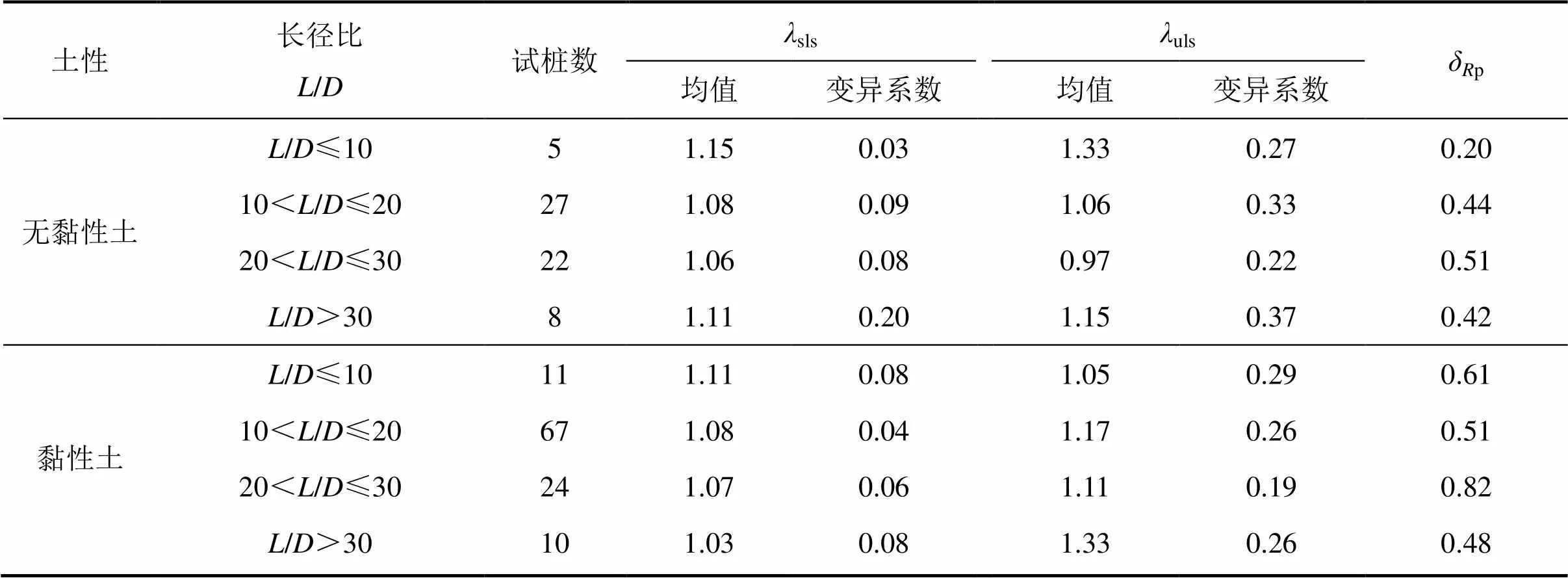
表3 模型因子λsls和λuls的统计特征及δRp

3.2 考虑长径比/对可靠度分析结果的影响

考虑到群桩可靠度分析中群桩效应和系统效应的作用，在研究/对群桩正常使用极限状态可靠度分析结果的影响时，分4类情况讨论：不考虑群桩效应和系统效应(此时：=1.00，=0；=1.00，=0)，考虑群桩效应而不考虑系统效应(此时：=1.00，=0)，考虑群桩效应和较弱的系统效应(此时：=1.50，=0.17)，考虑群桩效应和较强的系统效应(此时：=2.00，=0.17)。

由表3中相关参数的统计计算结果，并用本研究提出的群桩正常使用极限状态可靠度计算方法，可求得考虑/影响的群桩正常使用极限状态可靠度计算结果，见图1。

由图1(a)和图1(b)可知：随桩长径比/的变化，群桩正常使用极限状态可靠度指标曲线变化复杂：先下降，再上升，最后再次下降。表明/对群桩正常使用极限状态可靠度影响显著，且当/≤10和20＜/≤30时，群桩系统可取得较大的正常使用极限状态可靠度指标。

由图1(a)和图1(b)还可以看出：不考虑群桩效应和系统效应(1)、考虑群桩效应而不考虑系统效应(2)、考虑群桩效应和较弱的系统效应(3)和考虑群桩效应和较强的系统效应(4)4类情况所对应的可靠度指标随/变化曲线依次升高。表明群桩效应和系统效应在提高群桩可靠性方面效果显著。

由图1(c)和图1(d)可知：随/的变化，群桩正常使用极限状态可靠度指标曲线先上升，再下降，当20＜/≤30时，可靠度指标曲线达到一个极值点。表明仅当20＜/≤30时，群桩可以取得较大的正常使用极限状态可靠度指标。该结果与由图1(a)和图1(b)得出2个可靠度指标极值点的结果是有差别的，其原因在于土体性质的不同。

由图1(c)和图1(d)还可以看出：不考虑群桩效应和系统效应(1)、考虑群桩效应而不考虑系统效应(2)、考虑群桩效应和较弱的系统效应(3)和考虑群桩效应和较强的系统效应(4)4类情况所对应的可靠度指标随/变化曲线排列次序的变化情况，与由图1(a)和图1(b)得出的结果也具有明显的差异，这是由群桩效应的强度不同造成的。譬如，无黏性土高承台、无黏性土低承台、黏性土高承台和黏性土低承台4种条件下的群桩效应系数分别为1.41，1.40，0.83和1.04。具有大于1的群桩效应系数的群桩，其群桩效应提高了群桩的可靠性；而具有小于1的群桩效应系数的群桩，其群桩效应降低了群桩的可靠性。

综合图1(a)~1(d)可知，无论什么样的土体性质和承台条件，当20＜/≤30时，群桩都可取得较大的正常使用极限状态可靠度指标。这为基于正常使用极限状态的群桩可靠度优化设计提供了有益参考。研究建议在进行群桩设计时，长径比取20~30时，可靠性较高。

(a) 无黏性土高承台；(b) 无黏性土低承台；(c) 黏性土高承台；(d) 黏性土低承台

3.3 考虑容许沉降lt对可靠度分析结果的影响

容许沉降lt是群桩正常使用极限状态可靠度分析中的重要不确定性之一。因此，为考虑土体性质、承台条件、群桩效应、系统效应等因素的影响，研究容许沉降条件在群桩可靠度分析中的作用，现在考虑lt变化时，群桩正常使用极限状态可靠度指标的变化情况。为研究方便，此处取系统效应系数为1.25，其变异系数为=0.17。图2给出了群桩正常使用极限状态可靠度指标sls-G以及式(7)中的线性关系系数0和1随lt的变化情况。

由图2可知：随lt的增大，求得的群桩可靠度指标sls-G逐渐增大，但增长幅度逐渐降低，特别是当lt大于25 mm以后，可靠度指标就没有太大的改变。由此可见，当lt取得较大值后，正常使用极限状态条件对桩基可靠度设计将不再具有决定性影响。这时桩基础可靠度设计将依赖于承载力条件，满足承载能力极限状态可靠度设计条件的方案必然满足正常使用极限状态可靠度条件。该研究结果与文献[2]的结论是一致的。

在无黏性土高承台、无黏性土低承台、黏性土高承台和黏性土低承台4种条件下，纵然群桩可靠度指标sls-G随lt增大的趋势是一样的，但在群桩效应的影响下，可靠度指标值有较大的差异。这是因土体性质和承台类型的差异造成群桩效应的不同而引起的。

与可靠度指标随lt的变化规律相比较，由图2还可知，对于不同土体性质和承台类型的4种条件，无论线性关系系数0还是1，随lt变化的情况都具有高度的一致性。0随lt的增大而增大，但增大幅度逐渐降低，且也在lt大于25 mm以后，不再有较大的改变；但1始终保持在1附近，表明lt对其影响较小。另外，基于式(7)，0和1随lt的变化规律也解释了群桩可靠度指标sls-G随lt逐渐增大但增大幅度逐渐减小的结论。

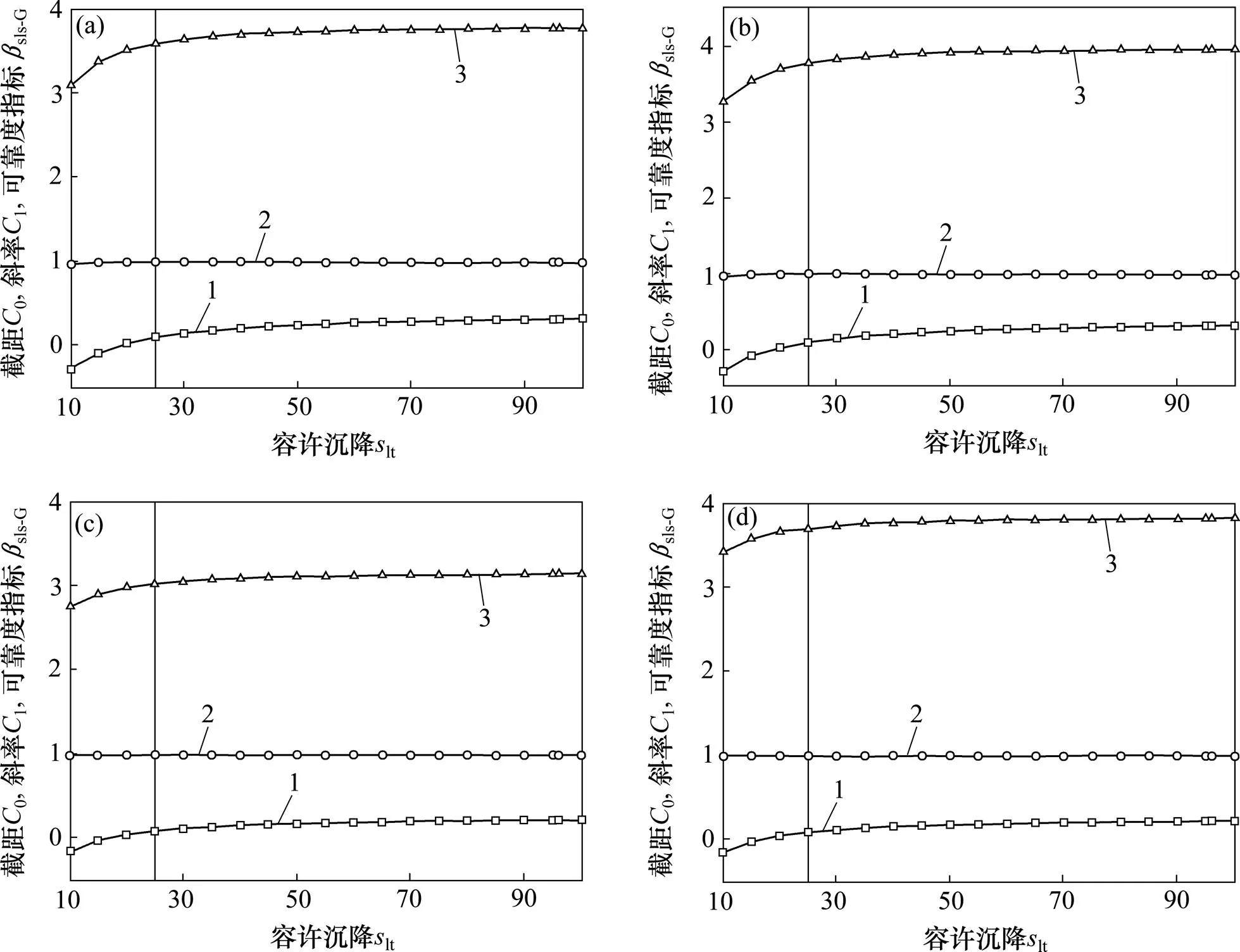
(a) 无黏性土高承台；(b) 无黏性土低承台；(c) 黏性土高承台；(d) 黏性土低承台

4 结论

1) 无黏性土条件下，当/≤10或20＜/≤30时，群桩可以取得较大的正常使用极限状态可靠度指标；黏性土条件下，当20＜/≤30时，群桩可以取得较大的正常使用极限状态可靠度指标。这为群桩基于正常使用极限状态的可靠度优化设计提供了有益参考，并建议在进行群桩设计时，长径比取在20到30之间，可靠性较高。

2) 对于不同土体性质和承台类型的4种条件，无论线性关系系数0还是1，随lt变化的趋势都具有高度的一致性。0随lt的增大而增大，但增大幅度逐渐减弱，且在lt大于25 mm以后，不再有较大的改变；但1却不因lt的变化而有较大改变，始终保持在1附近。

3) 随lt的增大，群桩可靠度指标sls-G逐渐增大，但增长幅度逐渐减弱，特别是当lt大于25 mm以后，可靠度指标几乎没有太大改变。因此，当在桩基可靠度设计中确定了较大的容许沉降lt时，承载能力极限状态条件将取代正常使用极限状态条件，在桩基可靠度设计中起主导作用。

参考文献：

[1] BAECHER G B, CHRISTIAN J T. Reliability and statistics in geotechnical engineering[M]. Chichester: John Wiley & Sons Ltd., 2003: 3−17.

[2] WANG Y, KULHAWY F H. Reliability index for serviceability limit state of building foundations[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2008, 134(11): 1587−1594.

[3] JGJ 94－2008, 建筑桩基技术规范[S]. JGJ 94－2008, Technical code for building pile foundations[S].

[4] DITHINDE M, PHOON K K, WET M D, et al. Characterization of model uncertainty in the static pile design formula[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2011, 137(1): 70−85.

[5] ZHANG L M, TANG W H, NG C W W. Reliability of axially loaded driven pile groups[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2001, 127(12): 1051–1060.

[6] PHOON K K, KULHAWY F H, GRIGORIU M D. Multiple resistance factor design for shallow transmission line structure foundations[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2003, 129(9): 807–818.

[7] WANG Y. Reliability index for serviceability limit state of drilled shafts under undrained compression[J]. Journal of GeoEngineering, 2009, 4(3): 113－118.

[8] PHOON K K. Reliability-based design in geotechnical engineering: computation and applications[M]. London and New York: Taylor & Francis, 2008: 344–384.

[9] 唐小松, 李典庆, 周创兵, 等. 基于Copula函数的基桩荷载-位移双曲线概率分析[J]. 岩土力学, 2012, 33(1): 171–178. TANG Xiaosong, LI Dianqing, ZHOU Chuangbing, et al. Probabilistic analysis of load-displacement hyperbolic curves of single pile using Copula[J]. Rock and Soil Mechanics, 2012, 33(1): 171–178.

[10] ZHANG L M, LI D Q, TANG W H. Reliability of bored pile foundations considering bias in failure criteria[J]. Canadian Geotechnical Journal, 2005, 42(4): 1086–1093.

[11] FELLENIUS B H. The analysis of results from routine pile load tests[J]. Ground Engineering, 1980, 13(6): 19–31.

[12] 边晓亚, 郑俊杰, 徐志军. 考虑参数和模型不确定性的基桩正常使用极限状态可靠度分析[J]. 岩土力学, 2014, 35(11): 3317−3322. BIAN Xiaoya, ZHENG Junjie, XU Zhijun. Reliability analysis for serviceability limit state of foundation piles considering parameter and model uncertainties[J]. Rock and Soil Mechanics, 2014, 35(11): 3317−3322.

[13] WHITMAN R V. Evaluating calculated risk in geotechnical engineering[J]. Journal of Geotechnical Engineering, 1984, 110(2): 143–188.

[14] BEA R G, JIN Z, VALLE C, et al. Evaluation of reliability of platform pile foundations[J]. Journal of Geotechnical and Geoenvironmental Engineering, 1999, 125(8): 696−704.

[15] AGGARWAL R K, LITTON R W, CORNELL C A, et al. Development of pile foundation bias factors using observed behavior of platforms during Hurricane Andrew[C]// Proc 28th Annu Offshore Technol Conf. Houston, TX, 1996: 445−455.

(编辑 杨幼平)

Reliability analysis for serviceability limit state of pile groups considering pile length-diameter ratio and limiting tolerable settlement

BIAN Xiaoya1, ZHENG Junjie1, XU Zhijun2, ZHANG Rongjun1

(1. Institute of Geotechnical and Underground Engineering, Huazhong University of Science and Technology, Wuhan 430074, China;2. School of Civil Engineering and Architecture, Henan University of Technology, Zhengzhou 450052, China)

The model uncertainties for serviceability limit state (SLS) and ultimate limit state (ULS) of piles were considered in order to establish a linear equation between the reliability indices for SLS and ULS of single piles using the probability and statistics theory. Then a method was presented to evaluate the reliability for SLS of pile groups in combination with the method of reliability analysis for ULS of pile groups. Finally, the influence of pile length-diameter ratio (/) and limiting tolerable settlement (lt) on the reliability analysis for SLS of pile groups was studied utilizing pile test data. The case study indicates that there existed the significant impact of/on the reliability indices for SLS of pile groups. And for non-cohesive soils, when/was smaller than 10 or between 20 and 30, the larger reliability indices for SLS of pile groups could be achieved. For cohesive soils, when/was between 20 and 30, the larger reliability indices for SLS of pile groups could be obtained. In addition, the reliability indices for SLS of pile groups generally increased with an increase ofltalthough the increase rate gradually diminished. Especially forltexceeding 25 mm, the variation of the reliability indices for SLS of pile groups was very small. So for largerltvalues, the ULS designs rather than the SLS designs played a decisive role in the reliability-based design of pile foundations.

pile group; reliability; serviceability limit state; length-diameter ratio; limiting tolerable settlement

10.11817/j.issn.1672-7207.2016.11.030

TU473

A

1672−7207(2016)11−3839−07

2015−12−11；

2016−02−21

国家自然科学基金资助项目(51278216，51308241)；教育部高等学校博士学科点专项科研基金资助项目(20130142120029)；河南工业大学高层次人才基金资助项目(2013BS010) (Projects(51278216, 51308241) supported by the National Natural Science Foundation of China; Project(20130142120029) supported by the Research Fund for the Doctoral Program of Higher Education of China; Project(2013BS010) supported by Henan University of Technology Fund for High-level Talents)

郑俊杰，博士，教授，从事岩土工程与隧道工程方面研究；E-mail: zhengjj@hust.edu.cn