基于稀疏表示的图像恢复方法

尚 丽，刘 韬，陈 杰，胡志峰

（苏州市职业大学 电子信息工程学院，江苏 苏州　 215104）

基于稀疏表示的图像恢复方法

尚 丽，刘 韬，陈 杰，胡志峰

（苏州市职业大学 电子信息工程学院，江苏 苏州 215104）

基于过完备字典的稀疏表示算法能够刻画图像的内在结构和先验属性，实现图像的最优逼近，目前在图像恢复中被广泛应用.但是，为获得精度更高的图像恢复效果，稀疏表示中仍存在一些关键问题需要进一步解决，如字典模型的构建、特征系数的优化稀疏分解、算法的收敛速度、噪声模型的估计、低维数据的线性不可分性等问题.鉴于此，本研究主要讨论基于稀疏表示的图像恢复方法，相关研究结果具有重要的理论研究意义和实用性.

稀疏表示；字典学习；过完备字典；特征提取；图像恢复

研究背景来源于国家自然科学基金项目（61373098），主要讨论稀疏表示算法及其在低分辨率图像恢复中的应用.在图像处理领域，对图像的表示模型和表示方式一直是一个根本性的问题，通常在图像处理之前，需要对图像数据进行有效地表示.可以说，对图像处理效果的好坏，首先决定于图像表示的方式.生理实验结果表明，大脑主视皮层V1区细胞对外侧膝状体细胞发放输出信息的特征表达存在超定性质，它的编码表达空间的维数大于其输入空间的维数［1-3］.这说明使用过完备基稀疏表示（sparse representation，SR）是神经信息群体分布式表达的一种有效策略.特别是当Olshausen和Field［3］于1996年在《Nature》杂志上指出自然图像本身存在稀疏性，提出了图像数据的稀疏性本质后，稀疏表示理论在图像处理领域得到有效的发展和应用.近几年，在图像处理领域已出现了大量有关稀疏表示算法及其应用的研究成果，这一问题成为目前又一新的研究方向和热点［1-3］.

低分辨率图像的恢复一直是个挑战性的课题.图像分辨率越高，图像细节就越精细，图像质量就越高.但是，由于通常获取高分辨率图像的手段主要依赖于成像器件，而价格昂贵的高精度成像仪器很难普及应用.同时，由于成像传感器技术的限制，有时获取高分辨率图像难度较大、成本很高，获得所需的高分辨率图像在很多场合下不现实，因此，利用图像超分辨率重建技术获得高分辨率图像具有重要的现实意义［4-5］.由于稀疏表示能够有效地实现图像的最优逼近，因此，本文在图像稀疏表示理论的基础上，结合一些成熟的机器学习算法和图像超分辨率恢复方法，主要探讨一些基于稀疏表示的低分辨率图像恢复方法，为低分辨率图像的处理提供一种新的研究途径.

1　稀疏表示原理

对一维信号进行稀疏分解的过程即是从过完备字典中选择具有最佳线性组合的若干原子来表示信号，这种逼近过程可以描述为［6-10］

对于图像而言，图像稀疏表示就是寻找一组基函数D，利用相对少的元素｛dki｝来表达原始图像，使投影所得的系数对于整个自然图像尽可能地统计无关，同时达到较高的逼近率，获得很小逼近误差也即是使“非零”系数尽可能的少，仅用少量的系数就能表示图像的主要特性.

2　基于改进稀疏表示的毫米波图像的超分辨率恢复

目前常用的稀疏表示为基于K-均值的奇异值分解（K-mean singular value decomposition，K-SVD）模型.在此模型中，稀疏优化分解算法常采用OMP（orthogonal matching pursuit）算法，训练过程比较慢［11-13］.为了提高训练速度，在稀疏表示的稀疏编码阶段，本文在快速稀疏编码（fast sparse coding，FSC）算法的基础上提出一种改进的FSC（modified FSC，MFSC）算法，进一步借助K-SVD模型，实现了高分辨率（high resolution，HR）和低分辨率（lowresolution，LR）字典的学习.

2.1改进的FSC模型

FSC算法与原始稀疏编码（sparse coding，SC）一样，都是图像的一种稀疏表示，但是FSC比SC具有更快的收敛速度，并且可以同时学习过完备基和完备基字典，可以灵活地提取信号中的内在结构.为了更有效地提取图像的细节结构和减少特征训练时间，考虑特征系数最大化稀疏分布和特征基的正交性，本文提出了一种新的FSC算法，其目标函数为［14］

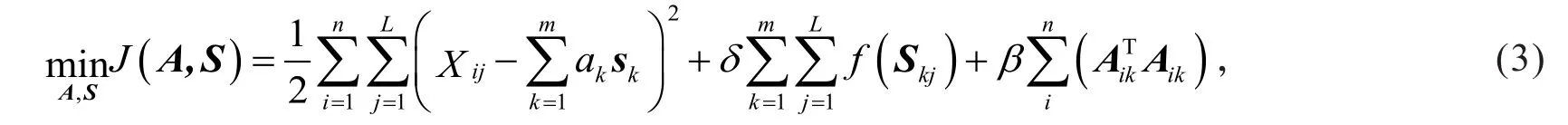
式中:（a）对应L1形式函数；（b）对应ε-L1形式函数；（c）对应对数函数.对A和S采用轮流迭代更新的方法对目标函数式（3）进行训练.注意到，更新A时，优化问题即是一个具有二次约束的最小二乘法问题.采用一般的凸优化求解法即可求解［15-20］.但是，一般的凸优化求解方法收敛的速度很慢，训练过程较长.为了加快最优特征基的收敛速度，当固定特征基时，仍采用FSC算法中的系数训练方法，借助特征符号搜索法实现稀疏系数的学习；对任意稀疏惩罚函数，采用拉格朗日对偶法（lagrange dual）求解L2约束最小二乘法问题以实现特征基的学习.在学习SC特征基时，这种优化算法比梯度下降方法更有效.

2.2特征基和稀疏系数的学习

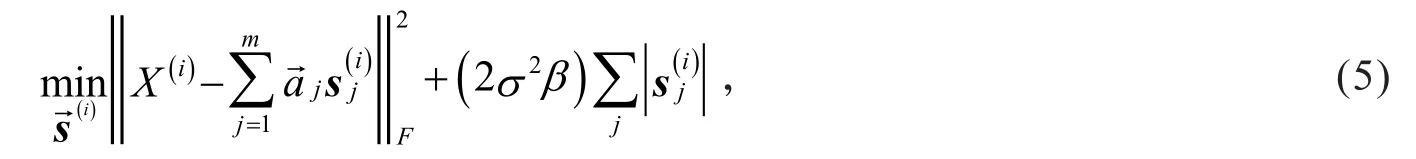
式中:y为表观测向量；z为输出向量；γ是一个常数.具体的特征符号搜索方法参见文献［14］，这里不再累述.

固定稀疏系数矩阵S，训练特征基A时的优化问题转化为如下目标函数

式中约束条件为.这是一个具有二次约束的最小二乘法优化问题，通常采用梯度下降优化算法求解即可，但是采用Lagrange对偶法求解的效果会更好.首先考虑拉格朗日形式

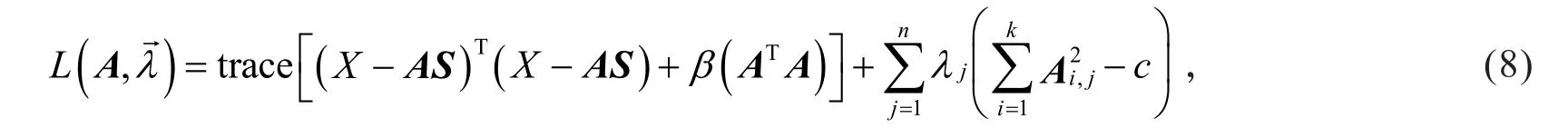
其中λj≥0为对偶变量.式（8）对应的拉格朗日对偶形式推导如下:

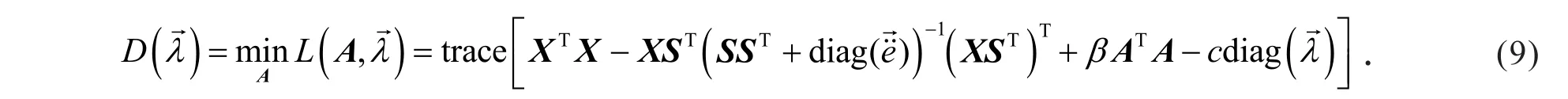
利用牛顿方法或者共轭梯度法可以优化式（9），则推导出特征基的更新形式

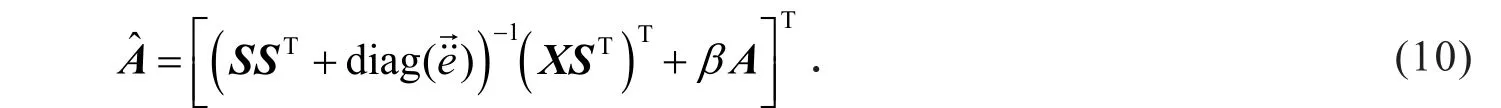
利用上述特征系数S和特征基A的学习步骤，轮流对S和A进行更新（更新一方时，另一方设为固定值），即可实现图像最佳特征的提取.

2.3实验结果与分析

测试中选用的几幅高分辨率HR图像图1（a）到图1（d）及其退化图像（即模拟的LR图像）如图1（e）到1（h）所示，毫米波（millimeter wave，MMW）图像（即真实的LR图像）及其原始图像成像目标如图1所示.对任意一幅图像进行图像分块处理，得到HR和LR子图像块训练集合.首先采用自然图像及其LR图像块集合对提出的算法进行仿真验证，训练得到的256个和1 024个原子的HR和LR字典分别如图2所示.显然，HR字典比LR字典具有明显的方向性和局部性.另外，考虑文章篇幅，这里仅给出256个原子时采用本文的稀疏表示算法对模拟的和真实的LR图像得到的恢复结果.作为实验对比，文中也给出了采用双三次插值（Bicubic）和邻域嵌入法（neighbour embedding，NE）得到的图像恢复的结果，如图3所示，显然，仅从视觉效果上看，采用本文的算法得到的恢复效果明显好于Bicubic和NE方法.

图1　原始图像及其退化图像

图2　自然图像的高低分辨率字典

为了进一步证明所提出的算法对图像恢复的效果，对恢复的自然图像的质量采用信噪比（signal noise ratio，SNR）作为评价指标；而毫米波图像的原始成像目标在实际应用是未知的，毫米波图像本身含有大量未知的噪声，因此对毫米波图像不适合采用SNR作为恢复图像的评价指标，这里采用相对信噪比（relative SNR，RSNR）作为毫米波MMW图像的评价指标.相应的计算公式为:

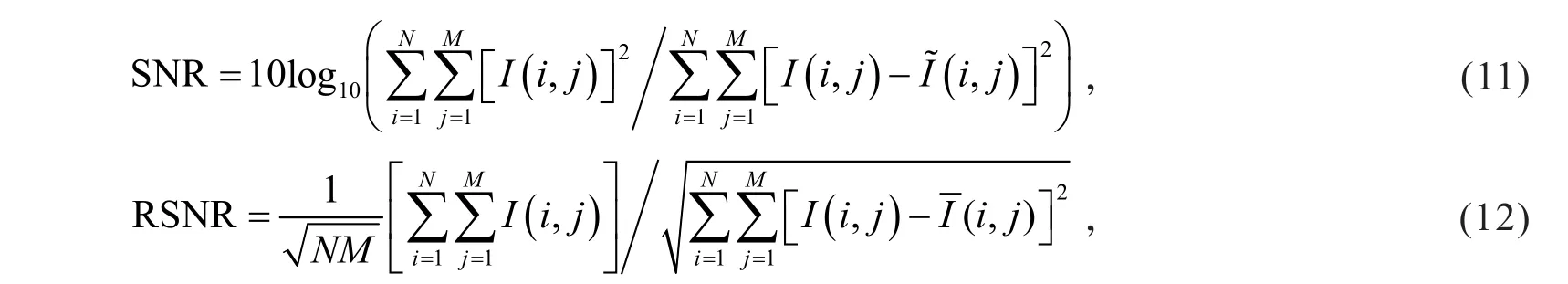
图3　不同算法下的图像恢复结果（稀疏表示方法中采用256个原子的字典）

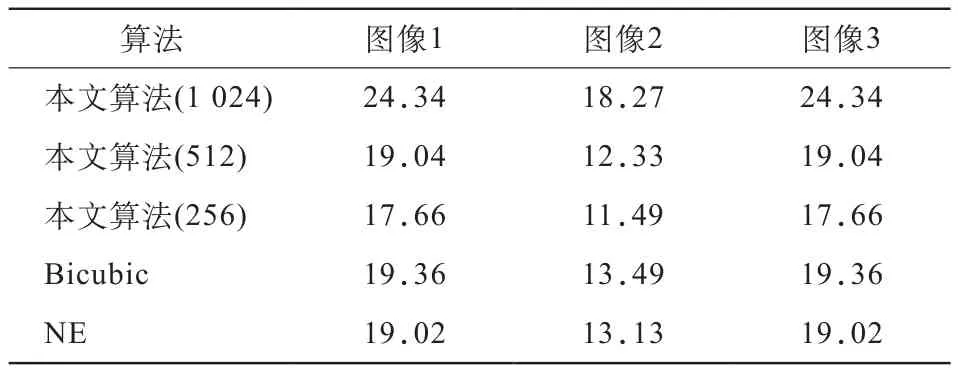
表1　采用不同算法得到的自然图像恢复结果的SNR值

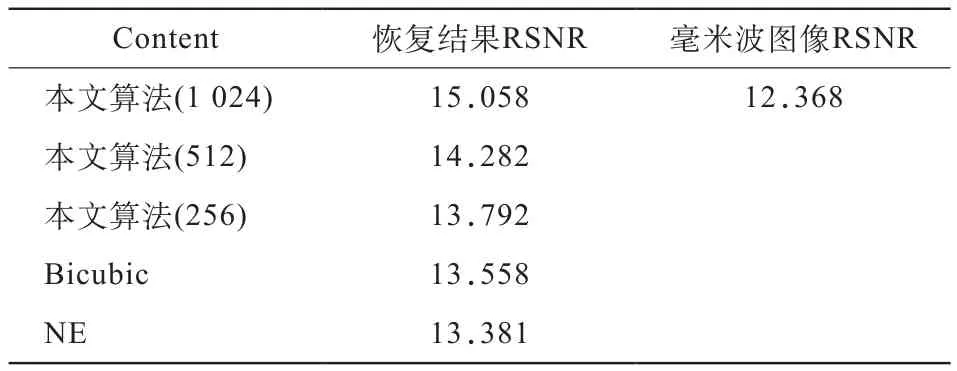
表2　采用不同算法得到的毫米波图像恢复结果的RSNR值

3　基于改进K-SVD消噪和RAMP的图像恢复

3.1改进K-SVD消噪模型

由于LR图像含有大量未知的噪声，对其进行预处理有助于提高后续的图像恢复质量.由于K-SVD稀疏表示已被证实在图像消噪中具有自适应和鲁棒性［21-25］，因此本文采用K-SVD（这里记作M-KSVD）消噪模型对LR图像进行预处理.假设无噪声图像I的噪声污染图像为为独立零均值高斯白噪声.如采用K-SVD方法直接对整幅图像进行操作，计算量太大，因此将LR图像随机划分为p×p大小的相互重叠的小块图像，使用稀疏字典D对每个子图像块进行像素的稀疏估计，而对于各重叠区域内存在多个估计值的像素点，对其求平均值，然后对各个子图像进行恢复，从而实现整幅图像的消噪，采用的消噪模型为［25］式中:为I的逼近值为字典D的估计为消噪图像中位置［i，j］的子图像在字典上的K-SVD稀疏表示的系数向量；RijI为从I中提取坐标为［i，j］.大小为p×p的子图像；Rij为一个二元矩阵；系数μij可以在学习中估计得到.

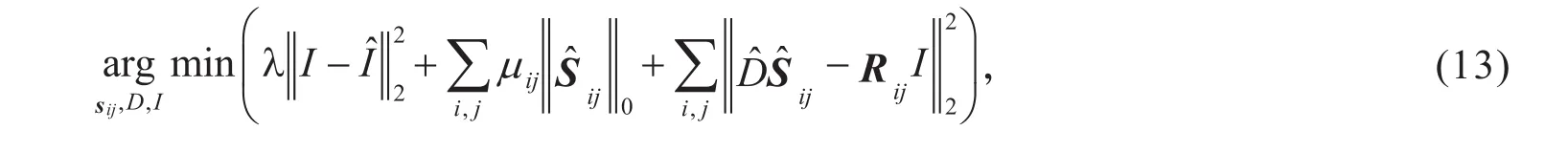
为了减少计算量，提高特征稀疏的稀疏度，在式（13）的基础上，提出一种改进的K-SVD模型

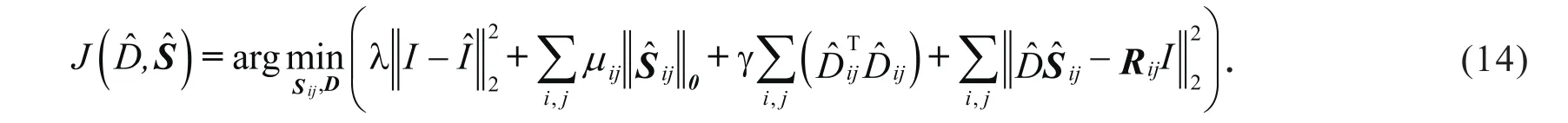
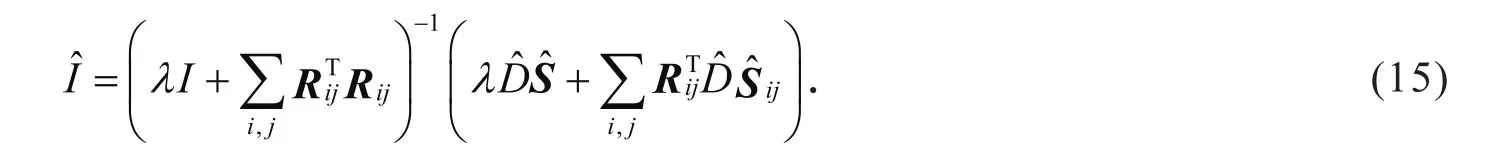
即可得到恢复的图像矩阵.

3.2RAMP算法

正则化自适应匹配追踪（regularized adaptive matching pursuit，RAMP）算法是一种新的贪婪算法［26］，其兼有正则化正交匹配追踪（regularized orthogonal matching pursuit，ROMP）和自适应匹配追踪（adaptive matching pursuit，SAMP）的优点，能够保证全局优化和收敛速度，可以在稀疏度未知时实现信号的精确重建.RAMP算法把同一个迭代过程分为多个阶段，用可变步长而不是稀疏度作为每次选择的原子数目，通过步长的不断增大逐步逼近稀疏度.该算法中关键的步骤是计算相关系数u，更新支撑集I和更新j步的残差rj.相关系数的计算公式为

式中Pj为观测矩阵P的第j列向量.

从系数中找出k个最大值对应的索引存入候选集J中.通过正则化将候选集J中的原子进行分组，选出能量最大的一组，其中原子的相关系数满足，则支撑集PZ更新公式为；对原始信号x的观测信号y，相应的残差更新公式为

3.3实验结果与分析

测试中采用Lena自然图像作为HR图像，其退化图像作为LR图像（见图1）.对LR图像首先进行K-SVD消噪处理，然后对HR图像和每一幅消噪后的图像进行分块处理，得到HR子图像块集合和LR子图像块集合.仍采用K-SVD稀疏表示思想训练HR和LR字典，在求解稀疏系数时采用RAMP迭代方法，对Lena图像的HR和LR子图像块集合分别进行训练得到的256维的HR字典DH和LR字典DL如图4（a）和图4（c）所示.为了说明基于RAMP的K-SVD算法在字典学习方面的有效性，在相同的实验条件下，文中也给出了采用基于OMP的K-SVD算法训练得到的256维字典，如图4（b）和图4（d）所示.比较图4中M-K-SVD和K-SVD算法得到的HR和LR字典，显然采用M-K-SVD算法得到的HR字典具有明显的方向性和局部性，而采用这两种算法得到的LR字典视觉特性较差.

不同噪声方差下，对Lena的LR图像利用M-K-SVD算法进行图像重构测试，得到的重构结果如图5所示.在噪声方差相同时，显然采用M-K-SVD算法得到的重构图像的视觉效果较好，特别是当噪声方差比较大时，该方法得到的重构图像的轮廓仍然容易辨认.为了进一步证明M-K-SVD算法的效果，这里采用SNR指标评价重构图像的质量，所得到的SNR值如表3所示，显然，噪声方差越小，不同算法得到的SNR值越大；在噪声方差相同时，M-K-SVD方法得到的SNR值明显大于K-SVD.实验结果证明了M-K-SVD算法在LR图像恢复中的性能.

图4　不同算法得到的HR和LR字典

图5　不同噪声方差和算法下得到的图像恢复结果

表3　不同噪声方差和算法下得到恢复图像的SNR值

4　基于模糊RBFNN和稀疏表示的LR图像恢复

4.1F-RBFNN的结构和算法

对径向基函数神经网络（radial basis function neural networks，RBFNN）隐层引入模糊逻辑，则构成一个四层的模糊RBFNN（Fuzzy RBFNN，F-RBFNN），其网络结构如图6所示［27-29］.

第一层为输入层，节点数n为一幅图像元素的个数；该层的各个节点直接与输入向量的各分量xi（i=1，2，…，n）连接，起着将输入数据传送到下一层的作用，该层的节点数为N1=n.

第二层为模糊条件层.节点输入为变量值xi，节点输出为隶属度值， 2，…，n；k=1，2，…，mi），n是输入量的维数，mi是xi的模糊分割数；该层的节点总数为.本文隶属度函数取高斯函数，其表达式为

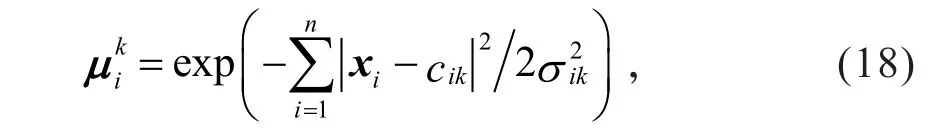
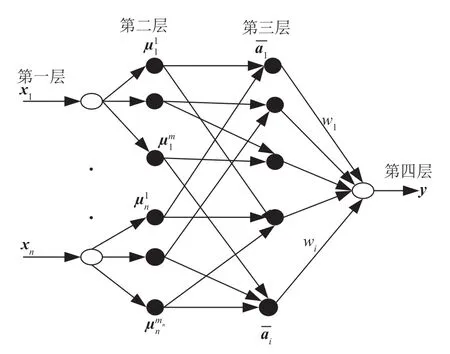
图6　F-RBFNN结构

式中:σik为第k个神经元中第i个高斯函数的宽度；cik为相应高斯函数的中心.

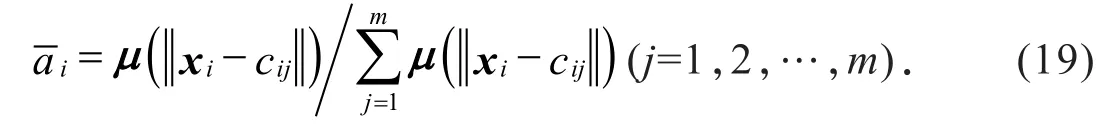
第四层为输出层，即反模糊层，网络总输出y为

式中:r为输出层的节点数；Wi为输出层权值向量.

为了实现快速学习，F-RBFNN网络参数的学习采用分离学习方法［27］，即cij和σij采用无导师监督的K-聚类方法学习；权值Wi采用有导师的在线学习方法训练，常用的方法是最速下降法，本文采用一种改进的最速下降法对Wi进行训练［28］，权值更新公式为

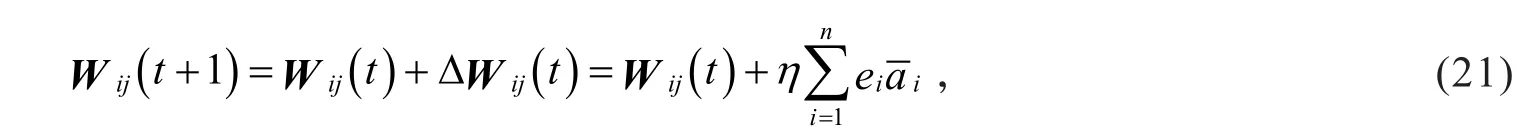
式中:ei为期望输出值与训练输出值之间的误差值，0≤η<1为学习速率.

4.2基于F-RBFNN和K-SVD图像消噪过程

首先利用F-RBFNN对LR图像中的未知噪声进行非线性滤波.训练时非线性函数f的建模模型为［30-32］

式中:γ>0为一常数；n（t）为白噪声；noise（t）为白噪声经过非线性函数后得到的结果.

然后，对F-RBFNN消噪后的图像再应用K-SVD方法实现图像局部自适应消噪，以得到分辨率更高的图像.K-SVD消噪的主要思想简述如下:假设无噪声图像Y的噪声污染图像为Y~=Y+n，假设为独立零均值高斯白噪声.将含噪图像Y~随机划分为p×p大小的相互重叠的小块图像，对这些子图像块进行K-SVD训练得到字典D，基于D对每个子图像块进行稀疏估计，在此过程中实现子图像块的消噪，最后对稀疏估计得到的子图像块进行平均，即可得到恢复的图像.

4.3实验结果与分析

实验中采用毫米波MMW图像作为LR测试图像，其成像模型和图像如图7所示.

首先利用F-RBFNN对图像进行非线性噪声逼近，采用式（22）的噪声模型.图像可以均匀交错分出两个子集，大小均为64×64像素，其中一个作为网络的训练样本X1，另一个作为检验样本X2.本文中的X1和X2分别由图像的奇数列和偶数列组成.然后，利用F-RBFNN逼近给定的噪声，从MMW图像中减去噪声即可得到非线性滤波结果.逼近的噪声图像和非线性滤波结果分别如图8（a）和图8（b）所示.进一步利用K-SVD法对F-RBFNN非线性滤波结果进行图像局部消噪.为了减少计算量，这一步不是针对整幅滤波图像处理，而是对其以每个像素点为中心抽取8×8的子图像块并进行列向量化和中心化，初始稀疏字典采用冗余离散余弦变换（DCT）构成，冗余度设为4.采用级联消噪方法得到的滤波结果如图8（c）所示，对应的稀疏字典如图8（d）所示.采用相对信噪比（relative SNR，RSNR）来评判其消噪图像的质量，相应的计算公式为

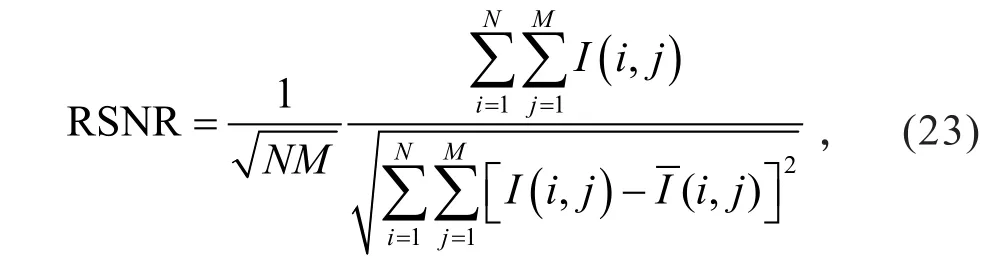
根据式（23），对F-RBFNN非线性滤波图像和本文级联消噪图像计算得到的RSNR值如表4所示.

图7　原始图像及毫米波系统成像图像

图8　F-RBFNN和K-SVD级联消噪结果

比较图7（b）和图8（c），很显然，图像中的噪声已大大减少，视觉效果较为理想，成像目标图像的轮廓很清晰地保留下来.再观察表4中的RSNR值，可以看出，无论是从视觉效果还是根据RSNR值的大小，F-RBFNN级联K-SVD的消噪方法都比本文用到的其他去噪方法有较好的图像恢复效果，实验结果证实了F-RBFNN+K-SVD方法的有效性.为了进一步说明F-RBFNN+K-SVD方法的有效性，文中也给出了F-RBFNN滤波、K-SVD自适应消噪以及小波软阈值消噪方法得到的实验结果.其中F-RBFNN+KSVD算法得到RSNR值最大，而小波软阈值消噪方法得到的恢复效果最差.因此，通过实验测试表明，对于含有大量噪声、分辨率较低的图像，F-RBFNN+K-SVD方法能够有效消除噪声、最大限度地保持图像的基本信息，恢复图像的目标轮廓边缘特征也较清晰，能够在一定程度上保证恢复图像的质量.

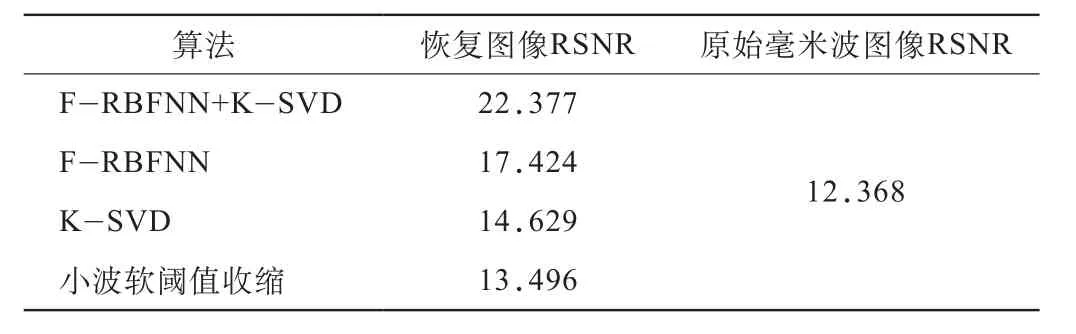
表4　不同算法得到的恢复图像的RSNR值

5　基于轮廓波变换和KSC收缩法的图像恢复

5.1轮廓波变换法

轮廓波变换能够较好地体现图像的几何结构，能够对图像进行多尺度、多方向性和局部性的表示.其变换过程归纳为［6-7］:①首先用拉普拉斯塔式滤波器（laplace pyramid，LP）对图像进行多尺度分解来捕捉奇异点.LP分解后得到一个逼近原始图像的低通子带和一个高通子带（由原始图像减去低通逼近图像得到），对于低通子带图像继续使用LP分解，就得到下一层的低通子带和高通子带，如此多次LP分解，就可以实现图像的多尺度分解；②对第①步得到的高通子带采用二维方向滤波器组（directional filter bank，DFB）将分布在同方向上的奇异点合成为轮廓段.DFB的作用是捕获高频信息，对带通子带图像进行dk级方向分解，产生2dk个楔形子带，每个子带分别代表一个方向.原始图像经LP-DFB结构多层分解后，即得到多尺度、多方向的子带图像，图9给出了轮廓波变换的原理图.

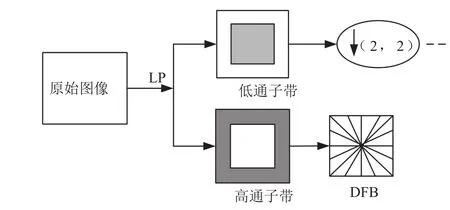
图9　轮廓波变换原理图

经过轮廓波分解，得到的小尺度子带内为高频信息，含噪声信息较多；大尺度子带噪声较少，噪声方差较小.不同尺度的噪声方差由下式估计为

式中:Bij为轮廓波对含噪图像进行第一层分解后的高频系数；l为轮廓波分解层数（或尺度）.

5.2KSC收缩法

考虑特征系数的稀疏性和独立性以及图像的结构和内容，提出了一种新的基于峭度评判标准的稀疏编码（kutosis based sparse coding，KSC）模型［5］，其目标函数定义为

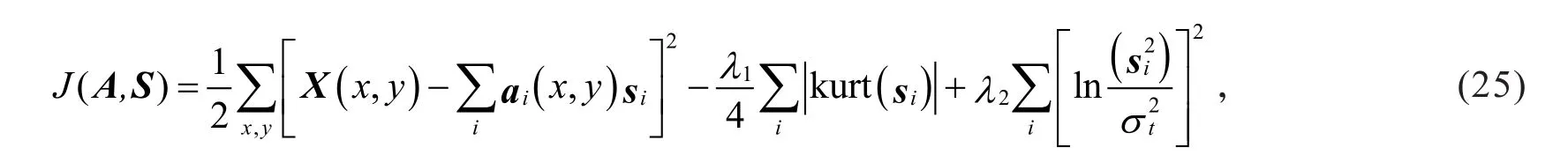
式中:X（x，y）为n维原始图像像素值；ai（x，y）为n×m维特征矩阵A的第n列向量；si为m维系数矩阵S的第i行向量为给定的系数方差尺度标量（E｛·｝表示求数学均值）；λ1和λ2均为正的常数为峭度的绝对值，采用最小化-，就是最大化si的稀疏性.假设向量si具有零均值，则的函数形式为

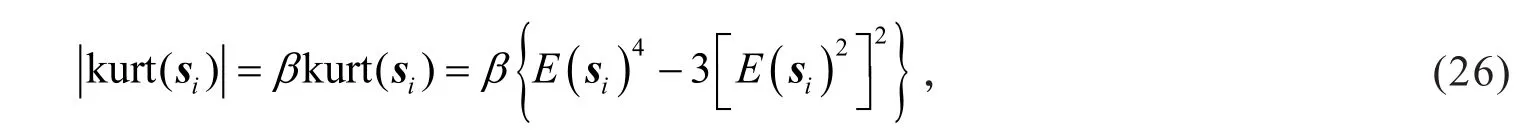
式中:当峭度为负时，β=-1；反之，β=1.

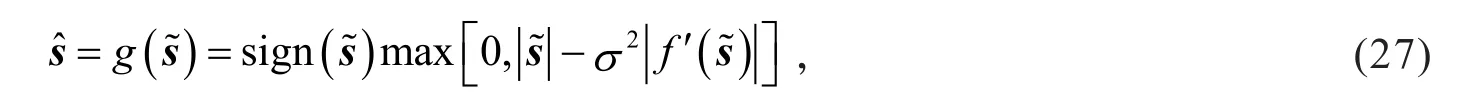
把式（28）代入式（27）即得到消噪所需收缩函数.

结合KSC算法和收缩函数，基于KSC收缩KSCS（KSC based Shrinkage）的过程简述如下:

1） 选用m幅图像，用KSC算法进行训练，得到特征基矩阵A并使A正交化，求出其逆阵W；

对各层高通子图像应用上述步骤进行自适应阈值消噪，并对消噪后的各层分解图像进行轮廓波逆变换后，即得到消噪后的各子带图像.

5.3实验结果和分析

选用图像作为真实的LR图像，选用Lena图像及其退化图像作为模拟的LR图像.对每一幅LR图像采用2层、每层4方向的轮廓波变换得到的结果如图10所示.可以看出分解得到的第一个低通子带图像包含了原目标图像的大部分能量，图像轮廓被保持下来，如图10（a）和10（d）所示；而噪声的大部分能量被集中到了第一层分解得到的高通子带图像，如图10（b）和10（e）所示.对高通子带图像应用式（24）可以估计出不同尺度的噪声方差，然后应用KSC收缩法可对高通子带图像进行消噪，对图像轮廓波变换的2层4方向高通子带图像进行KSCS消噪的结果如图11所示，对Lena退化图像轮廓波变换的2层4方向高通子带进行KSCS消噪的结果如图12所示.

图10　图像和Lena退化图像的轮廓波变换结果

表5　不同噪声方差和不同算法下得到的Lena恢复图像的SNR值

随机选取10幅大小相同的自然图像来学习KSC模型.用一个8×8像素的滑动子图像窗口随机采样每一幅图像5 000次，组成一个64×50 000的训练数据集.对进行中心化PCA降维预处理，得到具有零均值和单位方差的数据X，X即作为KSC模型的训练样本.采用KSC算法训练得到稀疏特征系数后，应用KSCS方法对各层高通子带图像进行自适应阈值去噪，然后对去噪后的各层高通子带图像再应用轮廓波逆变换即可恢复出原始图像.为了比较本文算法的消噪效果，分别采用KSCS和轮廓波变换等方法进行比较实验，并采用SNR指标评价Lena图像的恢复效果，采用RSNR指标评价图像的恢复效果.2幅Lena退化图像的恢复结果和图像恢复的结果如图12所示.可以看出，各算法对背景噪声都有较大程度地减弱，对目标的轮廓都能够较好地恢复.但是，仅用肉眼很难判断不同算法得到的恢复图像的优劣，必须借助评价指标来进行评判.不同噪声方差下恢复的Lena图像的SNR值如表5所示，而图像恢复的RSNR值如表6所示.上述实验结果从理论上证实本文提出的基于轮廓波的KSCS消噪方法对LR图像具有明显的降噪作用，同时也优于KSCS和轮廓波变换方法.由此证实，对于未知噪声方差的图像，结合轮廓波和KSCS的算法能够在很大程度上消除噪声，能够最大限度地保持LR图像的基本信息和视觉特性，目标轮廓边缘特征也较清晰，可以在一定程度上保证恢复图像的视觉质量.

图11　2层4方向的图像的高通子带进行KSC收缩的结果

图12　2层4方向的Lena退化图像的高通子带进行KSC收缩的结果

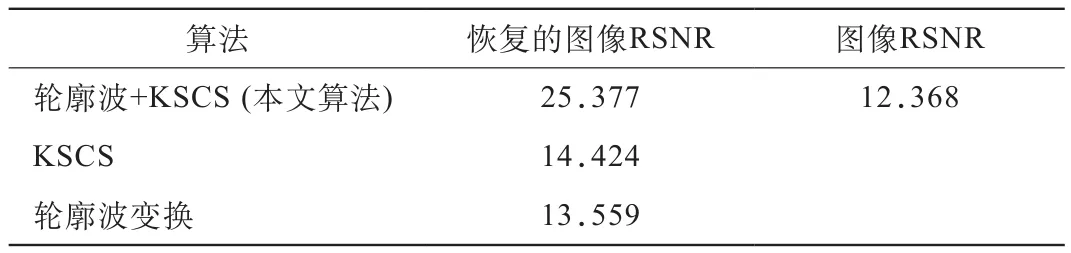
表6　不同算法下消噪图像相对图像得到的RSNR值

图13　不同算法得到的恢复图像

6　结论

主要讨论了稀疏表示模型的构建及其优化学习方法，同时结合已成熟的机器学习方法和图像恢复技术，进一步探讨了这些稀疏表示在低分辨率图像恢复中的应用.文中主要考虑了稀疏表示中仍然存在的一些关键问题，如字典模型的构建、稀疏特征系数的快速优化算法、字典学习的收敛速度、噪声模型的估计等问题.针对这些问题，在K-SVD稀疏表示框架的基础上，结合快速稀疏编码、轮廓波变换、稀疏编码收缩等技术，提出了一些新的低分辨率图像恢复方法.采用模拟的低分辨率图像和真实的低分辨率图像（毫米波图像）进行测试，所得到的测试结果验证了所提出方法的有效性.但是，由于稀疏表示适用于数据线性特征的学习，对非线性特征的提取几乎无能为力，同时稀疏表示用于分类问题中时，分类的精度也有待于提高，这些也是本文进一步研究的目标.

［1］ HOYER P O.Non-negative matrix factorization with sparseness constraints ［J］.Journal of Machine Learning Research，2004（5）:1427-1469.

［2］ ELAD M.Sparse and redundant representation:from theory to applications in signal and image processing ［M］.New York:Springer，2010:228-237.

［3］ OLSHAUSEN B A，FIELD D J.Emergence of simple-cell receptive field properties by learning a sparse code for natural images ［J］.Nature，1996，381:607-609.

［4］ 耿则勋，陈波，王振国，等. 自适应光学图像复原理论与方法［M］. 北京:科学出版社，2010.

［5］ YANG S，WANG M，CHEN Y，et a1.Single-image super-resolution reconstruction via learned geometric dictionaries and clustered sparse coding ［J］. Image Processing，IEEE Transactionson，2012，2l （9）:4016-4028.

［6］ 尚丽，苏品刚. 基于K-SVD的偏微分方程模型在毫米波图像恢复中的应用［J］. 计算机应用，2012，32（3）:756-758.

［7］ YANG J C，WRIGHT J，MA Y，et al.Image super-resolution as sparse representation of raw image patches ［C］// Proceedings of the 2008 IEEE Computer Society Conference on Computer Vision and Pattern Recognition.Anchorage:IEEE Press，2008:1-8.

［8］ YANG J，WANG Z，LIN Z，et al.Coupled dictionary training for image super-resolution ［J］.IEEE Transaction on Image Processing，2012，21 （8）: 3467-3478.

［9］ WANG S Q，ZHANG J H.Fast image inpainting using exponential threshold POCS plus conjugate gradient ［J］.The Imaging Science Journal，2014，62（3）:161-170.

［10］ YANG Jian chao，WRIGHT J，HUANG T，et al，Image super-resolution via sparse representation ［J］.IEEE Transactions on Image Processing，2010，19:2861-2873.

［11］ AHARON M，ELAD M，BRUCKSTEIN A，et al.K-SVD:an algorithm for designing overcomplete dictionaries for sparse representation ［J］. IEEE Transactions on Signal Processing，2006，54（11）:4311-4322.

［12］ SHANG Li，SU Pin gang，LIU Tao，et al.Denoising MMW image using the combination method of contourlet and KSC shrinkage ［J］. Neurocomputing，2012，83:229-233.

［13］ MAIRAL J，BACH F，PONCE J，et al.Online learning for matrix factorization and sparse coding ［J］.Journal of Machine Learning Research，2010（11）:19-60.

［14］ SHANG Li.Modified sparse representation based image super-resolution reconstruction ［J］.Lecture Notes in Computer Science （LNCS），2015，9225:491-497.

［15］ RAUHUT H，SCHNASS K，VANDERGHEYNS T，et al.Compressed sensing and redundant dictionaries ［J］.IEEE Transactions on Information Theory，2008，54:2210-2219.

［16］ MAIRAL J，BACH F，PONCE J，et al.Online learning for matrix factorization and sparse coding ［J］.Journal of Machine Learning Research，2010（11）:19-60.

［17］ ELDAR Y C，BOLCSKEI H.Block-sparsity:coherence and efficient recovery ［J］.IEEE Transactions on Signal Processing，2010，58（6）:3042-3054.

［18］ 王燕霞，张弓. 一种改进的用于稀疏表示的正交匹配追踪算法［J］. 信息与电子工程，2012，10（5）:579-583.

［19］ 尚丽，苏品刚，周昌雄，等. 应用轮廓波和稀疏编码收缩法消噪毫米波图像［J］. 计量学报，2012，33（2）:166-170，171.

［20］ 练秋生，张钧芹，陈书贞，等. 基于两级字典与分频带字典的图像超分辨率算法［J］. 自动化学报，2013，39（8）:1310-1320.

［21］ 尚丽，苏品刚，周燕，等. 基于改进的快速稀疏编码的图像特征提取［J］. 计算机应用，2013，33（3）:656-659.

［22］ 浦剑，张军平. 基于词典学习和稀疏表示的超分辨率方法［J］. 模式识别与人工智能，2010，23（3）:335-340.

［23］ 李映，龚红丽，梁佳熙，等. 基于KSVD和PCA的SAR图像目标特征提取［J］. 吉林大学学报（工学版），2010，40（5）:1336-1339.

［24］ 尚丽，苏品刚，周昌雄，等. 轮廓波和非负稀疏编码收缩的毫米波图像恢复［J］. 激光与红外，2011，41（9）:1049-1053.

［25］ 王 蕊，尹忠科，龙 奕，等. 基于改进轮廓波变换的图像去噪算法［J］. 计算机工程，2009，35（6）:228-230.

［26］ SHANG Li，LIU Tao，SUN Zhan li，et al.Image super-resolution reconstruction utilizing the combined method of K-SVD and RAMP ［C］// Lecture Notes in Computer Science （LNCS），Berlin:Heidelberg Springer-Verlag，2014:466-472.

［27］ 孟飞，杨小冈，孙鹏，等. 基于RBF神经网络的激光雷达图像滤波融合算法［J］. 激光与红外，2008，38（6）:616-618.

［28］ 尚丽，苏品刚，陈杰，等. 基于模糊径向基神经网络和稀疏表示的毫米波图像恢复［J］. 计算机应用，2012，32（7）:1871-1874..

［29］ DONG W S，SHI G M，ZHANG L，et al.Super-resolution with nonlocal regularized sparse representation ［C］// Processings of the 2010 SPIE Conference on Visual Communication and Image Processing.Huangshan:IEEE Press，2010:1-10.

［30］ 徐梦溪，徐枫，黄陈蓉，等. 优化最小求解的广义总变分图像复原［J］. 中国图像图形学报，2011，16（7）:1317-1325.

［31］ DONG M K，JIANG A M，SUN J，et al.Dictionary learning based image denoising method using information fusion of residuals ［J］. Microprocessors，2015（1）:58-62.

［32］ DO M N，VETTERLI M.Contourlet:a directional multiresolution image representation ［C］//In the Processing of 9th IEEE International Conference on Image Processing.New York:IEEE Press，2002:357-360.

［33］尚丽，苏品刚. 模拟视觉系统的非负稀疏编码神经网络模型［J］. 苏州市职业大学学报，2014，25（1）:2-11.

［34］ 尚丽，杜吉祥，翟传敏. 稀疏编码算法概述［J］. 苏州市职业大学学报，2009，20（1）:5-10.

（责任编辑:李 华）

Image Restoration Methods Based on Sparse Representation

SHANG Li，LIU Tao，CHEN Jie，HU Zhi-feng
（School of Electronic Information Engineering，Suzhou Vocational University，Suzhou 215104，China）

Sparse representation algorithm based on over-complete dictionary can describe images' inner structure and prior properties and realize the optimized approximation so as to be widely used in image processing. However， in order to obtain higher effect of image reconstruction， we still have some key problems to solve in sparse representation， such as the construction of dictionary models，the optimized sparse decomposition， the convergent speed of algorithms， the estimation of noise models， the linearly inseparability of low dimensional data and so on. So， some image restoration methods based on sparse representation are discussed here， and some relevant research results are of theoretical and practical significance.

sparse representation；dictionary learning；over-complete dictionary；image feature extraction；image restoration

TN911.73

A

1008-5475（2016）03-0002-14

10.16219/j.cnki.szxbzk.2016.03.001

2016-04-29；

2016-05-19

国家自然科学基金资助项目（61373098）

尚 丽（1972-），女，安徽砀山人，教授，博士，主要从事人工神经网络、模式识别、数字图像处理研究.

尚丽，刘韬，陈杰，等.基于稀疏表示的图像恢复方法［J］.苏州市职业大学学报，2016，27（3）：2-15.