黑箱函数优化问题中的一种新型的变形函数策略
2016-10-12齐静
齐 静
(重庆师范大学涉外商贸学院 数学与计算机学院, 重庆 401520)
黑箱函数优化问题中的一种新型的变形函数策略
齐静
(重庆师范大学涉外商贸学院 数学与计算机学院, 重庆 401520)
针对径向基函数插值方法, 提出了一种新的变形函数策略改进径向基的优化效果. 通过数值算例说明了采用这种新构造的变形函数策略在迭代次数上的优越性.
高价黑箱函数; 全局优化; 径向基函数; 响应面模型; 变形函数策略
0 引言
本文采用文献[1]中的径向基函数模型.
给定n个不同的点x1,x2,…,xn∈Rd, 并且它们的函数值f(x1),f(x2),…,f(xn)也是已知的,取定径向基函数φ,构建径向基函数模型
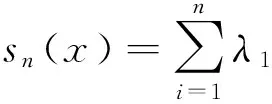
其中,f是一个确定性的连续函数, ‖x-xi‖表示x与中心点xi之间的欧氏距离,λi∈R,i=1,2,…,n,φ为径向基函数.选定一个径向基函数φ之后, 定义矩阵
Φij:=φ(‖xi-xj‖),i,j=1,2,…,n.
1 变形函数策略
根据已选好的初始点x1,x2,…,xn及其函数值f(x1),f(x2),…,f(xn)构建响应面模型,但是我们发现f(x1),f(x2),…,f(xn)中,有些函数值可能非常小,而有些函数值却可能非常大,这些极端的函数值会对构建响应面的精确度造成较大的影响,从而造成较大的误差.为了解决这个问题, 笔者曾提出过一种变形函数策略,用g(f)来替换f,下面通过数值算例说明这种变形函数策略的优越性.
例1已知函数
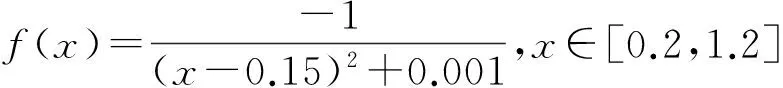
由初始点所构建的径向基响应面为:sn(x)=(158 715 359 558 193log(((50x-11)^2/2 500)^(1/2))(50x-11)^2)/8 589 934 592 000 - (4 512 001 768 305 671log((x^2 -x+ 1/4)^(1/2))(x^2 -x+ 1/4))/4 398 046 511 104 - (401 859 619 198 365 3log(((20x- 1)^2/400)^(1/2))(20x- 1)^2)/219 902 325 555 200-(3 990 528 113 443 431x)/8 796 093 022 208 + (706 589 093 003 557log(((100x- 9)^2/10 000)^(1/2))(100x- 9)^2)/85 899 345 920 000 - (5 269 645 423 418 079log(((100x- 11)^2/10 000)^(1/2))(100x- 11)^2)/687 194 767 360 000 - (1 492 274 980 073 251log(((100x- 19)^2/10 000)^(1/2))(100x- 19)^2)/343 597 383 680 000 + 7 367 518 265 930 379/70 368 744 177 664.
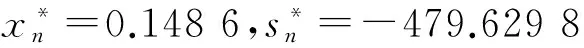
初次构建的响应面模型和原函数的图像如图1所示, 在最优值处构建的响应面模型和原函数的图像如图2所示.
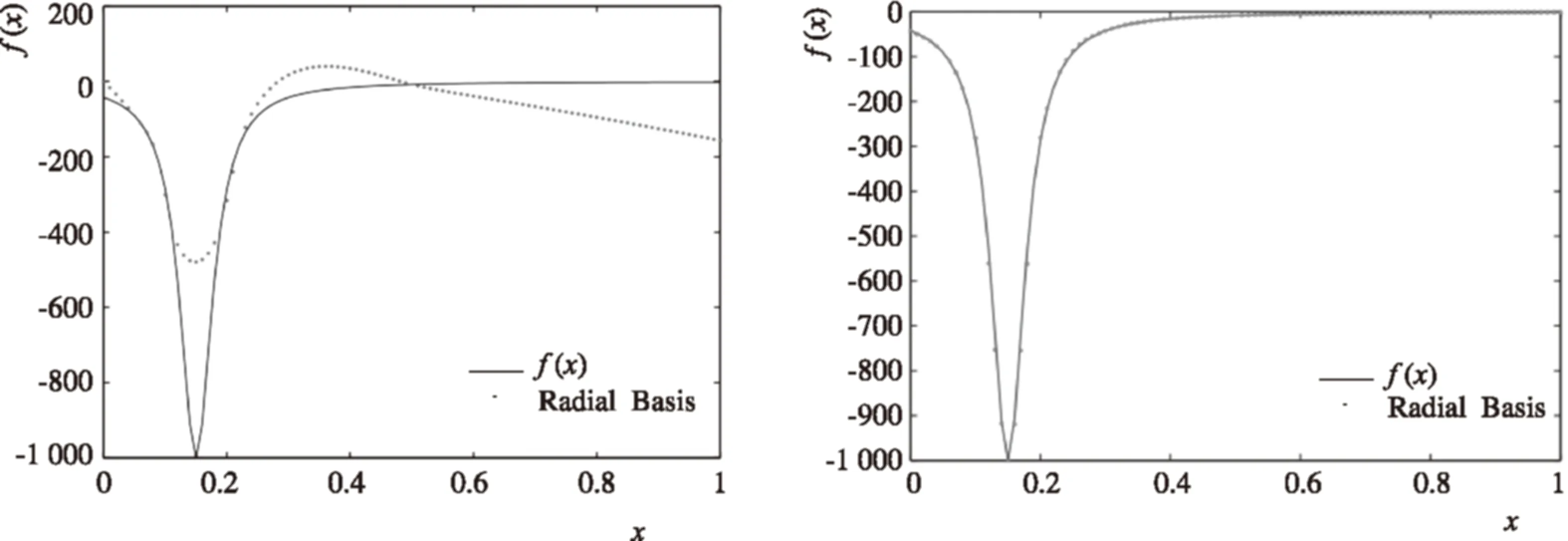
图1初次构建的响应面模型和原函数图像图2最优值处的响应面模型和原函数图像
Fig.1The response sruface model and the original image building for the first timeFig.2The optimal value of the response surface model and the original image
随机选取初始点,当迭代点个数n=30时,尚未达到最优值,所得数据如表1所示.
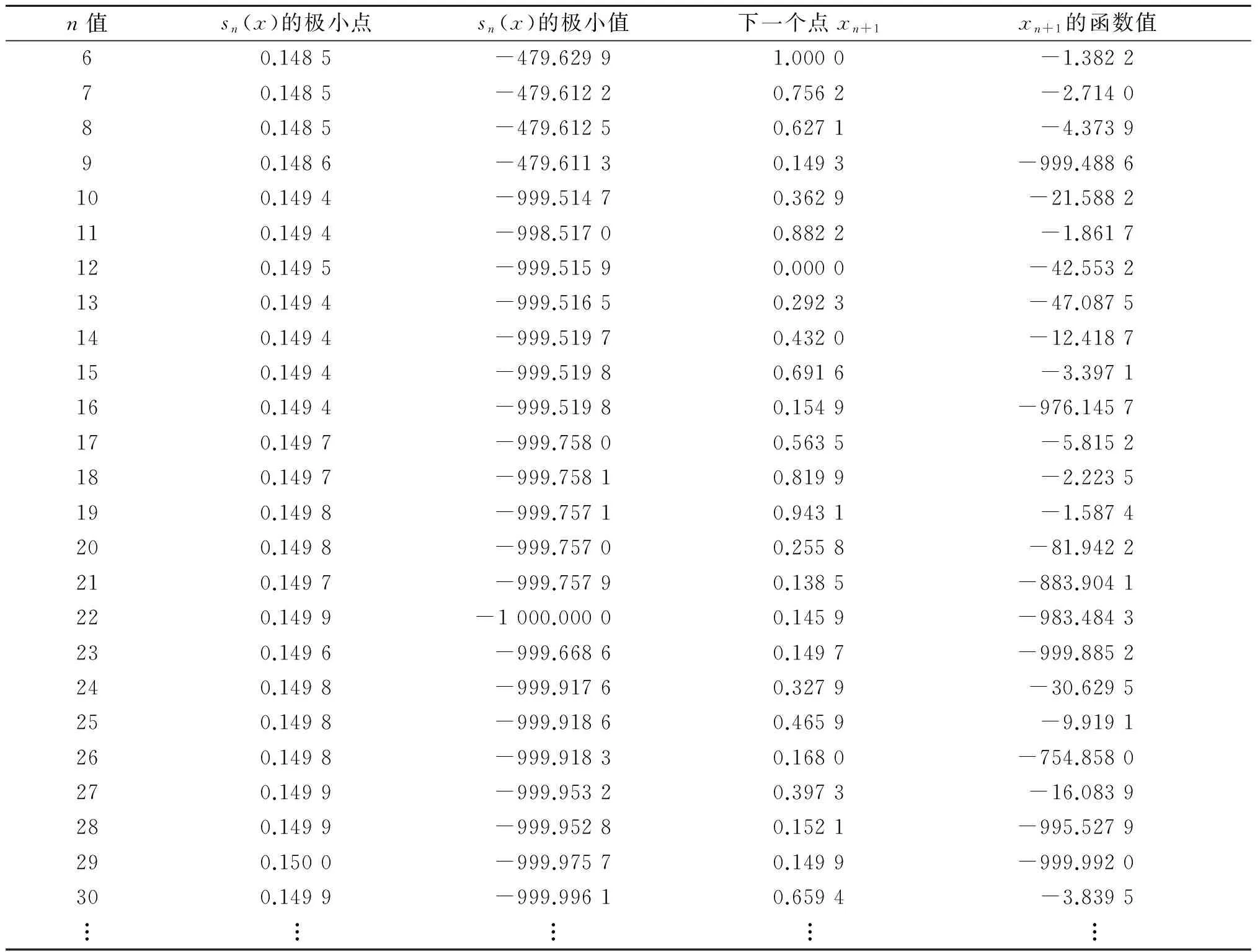
表1 随机选取初始点,当n=30时的数据
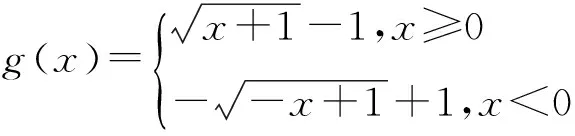
即
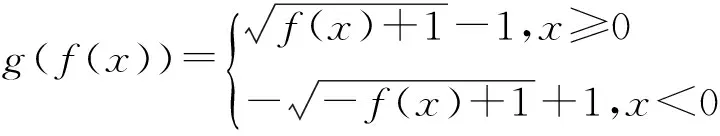
变形函数的初始点也是Gutmann所选的初始点为(0.05,-90.91),(0.09,-217.39),(0.11,-384.62),(0.19,-384.62),(0.22,-169.49),(0.5,-8.10).径向基函数为Φ=r2log(r).
采用本文构造的变形函数策略,当n=11时达到最优值点,迭代次数为11-6=5(次),所得数据如表2所示.分析表2数据可知,采用变形函数策略,达到最优值所需的迭代次数为11-6=5(次),显然采用变形函数方法,可以减少迭代次数,优化迭代过程.
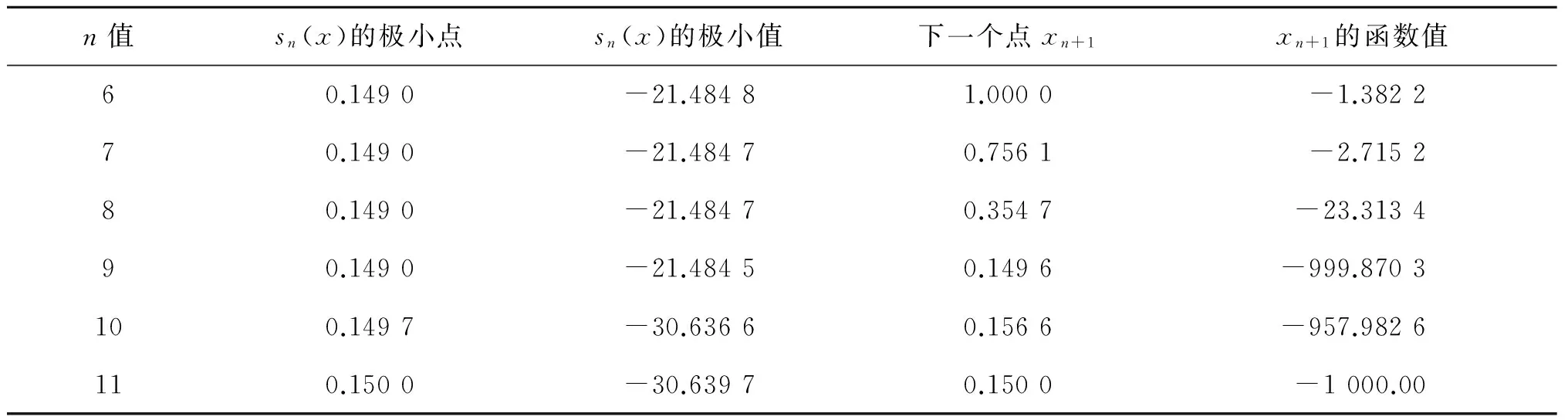
表2 采用本文构造的变形函数策略达到最优值的数据
使用与不使用本文的变形函数策略,达到最优值的迭代次数对比图如图3和图4所示.
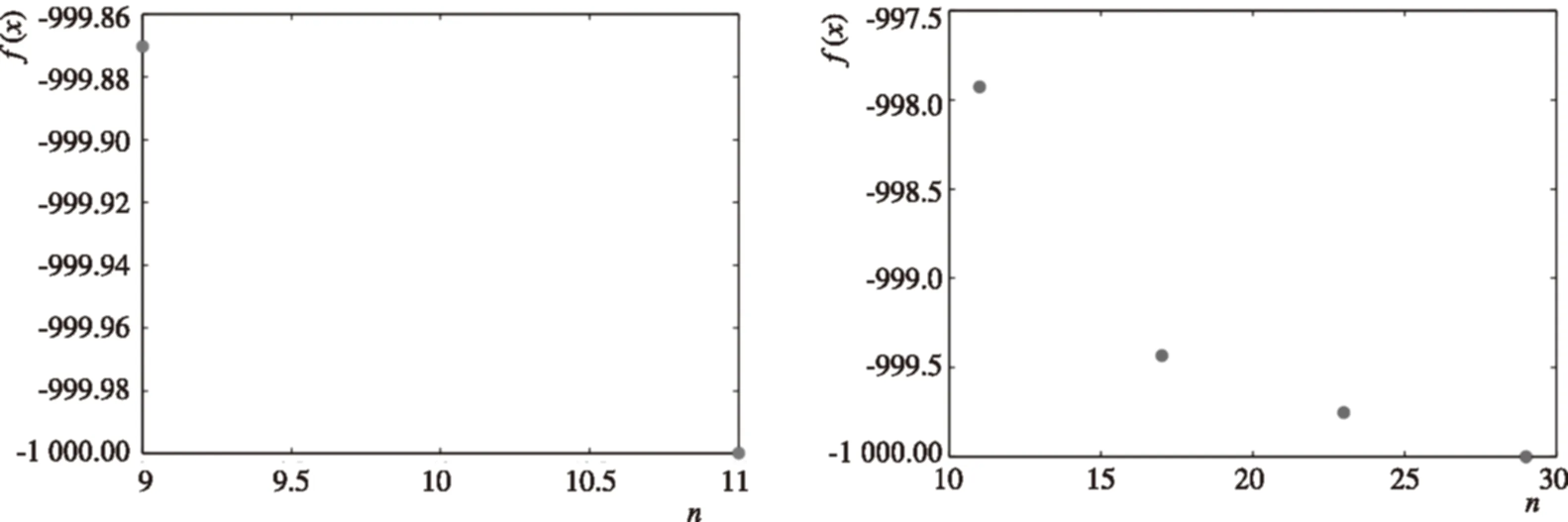
图3使用本文构造的变形函数达到最优值的迭代次数图4不采用本文构造的变形函数达到最优值的迭代次数
Fig.3The numbers of iterations using deformation function constructed in this paper Fig.4The numbers of iterations without deformation function strategy constructed in this paper
构造变形函数后, 达到最优值所需的迭代次数为11-6=5(次); 不采用变形函数, 迭代次数为30-6=24(次),尚未达到最优值. 非常显然, 采用变形函数对一些测试函数来说, 可以减少迭代次数.
下面比较本文构造的变形函数策略与文献[2]中的变形函数策略达到最优值所需的迭代次数.
文献[2]中的变形函数策略为
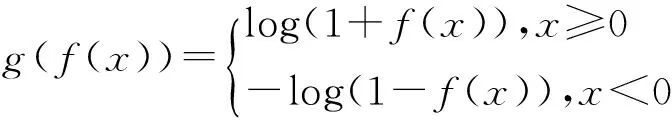
初始点仍为(0.05,-90.91),(0.09,-217.39),(0.11,-384.62),(0.19,-384.62),(0.22,-169.49),(0.5,-8.10).径向基函数为
Φ=r2log(r).
采用文献[2]中的变形函数策略,当n=17时达到最优值点,迭代次数为17-6=11(次),所得数据如表3所示.分析表3的数据可知,文献[2]的变形函数策略, 达到最优值所需迭代的次数为17-6=11(次)(图5).而使用本文的变形函数策略,到达最优值所需迭代的次数为11-6=5(次).很明显,使用本文的变形函数策略可以减少迭代次数,优化迭代过程.
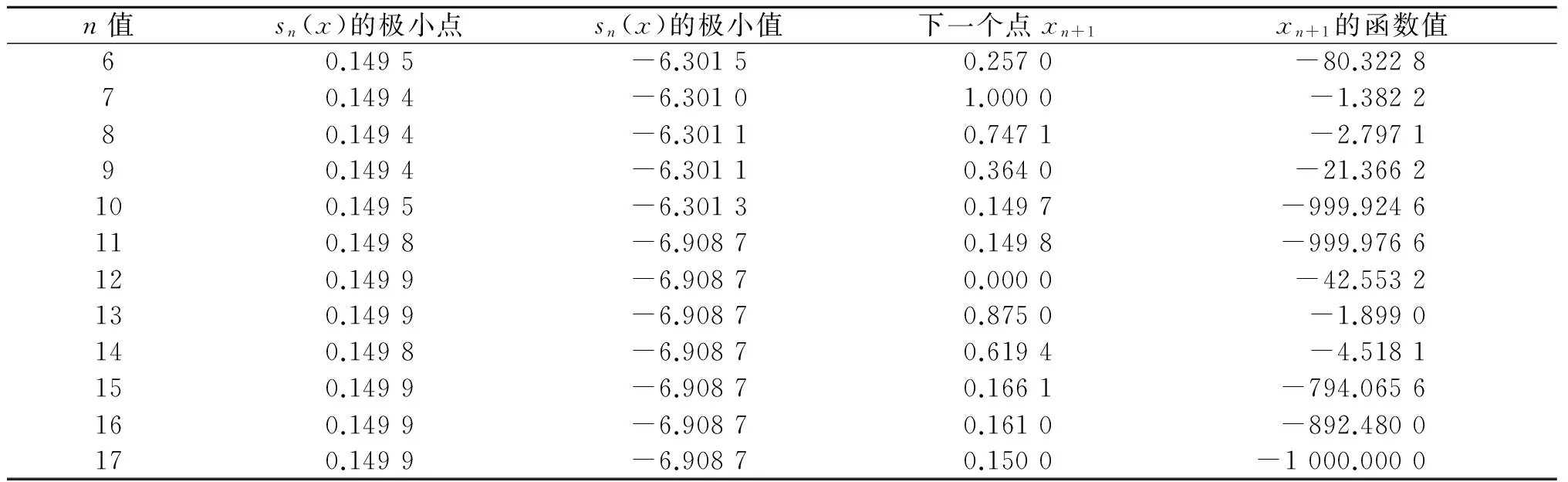
表3 采用文献[2]构造的变形函数策略达到最优值的数据
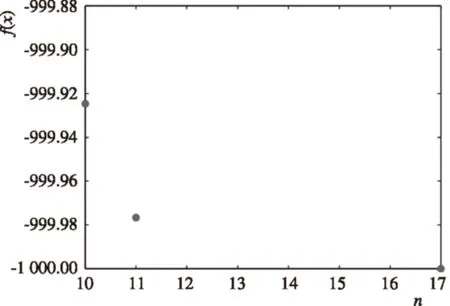
图5 采用文献[2]的变形函数策略达到最优值所需迭代的次数
由以上数据分析可知,采用本文的变形函数策略,在一定程度上可以减少迭代的次数,从而节约时间、节约成本、优化迭代过程.因此在实际优化过程中,通常使用变形函数策略来优化那些过大或者过小的函数值,从而构建较为精确的响应面模型,产生较好的优化效果.
2 小结
径向基函数具有良好的逼近能力及较快的收敛速度[3],使用g(f)来替换f使得构建的响应面更加准确,更有效地进行搜索.因此,径向基函数插值非常适合求解高价黑箱函数的全局最优化问题.
[1]REGIS R G, SHOEMAKER C A. Constrained global optimization of expensive black box function using radial basis function [J]. Journal of Global Optimization, 2005, 31:153-171.
[2]REGIS R G,SHOEMAKER C A. A quasi-multistart framework for global optimization of expensive function using response surface models [J]. Journal of Global Optimization, 2013, 56:1719-1753.
[3]吴宗敏. 函数的径向基表示[J].数学进展,1998, 27(3): 202-208.
A New Type of Deformation Function Strategy for Black Box Function Optimization Problems
QI Jing
(School of Mathematics and Computer Science, Chongqing Normal University Foreign Trade andBusinessCollege,Chongqing401520,China)
A new deformation function strategy to improve the optimization effect of the radial basis function interpolation method was proposed. The advantages of the new deformation function strategy method were illustrated by some numerical examples.
expensive black box function; global optimization; radial basis function; response surface model; deformation function strategy
2016-07-01
齐静(1990—),女,河南南阳人,重庆师范大学涉外商贸学院数学与计算机学院教师.
10.3969/j.issn.1007-0834.2016.03.007
O241.6
A
1007-0834(2016)03-0023-04
