Newton公式的一个注记及其应用
2016-10-12顾江永
顾江永
(宿迁学院 文理学院,江苏 宿迁 223800)
Newton公式的一个注记及其应用
顾江永
(宿迁学院 文理学院,江苏 宿迁 223800)
通过对Newton公式的研究,得出了一个较为简洁的结论,并利用该结论对Newton公式进行等价的证明;同时举例说明结论的相关应用.
Newton公式;推广;应用
Newton公式在组合数学、数值计算、方程求根等方面有着重要的作用,它给出了一元n次多项式根的次幂之和与多项式系数之间的相互关系.沈南山在文献[1]中对Newton公式的条件进行了推广,使两个结论得到了统一.本文从次幂和的角度对Newton公式进行推广,给出了一个较为简洁且直观的结论.
引理已知复数域上的一元多项式
fn(x)=xn+a1xn-1+a2xn-2+…+an-1x+an,

证明设fm(x)=xm+a1xm-1+a2xm-2+…+am-1x+am的m个复根分别为y1,y2,…,ym,则
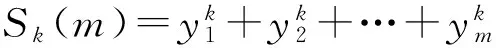
因为Sk(n)和Sk(m)都是对称多项式,所以根据对称多项式基本定理[2],它们可以表示为初等对称多项式的多项式.
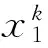

表1 指数方幂表
设

(1)
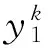

(2)
根据Vieta定理[4],知σi=(-1)iai,i=1,2,…,k,所以(1)与(2)式中的σi都相同.
令(y1,y2,…,ym)=(x1,x2,…,xn,0,0,…,0)=(c1,c2,…,cn,0,0,…,0),c1,c2,…,cn为任意常数,代入(1)与(2)式得,bi=ci,(i=1,2,…,t),所以Sk(n)=Sk(m),(1≤k≤n).
推论[1]复数域上的多项式
f(x)=a0xn+a1xn-1+a2xn-2+…+an-1x+an,a0≠0,
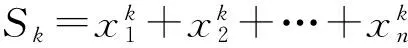
a0Sk+a1Sk-1+a2Sk-2+…+an-1Sk-n+1+anSk-n=0.
Newton公式[4]复数域上的多项式
f(x)=xn+a1xn-1+a2xn-2+…+an-1x+an,

1)当k≥n时,Sk+a1Sk-1+a2Sk-2+…+an-1Sk-n+1+anSk-n=0;
2)当1≤k≤n时,Sk+a1Sk-1+a2Sk-2+…+ak-1S1+kak=0.
证明构造多项式
f(x,x1,x2,…,xn)=(x-x1)(x-x2)…(x-xn),
将其展开,得
f(x,x1,x2,…,xn)=xn-σ1xn-1+σ2xn-2+…+(-1)n-1σn-1x+(-1)nσn.
由韦达定理,可得
f(x,x1,x2,…,xn)=xn+a1xn-1+a2xn-2+…+an-1x+an.
令x=x1,x2,…,xn,分别代入多项式
f(x,x1,x2,…,xn)=(x-x1)(x-x2)…(x-xn),
得
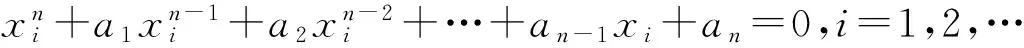
1)当k≥n时,上式两边同时乘以xik-n,i=1,2,…,n,得

这n个等式相加,得k≥n时的Newton公式
Sk+a1Sk-1+a2Sk-2+…+an-1Sk-n+1+anSk-n=0.
2)当1≤k≤n时,由推论直接可得
Sk+a1Sk-1+a2Sk-2+…+ak-1S1+kak=0.
下面给出公式的两个应用.


(1)
k=1,2,…,n.
证明利用第二数学归纳法.
当k=1时,根据Vieta定理[5]知,a1=x1+x2+…+xn=S1,结论成立.
假设当k≤n时结论成立,下证当k=n时的情形.由Newton公式可知,只要证明行列式中Sk(k)成立即可.把式(1)右端行列式按最后一行展开并结合Newton公式,得
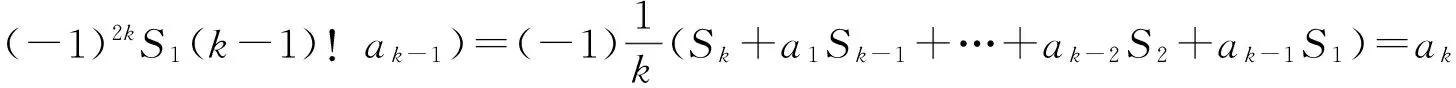
根据第二数学归纳法原理,对任意的自然数k,结论都成立.

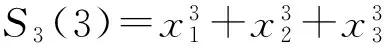

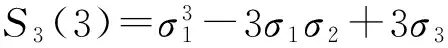
又因为σ1=-2,σ2=3,σ3=-4,所以
S3(7)=S3(3)=(-2)3-3×(-2)×(-3)+3×(-4)=-2.
[1]沈南山.牛顿(Newton)公式的一个注记及其应用[J].数学通报,2005(3):38-39.
[2]北京大学数学系.高等代数[M]. 北京: 高等教育出版社,2003:42-49.
[3]徐仲,陆全. 高等代数考研教案[M].2版.西安: 西北工业大学出版社,2009:39-40.
[4]南秀全. 多项式[M]. 武汉: 湖北教育出版社,2002: 209-213.
[5]潘有发. 韦达定理史话[J]. 学生之友(初中版),2003(11):44-45.
A Note on Newton Formula and Its Applications
GU Jiangyong
(Department of Arts and Science, Suqian College, Suqian 223800, China)
A more concise corollary is given by the study of the Newton formula. And by this conclusion, the Newton formula is proved to be equivalent. The relevant applications of the results are reflected by giving examples.
Newton formula; corollary; application
2016-04-12
宿迁学院科研基金(SQXY201506)
顾江永(1977—),男,江苏宿迁人,宿迁学院文理学院副教授,主要研究方向:代数学.
10.3969/j.issn.1007-0834.2016.03.002
O151.1
A
1007-0834(2016)03-0004-03
