纵向数据与生存数据联合模型中多变点识别问题

沈 佳 坤，　宋 立 新，　孙 秀 峰，　冯 宝 军

( 1.大连理工大学 管理与经济学部, 辽宁 大连　116024；2.大连理工大学 数学科学学院, 辽宁 大连　116024 )



纵向数据与生存数据联合模型中多变点识别问题

沈 佳 坤1,2，宋 立 新*2，孙 秀 峰1，冯 宝 军1

( 1.大连理工大学 管理与经济学部, 辽宁 大连116024；2.大连理工大学 数学科学学院, 辽宁 大连116024 )

提出了共享协变量和随机效应的纵向响应中含有多个变点识别的线性混合效应(LME)模型和加速失效时间(AFT)模型的联合模型，并通过Gauss-Hermite近似解决极大似然函数中的复杂积分以得到参数的估计．通过模拟研究验证了该方法的有效性，并将其应用于原发性胆汁性肝硬化(PBC)病变过程，研究发现：PBC患者的血清胆红素只在初期治疗阶段有所降低，两个月之后迅速开始反弹，直到3.5 a后增速才有所放缓，说明治疗方法仍需改进．

多变点；线性混合效应模型；加速失效时间模型；联合推断；极大似然

0　引　言

纵向数据既包含横截面数据中多个体间的对比差异，又包含时间序列数据中对个体重复测量的变化趋势，能较好地反映研究对象的动态变化特征，常被用来评定诱导危害人们身体健康的风险因素的影响、描述患者的生活改善以及评估治疗的效率．此外，生存分析揭示了患者从开始治疗到疾病复发或患者死亡等重要临床事件的时间变化规律，是医学统计研究中的另一个重要内容，已取得了很多成果．然而，当纵向响应回归模型与失效时间回归模型之间存在某种相关关系时，如体现在一些共同的潜在过程或协变量上，分别独立地进行纵向数据和生存分析研究会导致结果产生偏差．综上，为了将所有影响研究结果的信息都利用起来得到无偏估计结果，建立纵向响应和生存时间的联合模型势在必行，并已得到学界的普遍认同[1-2]．

在实际研究中，患者的病情随时间的发展往往不是单纯的线性关系，而是呈现出阶段性的变化特点．为此，学者们一直在努力寻找更简洁、合理的非线性模型来描述患者病情变化，其中变点回归以其简洁的形式、较好的拟合度且具有在变点处连续的良好性质而深受学者们的喜爱，被较多地应用于病情变化波动大的流行病学和癌症研究中，来识别疾病发展过程中医学指标变化规律发生改变的时间点[3-6]．最近，Huang等[7]提出了两个变点的分段线性模型，并通过贝叶斯的方法得到变点的分布，来描述HIV病毒载量随时间的变化情况．但由于贝叶斯方法过于依赖给定的先验分布，不能准确反映新情况下响应变量的自然变化规律，导致了研究结果的局限性．

本研究将极大似然估计法引入分段线性模型，以克服贝叶斯推断固有的缺点，服务于临床管理中病人用药的指导服务及医疗决策中肝移植时机的选择等．

1　模型和方法

1.1联合模型

考虑一个样本量为N的样本，个体间相互独立．令Yij为个体i在时间tij的响应变量，j=1,…,ni且i=1,…,N．本文建立关于纵向数据的含有k个变点的线性混合效应(LME)模型(1)，其中k为任意正整数，并将k个变点在时间轴上的位置作为未知参数：τ=(τ1τ2…τk)．

Δi1(tij-τ1)++Δi2(tij-τ2)++…+

Δik(tij-τk)++eij

(1)

其中Δi1=(μ3+ui3)-(μ2+ui2)，Δi2=(μ4+ui4)-(μ3+ui3)，…，Δik=(μk+2+uik+2)-(μk+1+uik+1)；τ1<τ2，…，<τk，j=1，…，ni，i=1，…，N，k≥1．

令Ti是个体i的生存时间，在临床实际中，它往往与个体i的纵向数据模型(1)有关．为体现这种关联性，研究中假设生存数据模型与纵向数据模型(1)共享协变量向量Zi和随机效应向量ui．特别的，建立混合效应加速失效时间(AFT)模型(2)：

(2)

1.2变点识别

在确定纵向数据模型变点个数阶段，本文提出一系列模型的假设检验，利用似然比检验(LRT)的方法确定LME模型(1)中的变点个数，使得联合模型对样本的拟合度达到相对最优．

然后，本文通过LRT方法确定变点个数，寻找使联合模型具有最优拟合度的相应纵向数据分段LME模型．第k组LRT方法中检验统计量LR(k)的定义如下式所示：

LR(k)=

-2[l(k)0(θ^(k)0)-l(k)1(θ^1(k))]～·

(3)

θ^(k)0

θ^(k)1

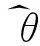
1.3联合似然推断

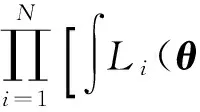
(4)

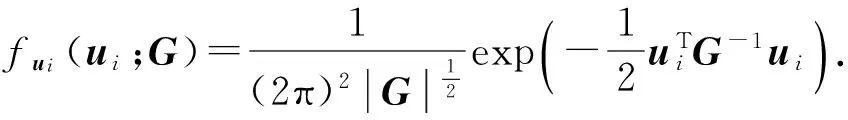
fTi，δi|Zi，ui(ti，δi|Zi，ui;γ，σ2)fui(ui;G)]dui=

fTi，δi|Zi，ui(ti，δi|Zi，ui;γ，σ2)fui(ui;G)dui=

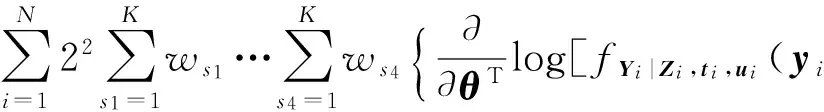
(5)

式中：K为正交节点的个数；us=(us1…us4)T，是节点值，相应的权重为ws=(ws1…ws4)T．当被积函数可以被写作exp(-uTu)l(u)的形式时，合理设置节点值和相应权重可以得到积分较为准确的估计，其中l(u)为阶数小于等于K-1的关于u的多项式，即当节点数K足够大时，近似方程(5)可以无限接近积分的准确值．从而，本文建立的联合模型的似然推断在积分近似意义下是可解的．

2　数值模拟

2.1模拟方案

不失一般性，本文考虑含有一个随机效应项和两个变点的LME模型：

Yij=(μ0+ui)+μ1Zi+μ2tij+(μ3-μ2)×

(tij-τ1)++(μ4-μ3)(tij-τ2)++eij

(6)

其中τ1<τ2，j=1，…，ni，i=1，…，N．

相应的生存分析，建立混合效应AFT模型(7)．生存时间Ti满足1．3节中的右删失假设．

logTi=γ0+γ1Zi+γ2ui+i，

(7)

下面通过一系列数值模拟研究来验证上一章中提出的联合模型及估计方法的有效性．本节的数值模拟基于共享的Z和u的联合模型(6)和(7)．假设样本容量为N=150或N=300，个体间相互独立，每个个体的重复观测次数为ni=6或ni=10．令υ2=σ2=0.12，μ=(0.2-0.3-0.80.90.2)T，且G=0.452．

当ni=6时，为获得个体i的重复观测时间，本研究从均匀分布U(0，6)无放回随机抽取的6个时间点得到次序统计量ti，并建立生存时间的右删失示性函数δi=I(Ti≤ti6)，其中ti6是上述抽取均匀分布时间点的最大次序统计量，假设变点τ=(13)，且参数γ=(1.20.50.2)T；当ni=10时，同理，本文从均匀分布U(0，10)无放回随机抽取的10个时间点得到次序统计量ti，并建立生存时间的右删失示性函数δi=I(Ti≤ti10)，其中ti10是上述抽取均匀分布时间点的最大次序统计量，假设变点τ=(48)，参数γ=(1．80.50.2)T．同时，假设Zi服从二项分布B(1，0.5)．

从而形成4组纵向数据和生存数据的数值模拟方案：

(a)个体数为150，每个个体重复观测次数为6；

(b)个体数为150，每个个体重复观测次数为10；

(c)个体数为300，每个个体重复观测次数为6；

(d)个体数为300，每个个体重复观测次数为10．

2.2数值结果

一般的，本研究选择最大观测时间的1/3以及2/3分位数作为极大似然方法估计两个变点位置的初值，以上4组纵向数据和生存数据分别作100次数值模拟．将4种模拟方案下变点(τ1τ2)的估计结果列示于表1．

表1中的偏差和均方误差都比原值小4个数量级以上，表明在该4种数值模拟方案情形下，极大似然方法可以几乎准确估计到变点的位置．

表2列示了4种数值模拟情形下联合模型的参数估计优度相关结果．

通过表2中的普遍低于参数值本身1～3个数量级不等的偏差和均方误差可以验证参数估计的无偏性和有效性．此外，注意到偏差和均方误差随着重复测量次数ni由6到10或样本量N由150到300的增加而降低．

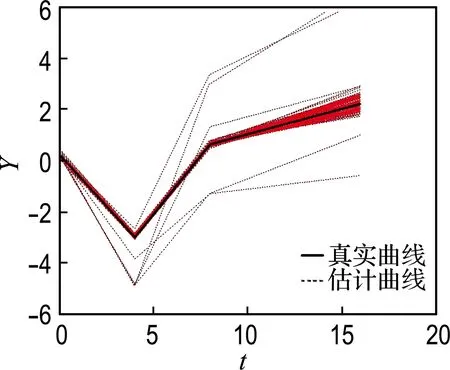
图1更直观地呈现了4种方案的数值模拟，各100次实验的估计曲线结果，其中实线表示真实曲线，虚线表示估计曲线．

由图1中的曲线可以明显看出重复测量次数ni由6(图(a)和(c))到10(图(b)和(d))，估计曲线与真实曲线之间的差异减小；样本量N由150(图(a)和(b))到300(图(c)和(d))，估计曲线与真实曲线之间的差异明显减小．

表1　两个变点位置的数值模拟结果

表2　联合模型数值模拟的参数估计结果

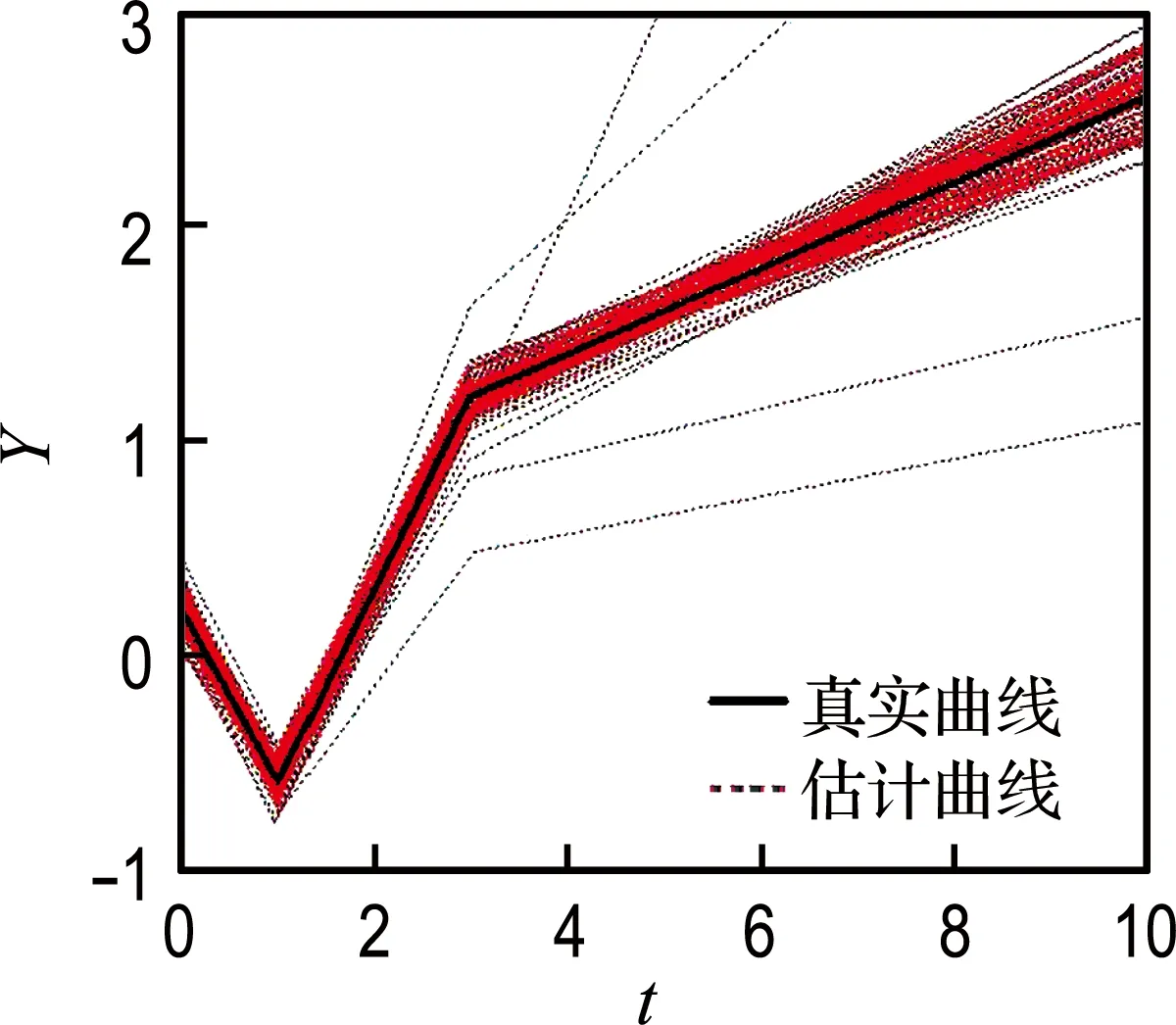
　　(a)方案(a)

(b) 方案(b)

(c) 方案(c)

(d) 方案(d)

图14种方案模拟研究曲线

Fig.1The simulation curves of four strategies

3　原发性胆汁性肝硬化(PBC)实例分析

本文使用的PBC数据集来自于美国梅约(Mayo)医学研究中心1974年到1984年采集的患者资料[9]，包括312名随机选取的独立患者，其中158名患者使用D-青霉胺(D-penicillamine)治疗(占51%)，其他154名使用安慰剂(placebo)治疗(占49%)．该数据集包括患者的基本信息，如年龄、性别等及一些跟踪测量的生物病理指标，如血清胆红素(serum bilirubin)、皮肤血管畸形、肝脏肿大等[10]．本文研究的兴趣在于反映PBC症进程的血清胆红素在不同治疗方式下的变化情况，以及相应的生存时间(即从开始治疗到死亡或肝移植的时间)的变化特征．

上述美国梅约医学研究中心PBC数据组，跟踪记录的312名随机选取的患者的情况，包含20个变量，各1 945个观测值，可以在R语言的JM包中直接获得．本研究主要关注如下观测变量：Y代表血清胆红素serBilir(mg/dL)，是检测原发性胆汁性肝硬化程度的指标；t定义为登记日到每次观测年数year；Z是用药情况drug，用药选择为D-青霉胺或安慰剂；T定义为登记日到换肝、死亡或研究分析时间的年数years；δ是生存时间的右删失示性函数status2，取值为1时表示患者换肝或死亡，取值为0时表示患者治愈．

本文对这组实例数据的分析将分三步进行：(1)确定纵向数据模型的变点个数；(2)估计变点在时间轴上的位置；(3)选择建立联合模型得到相应的参数估计．

首先，确定纵向数据多变点LME模型中变点的个数．对于样本量为N的患者间相互独立的样本，令Yij为患者i在时间tij的血清胆红素的测量值．通过1．2节中假设检验规则，通过原假设和备择假设中的纵向数据模型，建立一系列关于PBC数据组的联合模型JM0，JM1，…，JMk，检验结果如表3所示．

由表3知，在超过99.99%的置信度水平上含有1个变点的联合模型JM1对PBC 数据的拟合度优于没有变点的联合模型JM0；在超过99.99% 的置信度水平上含有2个变点的联合模型JM2对数据的拟合度优于含有1个变点的联合模型JM1；含有3个变点的联合模型JM3对数据的拟合度不显著优于含有2个变点的联合模型JM2．从而含有2个变点的LME模型和相应混合效应AFT模型构成的联合模型JM2在本研究中对PBC数据拟合最优，且AIC和BIC结果也都支持了该结论．

表3　PBC联合模型似然比检验结果

然后，本文选用如下纵向数据模型(8)和生存时间模型(9)通过共享协变量Zi和随机效应向量ui构成联合模型描述PBC数据．

logYij=(μ0+ui1)+μ1Zi+(μ2+ui2)tij+Δi1(tij-τ1)++Δi2(tij-τ2)++eij

(8)

(9)

其中Zi是有两个取值的等级协变量，Ti是患者i从登记日到死亡、肝移植或研究分析时间的年数，相应的生存时间的右删失示性函数为δi，参数向量γ2与随机效应向量ui的维数一致．

同上一章模拟研究一样，本研究选观测时间变量t最大值的1/3和2/3分位数即0.988 4和3.983 7，作为极大似然优化方法估计两个变点位置的初值．通过计算可以得到两个变点在时间轴上的位置(τ1τ2)为(0.141 53.542 2)，即为登记日起的第2个月和第3.5 a．

最后，通过Gauss-Hermite近似意义下的极大似然方法得到联合模型中其他参数的估计值及标准误，如表4所示．

表4　PBC联合模型参数估计

由表4可知，用药Z的系数为-0.306 9，说明D-青霉胺确实对血清胆红素的升高有抑制作用．通过时间进程的参数估计及上述两个变点的估计值可知，从开始用药到第2个月为第一阶段，该阶段的血清胆红素有一个短暂而明显的降低，增长率为-0.694 7，标准误较大为0.212 4，并且相应随机效应的方差估计值也较大为4.416 4，说明由于用药的不同，这一阶段不同个体的血清胆红素变化差异加大；接着很快开始反弹，血清胆红素呈现正向增长，增长率为0.172 8，标准误较小为0.019 0，并且相应随机效应的方差估计值也较小为0.078 9；直到第3.5 a的时候，血清胆红素增速变缓，增长率变为0.130 5直到观测结束，标准误进一步减小为0.013 3，相应随机效应的方差估计值进一步减小为0.021 6，说明随着时间的增加，患者抗药性的增强，个体间的差异逐渐减小．

图2显示了12个随机选择的PBC患者血清胆红素观测值及拟合曲线．

图212个随机选择的PBC患者血清胆红素观测值及拟合曲线

Fig.2TheobservedvaluesandsimulationcurvesofserBilirfor12randomlyselectedPBCpatients

图2直观地显示了治疗对降低患者的血清胆红素只有一开始产生了较好的效果，持续大概两个月的时间之后开始反弹，直到3.5 a的时候血清胆红素的增速开始放缓，但仍保持增长趋势，说明治疗方法需要改进．

4　结　语

本研究首先对分段LME模型中合适的变点个数进行选择，使得联合模型对纵向及生存数据具有最优拟合度，进而建立了共享协变量和随机效应的含有多个变点的纵向数据LME模型和生存数据AFT模型的联合模型．在此基础上，本研究得到了变点在时间轴上的位置估计值，并通过Gauss-Hermite近似解决了联合似然函数中的复杂积分以得到模型中其他参数的估计，较好地解释了协变量及随机效应对纵向响应变量和生存时间的影响．最后将该模型运用到PBC数据中，研究发现：PBC患者的血清胆红素只在初期治疗阶段有所降低，两个月后迅速开始反弹，直到3.5 a后增速才有所放缓，说明治疗方法仍需改进．

[1]Tsiatis A A, Degruttola V, Wulfsohn M S. Modeling the relationship of survival to longitudinal data measured with error. Applications to survival and CD4 counts in patients with AIDS [J]. Journal of the American Statistical Association, 1995, 90(429):27-37.

[2]Wulfsohn M S, Tsiatis A A. A joint model for survival and longitudinal data measured with error[J]. Biometrics, 1997, 53(1):330-339.

[3]Hinkley D V. Inference about the change-point in a sequence of random variables[J]. Biometrika, 1970, 57(1):1-17.

[4]Smith A F M, Cook D G. Straight lines with a change-point:a Bayesian analysis of some renal transplant data [J]. Applied Statistics, 1980, 29(2):180-189.

[5]Kim H M, Lagakos S W. Assessing drug compliance using longitudinal marker data, with application to AIDS[J]. Statistics in Medicine, 1995, 13(19-20):2141-2153.

[6]Kim H J, Fay M P, Feuer E J,etal. Permutation tests for joinpoint regression with applications to cancer rates[J]. Statistics in Medicine, 2000, 19(3):335-351.

[7]Huang Y, Dagne G A, Park J G. Segmental modeling of changing immunologic response for CD4 data with skewness, missingness and dropout [J]. Journal of Applied Statistics, 2013, 40(10):2244-2258.

[8]Evans M, Swartz T. Approximating Integrals via Monte Carlo and Deterministic Methods [M]. Oxford:Oxford University Press, 2000.

[9]Murtaugh P A, Dickson E R, van Dam G M,etal. Primary biliary cirrhosis:Prediction of short-term survival based on repeated patient visits [J]. Hepatology, 1994, 20(1):126-134.

[10]Shapiro J M, Smith H, Schaffner F. Serum bilirubin:a prognostic factor in primary biliary cirrhosis[J]. Gut, 1979, 20(2):137-140.

Multiple change points identification in joint modeling of longitudinal and survival data

SHENJia-kun1,2,SONGLi-xin*2,SUNXiu-feng1,FENGBao-jun1

( 1.Faculty of Management and Economics, Dalian University of Technology, Dalian 116024, China；2.School of Mathematical Sciences, Dalian University of Technology, Dalian 116024, China )

A joint model with multiple change points identifying in longitudinal response process is proposed, which combines a linear mixed-effect (LME) model and an accelerated failure time (AFT) model with respect to shared covariates and random effects. All the parameters are estimated by the maximum likelihood function through the Gauss-Hermite approximation to deal with the intractable integrals in it. The effect of the method is elucidated through simulation studies and a real data application about primary biliary cirrhosis (PBC). It is shown that serum bilirubin level declines only at the beginning of treatment and lasts two months, then quickly rebounds and doesn′t slow down until 3.5 years later, which indicates that the treatment methods still need to be improved.

multiple change points; linear mixed-effect (LME) model; accelerated failure time (AFT) model; joint inference; maximum likelihood

1000-8608(2016)05-0539-07

2016-01-15；

2016-07-08．

国家社会科学基金资助项目(16BGL060)；国家自然科学基金资助项目(11371077).

沈佳坤(1991-)，女，博士生，E-mail:shenjiakun@mail.dlut.edu.cn；宋立新*(1966-)，男，教授，博士生导师，E-mail:lxsong@dlut.edu.cn；冯宝军(1966-)，男，教授，博士生导师，E-mail:fbj066@sina.com.

O212

A

10.7511/dllgxb201605015