一级气体炮内弹道方程修正及验证

李　锋,拜云山,冯晓伟

(中国工程物理研究院 总体工程研究所,四川 绵阳 621999)



一级气体炮内弹道方程修正及验证

李锋,拜云山,冯晓伟

(中国工程物理研究院 总体工程研究所,四川 绵阳 621999)

为了使理论计算结果更为准确可靠,对一级气体炮内弹道经典方程进行修正。分析了一级气体炮内弹道经典方程存在的问题及原因,指出气室容积不能忽略。提出了气体密度新的表达方式,并根据质量守恒方程、气流动量方程、弹丸运动方程、气体绝热膨胀方程和理想气体状态方程等,联立推导出一级气体炮内弹道修正方程。将修正方程、经典方程计算结果与内弹道流体数值仿真结果进行对比，结果表明:在容积比较小的情况下三者的偏差很小;但随着容积比的增大,经典方程计算结果偏离修正方程和数值仿真计算结果;经典方程仅适用于容积比较小的情况;而修正方程的适用范围不受容积比大小限制,验证了修正方程的正确性和适用性。

气体炮;内弹道;炮口速度;容积比

气体炮作为一种加载试验装置,采用压缩气体作为动力源驱动弹丸运动以获得期望的速度。1946年,美国研制成功第一门利用轻质气体作为工作介质的一级气体炮[1],此后,美国、加拿大、英国和法国以及我国一些单位陆续建立了气体炮装置,使这种类型的弹丸发射装置成为一种使用极其广泛的试验设备。

Pidduck和Kent最早进行了气体炮内弹道方程的研究,提出采用振荡函数近似描述波在弹后的传播规律[2],给出了解析模型。Seigel A E采用数值仿真方法对一级气体炮的气体动力学问题进行了研究,并与Pidduck和Kent的解析模型计算结果进行对比,指出当压缩气体与弹丸质量之比小于1/4时,数值计算结果与Pidduck的解析解非常接近[3]。王金贵借用火炮内弹道理论中虚拟质量系数表达形式,结合气体动力学方程推导了气体炮内弹道方程[4],获得了炮口初速的解析表达式,并在气体炮设计上得到了应用,实际上已成为国内气体炮设计的理论依据,本文称之为经典方程。赵俊利等[5]建立了气体炮内弹道数学模型,给出了与文献[4]相同的内弹道理论公式,在具体参数计算方法上进行了简化。Mark Denny[6]将弹丸附加质量作为常量处理,建立了考虑弹前气压和破膜能量损失影响的内弹道解析模型,该模型在去掉弹前气压和破膜能量损失项后在形式上与经典方程相同。

目前,研究人员在气体炮内弹道方面多针对具体结构型式进行数值仿真。杨均匀等[7]采用Von Neumann Richtmyer差分格式对带有坡膛、有限药室长的一级轻气炮进行了内弹道一维数值模拟。仲伟君等[8]针对四腔结构的气体炮,运用气体动力学的相似理论建立了气体炮的内弹道模型,并在计算机上进行了数值模拟。赵希欣等[9]应用气体动力学理论及配合间隙的影响建立了考虑气体泄露的内弹道模型,并进行了数值仿真分析。胡静等[10]建立了三维非定常条件下35 mm等截面轻气炮数学模型,采用ANSYS-CFX软件对不同气体工质所获弹丸初速进行模拟计算。夏正友[11]采用一种基于推理的神经网络模型,对气体炮内弹道最大膛压进行了仿真和预测。

一级气体炮经典方程针对较为理想的结构型式,借鉴火炮内弹道[12]的相关理论,通过理论分析和推导,获得了炮口初速与内弹道参数的解析表达式,与数值模拟相比在工程应用上更为方便。但由于简化较多,实际应用中发现经典方程在大气室容积的情况下存在一定的局限性。本文分析了经典内弹道方程存在的问题及原因,对炮管内气体密度表达式进行了修正,并推导了新的气体炮内弹道方程,称之为修正方程,进一步将修正方程和经典方程与数值仿真结果进行对比,给出了各自的适用范围,完成了对修正方程的验证。

1　气体炮内弹道经典方程分析

根据一般的一级气体炮结构形式,建立气体炮内弹道物理模型,如图1所示,图中,S为炮管截面积,L为弹丸在膛内的行程,lp为t时刻弹丸在膛内的运动位移。采用如下基本假设:

①气室气体为理想气体,整个发射过程视为理想气体绝热膨胀过程;

②不考虑弹前气体压力的影响;

③不考虑各种损耗的具体形式,在计算过程中引入虚拟质量系数φ来计入能量损失因素,φ的具体形式与火炮内弹道方程相同[4]。

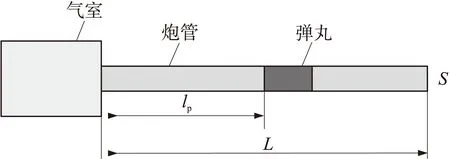
图1　一级气体炮内弹道物理模型

王金贵[4]基于上述假设,通过联立求解理想气体状态方程、气体绝热过程方程、弹丸运动方程等,得到弹丸炮口初速与气室容积、气室压力、炮弹质量、炮管尺寸等的关系:

(1)

式中:vm为弹丸炮口初速,p0为气室初始压力,V0为气室容积,m为弹丸质量,φ为虚拟质量系数,c为绝热指数。

本文称式(1)为一级气体炮内弹道经典方程。根据式(1),炮口初速随气室容积的变化规律如图2所示(炮管直径为80 mm,弹丸行程为1 m,弹丸质量为2 kg,气室压力为5 MPa)。从图2中可以看出,炮口初速随着气室容积的增大先增大后减小,而内弹道数值仿真结果表明炮口初速随着气室容积增大而增大。

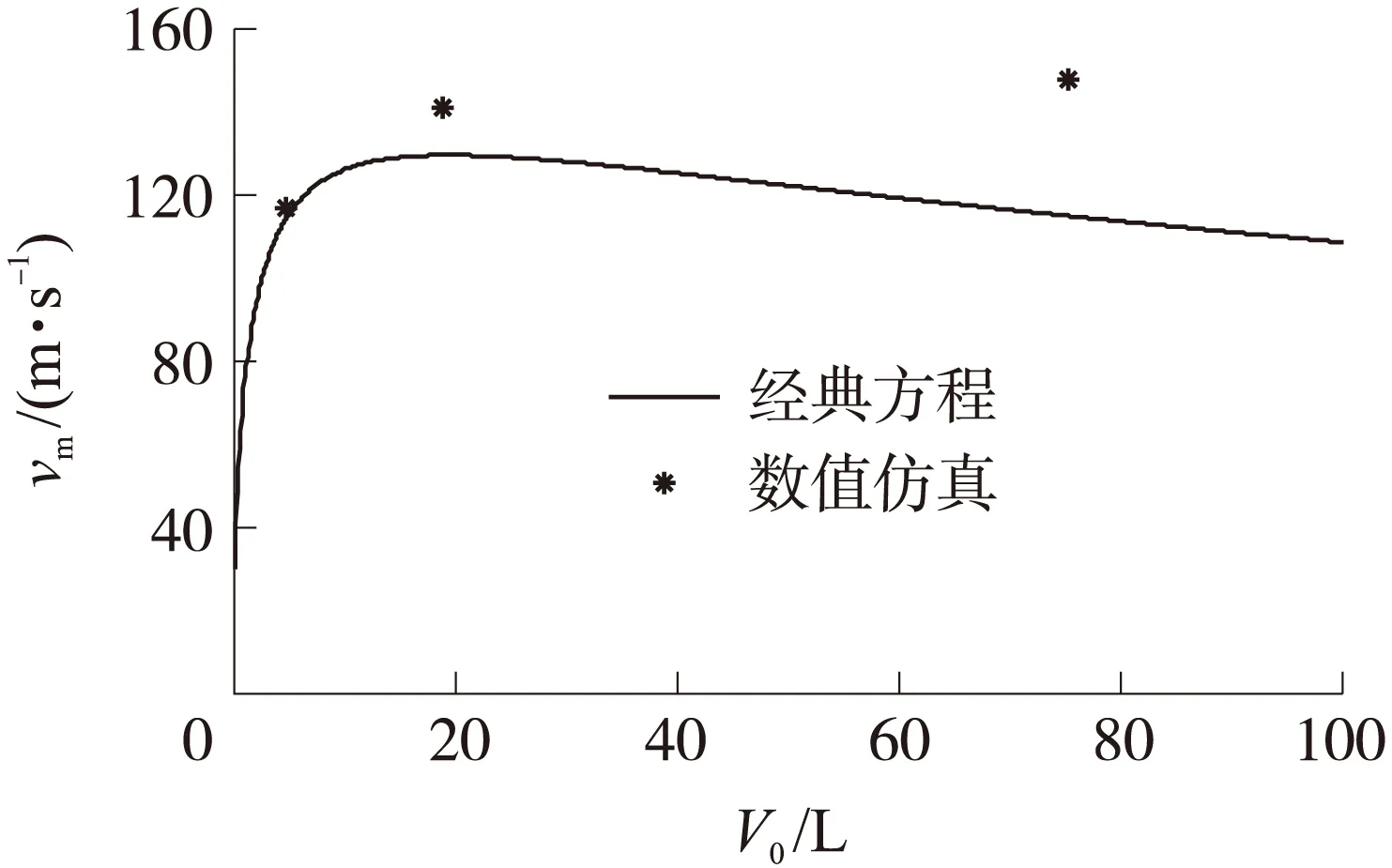
图2　炮口初速随气室容积的变化规律对比

进一步分析理论计算与数值仿真结果不一致的原因,对一级气体炮内弹道经典方程的推导过程进行梳理,发现经典方程中气体密度ρ的表达式为[12]

(2)

式中:m0为气体质量。

式(2)中将气体密度ρ定义为气体质量与炮管容积之比,没有考虑气室容积的大小。当气室容积相对于炮管容积较大时,若忽略气室容积就会导致气体密度显著变大,从而使得气体的附加质量效应人为变大,导致炮口初速变小,甚至出现气室容积越大炮口初速反而越小的情况。故分析认为,当气室容积相对于炮管容积较大时,一级气体炮内弹道经典方程的气体密度表达式中忽略气体容积是不合理的。

2　气体炮内弹道修正方程推导

根据前文的分析,气体密度表达式应考虑气室容积,将气体密度ρ修正为

(3)

基于修正的气体密度表达式,对内弹道方程进行推导,具体过程如下。

根据弹后气体质量守恒方程,并假设任一时刻弹底和膛底之间的气体密度ρ为常量[3],则弹后气体速度vx为

(4)

式中:v为弹丸速度,x为气体微团距炮管左端面的距离。

根据气流动量方程,弹后气体的压力分布为

(5)

式中：pd为弹底压力。则膛内平均压力p为

(6)

根据弹丸运动方程,并引入阻力系数φ1和动态虚拟质量系数φ′,则弹丸的加速度为

(7)

由式(7)有:

(8)

将式(3)和式(5)代入式(6),并与式(8)联立求解,可得虚拟质量系数φ′的表达式:

(9)

气体炮内弹道经典方程[4]中虚拟质量系数φ表达式为

(10)

对比式(9)和式(10)可以看出,修正方程的虚拟质量系数表达式与经典方程明显不同。

根据热力学基本方程,平均膛压为

(11)

将式(9)和式(11)代入式(7)并积分,可以得到:

(12)

式(12)即为一级气体炮内弹道修正方程。

3　气体炮内弹道修正方程验证

为了验证修正方程的正确性和适用性,将修正方程的计算结果与数值仿真结果进行对比。数值仿真在流体仿真软件Fluent平台下进行,采用了与修正方程相同的假设,进行了不同工作气体(空气、氦气、氢气)、不同气室容积下的弹丸膛内运动过程仿真。

具体仿真方法:采用二维轴对称模型,使用结构化网格对计算域进行离散。由于弹丸发射过程中流场计算区域网格随着弹丸的运动会不断变化,数值仿真应用弹簧近似法和动态分层法相结合的域动分层网格更新技术对计算模型进行处理。弹丸受力通过Fluent求解器对弹表面压力积分获得(不考虑弹前压力),加速度根据弹丸受到的气体压力由牛顿第二定律计算获得,弹的速度和位置通过对加速度进行积分求解获得。

编写自定义弹丸运动UDF程序嵌入Fluent求解器控制弹丸运动,采用密度基Couple算法对弹丸发射过程中的流场进行计算,并得到弹丸在膛内任意位置的速度及炮口初速。

主要仿真参数:气室容积分别为4.71 L,18.84 L,75.36 L;气室压力为5 MPa;弹丸质量为2 kg;炮管直径为80 mm;弹丸膛内运动行程为1 m。

当气室容积为18.84 L,工作气体为空气时,弹丸出炮口时的流场压力p分布如图3所示。

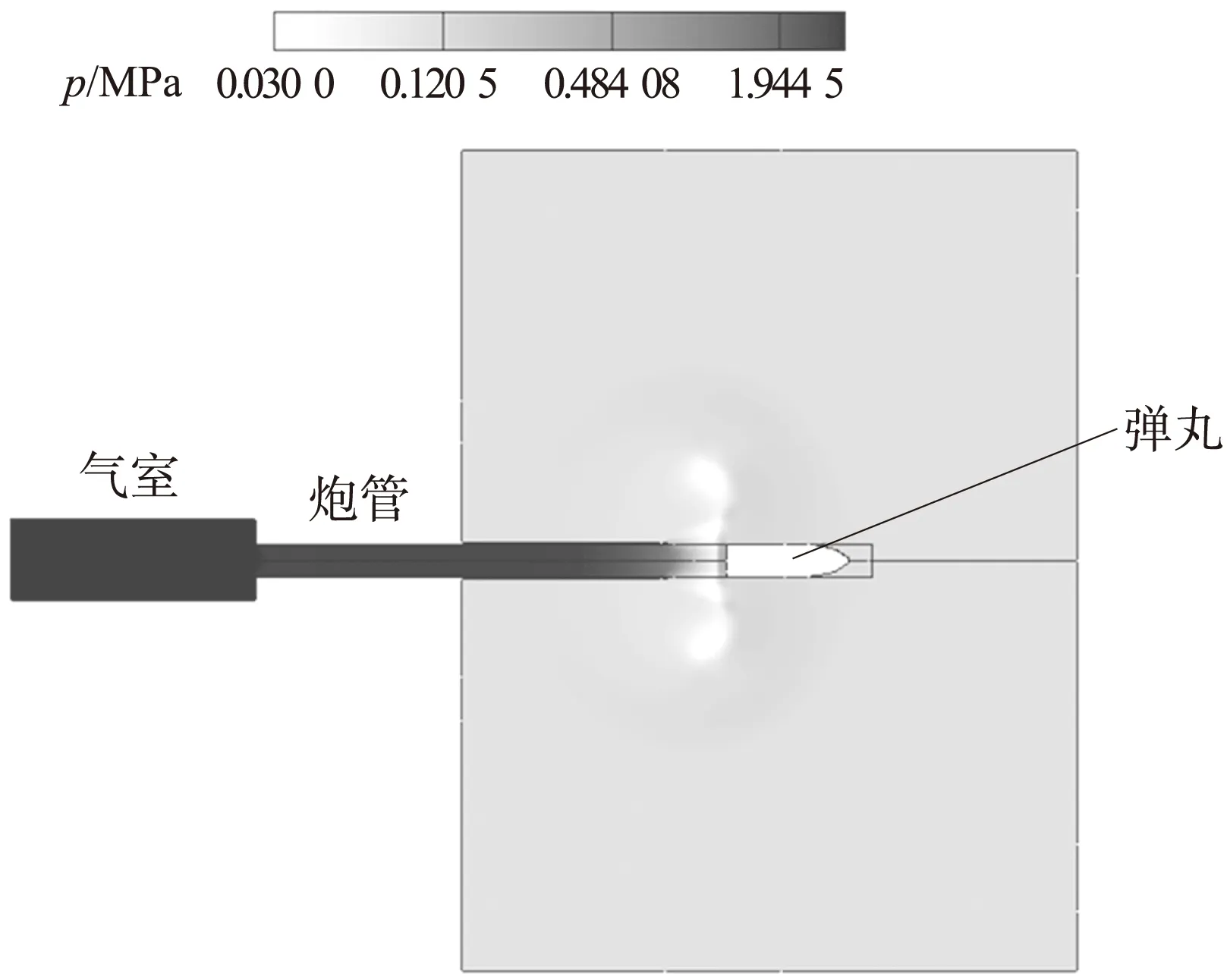
图3　弹丸出炮口时的流场压力分布

不同工作气体、不同容积比r情况下的数值仿真结果与修正方程计算结果、经典方程计算结果的对比如表1和图4所示,其中,e为修正方程与数值仿真结果炮口速度的偏差,容积比r为

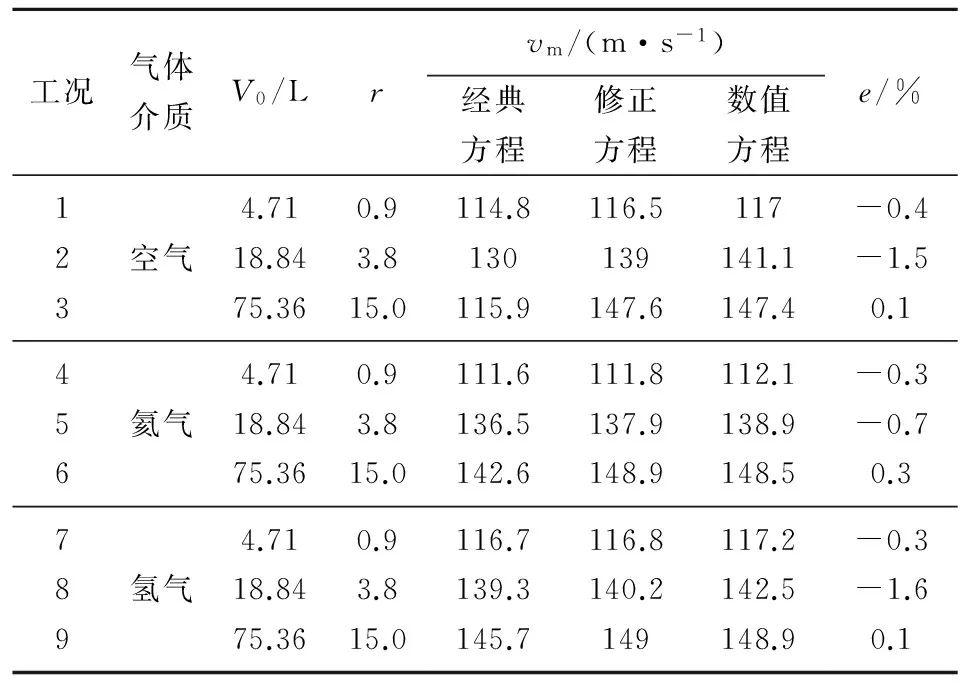
(13)

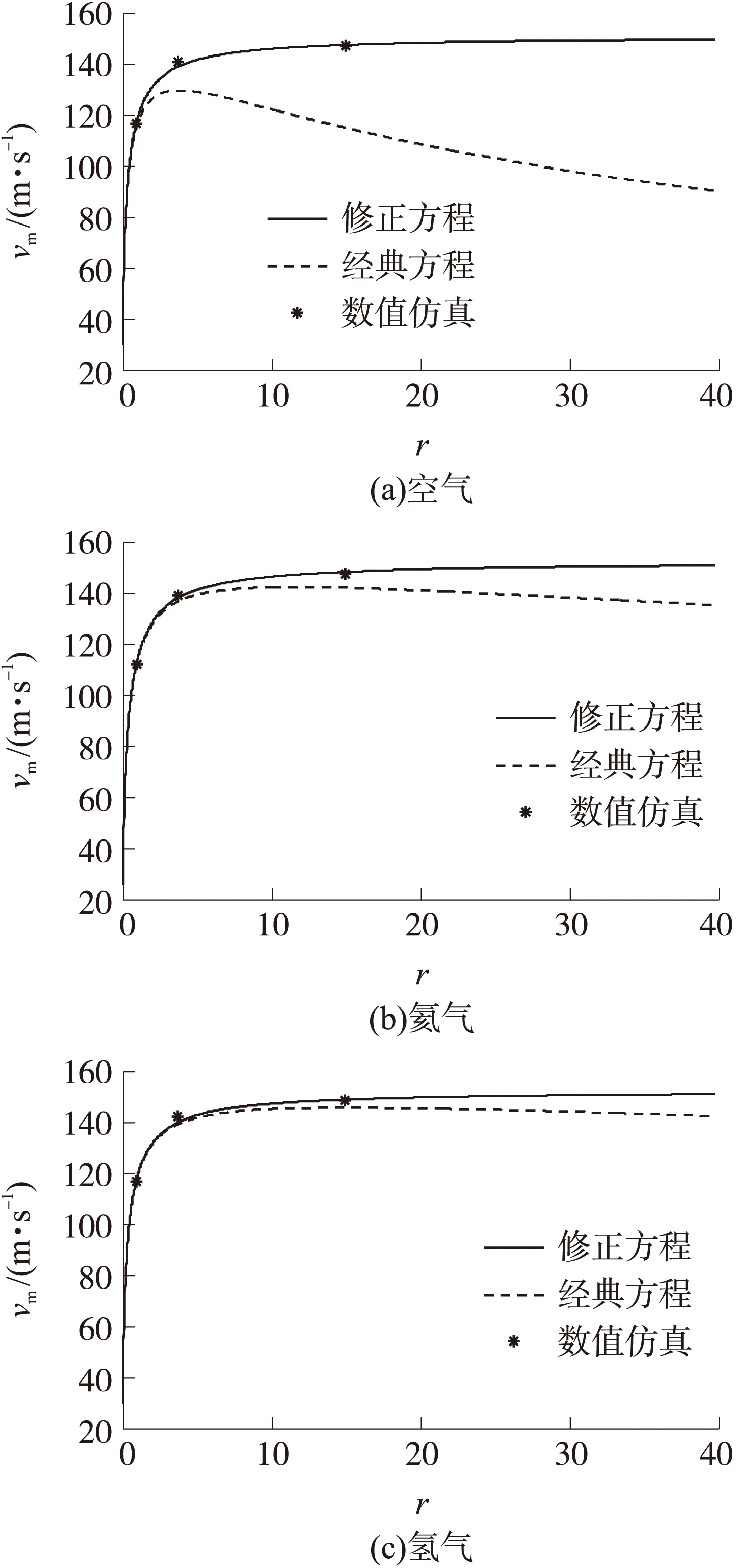
图4　炮口初速随容积比的变化规律对比

工况2下弹丸速度与其在炮膛内的运动行程关系如图5所示。

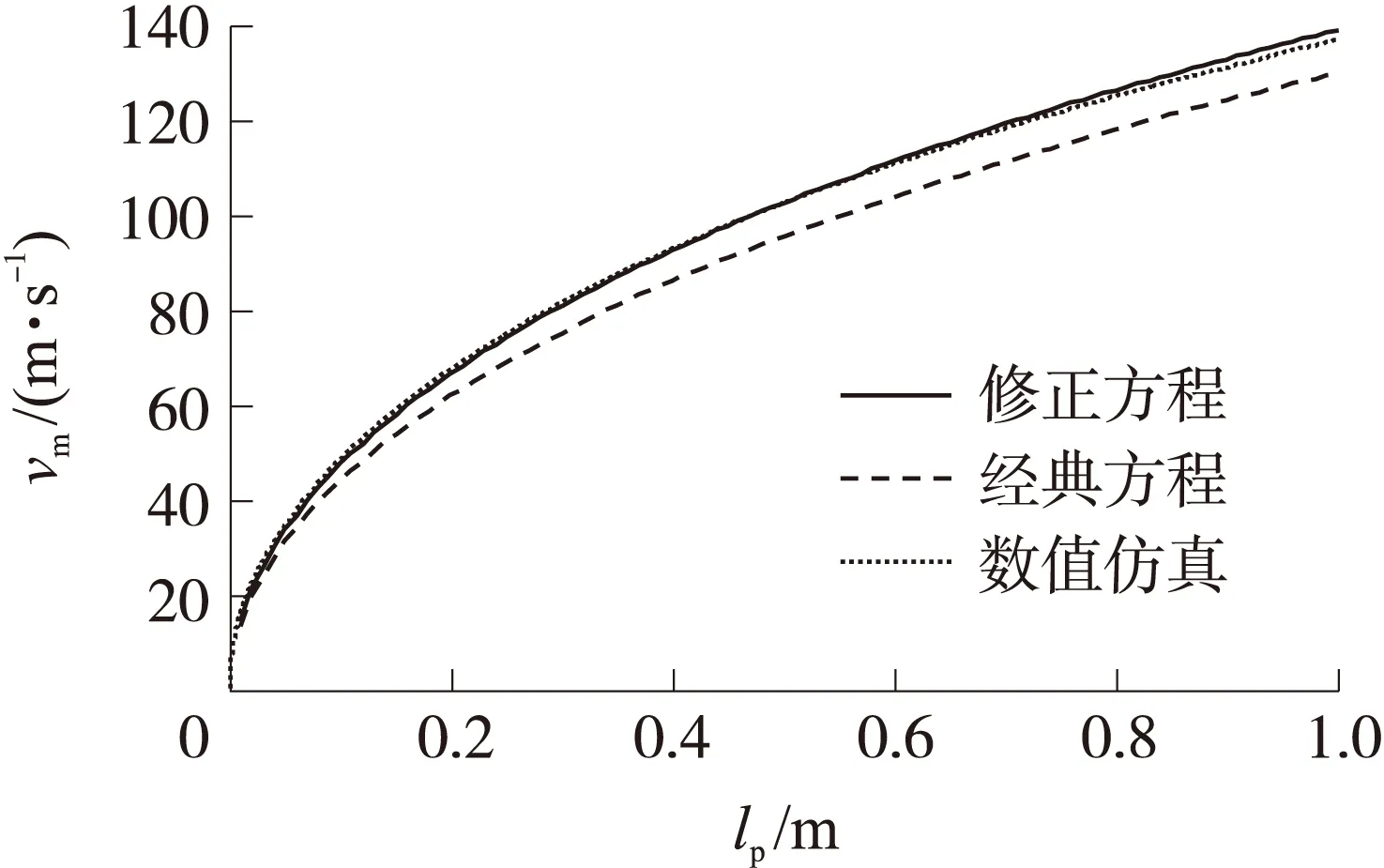
图5　弹丸速度随其行程的变化规律(空气)

从图4、图5可以看出:

①当容积比较小时,经典方程和修正方程的炮口初速曲线基本上是重合的,且与数值仿真结果吻合;但随着容积比的增大,修正方程的炮口初速逐渐增大,与数值仿真结果吻合,而经典方程的炮口初速是先增大后减小。

②气体的摩尔质量越小,经典方程和修正方程的差别越小,这是因为气体摩尔质量小时式(9)和式(10)的差别小,引起的炮口初速偏差也小。

③经典方程、修正方程和数值仿真得到的弹丸在膛内运动速度的变化规律相同,但修正方程与数值仿真结果在数值上更为接近,说明修正方程的计算精度更高。

4　讨论

一级气体炮内弹道经典方程提出较早,且也在实践中得到了应用,从一些公开文献[2]中看,在容积比较小的情况下,经典方程的计算结果与实测结果的偏差并不大,说明经典方程在容积比较小时是适用的,可以满足工程设计精度的要求。但一级气体炮内弹道经典方程的密度表达式忽略了气室容积大小,导致在容积比较大时炮口初速的变化规律不正确,说明经典方程不适用于容积比较大的情况。

由于气体炮的气室容积往往比较大,容积比也较大,若忽略气室容积大小的影响,则可能引入较大的误差甚至错误。因此修正方程基于气室容积不能忽略的考虑,通过修正气体密度表达式,重新推导出炮口初速的表达式。修正方程与经典方程和数值仿真结果的对比表明:在容积比较小时,三者的计算结果基本一致;但在容积比较大时,修正方程的炮口初速变化规律与数值仿真结果一致,而与经典方程明显不同,进一步验证了修正方程的正确性和适用性。

5　结论

本文基于气室容积不能忽略的考虑,对炮管内气体密度表达式进行了修正,联立推导出一级气体炮内弹道修正方程,并将修正方程与经典方程和数值仿真结果进行对比,分析结果表明,经典方程仅适用于容积比较小的情况,而修正方程的适用范围不受容积比大小的限制。修正方程在一定程度上更准确地揭示了炮口初速随气室容积的变化规律,可以用于指导设计,并提高炮口初速在设计阶段的估算精度。根据修正方程进行理论设计,设计可行域较经典方程大,可增加设计的灵活性。

[1]CROZIER W D,HUME W.High-velocity light-gas gun[J].Journal of Applied Physics,1957,28(8):892-894.

[2]BOURNE N K.A 50 mm bore gas gun for dynamic loading of materials and structures[J].Measurement Science and Technology,2003,14:273-278.

[3]SEIGEL A E.The theory of high speed guns，AD475660XAB[R].1965.

[4]王金贵.气体炮原理及技术[M].北京:国防工业出版社,2001.

WANG Jin-gui.Principle and technology of gas gun[M].Beijing:National Defense Industry Press,2001.(in Chinese)

[5]赵俊利,曹锋.气体炮实用内弹道方程及应用[J].火炮发射与控制学报,2003(3):48-51.

ZHAO Jun-li,CAO Feng.Practical interior ballistic equation of the gas gun and its application[J].Journal of Gun Launch and Control,2003(3):48-51.(in Chinese)

[6]DENNY M.Gas gun dynamics[J].European Jouranal of Physics,2013,34:1 327-1 336.

[7]杨均匀,金志明,张小兵.一级轻气炮内弹道数值模拟[J].弹道学报,1998,10(4):21-25.

YANG Jun-yun,JIN Zhi-ming,ZHANG Xiao-bing.Numerical simulation of the interior ballistic process in one-stage light-gas gun[J].Journal of Ballistics,1998,10(4):21-25.(in Chinese)

[8]仲伟君,赵晓利,齐杏林.气体炮内弹道建模与发射环境模拟研究[J].动力学与控制学报,2005,3(1):61-65.

ZHONG Wei-jun,ZHAO Xiao-li,QI Xing-lin.Study on the modeling of the internal ballistic of a gas gun and launching environment simulation[J].Journal of Dynamics and Control,2005,3(1):61-65.(in Chinese)

[9]赵希欣,高元楼.一种气体炮的建模与分析[J].液压气动与密封,2012(10):43-44.

ZHAO Xi-xin,GAO Yuan-lou.Modeling and analysis of a gas gun[J].Hydraulics Pneumatics and Seals,2012(10):43-44.(in Chinese)

[10]胡静,张明安,岳文龙,等.内弹道过程中气体工质做功能力计算分析[J].火炮发射与控制学报,2011(2):82-85.HU Jing,ZHANG Ming-an,YUE Wen-long,et al.Calculation and analysis of gas power capability in process of interior ballistics[J].Journal of Gun Launch and Control,2011(2):82-85.(in Chinese)

[11]夏正友,李建华,褚永胜.基于神经网络的气体炮内弹道仿真与预测[J].现代引信,1998(4):36-40.XIA Zheng-you,LI Jian-hua,CHU Yong-sheng.Imitation and prediction of the gas gun interior ballistics based on neural network[J].Modern Fuze,1998(4):36-40.(in Chinese)

[12]钱林方,侯保林,徐亚栋.火炮弹道学[M].北京:北京理工大学出版社,2009.

QIAN Lin-fang,HOU Bao-lin,XU Ya-dong.Artillery ballistics[M].Beijing:Beijing Institute of Technology Press,2009.(in Chinese)

Modification and Validation of Interior Ballistic Equation for One-stage Gas Gun

LI Feng,BAI Yun-shan,FENG Xiao-wei

(Institute of System Engineering,China Academy of Engineering Physics,Mianyang 621999,China)

In order to improve the accuracy and reliability of the theoretical calculation result,the classical equation for interior ballistics of one-stage gas gun was modified.The problem of classical equation was analyzed.The result shows that the influence of air chamber volume on bullet velocity can not be ignored.A new expression of gas density was presented.According to the equation of mass conservation,the momentum equation of flow,the motion equation of projectile,the adiabatic expansion equation of gas and ideal-gas equation,the modified equation of one-stage gas gun were deduced.The calculation results of muzzle velocity by classical equation and amendatory equation were compared to the result of numerical simulation of interior ballistics.The results show that the muzzle velocity obtained by above mentioned three methods is almost same when the volume ratio of air chamber to gun barrel is very small,but the differences between the results obtained by classical equation and the results obtained by the modified equation and numerical simulation increase markedly with the increase of volume ratio.The classical equation is only suitable for calculating velocity of gas gun with small volume ratio,and the modified equation can be used without volume ratio limit.

gas gun;interior ballistics;muzzle velocity;volume ratio

2014-09-02

中国工程物理研究院高新装备专项

李锋(1980- ),男,工程师,硕士研究生,研究方向为气体炮设计及气体驱动技术。E-mail:15983633005@163.com。

TJ012.1

A

1004-499X(2016)01-0014-05