基于CFD的转管机枪助旋制退器流场超压仿真及对弹丸初速影响分析

王惠源,黄建业,张成卿

(1.中北大学 机电工程学院,太原 030051;2.中国人民解放军96263部队,河南 洛阳 471500)



基于CFD的转管机枪助旋制退器流场超压仿真及对弹丸初速影响分析

王惠源1,黄建业2,张成卿1

(1.中北大学 机电工程学院,太原 030051;2.中国人民解放军96263部队,河南 洛阳 471500)

为了研究转管机枪助旋制退装置流场超压特性及对弹丸速度的影响,运用经典内弹道方程求解流场边界条件,采用计算流体力学中的非粘性、非定常可压缩气体流动方程和动网格技术,对有、无膛口旋转制退装置的膛口流场进行了数值仿真,对弹丸的增速规律进行了计算。对2种情况的仿真结果进行了分析对比,结果表明:有助旋制退装置时膛口流场最大超压值增加约2倍,弹丸速度增加3.61 m/s。

转管机枪;弹丸;超压;内弹道;计算流体力学

膛内的高温高压火药气体在弹丸飞离膛口后形成高度膨胀不足的射流并快速发展成为膛口冲击波,其对武器周围的人员、装备等在安全角度上考虑存在一定的危害,而冲击波的超压峰值是各国军方制定相应安全和防护标准的基本参量之一[1]。本文所使用的助旋制退装置利用后效期火药气体为武器系统提供助旋力矩和制退效率,助旋制退装置的添加改变了后效期火药气体的流场结构,对身管周围的冲击波的超压峰值分布情况同样也将产生一定的影响,并且由于装置侧孔的分流作用,后效期火药气体对弹丸的作用与不含装置时火药气体对弹丸的作用有所不同;而后效期内弹丸的增速规律和增速值影响着武器系统的设计,因此需对添加助旋制退装置对弹丸增速规律和增速值的影响进行讨论和研究。

本文通过膛口流场仿真模拟进行了流场超压及助旋制退装置对弹丸速度影响的研究和讨论。目前对于膛口流场国内外的学者们已经从理论分析和试验方法上进行了大量的研究,如Schmidt等人分别对膛口气流的机理及特征、膛口冲击波的发展变化规律、初始流场以及与膛口流场的作用关系、冲击波超压参数与膛口能量输入率的关系、膛口射流与冲击波的作用关系等问题进行了详细的研究与讨论,并且建立了相应的公式或者经验公式[2-3]。计算机技术的成熟及计算流体力学的发展为膛口流场问题的研究提供了新的途径,如Daniel L C等人分别采用DG及Fluent分析了某口径步枪的膛口流场,并且与实验结果进行对比,结果显示二者吻合得比较好[4]。李鸿志自1977年起分别研究了膛口冲击波的变化规律和减小途径以及膛口流场的形成机理,并且对炮口装置的效率、受力情况进行了分析[5-6]。国内的其他研究者也分别从不同的角度研究了膛口流场、含弹丸的膛口流场、含化学反应的膛口流场,并对膛口冲击波进行了描述,采用动网格和嵌入网格技术对流场进行了模拟[7-9]。

本文针对一种新型的含有助旋制退装置的膛口流场进行数值模拟,分析添加装置后的超压及弹丸增速的影响,其装置的装配体模型如图1所示。

图1　含助旋制退装置的身管组结构图和剖视图

1　计算模型

1.1控制方程

建立二维笛卡尔坐标系下的考虑非粘性的非定常可压缩气体流动方程:

(1)

式中:

U=(ρρuρvE)T

(2)

(3)

(4)

E=p/(γ-1)+ρ(u2+v2)/2

(5)

式中:ρ为密度;t为时间;p为单位面积上的正压力;u,v分别为x,y方向上的速度分量;γ为比热比,在本文中取值为1.33;E为能量。对于理想气体有:

pV=nRT

(6)

式中:R为气体常数，V为气体体积，n为气体的物质的量，T为体系温度。将以上组成封闭方程组,解方程时采用有限体积法进行离散,湍流模型选择单方程的S-A模型。

1.2网格划分和动网格处理

本文建立的模型是以12.7mm口径转管机枪为背景,药室缩进后得出身管长度为1 003mm,忽略膛线作用的影响。身管以及膛口助旋装置为轴对称结构,将其简化为二维模型,可以分析其流场特性,暂不考虑身管组旋转对流场特性的的影响。

整个流场计算域为长度6 000mm,宽度5 000mm,膛底中心位于坐标原点处,枪口方向朝向x轴正方向,其中枪口后方的计算域长度为1 003mm,前方计算域长度为4 997mm,上方和下方的宽度分别距离x轴线为2 500mm和-2 500mm。整个计算域分成膛内区域和膛外区域以方便对膛内进行初始化时的补丁操作。网格划分在膛内以及枪口附近网格密集,远离区域网格较为稀疏。

当考虑耦合弹丸的运动时,需要考虑动网格技术来对流场进行分析,本文的动网格设置使用网格光顺更新法和局部网格重构法来完成。计算开始时定义好网格的初始状态,当弹丸运动后网格产生变形,Fluent在内部自动完成网格变形后的重新划分,对于弹丸的运动本文使用边界型函数进行定义。由于在处理动网格问题上非结构网格有着很好的适应性和灵活性,所以本文对弹和弹周围的区域采用非结构网格划分,对于远离膛口和弹丸的区域采用结构网格划分,这样可提高网格质量和生成速度。不含与含有助旋制退装置的弹丸运动后的网格图如图2(a)和图2(b)所示。

图2　弹丸运动后网格图

1.3初始条件和边界条件

使用Runge-Kutta法求解内弹道方程组,得到内弹道计算结果,如图3、图4所示,图中,vp为弹丸速度。

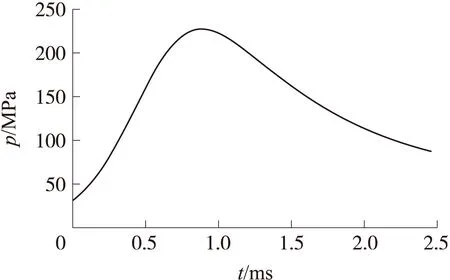
图3　内弹道膛压-时间曲线

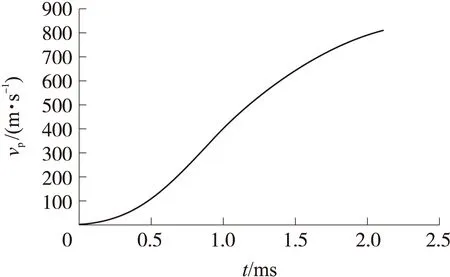
图4　内弹道弹丸速度-时间曲线

当弹丸到达膛口时,膛内气体的压力、速度以及温度分布如下。

膛内压力分布:

(7)

膛内气体速度分布:

(8)

膛内温度分布:

(9)

又

(10)

式中:vg是处于膛口位置时弹底火药气体速度,L是弹后空间长度,vx是分布在x轴上的火药气体速度,mω是装药量,φ1是内弹道次要功系数,m是弹丸质量,pg是膛口处弹底部压力,px是分布在x轴上的火药气体压力,M是火药气体摩尔质量,R是气体常数,ρg是膛内火药气体平均密度,Tx是分布在x轴上的火药气体温度,Vc是药室容积,l是身管行程长度,S是身管横截面面积。

边界条件:膛口处作为压力入口边界条件,计算域远离膛口区域作为压力出口边界条件,膛外区域赋予大气压条件,身管以及助旋制退装置为固壁边界条件,弹丸为运动边界。

2　计算结果及分析

2.1流场分析

图5给出了不含膛口装置的各时刻压力等值线图随时间变化的规律,图中,pm为膛口压力。此时,由于计算时弹丸从膛口处开始运动而非膛内,即没有出现弹丸未完全脱离膛口时的火药气体高速溢出的情况,所以没有冠状激波的产生。从图中的发展过程可以看出,当弹丸出膛口后,膛内火药气体迅速喷出,产生两族膨胀波,随后迅速包围弹丸发展成膛口冲击波。此时由于弹前压力低于弹底压力,弹丸在火药气体的推动作用下不断加速向前运动。从图中可以看出,由于弹丸的存在阻碍了马赫盘的向前发展,随着弹丸不断向前运动,马赫盘从稳定状态过渡到衰减状态,弹丸超过马赫盘后对马赫盘没有影响,同时在弹底部形成弹底激波;当弹丸冲破膛口冲击波后,形成弹丸头部激波,并且这个时刻的弹丸不再受到膛口流场的影响。

图6给出了速度等值线图随时间变化的发展规律,图中vm为膛口冲击波速度。从图中可以看出,弹丸的存在阻碍着马赫盘的发展,这一点与压力等值线图反映出的结果是一致的。在马赫盘内的气流速度高,经过马赫盘气流速度逐渐降低,在弹丸运动过程中同样可以观察到弹底激波的产生。

图7给出了含膛口装置的各时刻压力等值线随时间变化的规律,图中为了显示整体的流场波形,对于膛内和助旋制退装置内部的高压区域未予显示。

从总体上看,膛口装置的不对称性导致了流场的不对称性。当弹丸出膛口后进入助旋制退装置时,此时由于弹丸阻碍了火药气体的轴向膨胀,产生弹底激波,随着弹丸继续向前移动并出膛口装置,弹底激波逐渐减弱并且阵面向上弯曲,如图7(b)所示。随着弹丸继续前移弹底激波逐渐与马赫盘相交,且随着马赫盘的增大和弹底激波的减弱,形成完整的弧面状马赫盘。当弹丸穿过马赫盘后,火药气体流场对弹丸的加速过程结束,进入到由弹前压力主导的减速过程阶段。弹丸在穿过马赫盘到自由飞行阶段之间,还将受到火药气体流场的扰动,产生加速度的震荡。图7(c)所示弹底激波已经完全消失;图7(d)所示弹丸已离开膛口冲击波,此时不受膛口流场作用。可以看到,对于不含助旋制退装置的情况,弹丸运动到4.4ms时冲出膛口冲击波。由此可以看出,由于助旋制退装置的分流作用,装置前出口的气体冲击波将减弱。

图8给出了含膛口装置的速度等值线随时间变化的规律,从图8(b)可以看出,随着弹丸的继续运动,弹底激波减弱,逐渐形成完整的马赫盘。当弹丸穿过马赫盘之后,弹底激波消失,这与不含膛口装置的分析是一致的。从速度等值线图中同样可以反映出由于膛口装置的分流作用,膛口前方的膛口冲击波减弱,弹丸冲出膛口冲击波的时间要比不带膛口装置的时间短。

同时,从含膛口装置的等值线图中可以看出,流场结构的不对称性导致弹丸两侧压力场非对称分布,这将对弹丸的散布产生影响。

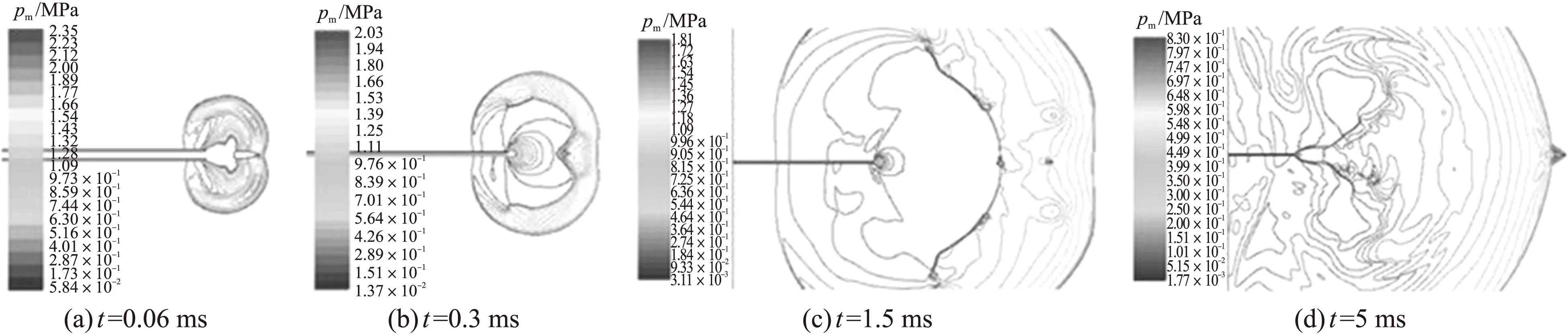
图5　不同时刻不含膛口装置的压力等值线图

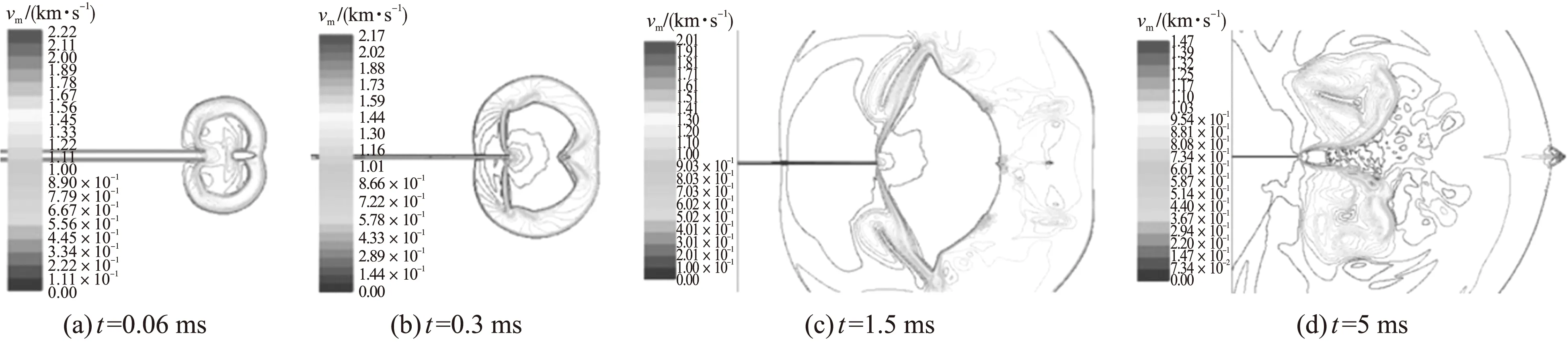
图6　不同时刻不含膛口装置的速度等值线图

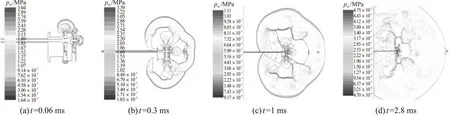
图7　不同时刻含膛口装置的压力等值线图

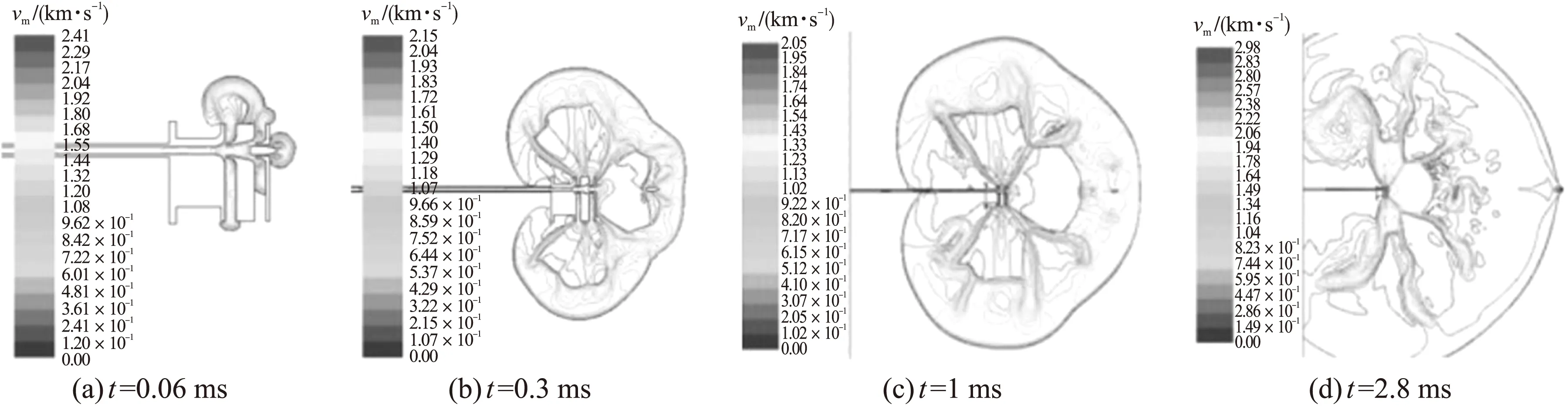
图8　不同时刻含膛口装置的速度等值线图

2.2流场超压值的比较

在膛口附近及身管侧面建立4个监测点监测超压值随时间的变化用以研究流场超压值对人员及周围设备的影响。不含装置和含装置的监测点位置如图9(a)和9(b)所示,图中,a监测点距膛口前端0.5m处,b监测点在膛口处,c监测点和d监测点分别在膛口后方0.35m和0.7m处,4个监测点都位于炮膛轴线1m处。仿真结果如图10和图11所示。

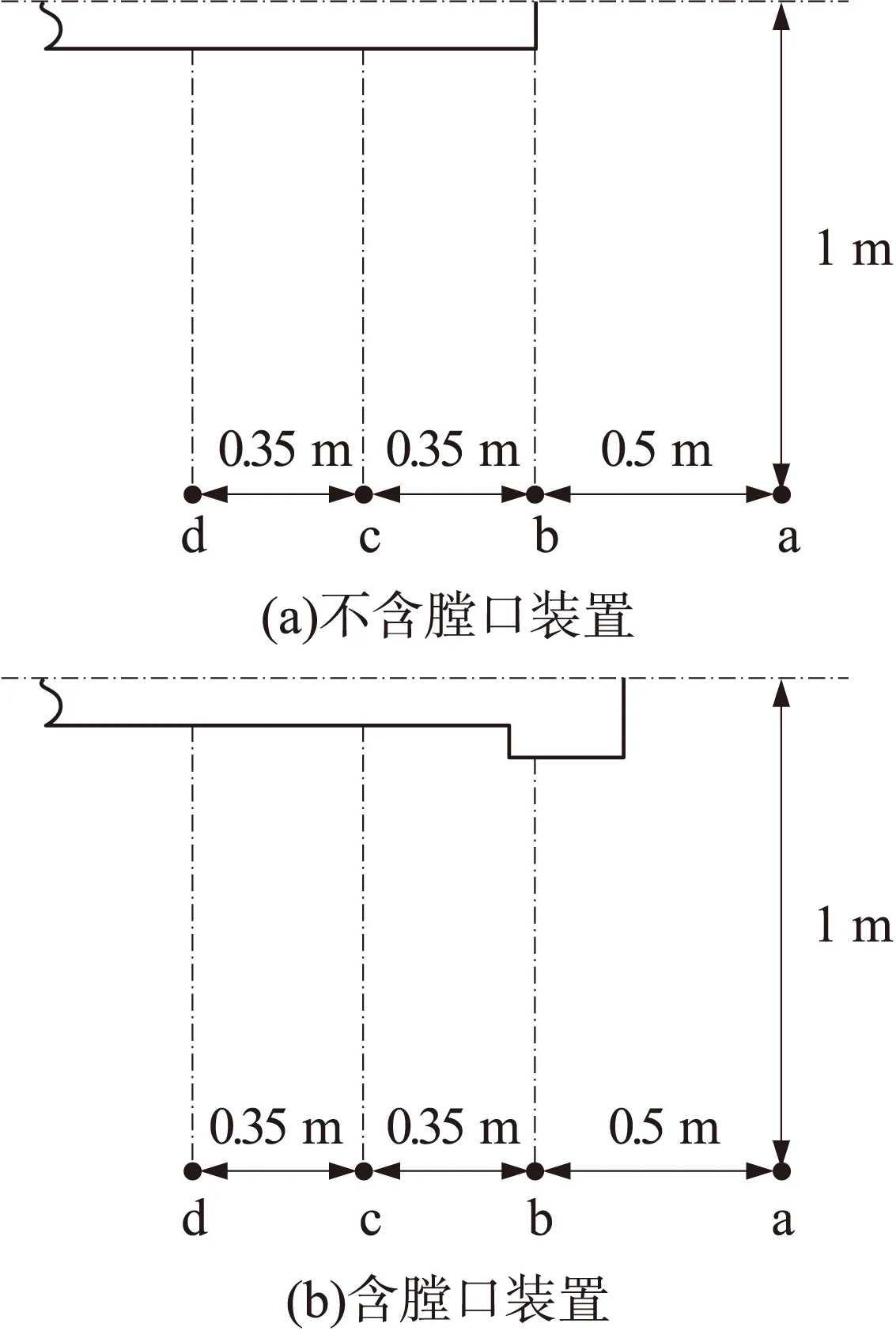
图9　监测点位置示意图

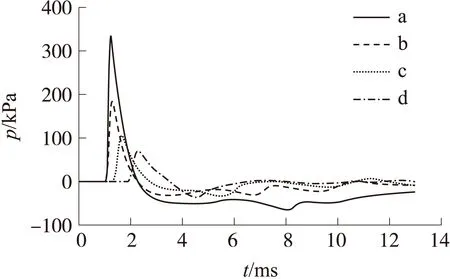
图10　无膛口装置监测点超压值随时间的变化规律

通过数值仿真获得膛口后效期4个监测点超压值随时间的变化规律,如图11所示。从图中可以看出,膛口固定点处超压值变化十分剧烈,具体到达峰值时刻tmax和压力峰值pmax如表1所示。

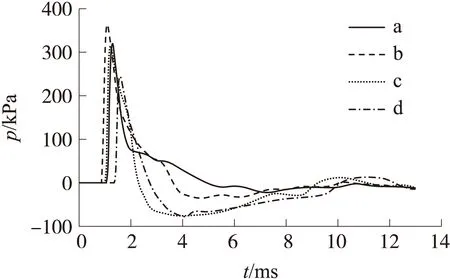
图11　含膛口装置监测点超压值随时间的变化规律

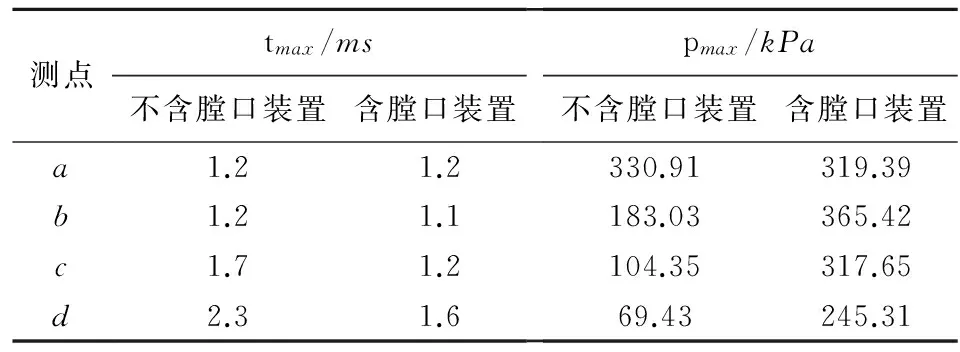
测点tmax/ms不含膛口装置含膛口装置pmax/kPa不含膛口装置含膛口装置a1.21.2330.91319.39b1.21.1183.03365.42c1.71.2104.35317.65d2.31.669.43245.31

从含装置与不含装置的超压比较分析可以看出:对于a点,到达峰值时间和峰值压力变化不大;到达b点峰值时间提前约为0.1ms,峰值压力增大了182.39kPa;到达c点峰值时间提前0.5ms,峰值压力增大了213.3kPa;到达d点峰值时间提前0.7ms,峰值压力增大了112.96kPa。从中可以发现,带膛口装置对膛口的射流产生了非常大的影响,并且添加膛口装置使身管周围的设备以及身管后方的人员所需承受的超压比无膛口装置时要大。

2.3不含与含膛口装置对弹丸增速的影响

根据软件监测出弹底平均压力和弹前平均压力,弹底压力与弹前压力之差为Δp,乘以弹丸横截面积即可获得弹丸在整个流场作用时间内所受轴向合力曲线,通过求导可计算出弹丸的加速度和速度曲线。计算得到的不含膛口装置的压力p,轴向合力F,弹丸加速度ap及弹丸速度vp变化曲线,如图12所示。

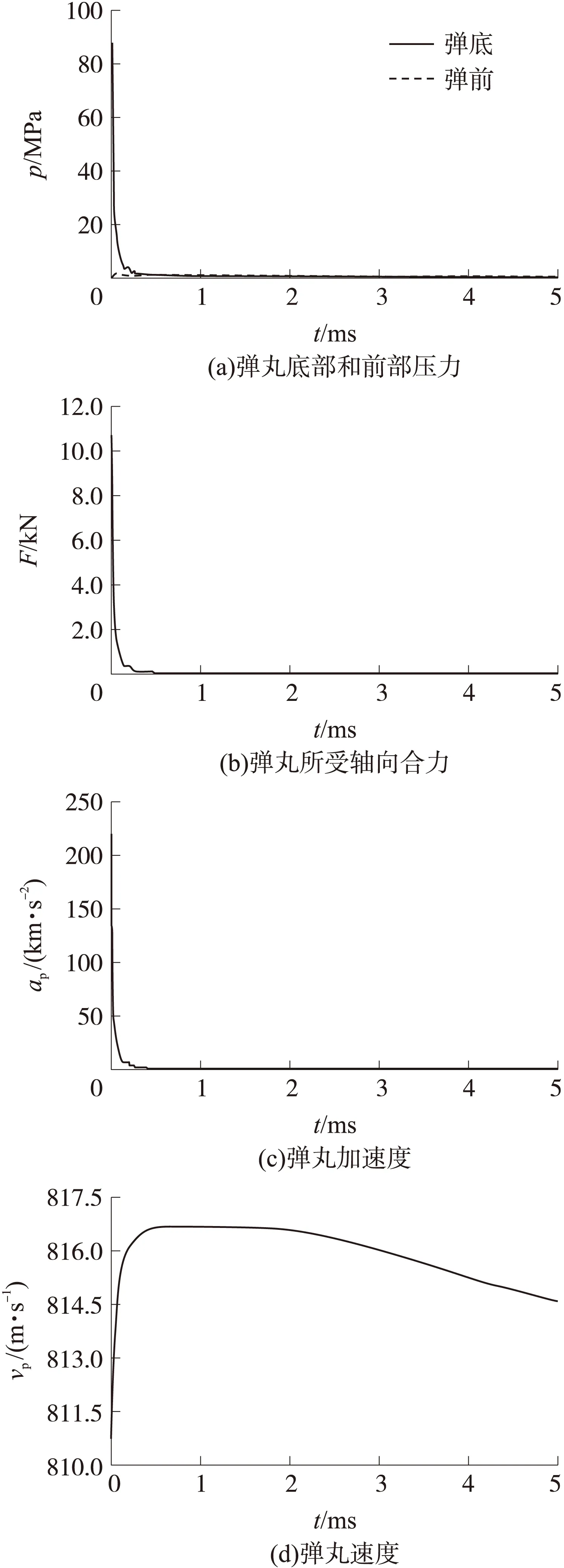
图12　不含膛口装置的计算曲线

从弹丸底部和前部压力随时间的变化曲线可以看出,弹丸刚出膛口时弹底压力远大于弹前压力,并且弹底压力随着弹丸向前方运动而迅速衰减,弹前方压力随着时间的变化不大。从加速度和速度随时间变化曲线图上可以看出,约在0.64ms时弹丸出现最大速度,最大速度值为816.69m/s,此时弹丸穿越马赫盘,弹底激波消失,弹底压力与弹前压力持平,火药气体带弹丸的加速过程结束;随着弹丸的继续运动,弹丸受到马赫盘下游的流场的扰动,此过程对弹丸的加速度产生震荡;此后,随着弹丸的继续运动,弹丸飞离流场作用区域,加速度曲线趋于水平直线,速度曲线近似成直线下降。

计算得到的含膛口装置的各曲线随时间变化如图13所示。

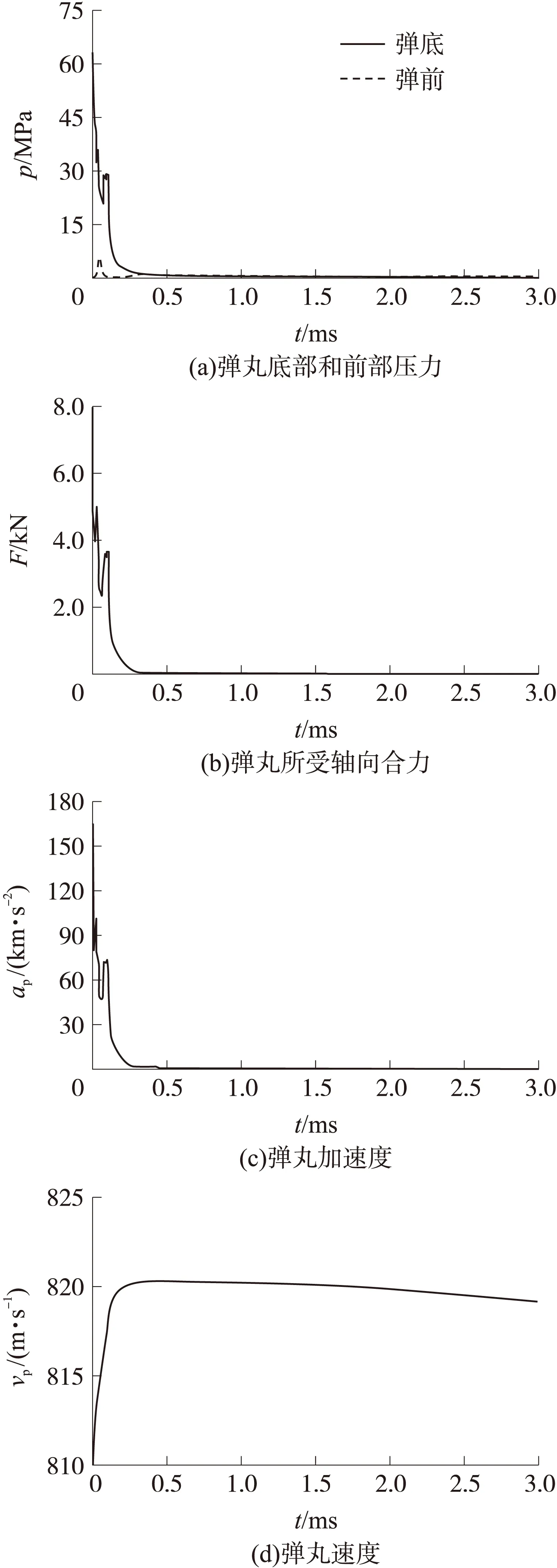
图13　含膛口装置的计算曲线

弹丸在膛口装置内时,虽然膛口装置分流的部分火药气体从侧孔流出,但是火药气体依然给予弹后方很高的压力使得弹丸保持很大的加速度,而分流的作用又使得膛口装置前方的流场减弱。

从弹丸底部和前部压力随时间的变化曲线可以看出,弹丸刚出膛口时弹底压力远大于弹前压力,并且随着弹丸向前方运动在衰减过程中出现2次峰值,这是由于火药气体在装置内部分别进入第1个挡板和第2个挡板入口时产生拥塞现象,导致当地压力突然增大。从加速度和速度等值线图可以看出,加速度的值在助旋制退装置内部同样出现了2次峰值,大约在0.45ms时刻出现最大速度820.3m/s,此时弹丸穿越马赫盘,弹底激波消失,弹底压力与弹前压力持平,随后的弹丸受力规律和不带膛口装置的弹丸受力规律类似。

3　结论

本文针对在膛口处添加助旋制退装置,对不含与含助旋制退装置的膛口流场进行了仿真,得出添加助旋制退装置后膛口附近超压值的变化和对弹丸增速所产生的影响。计算结果表明:添加助旋制退装置后,由于装置侧孔的分流作用对膛口射流结构产生显著的影响,在身管周围与身管后方产生的超压比无膛口装置时要大;同时含助旋制退装置与不含助旋制退装置相比,弹丸出现最大速度时间提前0.19ms,最大速度值增加3.61m/s。

[1]中国人民解放军总参谋部炮兵部.GJB 1158-91,炮口冲击波对人员非听觉器官损伤的安全限值[S].北京:中国人民解放军总参谋部.

Department of Artillery,the General Staff of PLA.GJB 1158-91,Muzzle shock wave on non auditory organ damage safety limit[S].Beijing:The General Staff of PLA.(in Chinese)

[2]SCHMIDT E M,SHEAR D D.Optical measurement of muzzle blast[J].AIAA Journal,1975,13:1 086-1 091.

[3]SCHMIDT E M,GORDNIER R E,FANSLER K S.International of gun exhaust flowfield[J].AIAA Journal,1984,22:1 697-1 710.

[4]DANIEL L C.CFD application to gun muzzle blast-avalidation case sdudy,AIAA-2003-1142[R].2003.

[5]李鸿志,刘晓利.膛口变能量冲击波特性分析:弹道初始参量的影响[J].兵工学报,1993,14(3):17-21.

LI Hong-zhi,LIU Xiao-li.An analysis on the characteristics of variable energy blast wave at the muzzle:the influence of ballistic initial parameters[J].Acta Armamentarii,1993,14(3):17-21.(in Chinese)

[6]李鸿志.炮口装置与效率计算[J].华东工程学院学报,1984(3):1-16.

LI Hong-zhi.Muzzle device and efficiency calculation[J].Journal of East China Institute of Technology,1984(3):1-16.(in Chinese)

[7]马大为.含复杂波系膛口非定常数值研究[D].南京:南京理工大学,1991.

MA Da-wei.Numerical study of the unsteady numerical simulation of the complex wave system[D].Nanjing:Nanjing University of Science and Technology,1991.(in Chinese)

[8]代淑兰,许厚谦,孙磊.含动边界的膛口流场数值模拟[J].弹道学报,2007,19(3):93-96.

DAI Shu-lan,XU Hou-qian,SUN Lei.Numerical simulation of gun muzzle flow field including movable boundary[J].Journal of Ballistics,2007,19(3):93-96.(in Chinese)

[9]姜孝海,李鸿志,范宝春,等.基于ALE方程及嵌入网格法的膛口流场数值模拟[J].兵工学报,2006,27(12):1 512-1 515.JIANG Xiao-hai,LI Hong-zhi,FAN Bao-chun.Numerical simulation of muzzle flow field based on ALE equation and chimera grids[J].Acta Armamentarii,2006,27(12):1 512-1 515.(in Chinese)

Simulation of Flow-field Overpressure of Torque Assist and Brake for Rotating-barrel Machine-gun Based on CFD and Analysis of Its Effect on Projectile Muzzle Velocity

WANG Hui-yuan1,HUANG Jian-ye2,ZHANG Cheng-qing1

(1.College of Mechatronic Engineering,North University of China,Taiyuan 030051,China;2.Unit 96263 of PLA,Luoyang 471500,China)

To study the flow-field overpressure of torque assist and brake of rotating-barrel machine-gun(RBMG)and its effect on projectile velocity,the classical interior ballistic equations were used to solve the flow field boundary conditions,and the unsteady compressible non-viscous gas-flow-equations and dynamic mesh technology of computational fluid dynamics(CFD)were applied,and the flow field of muzzle was numerically simulated.Simulation results of flow fields with and without muzzle torque assist device were discussed,and the projectile velocity was computed.The result shows that the maximum overpressure value of flow field of muzzle with torque assist and brake increases by about 2 times,and the maximum velocity of projectile increases by 3.61 m/s.

rotating-barrel machine-gun;projectile;overpressure;interior ballistics;computational fluid dynamics

2015-06-30

王惠源(1965- ),男,教授,博士,研究方向为高射速发射理论与技术,火炮自动武器仿真技术,枪弹修正控制理论与技术,火炮输弹技术等。E-mail:wanghuiyuannuc@aliyun.com。

TJ012

A

1004-499X(2016)01-0026-07