炮弹地面密集度性能与射程关系仿真

张　浩,闻　泉,王雨时,张志彪,刘锦春

(1南京理工大学 机械工程学院,南京 210094;2黑龙江华安工业(集团)有限公司,黑龙江 齐齐哈尔 161046)



炮弹地面密集度性能与射程关系仿真

张浩1,闻泉1,王雨时1,张志彪1,刘锦春2

(1南京理工大学 机械工程学院,南京 210094;2黑龙江华安工业(集团)有限公司,黑龙江 齐齐哈尔 161046)

为了探讨炮弹三分之二射程地面密集度性能与最大射程地面密集度性能之间的关系,基于蒙特卡罗方法和弹丸空中6自由度弹道方程,采用符合误差因素特征的随机数序列,建立了弹丸地面密集度仿真预测模型,以某155mm口径火炮榴弹为算例,分别得到了对应最大射程和最大射程三分之二处地面密集度仿真数值。结果表明:弹丸最大射程和最大射程三分之二处的地面密集度影响因素差异较大,难以定量对应;用三分之二射程检验弹丸地面密集度指标的方法难以反映最大射程地面密集度性能水平,不宜采用;最大射程地面密集度性能与射角散布几乎无关,而三分之二射程时,射角对地面密集度性能影响较大;弹丸应按最大射程考核地面密集度,火炮系统可按三分之二射程考核地面密集度。

炮弹;密集度;弹道模型;蒙特卡罗方法;仿真

弹丸密集度是指一组弹对其散布中心的分散程度,由许多随机因素引起,主要包括:起始扰动、弹丸外形和质量分布、空气动力参数、气象参数等。弹丸密集度指标是火炮系统的重要性能指标之一[1]。在火炮系统的研制过程中,由于试验场地限制,检验火炮最大射程地面密集度时,火炮最大射程有可能会超出试验场区而无法进行试验,工厂提出使用改变射角的办法改变射程,用最大射程三分之二或五分之四或四分之三处的地面密集度进行生产检验[2]。文献[3]以155mm口径火炮配某型榴弹为例,综合分析地面密集度各种影响因素的概率误差和敏感因子,分别计算出最大射程和三分之二射程地面密集度,并运用统计分析方法,确定了用火炮最大射程三分之二处的地面密集度代替考核最大射程地面密集度性能时的考核指标,但未涉及弹丸地面密集度性能。

蒙特卡罗方法亦称为随机模拟方法,是一种通过随机变量的统计试验、随机模拟来求解数学、物理、工程技术问题近似解的数值方法,其基本思想是利用各种不同分布随机变量的抽样序列模拟给定问题的概率统计模型,给出问题数值解的近似统计估计值[4]。近年来,随着计算机技术的飞速发展,蒙特卡罗方法已被用于进行数学模拟打靶来完成火炮系统一些试验统计量的估计。

本文以某155mm口径火炮榴弹为研究对象,利用Matlab软件建立外弹道弹丸6自由度刚体运动方程,综合考虑影响弹丸地面密集度的各种因素,运用蒙特卡罗方法,分别对弹丸最大射程和最大射程三分之二处的地面密集度进行仿真,分析其地面密集度指标之间的关系。

本文所涉及的均是无控弹药。

1　理论分析

1.16自由度弹道方程

6自由度弹道方程模型精度较高,能完整描述弹丸在空中的各种动态过程,可用于射表编制。本文弹道方程模型选用文献[5]给出的6自由度弹道方程。为简化模型对弹丸及飞行条件作如下假设:

①弹丸是一个外形和质量分布均匀且轴对称的刚体;

②气象条件是标准的,风速恒定;

③忽略科式惯性力的影响。

1.2弹丸密集度指标

对于地面火炮而言,落点处的射程和侧偏是其最重要的弹道诸元，根据概率论中心极限定理,射程和侧偏的概率密度将服从正态分布[5]。在弹道学和射击学中,通常用中间误差E表示射程和侧偏的分布。中间误差E的定义为随机变量出现在均值μ左右各一个E的范围内的概率为50%,如图1所示。由图可见,在均值左右4E(共8E)或3σ(共6σ)范围内随机变量出现的概率大于99%,近似为1。

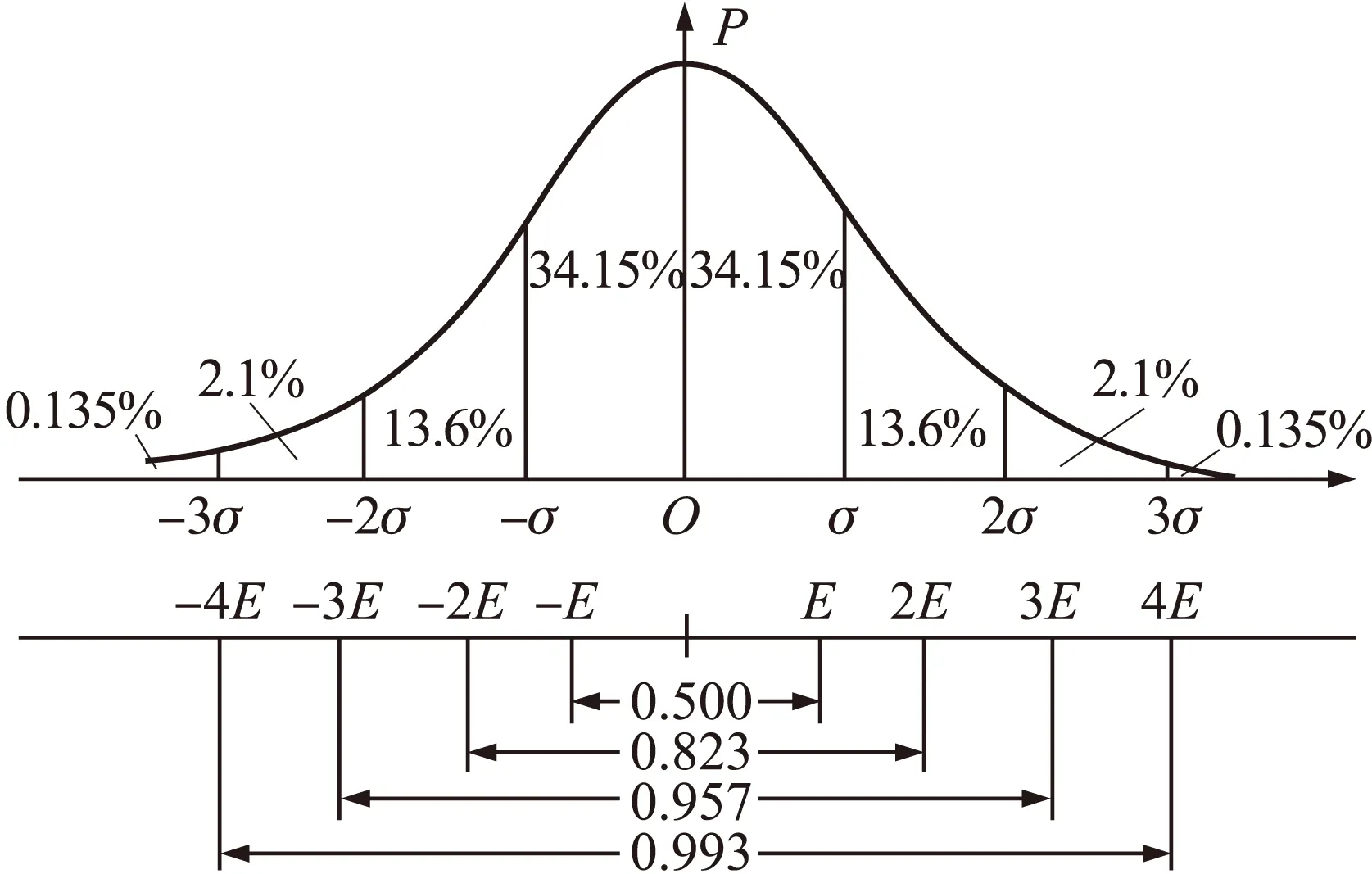
图1　正态分布

n发弹中第i发弹的射程和侧偏分别为xi,zi,则其均值xa,za,均方差σx,σz和中间误差Ex,Ez的计算公式分别为

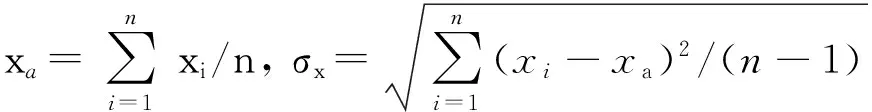
Ex=0.6745σx;

Ez=0.6745σz。

1.3弹丸地面密集度影响因素分析

根据外弹道学理论,由初速v0、射角θ0及弹道系数Cb这3个参量即可得到一条确定的弹丸质心弹道。在弹药发射过程中,各种随机因素使得各发弹之间的v0,θ0及Cb的值存在着微小的随机差异,这是形成弹丸散布的根本原因。例如,弹丸几何尺寸、质量、质量分布的微小变化,每次发射时炮身温度、炮膛干净程度的微小差异,发射药质量、组分、温度和湿度的微小差异,装定射击诸元、瞄准的微小差异,以及气象条件的变化等因素,都是不可避免和随机的,这些微小的随机变化因素所造成的误差可具体地反映在火炮系统的某一性能参数上[6-8]。

①初速散布Ev0。初速散布是由弹质量、发射药药量、药温等随机变化引起的,因此可认为初速是一个正态分布的随机变量。

②射角散布Eθ0。射击时火炮后坐、高低机方向机空回、炮膛轴弯曲等因素共同作用形成射角散布。

③弹道系数散布ECb。弹道系数随机变化是由弹丸质量和阻力系数引起的,后者又是由弹丸姿态变化引起的,包括初始扰动与动力平衡角。

④横向起始偏角Eψ0。

⑤纵风和横风散布Ewx,Ewy。

因此,可用几个综合参数的微小变化(如初速、射角、阻力系数等散布)分析和计算弹丸地面密集度。

2　仿真模型与方法

本文研究弹丸的地面密集度问题,地面密集度计算思路如下:

①基于文献[5]中的6自由度弹道模型,建立外弹道方程;

②结合蒙特卡罗方法,生成符合随机因素分布类型及统计特性的随机数序列来描述随机因素的分布;

③将伪随机数序列代入外弹道方程,计算弹丸落点;

④根据③得到的一系列弹丸落点数据,计算弹丸地面密集度。

基于以上思路,应用Matlab软件建立弹丸地面密集度仿真模型,使用龙格-库塔法求解外弹道方程组。

以某155mm口径火炮榴弹为例进行计算,弹丸初速v0=897m/s,初始射角θ0=50°。计算结果与参考值(榴弹设计计算书中的弹道模型计算结果)对比如表1所示,表中,X表示射程,t表示飞行时间,Y表示最大弹道高,θc表示落角,vc表示落速。

表1　外弹道诸元计算结果与参考值

表1表明,计算结果与参考值基本一致,该外弹道程序符合实际情况,结果具有较高的可信度。

查阅相关资料,影响地面密集度的主要误差因素有[2,5,9]:初速误差、初始射角误差、质量误差、横向起始偏角、纵风和横风。各误差因素均服从正态分布,其中间误差分别确定如下:

①根据装填条件误差[2],装药弧厚误差0.2%,火药力误差0.2%,装药量误差0.01%,弹质量误差0.2%,燃速误差0.2%,挤进阻力误差2%,弹丸定位误差1mm,形状系数误差1%,运动阻力误差2%,计算初速概率误差Ev0=0.959m/s≈1m/s;

②根据GJB3197-1998《炮弹试验方法》中射程与地面密集度试验要求,Em0=(2/3)% m0,m0为标准弹质量;

③对于现代加农炮,文献[9]中取初始射角误差Eθ0=0.2mil,横向起始偏角误差Eψ0=0.2mil;

④根据GJB3197-1998《炮弹试验方法》中射程与地面密集度试验对气象条件的控制,取Ewx=1m/s,Ewz=1m/s。

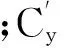
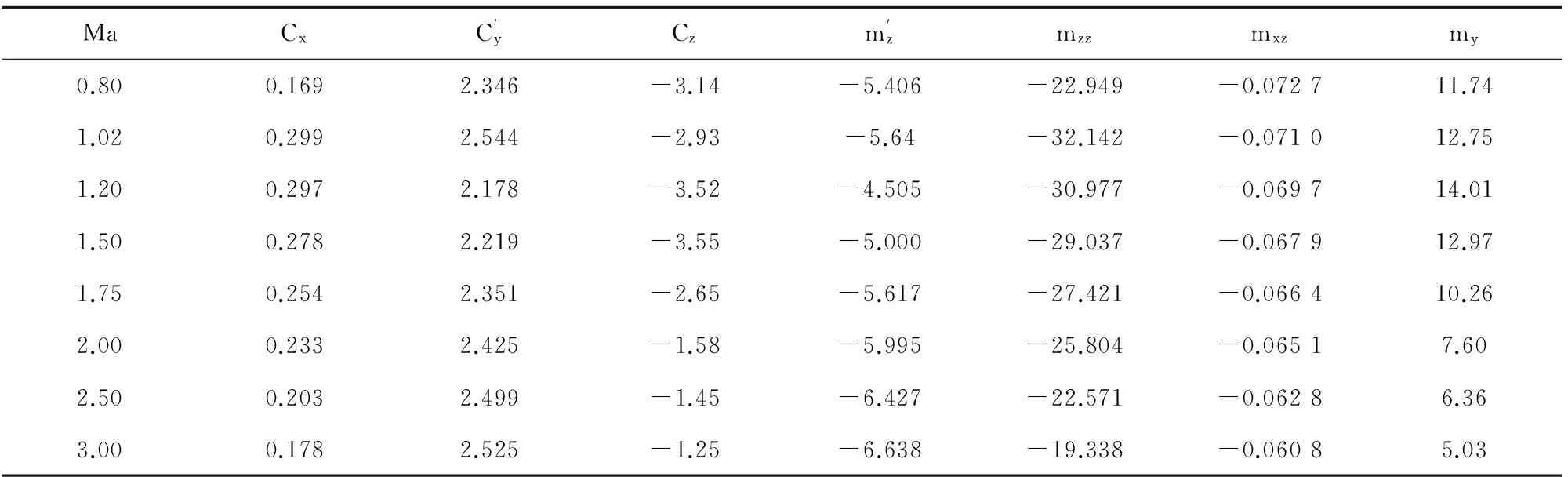
表2　某155 mm榴弹6自由度弹道计算用气动力参数

表3　某155 mm榴弹地面密集度计算值与射表值比较

3　仿真结果及分析

表4　不同射程下EX各因素所占比例

表5　不同射程下EZ各因素所占比例

由表4和表5可看出,最大射程时,射角散布Eθ0对射程地面密集度EX基本无影响,影响射程地面密集度EX的主要因素是质量散布Em0(66.40%)、初速散布Ev0(29.15%)、纵风散布Ewx(4.43%);对于EZ,横风散布Ewz占77.32%,起始偏角Eψ0占22.68%。

综合上述分析,弹丸最大射程和最大射程三分之二处的地面密集度影响因素及其程度均不同。最大射程时地面密集度指标与射角散布无关;而在最大射程三分之二处,无论射角是17°还是72°,地面密集度指标均与射角散布有关。因此,弹丸应取最大射程考核其地面密集度,而火炮系统则不应考核最大射程时的地面密集度,可考核最大射程三分之二或四分之三或五分之四处的地面密集度。

4　结论

通过以上仿真计算,可得到如下结论:

①采用蒙特卡罗方法和6自由度弹道方程建立弹丸地面密集度仿真模型,选用符合影响因素特征的随机数预测弹丸地面密集度,仿真结果与射表值差别较小,具有较高的可信度。

②弹丸最大射程和非最大射程(如最大射程的三分之二或四分之三或五分之四处)地面密集度影响因素及其程度均不同,无明确对应关系,用三分之二射程检验弹丸地面密集度指标的方法难以反映最大射程地面密集度性能水平,不宜采用。

③最大射程地面密集度性能几乎与射角无关,而三分之二射程时,射角对地面密集度性能影响较大。

④弹丸应考核最大射程地面密集度,火炮系统可按三分之二或四分之三或五分之四射程考核地面密集度。

[1]浦发.外弹道学[M].北京:国防工业出版社,1980:289-291.

PUFa.Externalballistics[M].Beijing:NationalDefenceIndustryPress,1980:289-291.(inChinese)

[2]郭锡福.远程火炮武器系统射击精度分析[M].北京:国防工业出版社,2004:42-48.

GUOXi-fu.Firingaccuracyanalysisforlongrangegunweaponsystems[M].Beijing:NationalDefenceIndustryPress,2004:42-48.(inChinese)

[3]郭锡福.火炮武器系统外弹道试验数据处理与分析[M].北京:国防工业出版社,2013:100-105.

GUOXi-fu.Exteriorballistictestdataprocessingandanalysisforgunweaponsystems[M].Beijing:NationalDefenceIndustryPress,2013:100-105.(inChinese)

[4]徐钟济.蒙特卡罗方法[M].上海:上海科学技术出版社,1985:5-7.

XUZhong-ji.MonteCarlomethod[M].Shanghai:ShanghaiScienceandTechnologyPress,1985:5-7.

[5]韩子鹏.弹箭外弹道学[M].北京:北京理工大学出版社,2014:118-159.

HANZi-peng.Externalballisticsofprojectileandrocket[M].Beijing:BeijingInstituteofTechnologyPress,2014:118-159.(inChinese)

[6]王宝元.中大口径火炮射击密集度研究综述[J].火炮发射与控制学报,2015(2):82-86.

WANGBao-yuan.Reviewofresearchonfiringdispersionofmediumandlargecaliberartillery[J].JournalofGunLaunch&Control,2015(2):82-86.(inChinese)

[7]鲁玉祥,崔万善,徐坚,等.火炮最大射程地面密集度分析与预测[J].火炮发射与控制学报,2011(2):39-42.

LUYu-xiang,CUIWan-shan,XUJian,etal.Analysisandpredictionofgunmaximumrangegrounddispersion[J].JournalofGunLaunch&Control,2011(2):39-42.(inChinese)

[8]钱明伟,王良明,郭锡福.火炮武器高原射击时的弹道特性研究[J].弹道学报,2009,21(4):21-25.

QIANMing-wei,WANGLiang-ming,GUOXi-fu.Ballisticanalysisforartillerysystemsfiringonplateau[J].JournalofBallistics,2009,21(4):21-25.(inChinese)

[9]王兆胜.火炮射击精度分析的模型与应用[M].北京:国防工业出版社,2013:116-119.

WANGZhao-sheng.Analysismodelofgunfiringaccuracyandtheirapplications[J].Beijing:NationalDefenceIndustryPress,2013:116-119.(inChinese)

SimulationResearchofRelationshipBetweenGroundDispersionPerformanceofProjectilesandFiringRange

ZHANGHao1,WENQuan1,WANGYu-shi1,ZHANGZhi-biao1,LIUJin-chun2

(1.SchoolofMechanicalEngineering,NanjingUniversityofScienceandTechnology,Nanjing210094,China;2.HeilongjiangHuaanIndustrial(Group)Ltd,Qiqihaer161046,China)

Inordertostudytherelationshipofartilleryprojectilesground-dispersionperformancebetweentwo-thirdsfiring-rangeandmaximumfiring-range,theMonte-Carlomethodand6-DOFtrajectoryequationwereapplied,andthesimulationpredictionmodelofground-dispersionofprojectileswasestablishedbyapplyingrandomnumberseriesaccordingtothefeatureoferrorfactor.Thecorrespondingground-dispersionsimulation-valuesunderthetwo-thirdsfiring-rangeandmaximumfiring-rangewereobtainedtakinga155mmcaliberartilleryprojectileforanumericalexample.Theinfluencefactorsofprojectiledispersionofmaximumfiring-rangeandtwo-thirdsfiring-rangearequitedifferent,anditisdifficulttoquantificationallycorrespond.Themethodofgrounddispersionindexoftwo-thirdsfiring-rangecan’treflecttheperformancelevelofmaximumfiring-rangedispersion,whichcan’tbeapplied.Themaximumfiring-rangedispersionperformanceisirrelevantwithfire-angle,butthefireanglehasagreatimpactonthedispersionperformanceundertwo-thirdsfiring-range.Artilleryprojectilesground-dispersionperformanceshouldbeevaluatedbythemaximumfiringrange,andthedispersionperformanceofartillerysystemscanbeevaluatedbythetwo-thirdsfiring-range.

artilleryshell;dispersion;ballisticmodel;Monte-Carlomethod;simulation

2015-09-25

张浩(1992- ),男,硕士研究生,研究方向为引信、弹药技术。E-mail:752283615@qq.com。

王雨时(1962- ),男,教授,研究方向为引信技术。E-mail:wyshi204@163.com。

TJ013.2

A

1004-499X(2016)01-0056-04