MIMO系统中一种正交相移键控均衡技术

关 浩，朱耀麟

（西安工程大学电子信息学院，西安 710048）

MIMO系统中一种正交相移键控均衡技术

关 浩，朱耀麟

（西安工程大学电子信息学院，西安 710048）

针对MIMO（多输入多输出）系统传输信道模糊、信道容量受限以及信号误码率较高的问题，提出先对信号进行QPSK（正交相移键控）调制，然后再将改进的CMA（恒模算法）与自适应波束形成技术结合用于MIMO系统中对信号进行均衡处理，使信号具有较强的抗干扰性，同时增强传输信息的可靠性和稳定性。实验结果表明，采用QPSK调制均衡技术可以解决信道容量与误码率相矛盾的问题，降低码间串扰和信道干扰，还可以校正相位误差，获得较快的收敛速度以及低误码率，使信号得到最佳恢复。

多输入多输出系统；正交相移键控调制；恒模算法；自适应波束形成

0 引 言

在无线通信领域，MIMO（多输入多输出）系统凭借容量大和频谱利用率高的特点［1］，受到广泛关注。然而，在高速传输系统中，多径效应与频率选择性衰落等因素对符号间干扰的影响较为严重［2］，近年来，有许多专家学者从信道编码方式、均衡技术等方面对MIMO系统进行了深入的研究与系统设计。清华大学的孙守宇等人提出了一种修正的CMA（恒模算法），可以使被修正的误差函数最小化，收敛速度加快，输出的符号间干扰小［3］；Shi Kun等提出了基于MIMO的改进CMA和SE-CMA（符号误差函数CMA）［4］。由于MIMO信道是一个时变、非平稳的系统，所以减少ISI（码间串扰）的影响、提高频谱利用率成为研究的重点，将改进CMA与自适应波束形成技术结合应用于MIMO系统中，可以自动跟踪并调整信道参数，使传输的信息更加准确。

1 系统模型

在频谱资源相对贫乏的通信中，MIMO系统可以很好地提高系统的抗衰落和抗噪声性能，其容量是单天线的近40倍，可以实现数据的快速传输，提高传输的质量［5］。图1所示为MIMO系统模型。

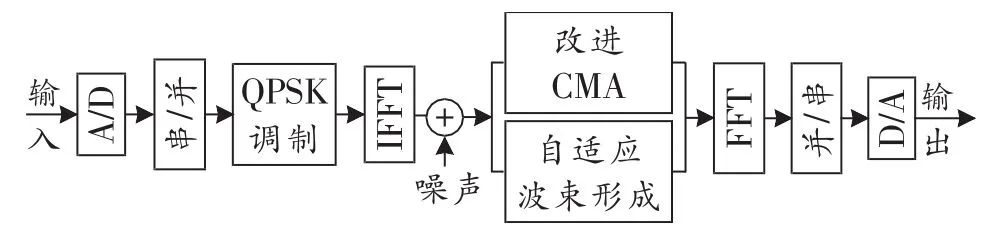
图1 MIMO系统模型

其中，在CMA后采用了自适应波束形成技术，充分利用信号的恒模特性优化其代价函数，最大程度地恢复恒模信号。本文采用信道系数干扰比对

MIMO系统性能进行评价，其定义如下［6］：

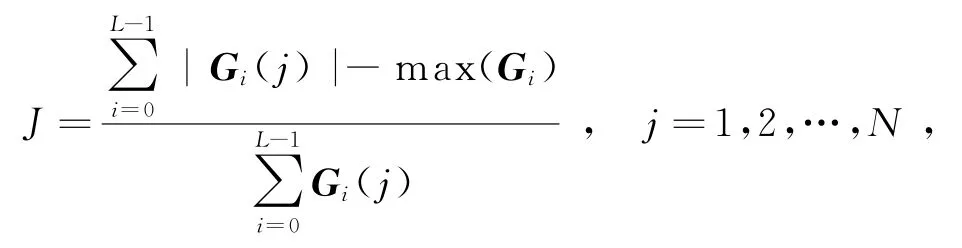
式中，L为整体信道的长度；N为等效信道的数量；Gi为均衡后信道矩阵。

在MIMO系统中，信道的容量为

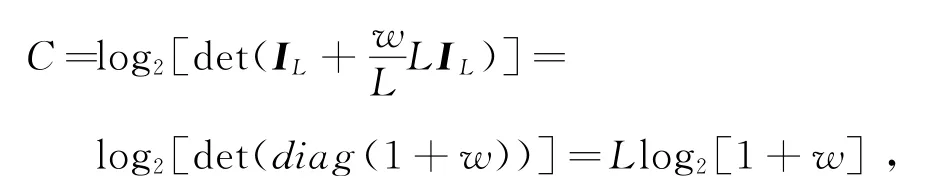
式中，det［］表示矩阵的行列式；IL为L×L的单位矩阵；diag（1+ω）表示将信噪比矩阵对角化；ω为每个信道的信噪比。从公式中可以看出，MIMO系统的信道容量是单天线容量的L倍，若天线数不断增加，则信道容量也不断增大，这样可以在接收端天线合并时减少衰落的影响，增加信噪比［7］。

2 改进CMA及自适应波束形成技术

之后，信号经过自适应波束形成，可以依据环境噪声场的不同自动调整参数，利用恒模阵波束形成器最大程度地恢复恒模信号［9］，并根据最小均方误差准则估计误差的平方值最小化，抑制干扰并检测出有用信号。

3 仿真结果及分析

图2所示为4×4 MIMO均衡系统在瑞利信道中的BER（误码率）曲线。由图可见，采用MMSE（最小均方误差）准则均衡后的BER近似值远小于ZF（迫零）准则下的理论值，也低于MRC（最大比合并）理论值，其BER最小。

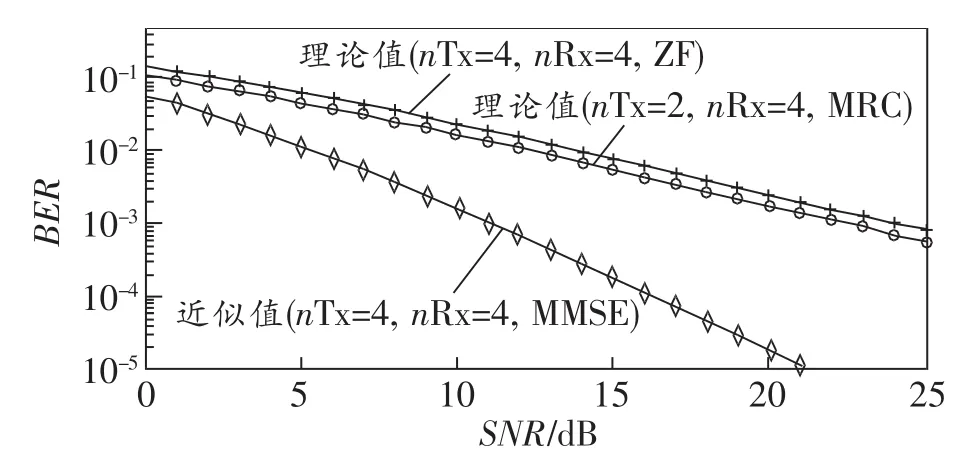
图2 QPSK调制均衡系统的BER曲线

图3给出了在相同SNR（信噪比）下采用改进CMA和原始CMA时的BER曲线。可以看出，采用改进CMA比原始CMA获得了更低的BER。

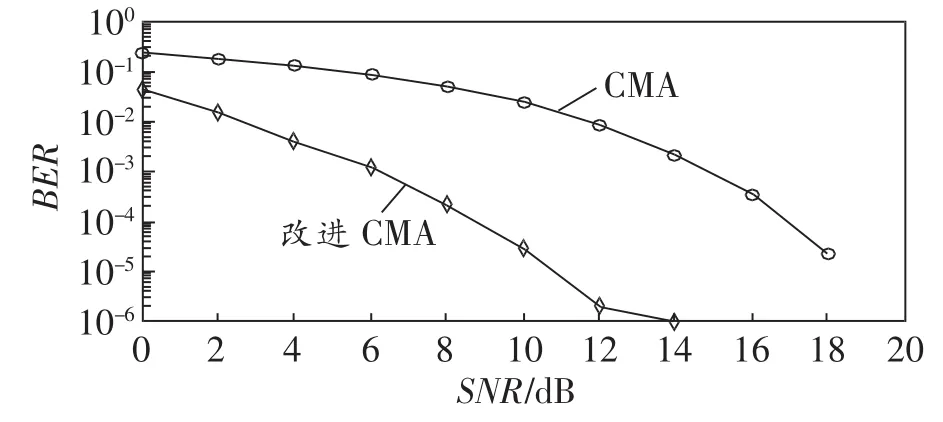
图3 相同SNR下的BER曲线

图4所示为SNR与信道容量的比较。由图可见，在相同SNR下，MIMO系统的容量是单线传输的3倍多，表明信息传输量大。

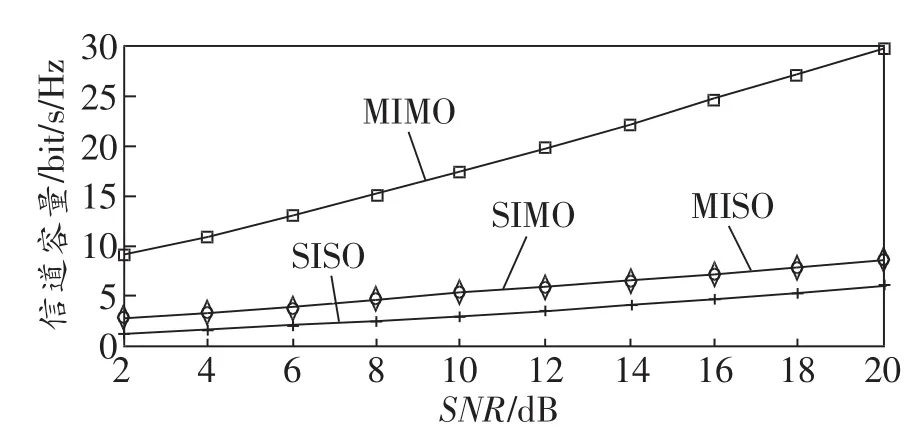
图4 SNR与信道容量比较曲线

图5所示为均衡后系统传输信号的星座图及均衡误差。均衡系统的滤波器阶数为11，星座点数为2 000，SNR为25 dB，步长因子为0.001。在图5的基础上，对传输系统进行16相位均衡，星座点数为5 000，并给出了ISI曲线，如图6所示。从图中可以看出，采用此均衡技术可以明显提高星座点的收敛速度，降低BER及ISI的影响。

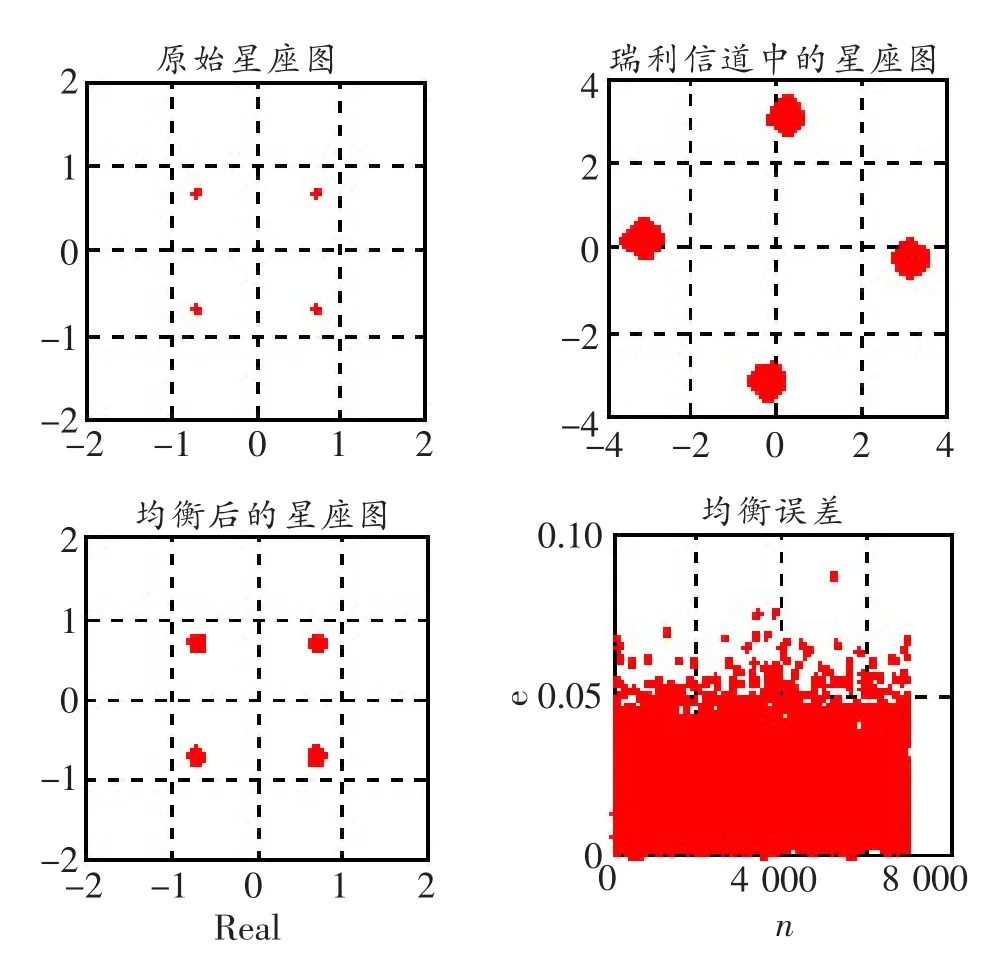
图5 4相位均衡算法星座图及均衡误差

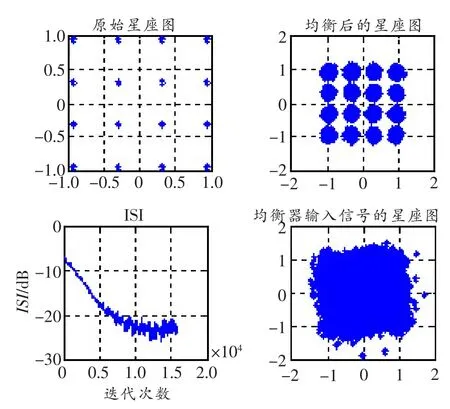
图6 16相位均衡算法星座图及ISI

4 结束语

在MIMO系统中采用QPSK调制、盲均衡算法以及自适应盲均衡波束形成技术，大大提高了信道容量，而且可以在接收端有效地克服ISI，恢复出多天线传输的信息。同时，采用改进CMA可以使星座点收敛速度变快，均衡误差减小，加之利用自适应波束形成技术，减少了信道干扰，有利于信号在信道中传输，提高了信号传输的准确性。MIMO系统中的均衡技术在实际应用中具有十分重要的意义，尤其在提高接收信号质量和信息准确性以及可靠性方面，具有较高的研究价值。

［1］ 史岩岩.MIMO信道盲均衡算法研究［D］.南京：南京信息工程大学，2014：54-65.

［2］ 陈旭.基于MIMO系统的盲均衡算法研究［J］.电子科技，2014，27（09）：13-15.

［3］ 孙守宇，郑君里，张琪.盲信道均衡中的一种修正恒模法［J］.清华大学学报：自然科学版，2003，43（7）：923-926.

［4］ Shi Kun，Zhang Xudong.Blind equalization of MIMO systems based on orthogonal constant modulus algorithm［J］.Journal of Electronics（China），2006，23 （2）：181-183.

［5］ 杨雄，姜玉洁，刘泽，等.基于MIMO-OFDM的卫星通信中的MMSE-PIC算法［J］.广东通信技术，2015，35 （01）：51-55.

［6］ 黄韬，袁超伟，杨睿哲，等.MIMO相关技术与应用［M］.北京：机械工业出版社，2006：97-102.

［7］ 杨尚贤，王明皓.MIMO系统的波束形成技术研究及其仿真［J］.电子设计工程，2012，24（20）：93-95.

［8］ 杨琨，王华奎.恒模算法的一种在线自适应初始方法［J］.太原理工大学学报，2005，36（3）：225-227.

［9］ 彭青，李银伟，郭志军.认知MIMO系统中波束形成和功率的联合控制博弈算法［J］.电信科学，2015，31 （08）：

39-45.

An Equalization Technology of QPSK Modulation in MIMO System

GUAN Hao，ZHU Yao-lin
（College of Electronics and Information，Xi’an Polytechnic University，Xi’an 710048，China）

To solve the problems of the channel blur，limited channel capacity and higher error rate in Multiple-Input Multiple-Output（MIMO）system，we propose a new channel equalization method to compensate the channel distortion to increase the anti-interference，and enhance the reliability and stability of the transmission system.The method is based on the combination of Constant Modulus Algorithm（CMA）and adaptive beamforming technology in MIMO system with Quadrature Phase Shift Keying（QPSK）modulation.The experimental results show that the proposed QPSK equalization technique can solve the contradictory problem between channel capacity and the bit error rate，and reduce the inter-symbol interference and channel interference.In addition，it can achieve the best performances by correcting the phase error with faster the convergence speed and lower bit error rate lower.

MIMO system；QPSK modulation；CMA；adaptive beamforming

TN929.5

A

1005-8788（2016）03-0073-03

10.13756/j.gtxyj.2016.03.023

2015-12-16

陕西省教育厅自然专项项目（14JK1318）

关浩（1989-），男，山西临汾人。硕士研究生，主要从事无线通信技术的研究。