基于真实吐露贪婪机制的多Agent单机调度问题

姜　雪，全雄文，陈秋双

(南开大学计算机与控制工程学院，天津300071)



基于真实吐露贪婪机制的多Agent单机调度问题

姜雪，全雄文，陈秋双

(南开大学计算机与控制工程学院，天津300071)

在分布式环境下，从组合拍卖的角度出发研究了多Agent的单机调度问题，设计了一种贪婪机制.该贪婪机制包括贪婪分配算法和贪婪支付算法两部分，首先贪婪分配算法以资源Agent收益最大为目标解决组合拍卖中的竞胜标问题，然后贪婪支付算法以第二价格支付的形式确定中标者应该支付的最小费用.本文证明了该贪婪机制的真实吐露性，并通过算例说明设计机制的可行性与有效性.最后进行仿真实验比较该贪婪机制与线性规划方法的求解效果，结果表明，对大规模问题，该机制能够快速得到使系统总收益近似最优的调度方案.

多Agent单机调度；组合拍卖；真实吐露；贪婪机制

1　引　言

21世纪，在制造业全球化的大背景下，多企业的协同设计制造现象越来越普遍.国际分工和企业间分工日益深化和细化，对于非核心业务，企业通常以原始设备制造商(original equipment manufacturer，OEM)等方式外包给其他企业.典型的如小米公司，其2013年产值突破了300亿元.小米手机的设计由其设计部通过互联网联合小米发烧友共同完成，生产由多个OEM协同实现，这种模式被业界称“小米模式”.当前这种基于互联网的协同设计和生产模式[13]受到了广泛关注，已成为实现我国制造业结构转型的一个重要途径.为了实现“分散资源集中使用，集中资源分散服务”的目标，必须建立面向服务的制造资源公共服务平台.但是，现有的制造资源服务平台提供的预定与收费规则都很简单，缺乏互相之间的协调机制和对资源的优化配置功能.这就需要设计更加高效合理的运营模式，在满足客户Agent对制造资源服务需求的同时，保证资源Agent的收益，这样才能吸引和鼓励更多的资源Agent参与和提供制造服务，实现制造资源的整合和优化配置.

在处理分布式环境下的多Agent调度问题时，由于Agent可能不愿意或无法与其他Agent或统一协调者交换所有的私有信息，因此如何恰当地表示公有信息与各Agent私有信息，设计有效的协调通讯协议，在合理的计算时间内得到合理的分配方案就成为多Agent调度技术面临的主要困难.而拍卖机制是一种用来绕过技术和计算困难的主要手段.首先，拍卖可以很好的保护Agent的独立性和私有信息；其次，拍卖可以提供激励机制，使得参与拍卖的Agent都能透露自己对于不同调度方案的真实估价.

自从Myerson[4]提出最优拍卖设计以来，拍卖机制的设计一直是许多研究者关注的研究主题[58].近年来，将组合拍卖机制应用于分布式机器调度领域已引起许多学者的关注，Kutanoglu等[9]证明了组合拍卖与机器调度中经典的拉格朗日松弛算法之间的等价关系，为组合拍卖应用于机器调度问题提供了理论依据；吕赐兴等[10]将基于多Agent的协商策略应用于敏捷生产调度中，利用拉格朗日对偶理论和组合拍卖机制之间的联系，采用拉格朗日乘子作为时段(time slot)的价格，通过对该价格的调整来解决工件之间的冲突，协调可行调度方案的形成过程；Attanasio等[11]对几种不同的价格更新机制进行了比较；Liu等[12]则将机器调度中的不确定因素(如机器故障、工件动态到达等)引入到组合拍卖的模型中，建立了采用拍卖机制解决动态分布式机器调度问题的框架，并通过仿真实验证明了在分布式环境下基于拍卖机制的调度方法优于传统的集中式调度方法；王刚等[7，8]在基于拍卖的多Agent协调调度方面对单机和并行机多Agent调度问题进行了研究，设计了一种基于重复叫价的组合拍卖机制和启发式算法.文献[10-12]均将连续时间离散化，将离散后的时间段作为商品进行拍卖，文献[7，8]采用多回合的拍卖形式.这种离散的多回合的组合拍卖形式，算法的收敛速度与拍卖轮次密切相关，在线计算量大，求解耗时长，在实际操作中有诸多不便.相比之下，本文设计的贪婪机制是单回合的组合拍卖形式且无需将连续时间离散化，机制相对简单，具有很好的实时性.

本文针对制造资源服务平台的需要，研究分布式环境下基于拍卖机制的多Agent资源共享、分配和协调调度的单机调度模型和方法.设计了一种基于单回合拍卖的贪婪机制，从理论上证明了该机制是真实吐露的，并用计算实例对此性质进行了验证，最后通过数值实验对该贪婪机制与线性规划方法的求解效果进行比较，并对结果进行深入分析.

2　基于组合拍卖的多Agent单机调度问题

2.1问题描述

在分布式环境下有客户Agent(i)，i=1，2，...，n，每个客户Agent(i)有一个工件Ji需要加工；一资源Agent拥有一台机器提供加工服务，该机器任一时刻只能加工一个工件.各客户Agent的私有信息不能共享.所有工件的就绪时间均为资源Agent的规划期的初始时刻0，工件Ji的加工时间为pi、交付期为di，在交付期前完工的客户Agent(i)可获得收益vi.为了在规定时间内完工，客户Agent(i)愿意支付一定的费用bi，但不能超过他从该工件获得的收益，即bi≤vi，客户Agent(i)的效用为ui=vi-bi.若工件未在交付期前完工，客户Agent获得的收益为0.本文采用基于需求的投标语言[13]，即客户Agent(i)以〈pi，di，bi〉三元组的形式进行投标.

2.2符号说明

si为工件Ji的开始加工时间；

M为一足够大的正整数；

xi为0-1变量，xi=1表示工件Ji获得所需的资源，否则xi=0；

yij为0-1变量，表示工件Ji和工件Jj加工的先后顺序，yij=1表示工件Ji在工件Jj之前开始加工，yij=0表示工件Ji在工件Jj之后开始加工；

N(i)为客户Agent(i)后第一个在没有工件Ji时可中标，但是有Ji时失标的投标者；

K(i)为排序表中客户Agent(i)后的第一个投标者；

li为客户Agent(i)对其投标加工时段的单位时间投标值，即bi/pi；

Si=〈pi，di〉为客户Agent(i)投标的加工时段，即di之前长度为pi的连续时间段；

θi=〈pi，di，bi〉为客户Agent(i)的类型，表示其愿意为di之前长度为pi的连续时间段支付的费用为bi.以最大化资源Agent收益为目标时，客户Agent(i)在真实吐露的情况下，其愿意为Si支付的最大费用应等于其收益，即bi=vi.

2.3线性规划方法

本文以最大化资源Agent收益为目标，决策调度方案.竞胜标模型为

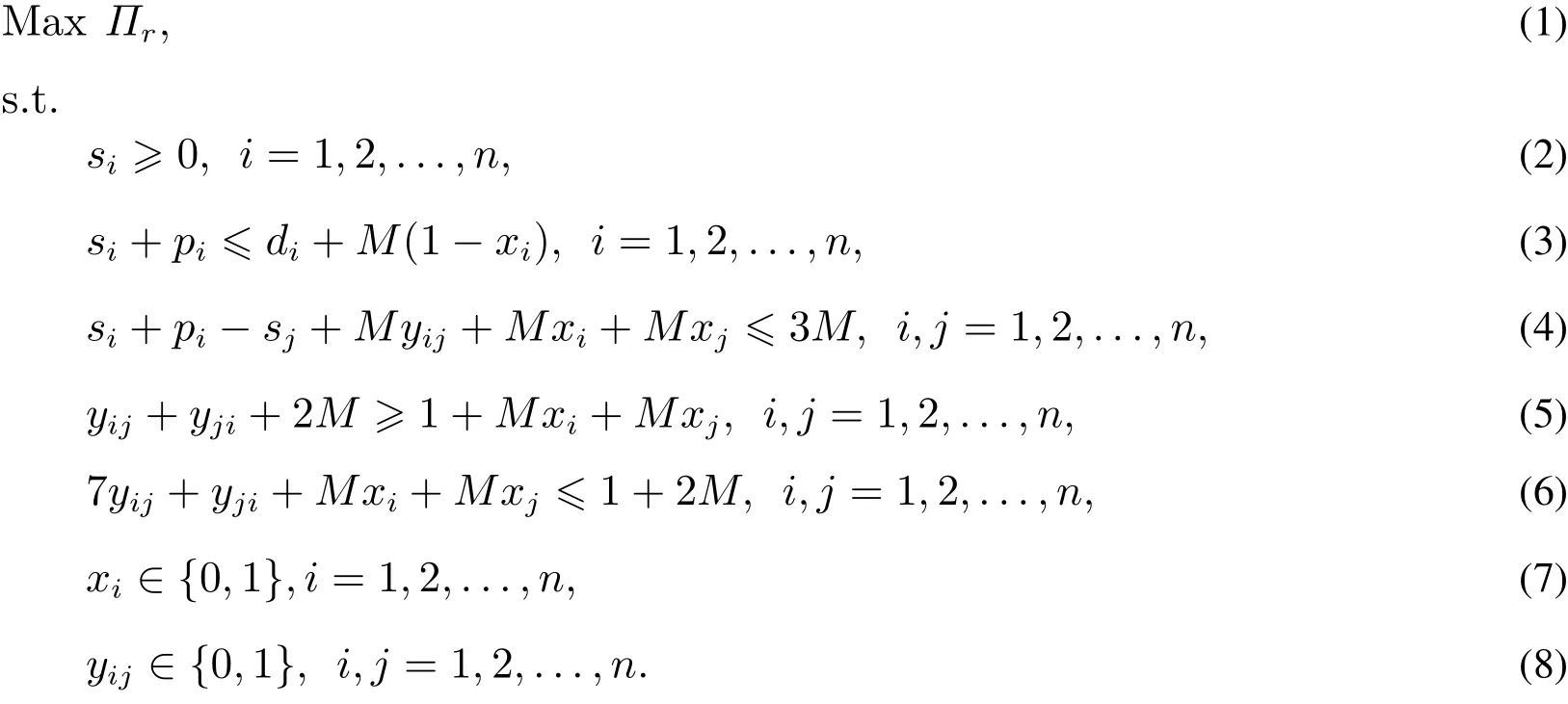
用CPLEX对上述竞胜标模型求解，得最优调度方案，然后中标者以投标价格进行支付.

2.4贪婪机制的设计

贪婪机制包括贪婪分配算法和贪婪支付算法两部分.贪婪分配算法解决竞胜标问题，决策调度方案，贪婪支付算法确定投标者的支付费用.针对分布式环境下多Agent的单机调度问题，本文以资源Agent收益最大为目标，从拍卖的角度出发设计了一种贪婪机制.该机制的工作过程如下：

阶段1收集客户Agent(i)，i=1，2，...，n的投标方案；

阶段2根据投标方案用贪婪分配算法决策机器可用加工时段的调度方案；

阶段3贪婪支付算法计算中标客户Agent的支付费用.

其中贪婪分配算法基于单位时间投标值求解机器可用加工时段的调度方案，具体步骤如下：

步骤1li←bi/pi，i=1，2，...，n，对li按从大到小进行排序，得到的序列记为L；

步骤2t←0；

步骤3依次检查L中的l[i]对应的工件J[i]，将其放在机器可用时段的初始时刻t，若其完工时间t+p[i]超过了交付期则失标；若未超过交付期则中标，且其开始加工时间si为机器可用时段的初始时刻t，t←t+p[i].

贪婪支付算法用于确定客户Agent的支付费用，规则如下：

情形1若xi=0，则客户Agent(i)的支付费用为0；

情形2若xi=1，且存在N(i)，则客户Agent(i)的支付费用为pilN(i)；

情形3若xi=1，且不存在N(i)，则客户Agent(i)的支付费用为pilK(i).

2.5贪婪机制的真实吐露性

为了说明本文设计的机制是真实吐露的，作出下列定义：

定义1真实吐露：机制是真实吐露的，如果对于各客户Agent，投标自己的真实类型时得到的效用大于等于其投标的其他任何类型所得到的效用.

定义2偏好关系≻：客户Agent(i)投标的加工时段为Si=〈pi，di〉，如果工件Ji的加工时间缩短或交付期延后，用表示，其中，则；对于投标类型其中

定义3简单投标者：假设客户Agent(i)的真实类型为θi=〈pi，di，bi〉，客户Agent(i)对Si=〈pi，di〉大于这一加工时段的估价为vi(Si)=bi，即其愿意为Si支付的最大费用为bi，则其对加工时段S的估价为

定义4单调性(针对分配算法)：如果Agent(i)投标θi= 〈pi，di，bi〉时中标，则当其投标=时，i仍中标.即为更少的物品组合投入更多的钱，并不会使中标者失标；反之，为更多物品组合投入更少的钱，也不会使失标者中标.

在客户Agent为简单投标者，分配算法满足单调性的机制中，对于每一个客户Agent的类型θ= 〈p，d，b〉存在一个临界估价bc，当b＞bc时，其中标；当b＜bc时，其失标；当b=bc时，不确定其是否中标.

定义5临界性(针对支付算法)：中标的客户Agent的支付费用等于其临界估价bc.

定义6参与性(针对支付算法)：当客户Agent最终没有完全得到自己投标的加工时段时，其支付费用为0.

文献[14]已证明在投标者为简单投标者的情况下，如果拍卖机制满足单调性、临界性和参与性，则该机制是真实吐露的.

定理1本文设计的贪婪机制是真实吐露的.

证明 本文的客户Agent均为简单投标者.

对“单调性”，设Agent(i)的真实类型为θi=〈pi，di，bi〉，li=bi/pi，投标θi时得到的排序表记为L；对于投标类型，投标时排序表记为 L.假设≻θi，则≥li，Agent(i)在中的位置比在L中的位置靠前.则如果i在排序表L中中标，则i在排序表L中也中标；如果i在排序表L中未中标，i在L中也不可能中标.故贪婪分配算法满足“单调性”.

显然贪婪支付算法满“参与性”.

对于“临界性”，由贪婪支付算法情形2可知，中标者的支付费用恰好等于其可中标时的最小投标值.任何高于lN(i)的单位时间估价使客户Agent(i)位于N(i)之前，如果有一个客户Agentj(li＜ lj＜lN(i))，若j与i冲突，即当i失标时，j会中标，这与N(i)是第一个这样的投标者相矛盾，所以i支付的最高费用为pilN(i)；任何低于lN(i)的单位时间估价会使客户Agent(i)失标，因为N(i)会中标，故i中标时支付的最低费用为pilN(i).所以贪婪支付算法满足“临界性”.另外由于分布式环境下，各客户Agent之间相互不知道对方的投标信息，更不能确定自己的中标情况，而为了保证资源Agent的收益，在不存在N(i)时按贪婪支付算法情形3支付.

3　数值实验

OR-Library是一个汇聚了各种运筹学问题的测试数据的电子数据库，包罗了装箱，背包，选址，网络流，调度，旅行商以及车辆路径等许多经典运筹学问题的测试数据.本文从OR-Library中Scheduling模块下order acceptance and scheduling中选取一些经典单机调度算例进行实验，对线性规划方法与贪婪机制进行比较.所有实验均在MATLAB环境下编写贪婪机制的算法代码，用YALMIP对优化模型建模，调用CPLEX 12.5求解，电脑配置为Intel Core i3 3.10 GHz CPU和4GB RAM GB内存.

3.1线性规划方法不能保证真实吐露

本节设计实验，检验线性规划方法中客户Agent的真实吐露性.实验测试10个算例，每个算例有10个客户Agent，随机选取6个Agent，谎报投标值为收益的95%，90%，80%和75%.真实吐露情况与不同谎报投标值情况下客户Agent的总效用的比较见图1.

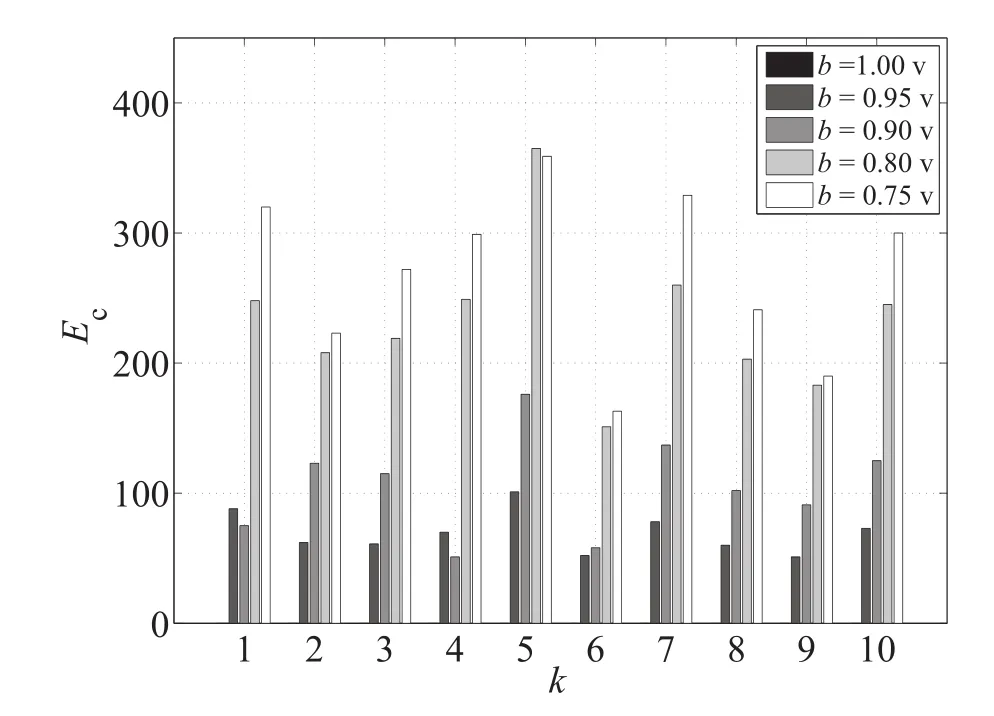
图1　客户Agent总效用(Ec)的比较.Fig.1　Comparison of the client Agent s’utility(Ec).

从图1可知，在投标值等于收益时，客户Agent的效用为0，随着投标值减小，客户Agent的效用呈增加趋势.其中有几组客户Agent的总效用随着投标值减小有小幅下降，这是由于一些客户Agent谎报程度过大而失标，另一些谎报程度小或者无谎报的客户Agent中标，使客户Agent的总效用有所下降.另外，对于每一个客户Agent，谎报投标值为收益的x倍时，中标后效用为(1-x)v，客户Agent为了增加其中标后的效用有动力谎报，故线性规划方法不能保证客户Agent真实吐露.

3.2贪婪机制能保证真实吐露

本节设计一个简单算例，验证贪婪机制的真实吐露性.假设有10个客户Agent，每个客户Agent有1个工件需要竞争机器资源，机器规划期为0～150，各客户Agent的任务描述如表1所示.

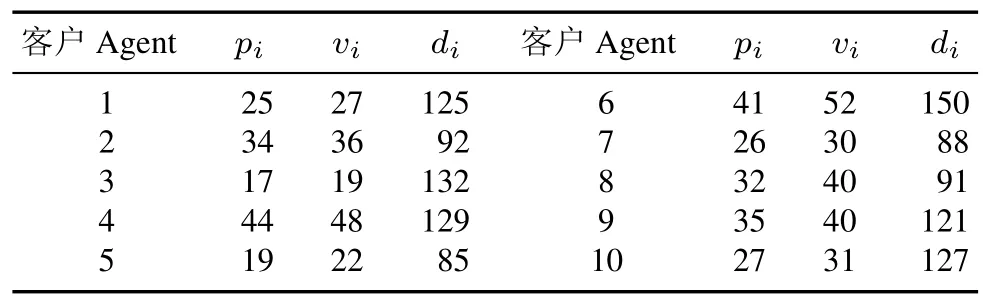
表1　客户Agent的任务描述Table 1　Task description for client Agents

用贪婪机制得到的中标客户Agent为Agent(3)，Agent(6)，Agent(8)，Agent(10)，相应的支付费用为18.4，47.5，37.1和30.9.以客户Agent(3)为例分析，当客户Agent(3)谎报其投标值在[18.4，19]内时，仍中标，但根据贪婪支付算法，其支付费用不变，仍为18.4，这表明降低投标值并不会增加其效用；当客户Agent(3)的投标值小于18.4时，该Agent失标，效用为0.与理论结论相符，客户Agent谎报投标值时其效用不会增加，却有失标的可能.算例分析再次证实本文设计的贪婪机制能够激励各Agent吐露真实信息.

3.3单位时间估价相近时，贪婪机制可保证较好的资源Agent收益

本节设计实验比较贪婪机制与不同谎报估价情况下线性规划方法得到的资源Agent的收益.本实验测试10个工件的情况，各客户Agent的单位时间估价由均匀分布随机生成，根据分布区间的不同(见表2)，分为两组实验数据，每组10个算例.随机选取6个客户Agent，谎报估价为收益的95%、90%、80%和75%，同一组实验中谎报Agent保持不变.进行两组实验，1)客户Agent的单位时间估价在[10，15]上时，贪婪机制分别与4种谎报投标值情形下线性规划方法得到的资源Agent收益、客户Agent总效用和系统收益进行比较，实验结果见图2；2)单位时间估价在[10，30]上时，贪婪机制分别与4种谎报投标值情形下线性规划方法得到的资源Agent收益(Πr)、客户Agent总效用(Fc)和系统收益(Πs)进行比较，实验结果见图3.

表2　客户Agent的单位时间估价的均匀分布区间Table 2　The uniform distribution interval for the unit time valuation of client Agents

从图2(a)与图2(b)可知：当客户Agent的单位时间估价在[10，15]上时，贪婪机制得到的资源Agent收益近似等于谎报到收益的95%左右时线性规划方法得到的资源Agent收益，贪婪机制得到的客户Agent效用等于谎报到估收益的90%左右时线性规划方法得到的客户Agent的效用；从图3(a)与图3(b)可知，当客户Agent的单位时间估价在[10，30]上时，贪婪机制得到的资源Agent收益等于谎报到收益的80%左右时线性规划方法得到的资源Agent收益，贪婪机制得到的客户Agent效用等于谎报到收益的80%左右时线性规划方法得到的客户Agent的效用.

综合图2(a)和图3(a)与图2(b)和图3(b)可知，随着客户Agent投标值的减小，线性规划方法得到的调度方案的资源Agent的收益呈减小趋势，客户Agent的效用呈增加趋势.综合图2(c)和图3(c)知，其系统收益呈递减趋势.这是由于一些原本中标的客户Agent谎报程度过大而失标，另一些单位时间估价低的客户Agent中标所致.

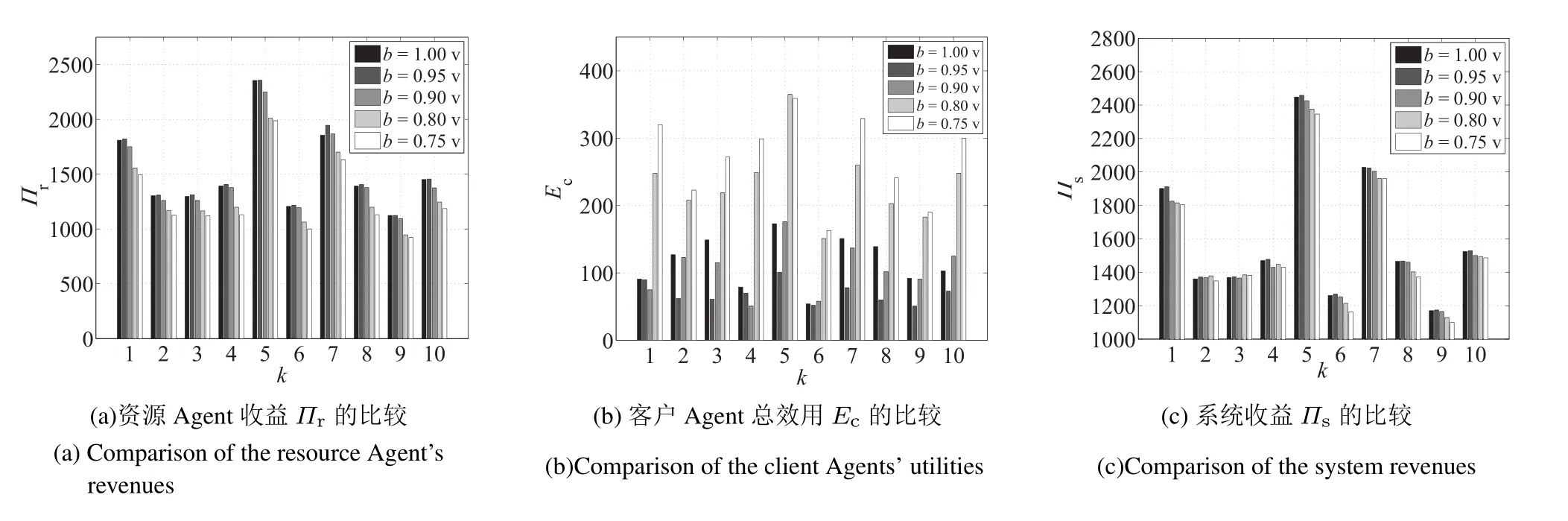
图2　第一组实验结果(k为仿真算例编号)Fig.2　The experimental results of first group(k is the simulation example number)

对比两组实验，单位时间估价区间较小，即当客户Agent的单位时间估价相近时，贪婪机制得到的调度方案中，在保证客户Agent合理的效用时，使资源Agent获得较好的收益.因此在线性规划方法无法保证客户Agent真实吐露的情况下，采用贪婪机制可以得到较好的效果.当客户Agent的单位时间估价相差较大时，采用贪婪机制得到的调度方案中，中标客户Agent的支付费用与其收益相差较大，资源Agent的收益损失变大，但是此时客户Agent的效用(Ec)较大，这样可以鼓励更多的客户Agent参与投标，实现资源的优化配置.

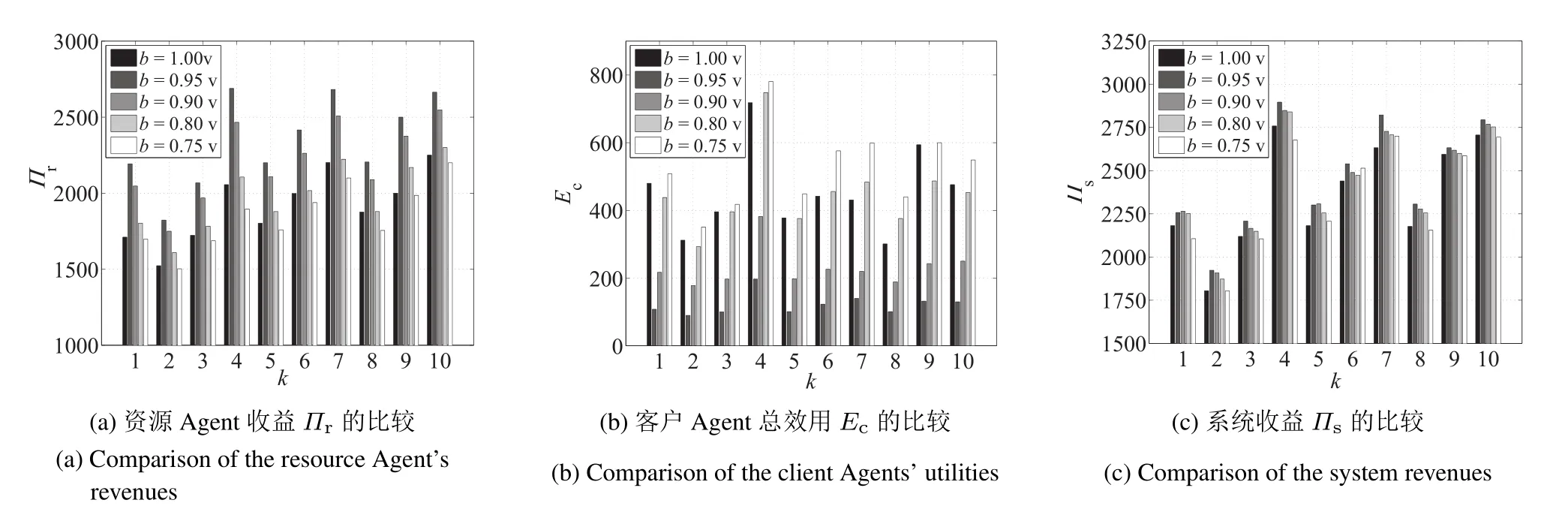
图3　第二组实验结果(k为仿真算例编号)Fig.3　The experimental results of second group(k is the simulation example number)

3.4两种机制的求解效果

本节设计实验对两种机制的系统收益，机器加工时段的单位时间收益和求解时间进行比较.本实验分别测试需要加工的工件数为10，15，20和100个工件4种情况，每种情况10个算例.两种机制下4种情况的10个算例的最终调度方案的平均中标工件数、平均机器利用率、平均系统总收益、平均单位时间收益和平均求解时间如表3所示.

表3　贪婪机制与线性规划方法求解结果比较Table 3　Comparison between the Greedy Mechanism and Linear Programming

从表3可以看出，贪婪机制得到的系统收益近似于最优系统收益；贪婪机制得到的最终调度方案使得机器加工时段的单位时间收益高于线性规划方法得到机器单位时间收益；随着工件数增多，线性规划方法的求解时间显著增加，且对于15个工件的情况，由于计算量太大，只有1个算例在有效时间内求解成功，对于20个和100个工件2种情况，全部算例在有效时间内无法得到调度方案，而贪婪机制对4种情况均在1 s内得到了全部算例的调度方案.

4　结束语

针对分布式环境下的多Agent单机调度问题，本文从拍卖的角度出发，设计了一种贪婪机制，该机制包括贪婪分配算法和贪婪支付算法两部分，贪婪分配算法解决竞胜标问题，贪婪支付算法以第二价格支付的形式确定中标者的支付费用，该机制能够保证真实吐露，且机制规则简单，方便执行.实验表明，本文设计的贪婪机制能够激励客户Agent真实吐露；在各客户Agent对机器加工时段的单位时间估价相近时，该机制可以保证资源Agent较好的收益；对大规模问题，该机制能够快速得到使系统总收益接近最优的调度方案.本文的研究还可以进一步深入，在竞胜标问题中考虑客户优先权和留住重要客户等调度指标，推广到平行机调度问题等.这些都有待于进一步研究.

[1]YusufYY，SarhadiM，GunasekaranA.Agilemanufacturing：Thedrivers，conceptsandattributes.InternationalJournalofProduction Economics，1999，62(1/2)：33-43.

[2]王康周，江志斌，李娜，等.服务型制造综合资源计划体系研究.工业工程与管理，2011，16(3)：113-120. Wang K Z，Jiang Z B，Li N，et al.A framework for resource planning of service-oriented manufacturing.Industrial Engineering and Management，2011，16(3)：113-120.(in Chinese)

[3]李伯虎，张霖，王时龙，等.云制造：面向服务的网络化制造新模式.计算机集成制造系统，2010，16(1)：1-7. Zhang B H，Zhang L，Wang S L，et al.Cloud manufacturing：A new service2oriented networked manufacturing model.Computer Integrated Manufacturing Systems，2010，16(1)：1-7.(in Chinese)

[4]Myerson R B.Optimal auction design.Mathematics of Operations Research，1981，6(1)：58-73.

[5]汪定伟.网上集中采购的捆绑-组合拍卖机制设计.系统工程学报，2011，26(6)：809-816. Wang D W.Mechanism design of hybrid bundling and combination auction for centralized E-procurement.Journal of Systems Engineering，2011，26(6)：809-816.(in Chinese)

[6]饶从军，赵勇.可分离物品多属性采购拍卖的最优机制.系统工程学报，2012，27(1)：88-98. Rao C J，Zhao Y.Optimal mechanism of multi-attribute procurement auction for divisible goods.Journal of Systems Engineering，2012，27(1)：88-98.(in Chinese)

[7]王刚，陈秋双，杜玉泉等.基于组合拍卖的多主体单机调度问题.计算机集成制造系统，2013，19(1)：106-113. Wang G，Chen Q S，Du Y Q，et al.Multi-Agent single machine scheduling based on combinatorial auction.Computer Integrated Manufacturing Systems，2013，19(1)：106-113.(in Chinese)

[8]王刚，陈秋双.加工时间可控的多主体单机调度问题研究.计算机集成制造系统，2013，19(9)：2187-2192. Wang G，Chen Q S.Multi-Agent scheduling with controllable processing times.Computer Integrated Manufacturing Systems，2013，19(9)：2187-2192.(in Chinese)

[9]Kutanoglu E，Wu S D.On combinatorial auction and Lagrangean relaxation for distributed resource scheduling.IIE Transaction，1999，31(9)：813-826.

[10]吕赐兴，朱云龙，尹朝万，等.基于多Agent的敏捷生产调度中的协商策略.计算机集成制造系统，2006，12(4)：579-584. LüC X，Zhu Y L，Yi C W，et al.Negotiation policy for multi-Agent based agile production scheduling.Computers Integrated Manufacturing Systems.2006.12(4)：579-584.(in Chinese)

[11]Attanasio A，Ghiani G，Grandinetti L，et al.Auction algorithms for decentralized parallel machine scheduling.Parallel Computing，2006，32(9)：701-709.

[12]Liu Ning，Abdelrahman M A，Ramaswamy S.A complete multiagent framework for robust and adaptable dynamic job shop scheduling.IEEE Transactions on Systems，Man and Cybernetics，2007，37(5)：904-916.

[13]Parkes D C，Ungar L H.An Auction-based Method for Decentralized Train Scheduling//Proceedings of the 5th International Conference on Autonomous Agents.New York：ACM，2001：43-50.

[14]Lehmann D，O’Callaghan L I，Shoham Y.Truth revelation in approximately efficient combinatorial auctions.Journal of the ACM，2002，49(5)：577-602.

Multi-Agent single machine scheduling based on truthful greedy mechanism

Jiang Xue，Quan Xiongwen，Chen Qiushuang
(College of Computer and Control Engineering，Nankai University，Tianjin 300071，China)

This paper proposes a greedy mechanism based on combinatorial auction to solve the distributed multi-Agent scheduling problem.The greedy mechanism includes a greedy allocation algorithm and a greedy payment algorithm，where the former solves the winner determining problem with the goal of maximizing the revenues of source Agent and the latter determines the minimum fees that winners should pay in the form of second price payments.It is proved that the mechanism is truthful，and a series of numerical examples are used to illustrate the feasibility and validity of the greedy mechanism.Furthermore，a simulation experiment is done to compare the effectiveness of the greedy mechanism and the linear programming method.The result showsthatthegreedymechanismcansolvelarge-scaleschedulingproblemswithlesscomputationaltimewhile achieving near optimal revenues for the system.

multi-Agent single machine scheduling；combinatorial auction；truthful；greedy mechanism

TH166

A

1000-5781(2016)03-0423-08

10.13383/j.cnki.jse.2016.03.013

姜雪(1992-)，女，河南新乡人，硕士生，研究方向：系统优化与调度，Email：jiangxue s@163.com；

全雄文(1979-)，男，浙江永嘉人，博士，讲师，研究方向：系统优化与调度，Email：quanxw@nankai.edu.cn；

陈秋双(1966-2015)，女，河北冀州人，教授，博士生导师，研究方向：系统优化与调度，Email：chenqs@nankai.edu.cn.

2014-12-30；

2015-11-30.

国家自然科学基金资助项目(71172071；61403213)；高等学校博士学科点专项科研基金资助项目(201200311100-36).