基于演化博弈的新型农产品批发模式构建问题探讨

2016-10-11姚冠新教授通讯作者边晓雨江苏大学管理学院江苏镇江2203扬州大学江苏扬州225009

商业经济研究 2016年17期

■ 姚冠新　教授　何　勇　通讯作者　边晓雨（、江苏大学管理学院　江苏镇江　2203　2、扬州大学　江苏扬州　225009）

■ 姚冠新1、2教授何勇1通讯作者边晓雨1（1、江苏大学管理学院江苏镇江2120132、扬州大学江苏扬州225009）

本文针对新型农产品物流园区模式构建过程中多方主体参与的问题，建立了农户、批发商、地方政府的三方演化博弈模型。引入政府补贴、收益、合作投资、产业升级成本、风险成本、超额收益等变量，对博弈模型进行求解，并对演化结果相关变量进行灵敏度分析，从而得出对新模式构建过程中各主体行为以及农产品物流从传统批发模式向一体化、产业化运作模式推进过程的相关对策与建议。

农产品物流模式物流园区三方演化博弈

引言

当前我国以批发商为主导的农产品物流模式仍然存在着诸多缺陷和不足。近年，我国也出现了以批发市场为核心的物流园区模式，并受到相关学者关注，如张京敏（2015）通过对比中外农产品物流发展模式，提出切合中国实际情况的本土农产品物流发展新思路：即形成以农产品物流园区为核心，联合农村合作社，通过一定的协议，相互合作、共担风险的中国农产品物流的未来发展模式。

当前，对于新型农产品批发物流园区模式有了一些研究，但对此模式下相关主体关系的研究依然很少。因此，本文针对近年来我国新兴起的农产品物流园区模式以及其构建过程出现的多方主体参与的现象，构建三方演化博弈模型，研究传统的批发商主导模式向新的批发商主导的物流园区模式演进过程。关于三方演化博弈问题，也有部分学者在生态链企业稳定性等方面进行过相关研究，本文参考上述学者的三方博弈模型，研究了新兴农产品物流模式的构建演化过程，以期为农产品产业化、集成化、一体化物流模式发展提供一些建议。

模型构建与分析

（一）模型基本假设

假设1：参与人假设模型中有三个参与人，分别为当地政府、批发商、农户合作组织，三方均满足“理性经济人”假设，在客观条件的约束下都会追求自身利益的最大化。在一个“自然”环境中，各主体均具有限理性且具有较强学习模仿能力，可以通过对比其他主体策略及收益情况调整策略。

假设2：参与人效益假设通过多主体参与的农产品物流模式构建，地方政府可增加财政收入和实现社会效益；批发商可以通过新型农产品产业链模式获得更大的经济效益，并可获得政府更多的支持和税收等政策上的优惠；农户合作组织可以提高农产品生产技术获得更多、更稳定的经济收入。

假设3：行动方案假设政府的行动方案有两种，即对新型农产品物流产业园区模式构建给予政策上的支持和不支持两种态度；对于批发商来说，可以积极构建农产品物流园区和消极构建两种态度；对于农户合作组织来说，可以选择与批发商积极合作进行技术升级也可以选择不合作。

当地政府选择支持构建的概率为x，则选择不支持的概率为1-x；批发商选择积极构建的概率为y，则选择消极构建的概率为1-y；农户合作组织选择合作的概率为z，则选择不合作的概率为1-z。

表1　新模式构建时三方主体收益矩阵

表2　雅克比矩阵均衡点的局部稳定性

（二）模型构建

当地政府的相关损益：当采取支持构建策略时，当地政府需要在政策上对批发商、农户给予支持，比如税收优惠或者补贴等其它支持，这里统一界定为一项成本费用H1、H2，当政府采取不支持的策略时就无需向批发商支付任何费用，此时获得额外收益为U2。新模式构建起来会带给政府额外收益U1。

批发商的相关损益：若当地政府支持构建便可得到资金支持，政府不支持则为0；批发商若选择积极构建物流园区需支出成本为C1，消极构建不需要支付额外成本，没有政府补贴支持；在农户选择不合作的情况下消极构建可获得的收益为π1，在农户合作情形下选择积极构建可获得超额收益为Δπ1，同时双方会面临F的风险成本，批发商承担风险系数为γ，农户不合作时积极构建时超额收益系数为β1，农户合作时选择消极构建超额收益为0。

农户合作组织相关损益：若当地政府支持构建可从政府得到H2的资金支持，政府不支持则为0；农户若选择合作需支出技术升级成本C2，不合作不需要支付额外成本，没有政府补贴支持；在批发商选择消极构建的情形下选择不合作可获得收益为π2，在批发商选择积极构建的情形下选择合作可以获得超额收益Δπ2，同时双方面临共担的风险成本F，农户承担的风险系数为（1-γ），批发商消极构建时选择合作时超额收益系数为β2，批发商积极构建时选择不合作超额收益为0。

三方主体收益矩阵如表1所示。

U11表示当地政府采取策略支持时的期望收益，则：

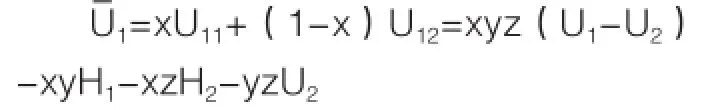
可得，当地政府采取支持策略比例的动态复制方程为：

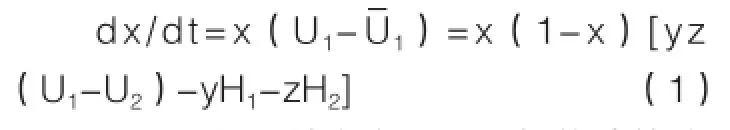
同理可得，批发商采取积极构建策略比例的动态复制方程：

同理，农户采取合作策略比例的动态复制方程为：

令dx/dt=0，dy/dt=0，dz/dt=0得出14个均衡点分别为N0（0，0，0），N1（1，0，0），N2（0，1，0），N3（0，0，1），N4（1，0，1），N5（1，1，0），N6（0，1，1），N7（1，1，1），

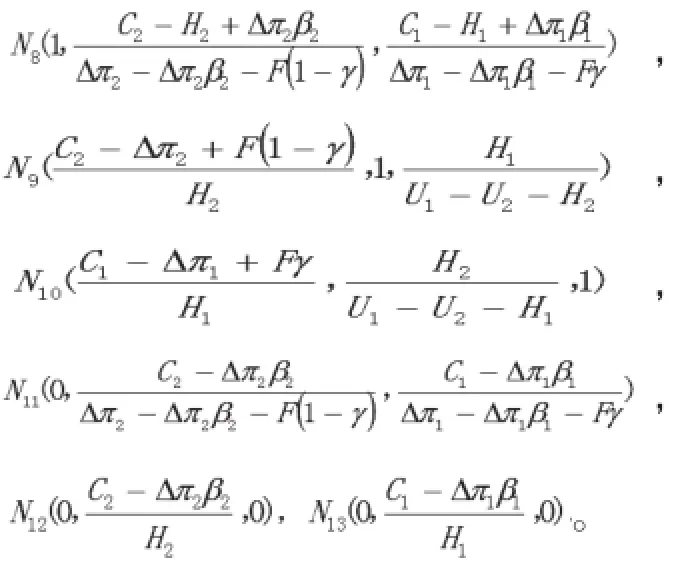
由微分方程（1）、（2）、（3）得出雅克比矩阵为J：

图1　均衡点局部稳定性及进化路径分析

演化路径分析

根据模型的假设，当地政府采取支持、批发商采取积极构建、农户采取合作策略时，博弈三方的合作能够达成，新模式得以构建并运行，此时三方获得的收益（直接收益+间接收益）大于其采取对应策略的成本U1＞H1+H2，Δπ1+H1＞C1+Fγ，Δπ2+H2＞C2+F（1-γ）。任一初始点及其演化后的点在三维空间内才具有意义。

1.若U1-U2＜H1+H2，Δπ2＜Δπ2β2+ F（1-γ），Δπ1＜Δπ1β1+ Fγ：

即意味着当农户和批发商积极合作时，当地政府采取支持的最终受益比采取不支持的最终受益少，显然此时“不支持”是当地政府的占优策略；当批发商坚决采取积极构建时与农户达成合作一致构建起新模式产生的最终受益小于因农户不合作而未构建起新模式的最终收益；同样当农户坚决采取合作时批发商采取积极时农户最终收益小于因批发商消极构建而未构建起新模式的最终收益。现实意义是当地政府、批发商和农户积极合作的积极性受到风险成本过高因素的打击而丧失积极性。导致博弈方长期博弈结果偏离｛支持，积极，合作｝。如此是不利于博弈各方之间合作构建新模式，因此不做详细讨论。

2.若U1-U2＞H1+H2，Δπ2＞Δπ2β2+ F（1-γ），Δπ1＞Δπ1β1+ Fγ：

演化博弈中存在采取不合作（不支持、消极）策略的博弈方，而其他主体选择合作（积极、支持）情形下获得的超额收益足以补偿其直接成本，即Δπ1＞C1+ Fγ，Δπ2＞C2+ F（1-γ），Δπ1β1＞C1，Δπ2β2＞C2，点N8、N9、 N10、N11、N12、N13不在演化博弈的三维空间内dx/dt=0，x=0，x=1是x的稳定状态，其中x=1是进化稳定策略，同理是y=1，z=1是进化稳定策略，均衡点为进化稳定点，即｛支持，积极构建，合作｝为进化稳定策略。因此只要超额收益足以弥补风险及成本，长期博弈结果为｛支持，积极构建，合作｝。

演化博弈中存在采取不合作（不支持、消极）策略的博弈方，而其他主体选择合作（积极、支持）情形下获得的超额收益不足以补偿其直接成本Δπ1β1+H1＜C1，Δπ2β2+H2＜C2，Δπ1＜C1+ Fγ，Δπ2＜C2+F（1-γ），Δπ1β1＜C1，Δπ2β2＜C2时点N11、N12、N13不在演化博弈的三维空间内。点N8在面S1=｛x，y，z（x=1，0＜y＜1，0＜z＜1）｝上，点N9在面S2=｛ x，y，z （0＜x＜1，y=1，0＜z＜1）｝上，点N10在面S3=｛ x，y，z（0＜x＜1，0＜y＜1，z=1）｝上，借助雅克比矩阵J对均衡点的局部稳定性进行分析（见表2）。

由表2可知均衡点（1，1，1）为进化稳定点，均衡点为鞍点。进化路径如图1所示。

当Δπ1＞C1+ Fγ，Δπ2＞C2+F（1-γ），Δπ1β1＞C1，Δπ2β2＞C2时，由图1可知如果博弈三方的初始状态落在区域Ⅰ、Ⅱ、Ⅲ内，博弈行为将演化到点，即演化到｛支持，积极，合作｝的策略；演化到点的可能性与区域Ⅰ、Ⅱ、Ⅲ的面积有关，面积越大演化到点的可能性越大。影响区域Ⅰ、Ⅱ、Ⅲ面积的参数的方向与博弈进化的方向一致，由图1可知区域Ⅰ、Ⅱ、Ⅲ的面积S为：

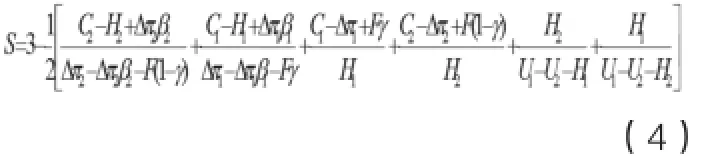
演化博弈结果分析

演化博弈中存在采取不合作（不支持、消极）策略的博弈方，而其他主体选择合作（积极、支持）情形下获得的超额收益足以补偿其直接成本，即Δπ1＞C1+ Fγ，Δπ2＞C2+F（1-γ），Δπ1β1＞C1，Δπ2β2＞C2时｛支持，积极，合作｝为进化稳定策略。因此只要超额收益足以补偿其直接成本时博弈各方主体间的长期博弈结果为｛支持，积极，合作｝。

演化博弈中存在采取不合作（不支持、消极）策略的博弈方，而其他主体选择合作（积极、支持）情形下获得的超额收益不足以补偿其直接成本即Δπ1β1+H1＜C1，Δπ2β2+H2＜C2，Δπ1＜C1+ Fγ，Δπ2＜C2+F（1-γ），Δπ1β1＜C1，Δπ2β2＜C2时，由式（4）可知影响各博弈主体间合作构建新模式的参数包括合作超额收益Δπi、Δπiβi、Ui，成本Ci、Hi、F（i=1，2），收益系数风险系数γ、β。根据式（4）分析各参数对新模式构建的影响：

新模式构建后的超额收益：

因此S为Δπi的增函数，随着新的农产品批发模式的构建所得超额收益Δπi的增加，S逐渐增大，博弈演化到点N7（1，1，1）的可能性增大。

新模式给政府带来的效益Ui：

因此S为U1的增函数，随着新的农产品批发模式的构建政府采取支持策略所得效益U1的增加，S逐渐增大，博弈演化到点N7（1，1，1）的可能性增大。

因此S为U2的减函数，随着新的农产品批发模式的构建政府采取不支持策略所得效益U2的增加，S逐渐减小，博弈演化到点N7（1，1，1）的可能性减小。

构建新模式的成本Ci：

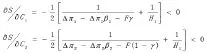
因此S为Ci的减函数，随着新的农产品批发模式的构建所需成本Ci的增加，S逐渐减小，博弈演化到点N7（1，1，1）的可能性减小。

当地政府补贴Hi：

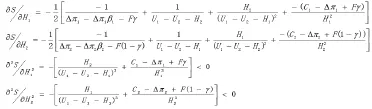
当H1→0时，H1→U1-U2时，＜0，在（0，U1-U2）递减，因此存在H1，使

同理可得，在（0，U1-U2）内存在H2，使

那么，在（0，U1-U2）上一定范围内随着当地政府补贴的增大，S增大，后来随着其增大而减小，H1+H2＜U1-U2。

新模式下批发商与农户的风险成本F：

因此S为F的减函数，随着新的农产品批发模式的构建批发商与农户间合作风险成本F的增加，S逐渐减小，博弈演化到点N7（1，1，1）的可能性减小。

新模式未构建，但批发商、农户一方积极合作时的超额收益系数βi：

因此S为βi的减函数，随着新模式未构建时批发商、农户一方积极合作的超额收益系数βi增大，S逐渐减小，博弈演化到点N7（1，1，1）的可能性减小。

新模式构建时批发商与农户间的风险分配系数γ：

分配系数γ对S的影响与其它多个系数相关，单调性在此难以细化深入具体分析，因此省略。

由上述分析可知，通过提高新模式构建后带给批发商、农户的超额收益以及当地政府的效益，降低当地政府不支持时的效益以及批发商和农户的构建成本，确定最佳的政府补贴，减小新模式下批发商与农户间的合作风险及仅一方积极合作时积极一方的超额收益系数，确定最佳的风险分配系数能够促进新农产品批发模式构建的各个主体积极合作支持，从而保障建立统一的农产品批发模式。

从上述研究可以看出，在现有批发商主导的农产品物流模式下要想建立起新型批发商主导的农产品物流园区模式，需要当地政府、批发商、农户多方共同配合积极合作，涉及构建成本、政府补贴、新模式运行效益等多方面问题，对此从以上分析出发，笔者提出相关建议。

当地政府在新模式的构建过程中起着促进和推动的作用，因新模式下物流园区的构建需要大量的成本，政府给予批发商及农户一定补贴，新模式构建起来之后，能给当地政府带来经济或其它效益，在一定范围内增加补贴力度有利于促进批发商、农户积极合作建设，但是过高的补贴容易导致出现“搭顺风车”的现象以及政府得不偿失的局面。因此，适度的补贴才是理性促进批发商和农户积极合作构建新模式的举措。

批发商在新模式下依然处于主导地位，是新模式的最大受益者，而新模式的物流园区建设也需要批发商付出相当的成本，同时在与农户间的合作关系中也承担着合作风险，因此设法使新模式下批发商的收益显著提高，可通过政府补贴，充分利用新的模式下的技术优势探讨合理的交易合作机制，更准确地预测市场需求以充分降低风险以及交易等成本，才能促使批发商以更强的动力构建新模式，并发挥出新模式的优势。

农户是农产品的输出者，是生产主体，一直以来农户在我国农产品交易过程当中多处于弱势地位。在新模式中，通过政府协调批发商与农户合作组织间进行更为紧密的对接合作，农户地位得到提升，但是农户需要进行产业技术升级，以向批发商提供更加优质、产量稳定的农产品，因此为减少农户参与合作的阻力，政府需为农户提供技术支持以及产业技术升级的补贴，促进监督与批发商间良好的合作以降低风险，保障农户在合作过程中的切实利益。

1.刘联辉，文珊.我国农产品物流系统模式革新趋势及其构筑策略［J］.农村经济，2006（5）

2.贺峰.中国农产品物流模式构建：基于批发市场的研究［J］.农业技术经济，2006（5）

3.寇平君，卢凤君.构建我国农产品市场流通模式的战略性思考［J］.农业经济问题，2002（8）

4.盛革.我国农产品现代流通服务体系的协同优化设计［J］.管理评论，2009（8）

5.赵晓飞.我国现代农产品供应链体系构建研究［J］.农业经济问题，2012（1）

6.李建平，王吉鹏，周振亚等.农产品产销对接模式和机制创新研究［J］.农业经济问题，2013（11）

7.张京敏，王如晖.中国农产品物流模式探讨—基于中外农产品物流模式的对比分析［J］.热带农业工程，2015，39（1）

8.杨军，葛孚桥.现代农产品物流体系建设与运行的财政支持政策探讨［J］.生态经济，2011（3）

9.周甜甜，王文平.基于演化博弈论的生态产业链稳定性研究［J］.科技与经济，2014，27（1）

10.吴瑞明，胡代平，沈惠璋.流域污染治理中的演化博弈稳定性分析［J］.系统管理学报，2013，22（6）

11.翟丽丽，柳玉凤，王京等.软件产业虚拟集群企业间信任进化博弈研究［J］.中国管理科学，2014（12）

12.魏芳芳，陈福集.网络虚假信息中政府、企业和公民三者的进化博弈行为分析［J］.运筹与管理，2012，21（6）