一类带参数的Hilbert型积分算子及其应用

陈广生，唐慧羽，韦银幕，覃茂华

(广西现代职业技术学院建筑与信息工程系， 广西　河池　547000)



一类带参数的Hilbert型积分算子及其应用

陈广生，唐慧羽，韦银幕，覃茂华

(广西现代职业技术学院建筑与信息工程系， 广西河池547000)

在广义区间(a,b)上给出了一个含有参数的Hilbert型奇异积分算子T，研究了它的界及其涉及内积的等价形式;作为应用，研究它对一类偏微分方程解的估计．

Hilbert型奇异积分算子；Hilbert型不等式；算子范数；内积；Hölder不等式

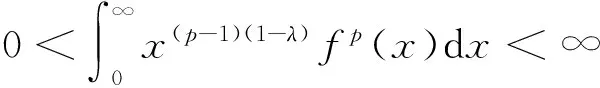
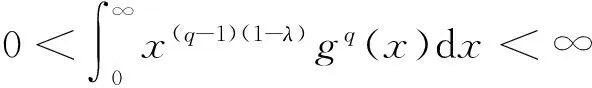
则下面的Hilbert型积分不等式[1]成立：

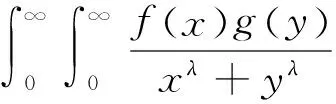
(1)

(2)

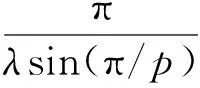
本文拟在广义区间(a,b)上，建立一个新的Hilbert型奇异积分算子，并讨论其有界性问题及一些相关结果．作为应用，给出了一类偏微分方程解的估计．

1　主要结果

首先给出Hilbert型奇异积分算子：

(3)

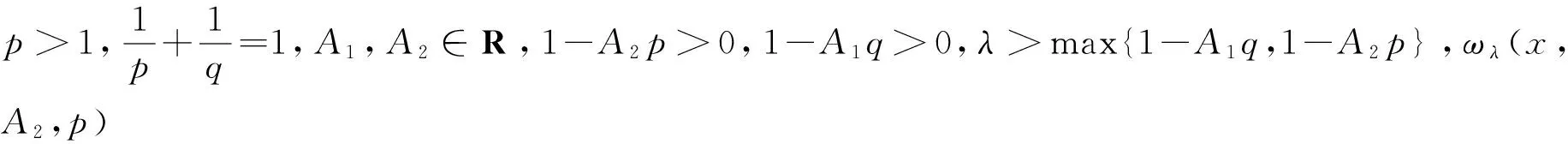
(4)

(5)

则有

ωλ(x,A2,p)

(6)

ωλ(y,A1,q)

(7)

证明作变换u=yλ/xλ，则有

根据文献[10]中广义的算术几何不等式得到

因此有

ωλ(x,A2,p)

同理可证明

ωλ(y,A1,q)

(8)

证明设

g(y)=y(p-1)(λ-1)+p(A1-A2)×

这里y∈(a,b).由文献[10]中的Hölder不等式，得

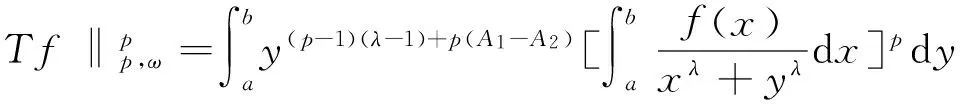
根据引理1中的结果

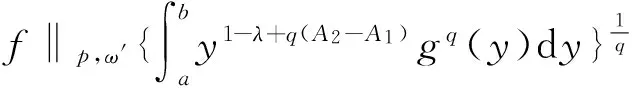
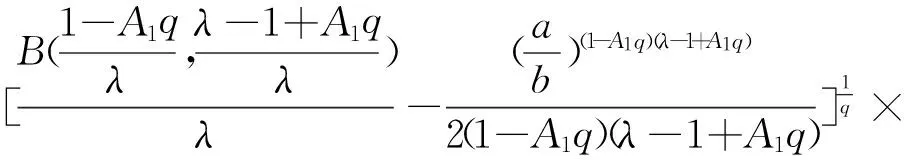
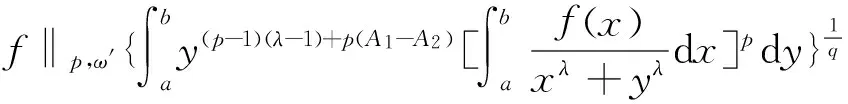
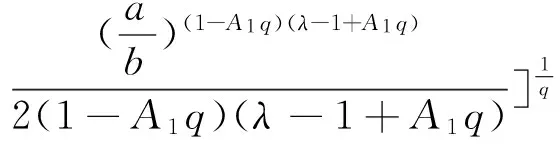
从而得到

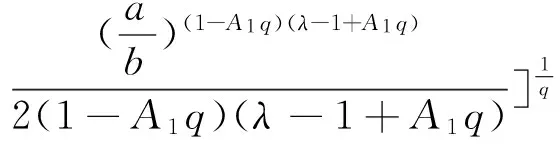
因此(8)式成立.

2　等价形式及特例

假定函数f(x)、g(x)在(a,b)上是非负可测的，将内积(f,g)定义为

‖f‖p,ω′‖g‖q,ω″

(9)

证明假设ω=x(p-1)(λ-1)+p(a-b)，利用Hölder不等式及(8)式，有

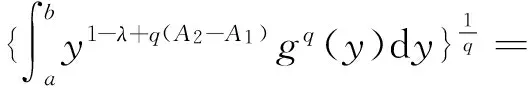
‖f‖p,ω′‖g‖q,ω″

所以(9)式成立.由(9)式可导出(8)式，故(9)式与(8)式等价.

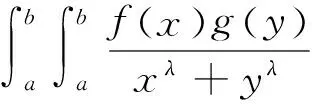
(10)

(11)

这里

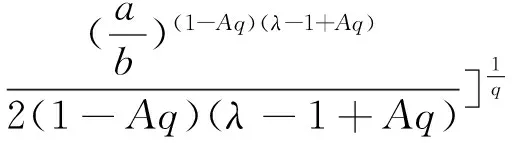
证明在定理1和推论1中，令A1=A2=A，便可得到(10)式和(11)式.

3　偏微分方程解的估计

考虑下面的偏微分方程：

(12)

满足条件:

ux(x,b)=0a≤x≤b

(13)

u(a,y)=0,a≤y≤b

(14)

由(12)式和(13)式得

因此

(15)

由(14)、(15)式得

(16)

根据(16)式，得到

(17)

由于a≤x≤b，a≤y≤b， 根据(17)式，得

(18)

应用(10)式，根据(18)式，得到

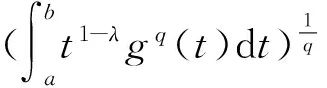
即有

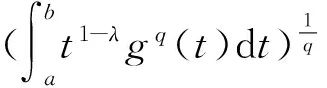
[1]杨必成. 关于一个推广的Hardy-Hilbert不等式[J].数学年刊，2002，23A(2)：247-254.

[2]HARDYGH,LITTLEWOODJE,POLYAG．Inequalities[M]．Cambridge：CambridgeUrav．Press，1952．

[3]MITRINOVICDS，PECARICJE，FINKAM.Inequalitiesinvolvingfunctionsandtheirintegralsandderivatives[M]．Boston：KluwerAcademicPublishers，1991．

[4]XIEZT，ZENGZ．AHilbert-typeintegralinequalitywhosekernelisahomogeneousformofdegree-3[J]．JournalofMathematicalAnalysisandApplications，2008，339(1)：324-331．

[5]杨必成．关于一个推广的具有最佳常数因子的Hilbert类不等式及其应用[J]．数学研究评论，2005，25(2)：341-346.

[6]洪勇．一个新的Hilbert重积分不等式[J]．西南师范大学学报(自然科学版)，2005，30(4)：594-599．

[7]YANGBC．Onthenormofanintegraloperatorandapplication[J]．JournalofMathematicalAnalysisandApplications，2006，32(1)：182-192．

[8]洪勇．关于Hardy-Hilbert积分不等式的全方位推广[J]．数学学报，2001，44(4)：619-626．

[9]洪勇.一类Hilbert型奇异积分算子的范数及其应用[J].西南师范大学学报(自然科学版)，2010，35(5)：40-44.

[10]匡继昌．常用不等式[M]．济南：山东科学技术出版社，2004.

(责任编辑穆刚)

A Hilbert’s type singular integral operator with some parameter and its application

CHEN Guangsheng, TANG Huiyu, WEI Yinmu, QIN Maohua

(Department of Construction and Information Engineering, Guangxi Modern Vocational Technology College, Hechi Guangxi 547000, China)

In this paper，we define a Hilbert type singular multiple integral operator with parameters，and from the generalized interval betweenaandb, the boundary and norm of T and the equivalent forms are studied．As their applications, we consider estimates for the solutions of a class of partial differential equations．

Hilbert’s type singular integral operator；Hilbert’s type inequality；norm of operator; inner product ；Hölder’s inequality

2016-02-13

广西教育厅科学研究项目(KY2015YB468).

陈广生(1979—)，男，广西北流人，副教授，硕士，主要从事解析不等式、小波分析方面的研究.

O178

A

1673-8004(2016)05-0015-04