三星型活塞式压缩机曲轴配重优化问题研究
2016-10-10汤长根何芝仙韩燕林
汤长根,李 震,何芝仙,韩燕林
(1.安徽工程大学机械与汽车工程学院, 安徽 芜湖 241000; 2.安徽工程大学力学重点实验室, 安徽 芜湖 241000)
三星型活塞式压缩机曲轴配重优化问题研究
汤长根1,李震1,何芝仙2,韩燕林1
(1.安徽工程大学机械与汽车工程学院, 安徽芜湖241000; 2.安徽工程大学力学重点实验室, 安徽芜湖241000)
三星型压缩机是一种动力学性能良好的新型活塞式压缩机,其主传动系统由1个主连杆、2个副连杆并联构成的主副连杆机构组成.本文针对三星型压缩机的曲轴配重优化问题建立了其曲轴配重优化设计的数学模型,并以曲轴轴颈中心响应振幅最小作为目标函数,将曲轴配重的质量作为设计变量,利用ADAMS软件中的“优化设计”模块求出曲轴配重的最优解.优化结果表明:曲轴配重的大小对三星型压缩机的动力学性能有十分显著的影响,优化后最优点的目标值比原设计点的目标值降低了17. 02﹪.三星型压缩机的曲轴配重对改善其动力学性能十分必要.
主副连杆机构;优化;ADAMS软件;振幅
三星型压缩机是笔者自主设计研发的一种动力学性能良好的新型活塞式压缩机[1].此压缩机的主传动系统由1个主连杆和2个副连杆并联构成的主副连杆机构组成,所有的连杆与气缸呈120o分布于同一个水平面内,如图1所示.由于三星型压缩机3个气缸工作时间间隔相等,其运动部件的往复力矩理论上为0,且惯性力能够得到较好的平衡.该型压缩机曲轴是否需要配重?如需配重,最优配重质量为多少?这是该型压缩机设计要解决的关键问题之一[2-4].
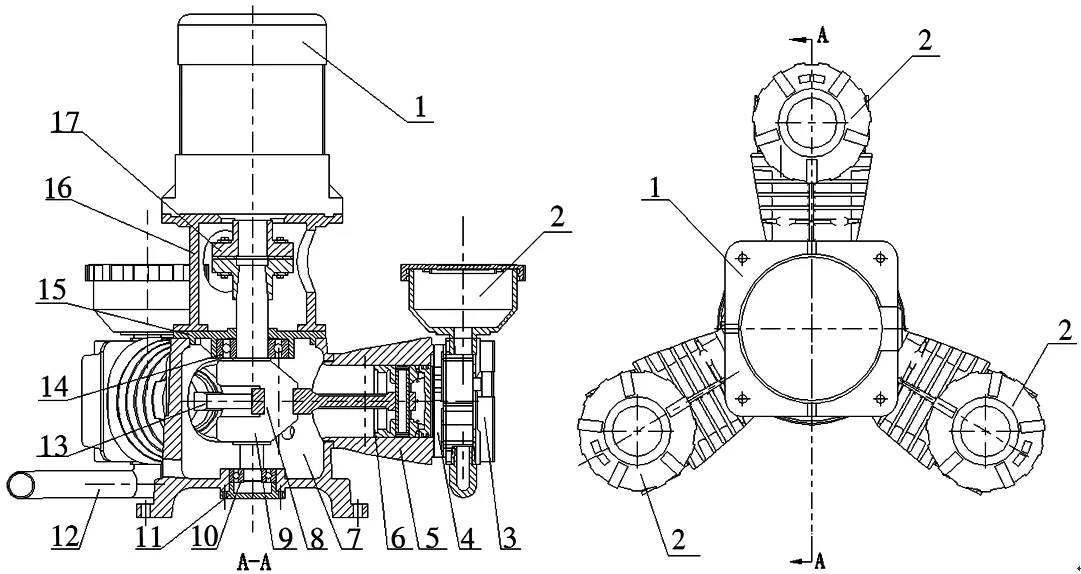
(a)A-A方向示意图 (b)整机俯视图
为解决三星型压缩机的曲轴最优配重问题,将曲轴的配重块质心到转轴中心的距离保持不变,配重质量作为设计变量,曲轴轴颈中心响应振幅作为目标函数,建立三星型压缩机的曲轴最优配重问题优化设计数学模型,利用ADAMS动力学仿真软件中的优化设计模块建立三星型压缩机的曲轴最优配重问题ADAMS动力学优化设计模型并求解,得到曲轴最优配重.
1 优化设计数学模型
一般而言,一个曲轴配重最优化问题可归结为:在已经满足给定的约束条件(决定n维空间 En中的可行域 D)下,选取适当的变量 X作为设计变量进行计算,使目标函数f(X)取得最优解[5].其数学表达式为:
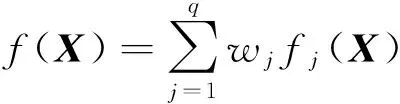
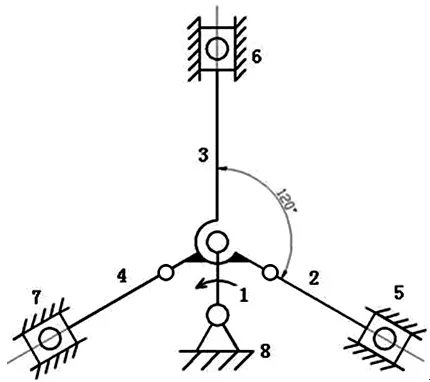
图2 三星型压缩机主传动系统的机构运动简图
对于三星型活塞式压缩机的曲轴配重优化问题,根据其主传动系统的机构运动方案,如图2所示,建立优化设计的数学模型如下:
(1)设计变量:因三星型压缩机的曲轴为双拐对称曲轴,故选取单个拐处的配重质量M作为设计变量,则总配重质量Z=2M.
(2)约束条件:①曲轴的配重块质心到转轴中心的距离e(偏心距)保持不变;②曲轴的配重质量M采用绝对变化范围的方法来定义.取值范围设定为0.4~1.5 kg.
(3)目标函数:将2个主轴承轴颈中心径向振动响应振幅的加权求和的最小值作为目标函数,即:
min(f(X))=min[λA1+(1-λ)A2]
(1)
上式中,A1、A2分别为两主轴承处的曲轴轴颈中心径向振动响应振幅,λ为加权因子,λ=0.5.目标函数与设计变量之间的关系隐含在描述三星型压缩机主传动系统动力学关系的微分方程之中,目前获取其解析表达式仍然很难.
2 ADAMS优化模型
根据三星型主传动系统的零部件几何图形及机构运动简图,利用UGNX软件建立所需零件的三维模型并进行装配,同时将装配模型导入ADAMS中.优化模型的建立还需按材质要求定义各零部件的材料密度到模型中,以及添加转动副、移动副、固定副等相关约束.在载荷的添加过程中,活塞力的添加是通过样条函数拟合后作用在活塞顶部来实现的,同时采用施加轴承反力的方式来替代曲轴处安放的轴承[7].因三星型压缩机的曲轴为双拐对称曲轴,故在曲轴双拐处各自添加一个参数化的配重质量球,使曲轴配重球的质心到转轴中心的距离e保持不变,并采用绝对变化范围的方法来定义设计变量的范围.这样就建立了三星型活塞式压缩机的主传动系统参数优化设计模型,如图3所示.
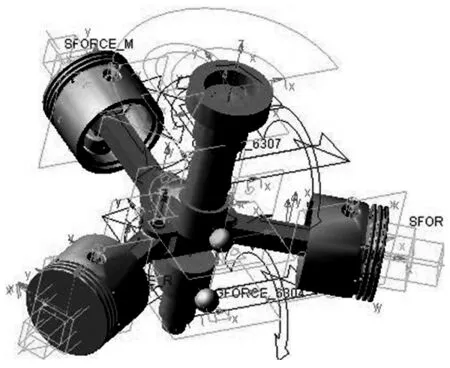
图3 三星型压缩机主传动系统参数优化模型
3 优化过程及计算结果
解决三星型压缩机曲轴配重的优化问题是利用软件ADAMS/View中优化设计模块功能,在满足所有约束条件后,并且设计变量在指定变化范围内,通过自动选择X的数值,由分析程序进一步求取所设定的目标函数的最大值或最小值.在此过程中ADAMS/View可进行多次仿真的自动运行,每次仿真改变虚拟样机模型的一个或多个设计变量,找到曲轴配重的最优设计方案.利用ADAMS软件进行优化设计的流程图如图4所示[8].
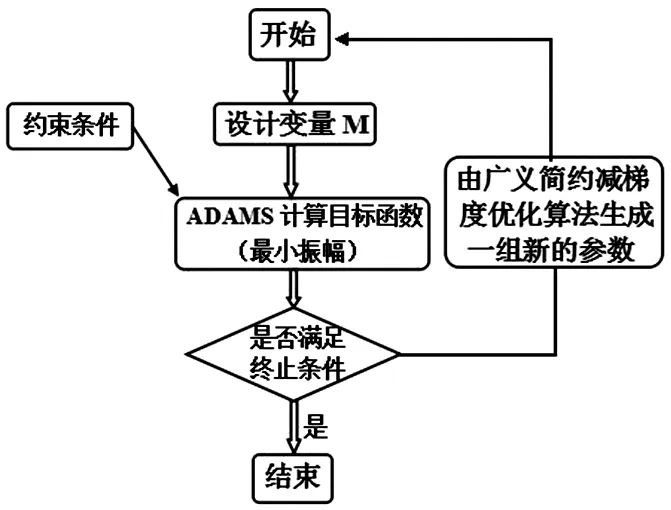
图4 ADAMS仿真优化流程图
在优化过程中以曲轴配重的质量作为设计变量,从而采用ADAMS提供的广义简约减梯度算法(OPTDES-URU)进行优化计算.目标函数与设计变量之间的关系曲线如图5所示.由图5可知有最优解,最小目标值为0. 023 5 mm,对应的配重质量M=1.0 kg,对应的偏心距e= 31 mm.由于三星型压缩机的曲轴为双拐对称曲轴,故曲轴的配重总质量Z=2.0 kg.
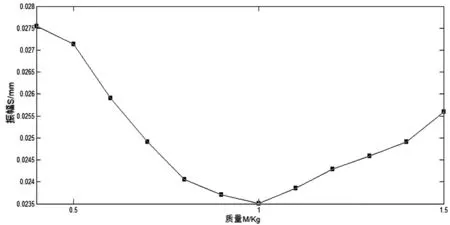
图5 目标函数与设计变量的关系曲线图
4 最优解仿真结果
通过ADAMS软件进行动力学仿真并求解,可得三星型压缩机的曲轴配重总质量Z为2.0 kg时的主传动系统动力学行为如图6~8所示.曲轴轴颈中心振动响应位移振幅和主轴承轴承反力峰值如表1所示.


图6 主轴承1、2的轴心径向位移响应

图7 主轴承1、2的径向轴承反力


图8 主轴承1、2的轴心轨迹
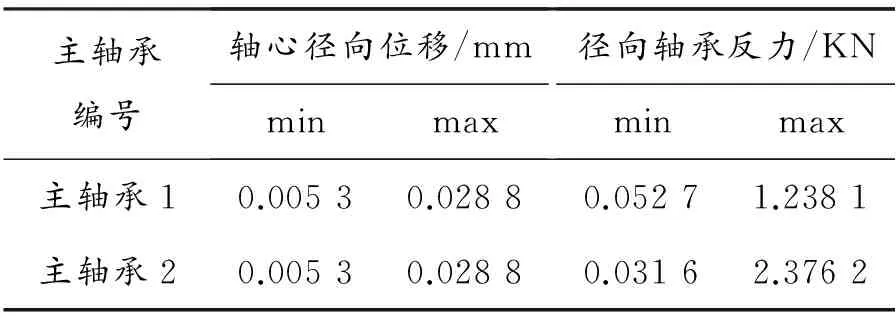
主轴承编号轴心径向位移/mmminmax径向轴承反力/KNminmax主轴承10.00530.02880.05271.2381主轴承20.00530.02880.03162.3762
由以上仿真结果可以看出:两个主轴承轴颈中心的运动轨迹完全一致且呈较为规则的三叶玫瑰线.轴心径向振动响应振幅相同,均为0.023 5 mm,但两主轴承反力峰值有所区别.其中,主轴承2反力峰值明显高于主轴承1,这是由于主轴承2的公称直径比主轴承1的公称直径大而引起的.
ADAMS优化仿真结果表明,优化后最优点(S=0.023 5 mm,M=1.0 kg,e=31 mm)的目标值比原设计点的目标值降低了17. 02﹪,使三星型压缩机的动力学性能更优.
5 结论
(1)曲轴配重的大小对此三星型压缩机的动力学性能有十分显著的影响,曲轴添加配重对改善其动力学性能十分必要.
(2)通过ADAMS优化后的最优点(S=0.023 5 mm,M=1.0 kg,e=31 mm)的目标值比原设计点的目标值降低了17. 02﹪,使得三星型压缩机的动力学性能更优.
以上结论可以为此三星型活塞式压缩机的曲轴设计及整机结构设计提供理论依据.
[1]李震,汤长根.一种活塞式压缩机:中国,CN104776005A[P].2015-07-15.
[2]徐军.15T2NL半无油活塞式空气压缩机设计和开发[D].南京:南京理工大学,2010.
[3]谢慧萍,张瑛.W2.85型活塞式空气压缩机虚拟设计与运动仿真的实现[J].现代制造工程,2008(1):121-123.
[4]张晓君,张波.涡旋压缩机传动系统研究与优化[J].机械设计与制造,2012(4):149-152.
[5]何芝仙,李昂.V型压缩机曲轴-滚动轴承系统动力学分析与优化[J].机械设计,2012,29(11):31-35.
[6]何芝仙,谭在银.W型压缩机曲轴-滚动轴承系统动力学分析与优化设计[J].机械设计与制造,2013(9):113-116.
[7]许金元,李震,何芝仙.基于ADAMS的压缩机主传动系统动力学优化问题研究[J].安徽工程大学学报(自然科学版),2013,28(4):40-43.
[8]郑建荣.ADAMS虚拟样机技术入门与提高[M].北京:机械工业出版社,2002:40-43.
(责任编辑穆刚)
Study on the problem of crankshaft counterweight optimization of a triple star-type reciprocating compressor
TANG Changgen1,LI Zhen1,HE Zhixian2,HAN Yanlin1
(1.College of Mechanical and Automotive Engineering, Anhui Polytechnic University, Wuhu Anhui 241000,China; 2. Key Laboratory of Mechanics, Anhui Polytechnic University, Wuhu Anhui 241000, China)
The triple star-type compressor is a new type of reciprocating compressor with good dynamic performance, and its main drive system is essentially composed of the major-minor linkage. In this paper, in order to study the problem of crankshaft counterweight optimization of the compressor, the mathematical model for the crankshaft counterweight optimization is established. Its objective function is the minimum response amplitude of crankshaft journal center, and the design variable is crankshaft counterweight. The optimal solution is obtained by using the ADAMS dynamics simulation software “optimization design” module. Optimization results show that the size of the crankshaft counterweight has a significant influence on the dynamic performance. The optimum target value of is lower 17.02﹪ than that of the original design point. The triple star-type compressor crankshaft counterweight is necessary to improve the dynamic performance.
the major-minor linkage; optimization; ADAMS software; amplitude
2016-02-29
国家自然科学基金资助项目(51575001);芜湖市科技计划资助项目(2014cxy07);大学生创新训练计划资助项目(201310363032).
汤长根(1990—),男,安徽六安人,硕士研究生,主要从事现代机械设计理论与方法方面的研究.
TH132
A
1673-8004(2016)05-0045-04
