基于CFD的离心泵结构参数优化

马飞红，唐铃凤，徐彬雪，万　鹏

(安徽工程大学机械学院， 安徽　芜湖　241000)



基于CFD的离心泵结构参数优化

马飞红，唐铃凤，徐彬雪，万鹏

(安徽工程大学机械学院， 安徽芜湖241000)

为获得离心泵的最佳结构参数，根据给定的离心泵设计参数确定离心泵的结构形式和性能评价指标，计算离心泵各结构参数，利用CFD对离心泵进行流场数值模拟分析，设计了叶轮结构L16(45)正交实验表，选择叶轮进口安装角βb1、出口安装角βb2、包角φ、进口直径D1、出口直径D2为正交实验的5个因素，完成了正交实验并对实验结果进行极差分析，得到各结构参数对各优化方向评价指标影响排序及其影响情况，构造出效率最大、汽蚀余量最小条件下的目标函数及统一目标函数，并运用遗传算法对离心泵效率和汽蚀进行多目标优化，得到离心泵的最佳结构组合参数.

离心泵；CFD；正交实验；极差分析；遗传算法；最佳组合参数

离心泵是应用广泛的一种水泵，它的开发过程中各项因素相互制约，造成开发过程漫长且复杂.在工程实际中，离心泵叶轮的设计依旧采用半理论半经验的设计方法，设计出的模型性能通常不是最优的.因此，在传统设计的基础上对叶轮进行优化设计非常必要.

随着计算流体力学的发展，CFD技术越来越受到设计人员的青睐.赵斌等人在基于CFD技术的离心泵叶轮优化设计时，为了减少重新设计的成本，在不改变泵整体结构的前提下，以叶轮型线为设计变量来优化叶轮尺寸[1].谈明高等人针对离心泵出口角对能量性能的影响进行CFD研究，结果表明随着叶片出口角的改变，泵的效率存在极值点[2].段敏等人基于CFD的离心泵三维内流场分析运用CFD软件，采用标准湍流模型和SIMPLE算法对离心泵内流场进行分析，得到叶轮工作面和背面压力分布的不均匀性[3].上述研究仅针对个别关键因素进行分析研究，未针对离心泵的多个结构因素进行流场分析及结构优化研究，且未使用优化算法对泵的各参数进行优化.本文采用CFD软件对离心泵内流场进行模拟，并选取叶轮进口安装角βb1、出口安装角βb2、包角φ、进口直径D1、叶轮出口直径D2为正交实验的5个因素，完成了正交实验并对实验结果进行极差分析，得到各结构参数对各优化方向评价指标影响排序及最佳组合参数及其影响情况，构造出效率最大和汽蚀余量最小条件下的目标函数及统一目标函数，并以D1、D2、b1、b2、βb1、βb2、Z为设计变量加以约束条件对离心泵进行全性能优化，运用遗传算法对离心泵效率和汽蚀进行多目标优化，得到离心泵的最佳结构组合参数.

1　离心泵结构设计

离心泵的基本参数为：设计流量Q=25 m3/h，设计扬程H=80 m，额定转速n=2 900 rpm，叶轮进口直径D1=75 mm，D2=255 mm，叶轮进口宽度b1=20 mm，出口宽度b2=7 mm，进口安装角βb1=25°，出口安装角βb2=30°，包角φ=110°.根据上述参数，建立叶轮、蜗壳流道物理模型并装配，如图1所示.

图1　流体域模型

2　CFD流场模拟

2.1网格划分

网格划分是流动控制方程数值离散的基础，网格质量的好坏直接影响到解析的敛散性和结果的准确性.叶轮区网格数127 794，蜗壳区727 398，进口段网格数2 408，网格总数 854 692，如图2所示.

图2　网格划分

2.2控制方程

离心泵内部流动属于三维、黏性、非定常湍流流动，其运动规律符合 Naiver -Stokes 方程.

连续方程：

(1)

动量方程：

(2)

不可压N-S方程：

(3)

k-ε方程：

(4)

(5)

(6)

上式中，ρ是流体密度，p*是包括离心力的压强，湍动能为k，ω是角速度，εijk是张量，μ是有效黏度系数，U为速度矢量，p是压力，t是时间，ϑ为流体运动黏性系数. i、j分别取1、2、3，σk=1.0，σε=1.3，Cμ=0.09，C1=1.44，C2=1.92.

2.3边界条件设定

对边界条件设置有: 流体介质的基本属性，包括流体介质的密度、温度、黏度大小、介质的含气量、蒸汽密度、饱和蒸汽压等，参数如表1所示.除此之外还要对叶轮叶片进行转子设置，对流体介质的入口、出口进行设置以及旋转面设置.

将压力设为进口条件，将入口段进口处设为标准大气压.采用流量出口边界条件，设置出口流量为额定工况流量，即Q=0.006 944 m3/s.将叶片设定为旋转部件，转速为2 900 rpm.将所有同叶轮一起旋转的壁面(即叶轮的工作面和背面)均设置为旋转壁面，转速大小与叶轮叶片一致，且移动方向和速度要与叶轮保持一致.其余面可直接默认成静止面.

2.4流场模拟

完成边界条件设置后，设定计算迭代步数便进行求解计算，得到设计工况下离心泵叶轮内部流场的残差动态监测过程.本文设定的计算迭代步数为1 000步.图3为残差曲线图.从图3中可以看出，迭代步数在达到500次左右时曲线已收敛.

图3　残差曲线图

图4为离心泵压力分布图.从图4中可以看出，从叶轮进口处到叶轮出口处压力数值是逐渐增加的，且靠近蜗壳出水口的压力明显大于叶轮中的其他区域，说明在叶轮旋转过程中相对于蜗壳的不同位置，从叶轮到蜗壳液体流动不均匀，且蜗壳反作用于叶轮，使得叶轮中两叶片之间可能出现涡流.

图4　压力云图

图5为离心泵速度分布图.从图5中可以看出，从叶轮进口处到叶轮出口处，速度的数值是逐渐增加的.由于叶片的作用使得靠近叶片处的流动效果比远离叶片中心的流动效果要好，且相对远离叶片的中间位置出现漩涡，严重影响叶轮区域液体的正常流动.

图5　速度云图

由图6可以看出，离心泵叶轮范围内出现明显低压区，且在靠近蜗壳的叶轮边缘的叶片背面出现负压区.

图6　总压分布图

由图7中可以看出，由于叶轮进口处压力很低，达到介质在常温下汽化的临界压力，故而叶轮进口处发生汽蚀，气体体积分数高达0.848 36.这与实际情况相符.

图7　气体体积分数图

3　正交实验与极差分析

3.1正交实验

离心泵的结构往往需要考察的实验因素较多，进行全面实验，模拟实验规模大，实验较为麻烦，且有可能因为实验条件和实验周期的限制而难以实施.

正交实验是在试验因素的全部水平值中寻找出部分有代表水平的组合进行实验.通过较少次数实验及对这些实验结果的分析，得到全面的实验情况，寻找到最优因素水平组合.综合考虑离心泵的效率和汽蚀，选取叶轮进口直径、出口直径、叶轮进口角、出口角和包角5个结构尺寸作为实验因素.每个因素设置4种水平，取值如表2所示.

在离心泵结构正交实验中，不考虑各实验因素间的交互作用，对于五因素四水平的正交实验可以选用的正交表为L16(45).离心泵正交实验的因素水平表如表2所示.

表2　叶轮正交实验因素水平表

3.2极差分析

3.2.1各因素对效率的影响趋势分析

根据表3计算各因素各水平下效率平均值的极差.从表4中可以明显地看出各因素对效率的影响由大到小依次为：叶轮出口直径D2、包角φ、进口直径D1、进口角βb1、出口角βb2.为了更直观地观察变化趋势，绘制了各因素对效率的影响趋势图如图8所示.根据评价指标，得到最优水平组合为：A2B4C4D1E2，即当叶轮进口直径D1为74 mm、出口直径D2为258 mm、进口角βb1为30°、出口角βb2为20°、包角φ为105°时损失最小，表明此参数下的离心泵具有最大效率.该优化得到的离心泵结构参数不在已有的实验中，用CFD软件进行实验验证，得到该组数据的最大效率为56.80﹪，与已有的16组实验数据对比发现该实验效率接近正交实验中的最大值.

考虑效率条件下的最佳组合参数：A2B4C4D1E2.最优水平组合为：A2B4C4D1E2，即当叶轮进口直径D1为74 mm、叶轮出口直径D2为258 mm、进口角βb1为30°、出口角βb2为20°、包角φ为105°时，可获得最大效率，表明此参数下的离心泵具有最大效率.

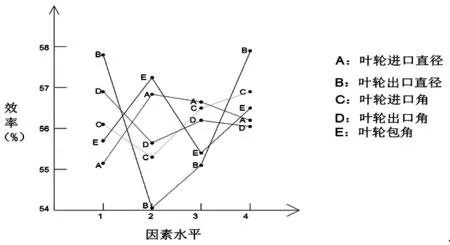
图8　各参数对效率的影响趋势

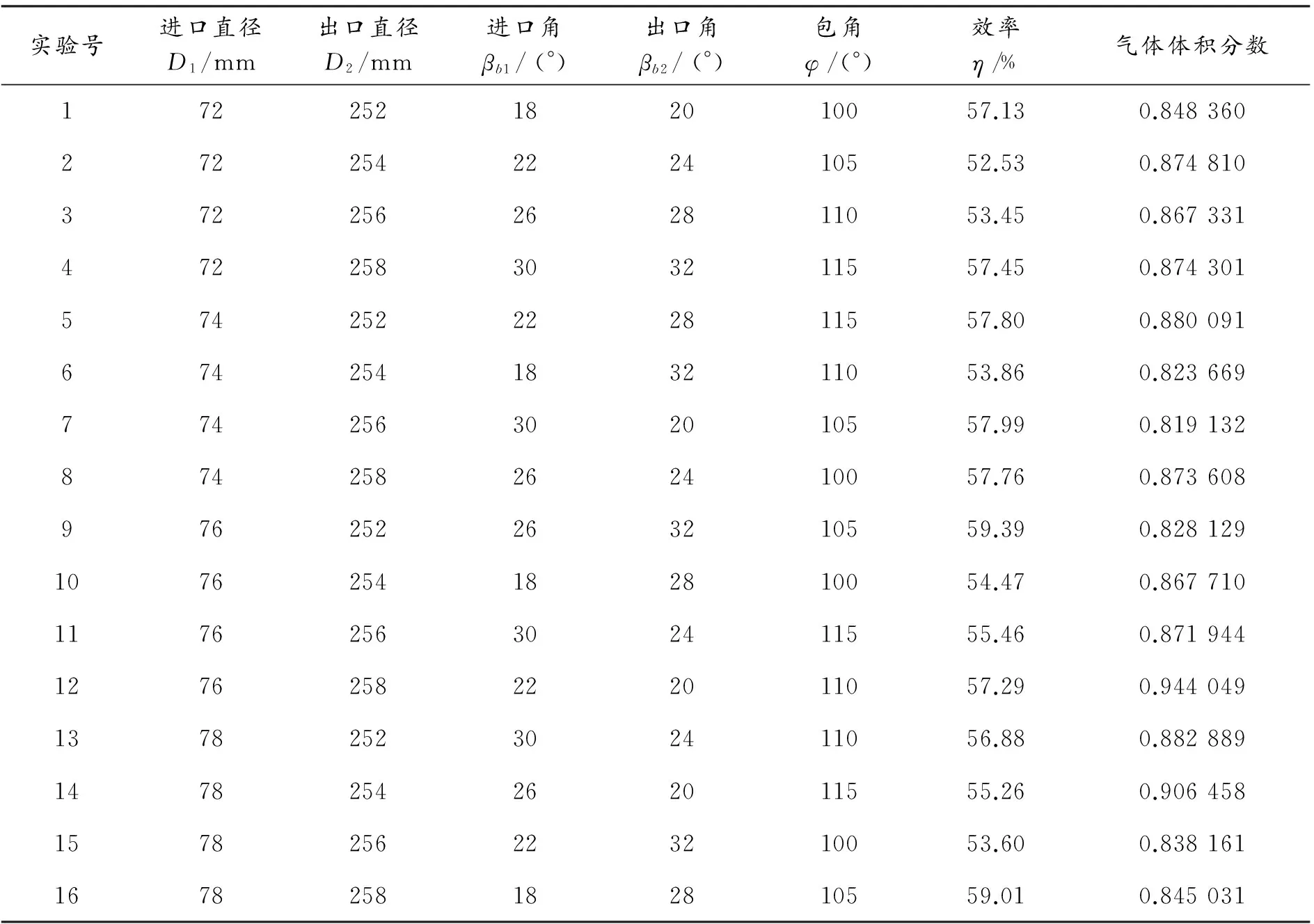
实验号进口直径D1/mm出口直径D2/mm进口角βb1/(°)出口角βb2/(°)包角φ/(°)效率η/﹪气体体积分数172252182010057.130.848360272254222410552.530.874810372256262811053.450.867331472258303211557.450.874301574252222811557.800.880091674254183211053.860.823669774256302010557.990.819132874258262410057.760.873608976252263210559.390.8281291076254182810054.470.8677101176256302411555.460.8719441276258222011057.290.9440491378252302411056.880.8828891478254262011555.260.9064581578256223210053.600.8381611678258182810559.010.845031

表4　各因素对效率的影响

续表4

3.2.2各因素对汽蚀的影响趋势分析

根据表3计算各因素各水平下气体体积分数平均值的极差.从表5中可以明显地看出各因素对汽蚀的影响由大到小依次为：进口角βb1、包角φ、叶轮出口直径D2、出口角βb2、进口直径D1.为了更直观地观察变化趋势，绘制了各因素对气体体积分数的影响趋势图如图9所示.根据评价指标，得到最优水平组合为A2B2C1D3E1，即当叶轮进口直径D1为74 mm、叶轮出口直径D2为254 mm、进口角βb1为18°、出口角βb2为28°、包角φ为100°时，可获得最小气体体积分数，表明此参数下的离心泵的汽蚀有较好的改善.该优化得到的离心泵结构参数不在已有的实验中.用CFD软件进行实验验证，得到该组数据的最小气体体积分数为0.843 46，与已有的16组实验数据对比发现该实验气体体积分数接近正交实验中的最小值.

图9　各参数对气体体积分数的影响趋势

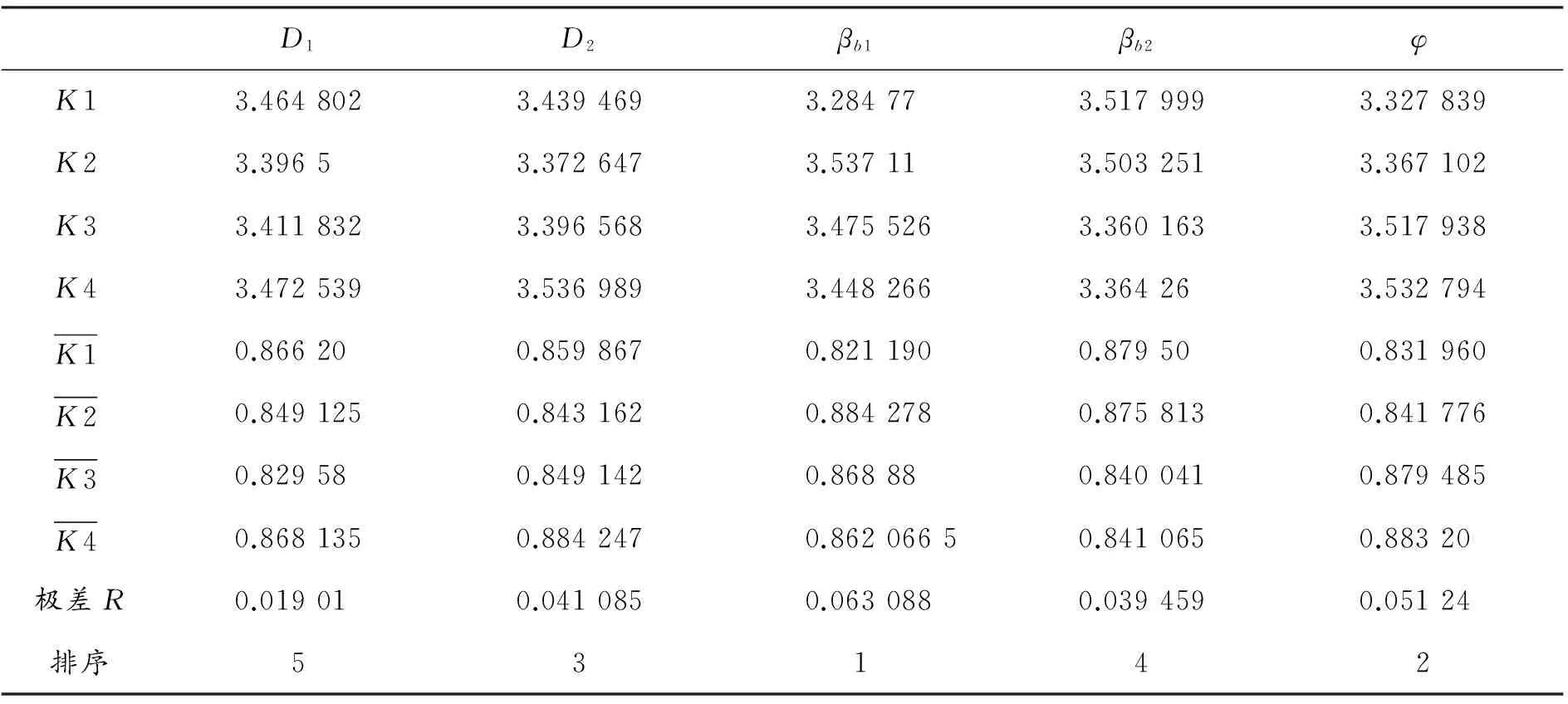
D1D2βb1βb2φK13.4648023.4394693.284773.5179993.327839K23.39653.3726473.537113.5032513.367102K33.4118323.3965683.4755263.3601633.517938K43.4725393.5369893.4482663.364263.532794K10.866200.8598670.8211900.879500.831960K20.8491250.8431620.8842780.8758130.841776K30.829580.8491420.868880.8400410.879485K40.8681350.8842470.86206650.8410650.88320极差R0.019010.0410850.0630880.0394590.05124排序53142

考虑汽蚀条件下的最佳组合参数A2B2C1D3E1.最优水平组合为A2B2C1D3E1，即当叶轮进口直径D1为74 mm、叶轮出口直径D2为254 mm、进口角βb1为18°、出口角βb2为28°、包角φ为100°时，可获得最小气体体积分数，表明此参数下的离心泵的汽蚀有了较好的改善.

4　遗传算法优化

4.1离心泵效率最大目标函数

根据Stodola公式,当入口无预旋时，泵的理论扬程为：

(7)

η=ηmηυηh

(8)

机械效率可表示为：

(9)

上式中的Pm是离心泵的机械损失，P是轴功率，且

容积效率可表示为：

(10)

(10)式中，ns为比转数.可以看出，ηυ仅与n、Q和H有关，而这几个参数都是不变量，因此可以推出ηυ是常量(用A表示).因此，总效率可表示为：

η=Aηmηh

(11)

水力效率可表示为:

(12)

其中，S为离心泵的水力损失.

将(9)、(12)式代入(11)式中可以得到离心泵总效率的表达式为：

(13)

由(13)式可以得出效率最大目标函数为:

(14)

4.2离心泵最小汽蚀余量目标函数

离心泵汽蚀余量基本方程为:

(15)

假定进口无预旋，则：

(16)

上式中，k1=0.876，k2=0.91，均为常数.

将(16)式代入(15)式可以得到：

(17)

汽蚀余量最小目标函数为：

min[f2(x)=NSPHr]

(18)

4.3目标函数处理

4.3.1统一目标函数

本文采用权重系数变换法处理多目标函数.对一个多目标优化函数，假设每个子目标函数fi(x)(i=1,2,…,n)赋予权重ωi，则各目标函数加权可表示为：

(19)

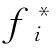
4.3.2分目标权重系数的确定

构造互补矩阵B(k)(k=1,2,…,n)的第一列列向量B1(k)=(b11(k),b21(k),…,bn1(k)).其中，n为矩阵的阶数，b11(k)按(20)式计算：

b11(k)=(bk1)-1bk1,

b21(k) =(bk2)-1bk2,

……

bn1(k) =(bkn)-1bkn

(20)

构造超传递近似矩阵的第1列列向量

其中

(21)

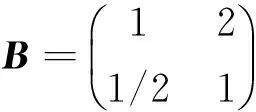
构造互补矩阵B(k)(k=1,2)第1列列向量为：

通过归一化处理后，可得权重系数为：ω=(0.667,0.333).即ω1=0.667，ω2=0.333.

4.3.3约束条件

根据离心泵的水力模型对设计变量的取值范围进行适当调整，可以得到其约束条件为：

(22)

4.4遗传算法优化

本文采用遗传算法工具箱GA进行目标优化，设置种群数为1 000，交叉概率0.7，变异概率0.01，以目标值相对误差为收敛准则.相对误差可表示为：

(23)

在MATLAB中进行GA程序，得到如图10所示的迭代图.优化结果如表6所示.

运用优化后的各参数重新建模，且对所建模型进行CFD分析.通过对优化的模型进行CFD

分析，可以通过泵的进出口压差(如图11所示)计算离心泵的效率为59.815 4﹪，与之前的56.80﹪相比提高了3.015 4﹪.从图12中可以看出，优化后的模型在进行CFD分析后气体体积分数为0.802 245，与之前的0.843 46相比减小了0.041 215，离心泵的整体性能有所提高.

图10　迭代收敛图

图11　优化后的压力云图

图12　优化后的气体体积分数

D1b1D2b2β1β2Z优化前7520255725306优化后78242506.820266

5　结论

(1)本文设计了L16(45)正交实验表.各因素对离心泵效率的影响从大到小顺序依次是：叶轮出口直径D2、包角φ、进口直径D1、进口角βb1、出口角βb2.效率条件下的最佳组合参数为：A2B4C4D1E2.各因素对离心泵汽蚀的影响从大到小顺序依次是：进口角βb1、包角φ、叶轮出口直径D2、出口角βb2、进口直径D1.汽蚀条件下的最佳组合参数为：A2B2C1D3E1.

(2)运用遗传算法对以效率最大和汽蚀余量最小为优化目标进行多目标优化，优化得到离心泵的最佳组合参数为：D1=78mm、D2=250mm、b1=24mm、b2=6.8mm、βb1=20°、βb2=26°、Z=6.

(3)通过对优化后的模型进行CFD分析，可以发现效率由之前的56.80﹪增加到59.815 4﹪，提高了3.0154﹪；气体体积分数由之前的0.843 46减小到0.802 245，降低了0.041 215.可以看出，离心泵的整体性能有所提高.

[1]赵斌，孙铁，周长茂，等. 基于CFD技术的离心泵叶轮的优化设计[J].石油化工设备技术，2007, 28(6): 43-45.

[2]谈明高，刘厚林，袁寿其，等. 离心泵出口角对能量性能影响的CFD研究[J].中国农村水利水电，2008，(11):104-106.

[3]段敏，于海洋，葛鑫. 基于CFD的离心泵三维内流场分析[J].辽宁工业大学学报，2015，35(6): 392-395.

[4]李凯，唐铃凤，辛厚智. 脱硫除尘用风机流场模拟及其结构优化研究[J].重庆文理学院学报，2016(2)：109-115.

[5]冯喆. 离心泵叶轮内部流场模拟及其结构改进设计[J].机械设计与制造，2015, 5(5): 16-20.

[6]范恒艮，王幼民，唐铃凤. 离心泵内部流场的三维数值模拟及流动分析[J].机械工程师，2007(1): 49-51.

[7]张人会，杨军虎，李仁年.离心泵叶轮的参数化设计[J].排灌机械工程学报，2009, 27(5): 310-313.

[8]LIY,DONGWL,HEZH.Flowinstabilityofacentrifugalpumpdeterminedusingtheenergygradientmethod[J].JournalofThermalScience, 2015, 24(1): 44-48.

[9]BACHAROUDISEC,FILIOSAE,MENTZOSMD,etal.Parametricstudyofacentrifugalpumpimpellerbyvaryingtheoutletbladeangle[J].OpenMechanicalEngineeringJournal, 2008, 2(5): 75-83.

[10]李敏强，寇纪淞，林丹．遗传算法的基本理论与应用[M]. 北京：科学出版社，2002．

(责任编辑穆刚)

Optimization of structure parameters of centrifugal pump based on CFD

MA Feihong,TANG Lingfeng,XU Binxue,WAN Peng

(College of Mechanical and Automotive Engineering, Anhui Polytechnic University,Wuhu Anhui 241000, China)

In order to obtain the optimum structure parameters of the centrifugal pump, based on the design parameters of a given centrifugal pump, the structural form and performance evaluating index of centrifugal pump were determined and the structural parameters of the centrifugal pump were calculated. Using CFD to make flow numerical simulation analysis on centrifugal pump, theL16(45) orthogonal test table of Impeller structure was designed, selecting of impeller inlet angle, outlet angle, wrap angle, inlet diameter, outlet diameter as the five factors of orthogonal experiment,and the orthogonal experiment was completed and the range analysis of the results was made, and the influence of structure parameters were obtainedon the ranking optimization direction of evaluation index and the influence. The object function and unified objective function with the maximum efficiency and minimum cavitation were constructed, using genetic algorithm to optimize the efficiency and cavitation of centrifugal pump, and the best structure parameters of the centrifugal pump were obtained.

centrifugal pump; CFD; orthogonal experiment; range analysis; genetic algorithm; optimal combination parameter

2016-03-12

马飞红(1990—)，女，回族，安徽阜阳人，硕士研究生，主要从事机械制造及其自动化方面的研究.

TH11

A

1673-8004(2016)05-0049-08