改进GM（1，1）模型在建筑工程现金流预测中的应用

于津苹，汪 茵，高 平

（1. 东北财经大学 投资工程管理学院，辽宁 大连 116025 Email:lnuyujinping@163.com；2. 杭州市水务控股集团有限公司，浙江 杭州 310000）

改进GM（1，1）模型在建筑工程现金流预测中的应用

于津苹1，汪 茵2，高 平1

（1. 东北财经大学 投资工程管理学院，辽宁 大连 116025 Email:lnuyujinping@163.com；2. 杭州市水务控股集团有限公司，浙江 杭州 310000）

准确的建筑工程现金流预测是提高建筑行业投资和融资决策效果、获得稳定收益的前提，合理的现金流预测方法是确保预测结果准确的关键。引入灰色预测和“1/4：1/3”现金流预测理论，提出基于权重因子的背景值构造，并以实地收集的10余个建筑工程项目为样本，采用黄金分割法和对半分割法对GM（1，1）模型进行改进，以提高GM（1，1）模型在建筑工程现金流预测实践中的适用性和适应性。实证结果表明，改进后的灰色预测模型能够以较高精度预测建筑工程现金流，从而为公司投资、融资决策以及资金管理提供可靠依据。

GM（1，1）模型；建筑工程；现金流预测

建筑工程项目作为非可逆的动态一次性工作，需要大量的现金流。在项目实施过程中对临近周期内现金流的准确预测及把握，是项目顺利进行的必要条件，是企业资金管理能力和效果的直观反映，也是企业进行投资、融资决策的基础。这里的现金流指建筑工程项目实施过程中的现金流支出，故采用合适的方法对施工过程中的现金流进行合理的预测是建筑企业关注的焦点，由此也引发国内外学者对此问题的探究。

国外对建筑工程现金流预测的研究比较活跃。从早期的简单“1/4:1/3”模型［1］，到后来的以工期或完工百分比为自变量、以工程现金流为因变量的一元预测方程［2～4］，再到现在的以先进数学理论及方法为工具建立的复杂现金流预测模型［5～8］，各研究说明现金流的预测方式多样、方法繁多，而不同方法又因环境不同存在着一定局限性。国内的研究则较为匮乏，王伟红等［9］提出基于移动权重法的建筑项目建设现金流预测模型；王梅［10］采用物元分析法估算房地产项目的现金流，但都是从企业角度而非建筑工程项目本身来研究现金流预测。刘文杰［11］分别从房地产开发项目的策划期、计划期和建设期3个阶段阐述了提高项目现金流预测水平的方法；彭露［12］从房地产全过程规划角度提出了提高资金使用效率、降低资金链断裂风险的项目现金流规划体系。

本文在国内外研究的基础上，针对建筑工程的特点，以“1/4:1/3”模型为理论基础，引入灰色预测理论预测建筑工程现金流，建立一种基于权重因子背景值的灰色预测改进模型。可在原始数据较少情况下进行，实现了研究方法和数学工具上的创新，为国内建筑工程现金流预测提供了一种可靠的方法。

1　建筑工程现金流预测的价值

（1）建筑工程现金流的准确预测能够提高企业投资决策的合理性。根据帕累托原理，工程项目前期影响远大于后期，前期投资决策在整个项目实施过程中至关重要。项目前期投资决策一旦出现失误，就会造成资源的浪费，增加资金机会成本，并对整个建筑工程项目的效益产生重大影响。对建筑工程现金流预测模型的研究，可以有效地指导建筑工程投资者作出合理的决策，对投资方最大限度地获取收益具有重要的现实意义。

（2）实现建筑工程现金流的预测可以提高融资决策的准确性。预测是决策的先导，是实现科学管理的重要环节。预测的结果越精确，决策的合理性就越高。作为建筑工程项目的资金支付方，对现金流预测精度越高，所制定的融资计划就越合理。而作为建筑工程项目的实施方，对现金流预测精度越高，对项目资金的运用和控制能力也越强。

（3）对建筑工程现金流进行有效预测，可提高项目实施过程资金管理的有效性。建筑工程现金流预测不仅可以提高项目前期融资、投资的合理性和准确性，在提高项目实施过程资金管理有效性方面也发挥着重要作用。项目实施过程中，无论是投资方还是施工方都可以将前期现金流预测结果作为比较基准，设定可接受偏差率并以此监视实际工程现金流的发生是否合理，一旦发生重大偏差，则立即寻找造成偏差的原因并采取必要的纠偏措施，以提高项目实施过程资金管理的有效性。

2　“1/4:1/3”现金流预测与灰色预测分析

2.1“1/4:1/3”现金流预测

“1/4:1/3”现金流预测模型由Gates等提出［13］，是早期的现金流预测模型。“1/4:1/3”模型是指在建筑工程实施过程中，1/4的现金流支出发生在施工进度的前1/3阶段，1/2的现金流支出发生在施工进度的中间1/3阶段，剩余1/4的现金流支出发生在施工进度的剩余1/3阶段。以建筑工程成本为1000万元、工期为 12个月的项目为例，施工进度前 4个月内现金流支出额共计250万元，每个月62.5万元；施工进度中间4个月内现金流支出额共计500万元，每个月125万元；施工进度最后4个月内现金流支出额共计250万元，每个月62.5万元。

本文以“1/4:1/3”现金流预测模型作为研究基础，结合建筑工程现金流的特点，将建筑工程实施过程划分为3个阶段，并将此作为灰色预测模型的背景值序列构造的前提。

2.2灰色预测基本原理

灰色预测是通过原始数据的处理和灰色模型的建立，研究系统内部的发展规律，揭示系统内各因素间的联系，并对系统的未来状态及变化发展趋势做出科学的定量预测。其数学建模思路是通过对呈离散状态的原始数据序列进行处理，通过关联分析提取建模所需的变量，建立灰色模型（Grey Model，GM），并用于实际预测。

本文采用的是灰色模型中应用最为广泛的一次累加模型即GM（1，1）模型，该模型是由包含一个单变量的一阶微分方程构成的灰色数列预测模型，其原理是将随机、波动、离散的原始数据序列进行一次累加弱化其随机性，生成指数规律性较强的灰色序列后再进行灰色建模，并将模型运算得出的数据进行一次累减，得到原始数据序列的对应预测值，然后进行预测。

2.3灰色预测适用性分析

合理有效的建筑工程现金流预测能够为企业投资、融资提供可靠的数据支持，提高企业决策能力。在建设工程实际施工中，现金流预测的特点:一是随着项目的不断推进，现金流累计值随着时间的变化呈S形，表现为不断上升且上升趋势明显；二是建筑工程现金流预测是基于已完工程现金流数据，鉴于建筑工程特点，所能参考的基准数据有限，难以获取大量数据。而与建筑工程现金流特点

表1　灰色预测与其他预测方法的对比

灰色预测以小样本、少数据建模为任务，适用于上升趋势明显但又很难获取大量数据的时间序列的预测。在样本数量方面，数据量要求较少，计算复杂性低；在预测精度方面，中短期预测中能达到一般模型难以实现的拟合精度。虽然不同参数类型的灰色模型依据不同情况需要的数据量有所差异，但在极端情况下，灰色预测最少可以只有4个数据进行预测［14］，其预测过程见图1。灰色预测的特点与建筑工程现金流的特点相契合，为应用灰色模型预测建筑工程现金流提供基础性条件。

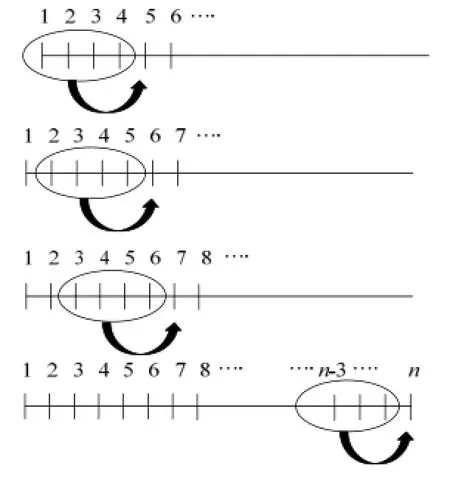
图1　灰色预测示意图

2.4GM（1，1）模型改进

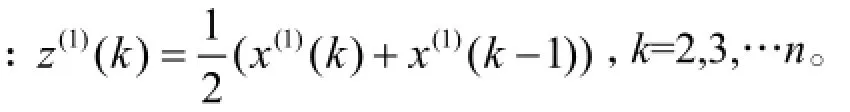
本文基于“1/4:1/3”现金流预测理论［11］，遵循残差最小化原则，分别采用黄金分割法和对半分割法，利用迭代优化算法搜索权重因子α的最优值，对3个阶段分别建立背景值序列，以提高GM（1，1）模型在建筑工程现金流预测实践中的适用性和适应性。具体步骤如图2所示。

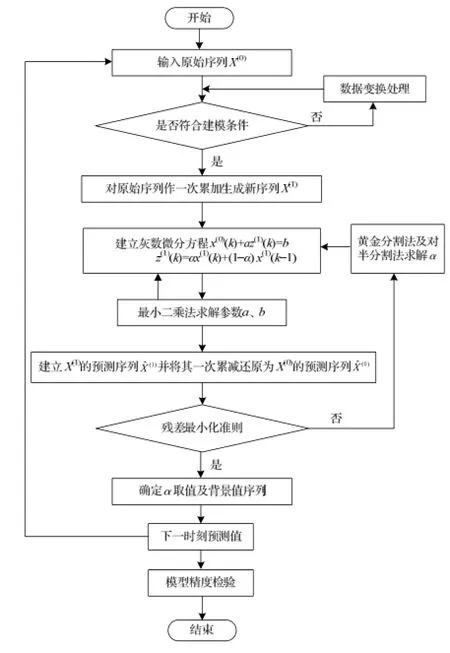
图2　基于权重因子背景值改进的GM（1，1）模型流程图

3　改进GM（1，1）模型对建筑工程现金流的预测

3.1原始数据的收集与处理

通过样本数据收集，选取了我国南北区域近几年 12个具有典型代表意义的房屋建筑工程，分别位于吉林、沈阳、大连、天津、惠州、贵阳等城市。其中住宅类项目8个，公共建筑类项目2个，商业建筑类项目2个，其建筑规模、合同总价款及总工期如表2所示。

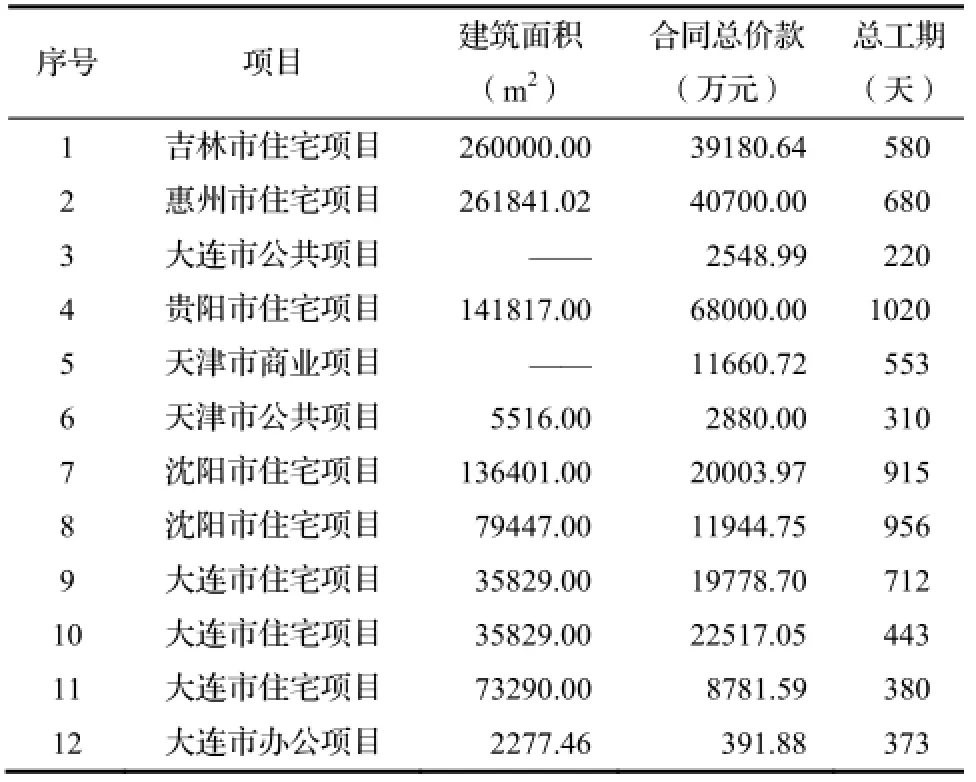
表2　案例建筑规模、合同总价款及总工期汇总表

考虑上述案例现金流数值较大，采用数据归一化方法，以月为时间序列单位，将现金流数据映射到（0，1）范围内，即以现金流百分比（原始每月现金流/项目现金流总额）作为现金流序列值。根据灰色预测理论，现金流序列值数据归一化后的序列经检验满足准光滑条件，可以进行灰色建模。

3.2改进GM（1，1）模型的建立

根据预处理后的原始序列，建立建筑工程现金流改进GM（1，1）模型Ⅰ和改进GM（1，1）模型Ⅱ，具体步骤如下。

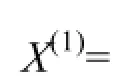
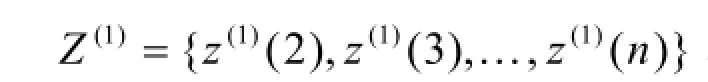
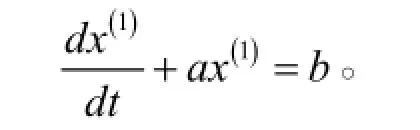
第五步:采用黄金分割法和对半分割法搜索α最优值:

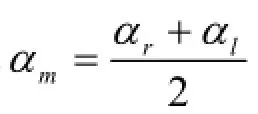
黄金分割法:再设存在α1和α2，令:

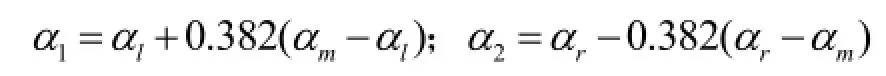
对半分割法:再设存在α1和α2，令:

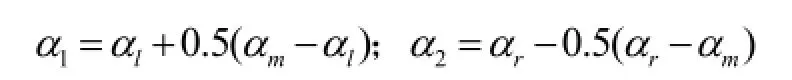
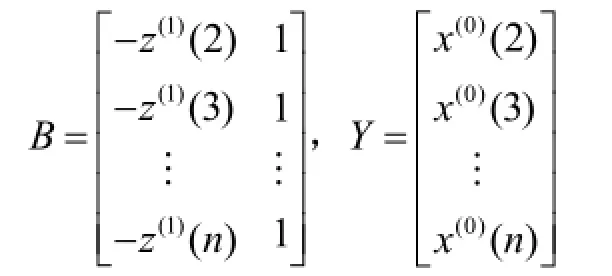
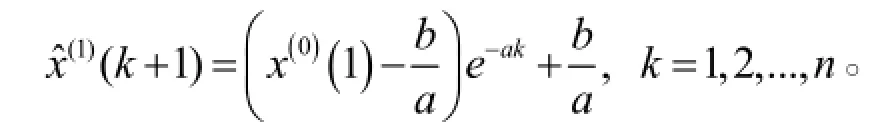
并将（1）ˆX还原即可得到 X（0）的预测序列0ˆX（），即:

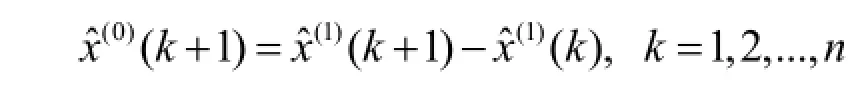
重复第五步到第八步，直至反复迭代100次后，得到权重因子α最优值。

第九步:依上述步骤，按照“1/4:1/3”现金流预测理论将每个案例的施工过程划分为3个阶段，分别搜索每个案例3个阶段的α值，即α1、α2、α3。

第十步:计算12个案例每个阶段α的平均值，设为α实证，即:

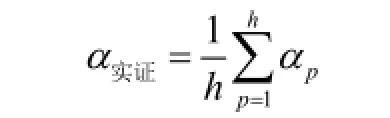
式中，p为案例序号1～12，αp为每个案例每个阶段的α值。

3.3构造新的背景值序列

根据上述步骤，经过Matlab编程并运行程序，通过对权重因子α最优值的搜索，得出黄金分割法和对半分割法下的12个案例每个阶段的α值水平，并据此求出α平均值。黄金分割法下3个阶段背景值构造的权重因子 α平均值分别为0.473990887、0.542807249、0.465694662；对半分割法下 3个阶段背景值构造权重因子α平均值分别为0.474696618、0.544126268、0.470637528。根据黄金分割法下搜索的权重因子α最优值构造的3个阶段的新的背景值序列分别为:

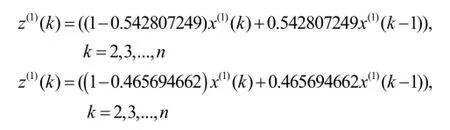
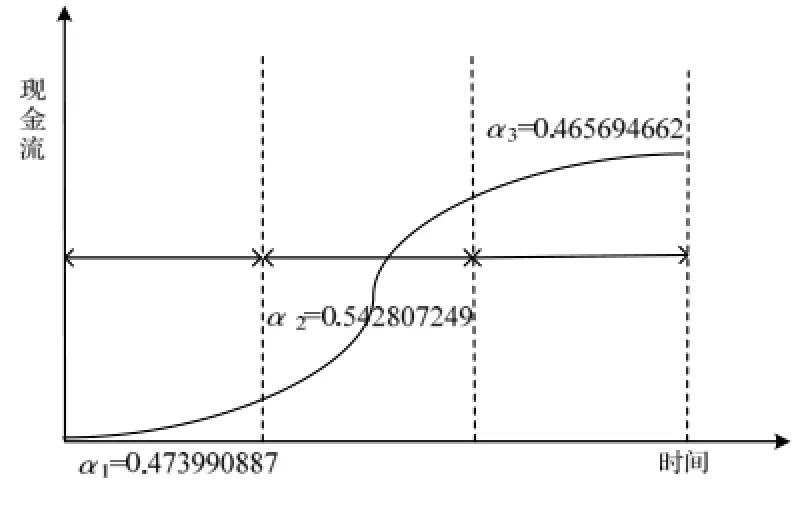
图3　黄金分割法下三个阶段背景值构造的权重因子α平均值

根据对半分割法下搜索的权重因子α最优值构造的3个阶段的新的背景值序列分别为:

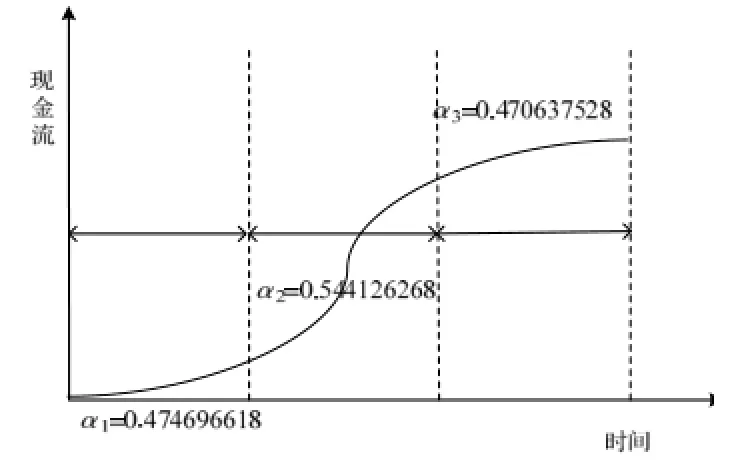
图4　对半分割法下三个阶段背景值构造权重因子α平均值

3.4改进模型残差检验

根据权重因子α最优值搜索程序，在得出α最优值的同时输出α值对应的误差值。一般情况下，当模型精度p＞90%时，则表明通过序列建立的近似微分方程达到了较好的精度要求［18］。经计算，本文采用黄金分割法与对半分割法下所建模型的精度分别为96.3389817%、94.3292386%，说明该预测达到了较高的精度要求。

3.5实际工程中的应用检验

为了验证上述改进GM（1，1）模型的精确性，选取两个实际建筑工程作为模型应用的检验实例，两个实例的合同总价款分别为 28395.21万元和38175万元。同样采取数据归一法进行处理。经检测，数据序列满足光滑条件，可以进行灰色预测建模。通过所建立的模型，进行数据录入，将所得结果与原始数据和传统GM（1，1）模型预测数据进行对比，如表3、表4所示，精度对比结果如表5所示。

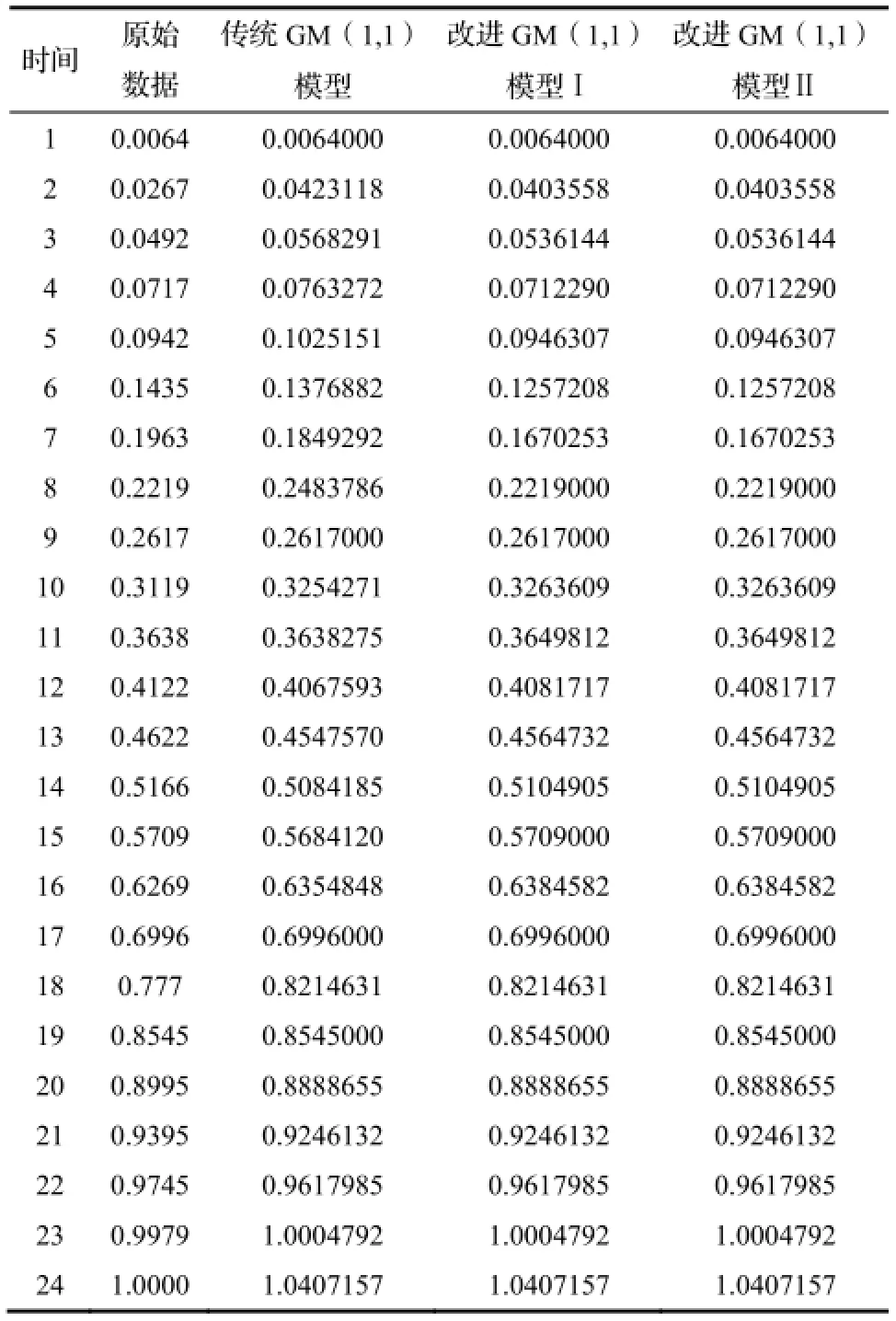
表3　实例1数据

由此可见，基于权重因子α的背景值构造对模型进行改进后，误差有所降低，预测精度有所提高，较传统GM（1，1）更具有预测优势，因此，改进后的GM（1，1）模型能够对建筑工程现金流进行高精度预测。

4　结语

建筑工程现金流预测对建筑企业至关重要，有效的现金流预测能够帮助企业提高项目实施工程中的运营效率。在实践应用中，预测方法决定预测结果准确度与精度，选取合适的预测方法进行建筑工程现金流预测是本文研究的重点。本文采用黄金分割法和对半分割法，基于权重因子对传统GM（1，1）模型的背景值序列进行改造，以实际工程案例为基础数据，生成改进GM（1，1）模型，并对现金流进行预测。结果显示改进后的GM（1，1）模型的预测较传统GM（1，1）模型具有较高精度，可实现建筑工程现金流的有效预测，从而提高建筑企业投资和融资决策的准确性；在施工过程中也可以提高成本预见性，从而加强成本控制，提高工程实施过程中资金管理的能力和效果。

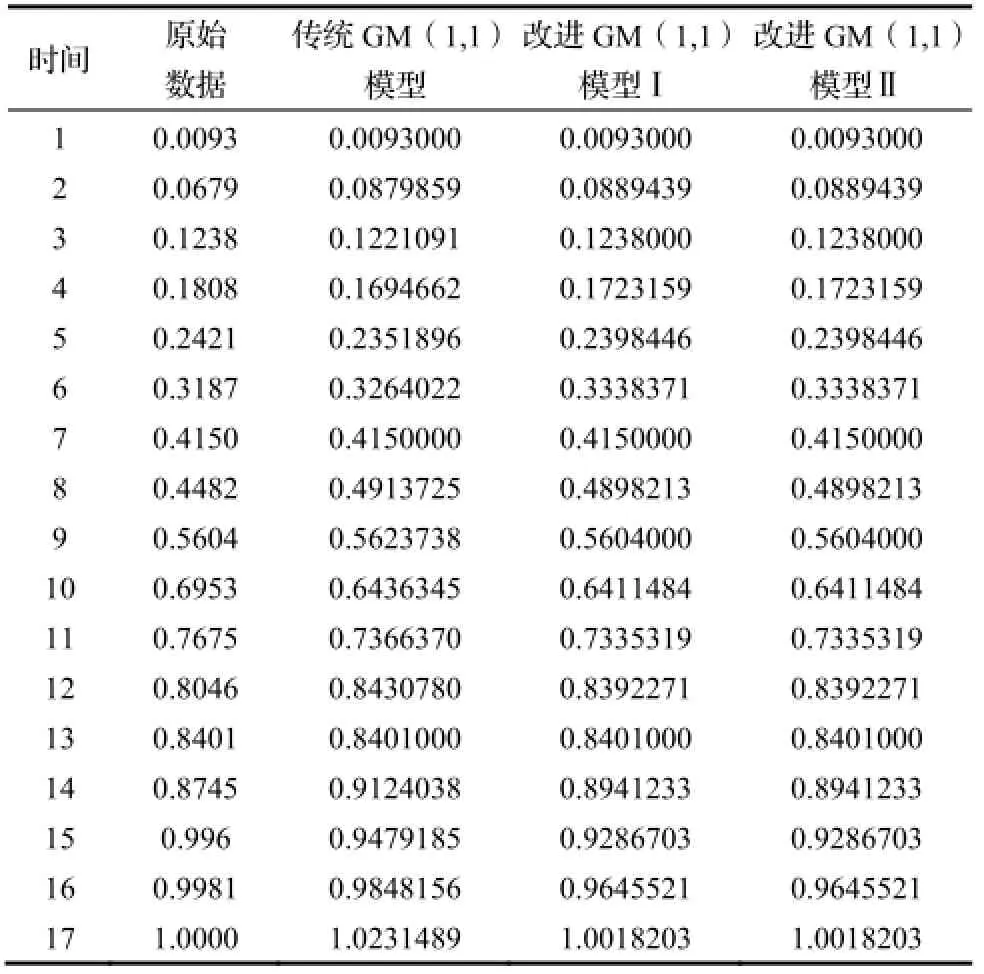
表4　实例2数据

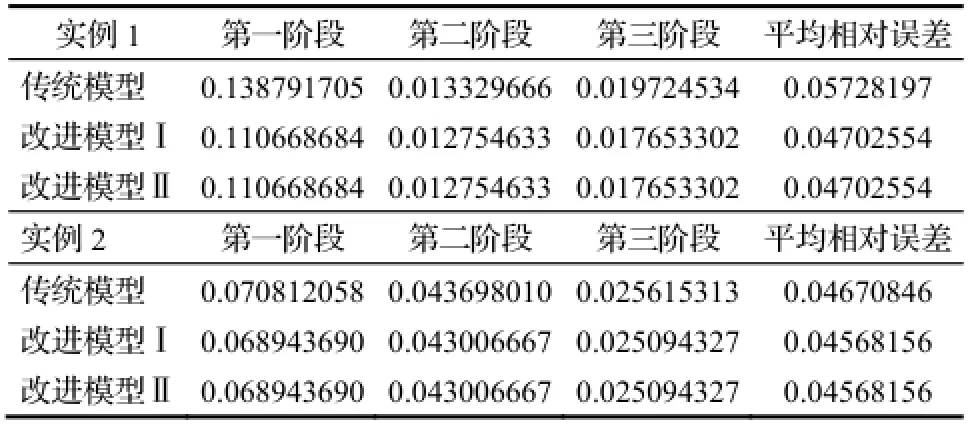
表5　三类预测精度应用结果误差表

［1］Gates M，Scarpa A.Preliminary Cumulative Cash Flow Analysis［J］.Cost Engineering，1979（6）:243-249.

［2］ Peer S.Application of Cost-flow Forecasting Models［J］.Construction Division，1982（2）:226-232.

［3］ Hudson K W.DHSS Expenditure Forecasting Method［J］. Chartered Surveyor Building and Quantity Surveying Quarterly，1978（3）:42-45.

［4］ Berny J，Howes R.Project Management Control Using Real-time Budgeting and Forecasting Models［J］. Construction Papers，1982（1）:19-40.

［5］ Boussabaine A H，Kaka A P.Anural Networks Approach for Cost Flow Forecasting［J］.Construction Management and Economics，1998（4）:471-479.

［6］Kaka A P，Lewis J.Development of a Company-level Dynamic Cash Flow Forecasting Model［J］.Construction Management and Economics，2003（7）:693-705.

［7］ Barraza G A，Back W E，Mata F.Probabilistic Forecasting of Project Performance Using Stochastic S curves［J］. Journal of Construction Engineering and Management，2004（1）:25-32.

［8］ Chao L C，Chien C F.Estimating Project S-curves Using Polynomial Function and Neural Networks［J］.Construction Engineering Management，2009，（3）:169-177.

［9］王伟红，赵 息，黄建通.建筑项目建设期现金流预测:基于移动权重法的新视角［J］.现代管理科学，2009（8）: 46-47.

［10］王 梅.房地产项目现金流管理研究［D］.西安:西安建筑科技大学，2013.

［11］刘文杰.房地产开发项目现金流预测初探［J］.财务与管理，2012（2）:16-17.

［12］彭 露.A房地产项目开发现金流规划研究［D］.广州:华南理工大学，2014.

［13］ Gates M，Scarpa A.Preliminary Cumulative Cash Flow Analysis［J］.Cost Engineering，1979（6）:243-249. ［14］邓聚龙.灰理论基础［M］.武汉:华中科技大学出版社，2002.

［15］向跃霖.废气排放量灰色建模初探［J］.环境科学研究，1995（6）:45-48.

［16］谢开贵，李春燕.基于遗传算法的GM（1，1）模型［J］.系统工程学报，2000（2）:168-172.

［17］王义闹，刘光珍，刘开第.GM（1，1）模型的一种逐步优化直接建模法［J］.系统工程理论与实践，2000（9）: 99-104.

［18］曾 波，孟 伟，王正新.灰色预测系统建模对象拓展研究［M］.北京:科学出版社，2014.

Application of Improved GM（1，1）Model to Forecast Cash Flow in Construction Projects

YU Jin-ping1，WANG Yin2，GAO Ping1
（1.School of Investment & Construction Management，Dongbei University of Finance and Economics，Dalian 116025，China，E-mail:lnuyujinping@163.com；2. Hangzhou Water Holding Group Co.，LTD，Hangzhou 310000，China）

Accurate construction project cash flow forecast can improve the effect of investment and financing decision，and it's the premise of stable revenues. Reasonable cash flow forecast method is a key to ensure the accuracy of the prediction results. This paper introduces the grey prediction and forecast cash flow “1/4:1/3” theory，based on the background of the weighting factor value structure，and collects more than 10 construction projects as sample，uses the golden section method and binary segmentation method of GM（1，1）model（grey forecasting model）to improve the applicability and adaptability of the construction project cash flow forecast practice. The empirical results show that the improved grey prediction model can be estimated with high precision， thus it can provide a reliable basis for corporate investment，financing decisions and capital management.

GM（1，1）model；construction project；cash flow forecast

TU723.3

A

1674-8859（2016）04-110-06

10.13991/j.cnki.jem.2016.04.021

于津苹（1992-），女，硕士研究生，研究方向:工程造价；

汪 茵（1989-），女，助理工程师，研究方向:工程造价，工程管理；

高 平（1961-），男，副教授，研究方向:工程造价，工程价值管理，工程合同管理。

2016-06-13.