用于风机新型叶片设计的典型仿鸮翼翼型气动性能研究*

李 典 刘小民/西安交通大学能源与动力工程学院



用于风机新型叶片设计的典型仿鸮翼翼型气动性能研究*

李 典 刘小民/西安交通大学能源与动力工程学院

Abstract

基于对低雷诺数下仿鸮翼型高效低噪特性的研究，为设计新型风机仿生翼型叶片提供理论参考。本文通过建立长耳鸮翅膀三维模型，并进行非定常数值计算。升阻力系数曲线显示了在小攻角下长耳鸮翅膀具有高升阻比特性。瞬态流场的计算结果表明：长耳鸮翅膀上表面靠近翼根的凸起区域存在明显的负压区，上下表面出现高压差，说明飞行时的升力主要来源于翼根处。在大攻角下，随着截面翼型厚度不断变薄，前缘弯度逐渐减小，在靠近翼尖的位置，尾流漩涡越来越大，致使诱导阻力也逐渐增加，整个上表面靠近翼尖的翼型附近产生了明显的不规则涡结构。

仿生设计；翼型；长耳鸮；大涡模拟

0 引言

风机叶轮气动性能是决定风机性能好坏的主要因素，而叶轮叶片剖面形状（翼型）又是决定叶轮性能的关键。目前，风机翼型叶片设计主要是参照飞机机翼翼型［1］，但飞机机翼翼型一般适用于高雷诺数下流动，具有一定的局限性，简单采用航空的已有翼型作为风机叶轮叶片形状，并不能充分发挥翼型叶片的优势。

研究发现，鸮类低速飞行所消耗的能量远小于其他鸟类，长耳鸮在飞行过程中还具有静音飞行的特性，对于改善风机叶片的气动性能和声学特性具有借鉴意义，为提高风机性能、降低风机噪声提供了新的研究思路和方法。其中Lilley［2］等对仓鸮、大林鸮在捕食过程中的滑翔飞行及扑翼飞行过程进行研究，发现其前缘梳状、尾缘“刘海”状结构是其降噪的主要特征元素。Kondo K［3］等利用三维隐式大涡模拟的方法对低雷诺数下的40%截面处鸮翼进行数值模拟，结果表明鸮翼的升阻比较NACA0002和NACA0012等标准翼型均有提高。葛长江［4］等对二维仿生翼型模型数值模拟后，由瞬态流场得到的声场显示出仿生翼型的声源具有偶极子特性，且最大的声源强度出现在后缘，揭露了仿生翼型的噪声机理。

将仿生技术应用在风机叶片设计中已取得了一定的成果，其中廖庚华［5］等通过提取的雀鹰、长耳鸮翅膀的表面特征对小型轴流风机的叶片进行仿生优化，结果表明仿生风机气动性能优于原型风机，最大质量流量提高了6.1%，最大静压提高了7.0%。孙少明［6］等设计了仿生前缘非光滑轴流风机叶片，仿生非光滑叶片在 50～2 000Hz的频段上噪声值明显小于原型风机叶片，最大降噪率为2.52%。刘小民［7］等分别对仿生尾缘锯齿叶片和标准叶片的流道模型进行了三维流场及声场的数值计算，结果表明仿生尾缘锯齿结构叶片的总A计权声压级比标准叶片降低了9.8dB。

基于长耳鸮的低雷诺数下高效飞行与风机叶片通常在低速、高升力系数下运行的工况相似性，本文利用逆向工程技术拟合出长耳鸮三维模型，提取鸮翼模型20%、40%、60%、80%典型截面处翼型，结合翅膀整体模型，通过利用Fluent商业软件对三维流场进行数值模拟，分析其优良气动性能的原因，结果对如何选取仿生翼型风机叶片具有重要的工程意义和学术价值。

1 三维模型提取

本文根据廖庚华［8］等通过三维激光扫描技术所得到的长耳鸮翅膀特征信息，首先通过提取长耳鸮不同截面处翼型，然后将各截面翼型曲线沿前缘线堆积，从而建立长耳鸮翅膀的三维模型。

不同截面翼型的上、下表面分别通过中弧线分布Z（c）及厚度分布Z（t）相加减得到，即方程（1）、（2）所示：

其中中弧线和厚度分布采用Birnbaum-Glauert函数方程，如下式所示：

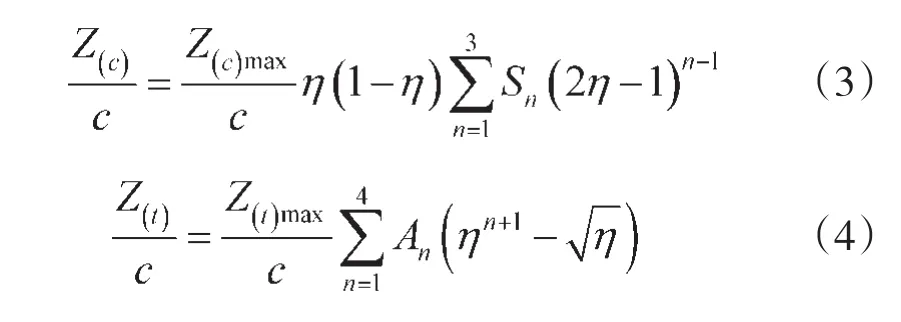
式中，c为翼型弦长，η=x/c为弦的相对位置坐标，Z（c）max为中弧线分布的最大值，Z（t）max为厚度分布的最大值，Sn和An是通过最小二乘法拟合得到的待定系数。其中S1=3.936 2，S2=-0.770 5，S3= 0.848 5，A1=-29.486 1，A2=66.456 5，A3=-59.806，A4=19.043 9。

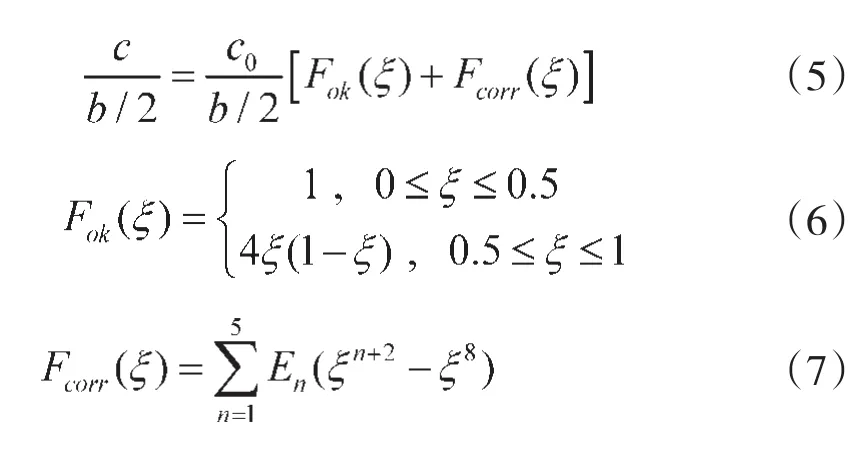
翅膀轮廓通过提取边缘点确定，根据轮廓线测量得出翼展方向弦长分布并依据式拟合确定系 数 E1=10.753，E2=-80.861，E3=245.298，E4=-367.73，E5=276.049。

对前缘点进行拟合，确定翅膀前缘拟合多项式为：

将计算出的各截面翼型曲线沿前缘线堆积便得到整个长耳鸮翅膀三维模型，图1为建好的长耳鸮三维翅膀模型图。

图1　长耳鸮三维翅膀模型图

2 数值计算

2.1 网格划分及边界条件

如图2所示，计算域采用30c×5c×8c的长方体区域，翅膀三维模型的近似平均弦长为c= 0.1m，翅膀模型展长约为2c，以翼根前端为原点，模型前缘距进口10c，距出口20c，上、下界均距模型4c，因模型边界为复杂几何外形，故采用非结构化网格，其对复杂边界有较强的适应性，对翅膀附近的网格进行细化加密处理，并施加边界层，保证壁面法向第一层网格y+＜1。图3为网格无关性验证示意图，分别采用24万、51万、139万、273万、314万网格在攻角为5°时进行网格无关性，可以得出当网格数大于273万时，升力系数变化小于1%，故这里采用273万网格进行计算，网格划分结果如图4所示。

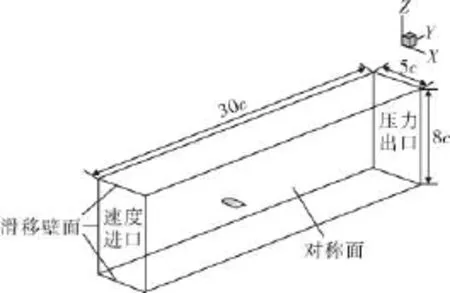
图2　计算域分布图

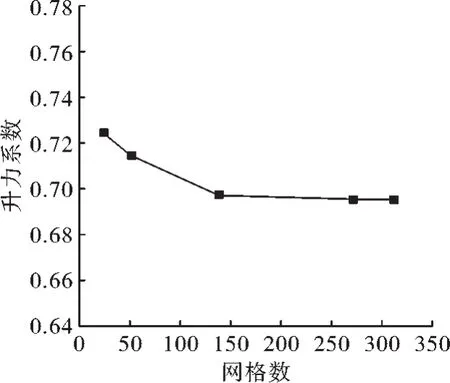
图3　网格无关性验证图

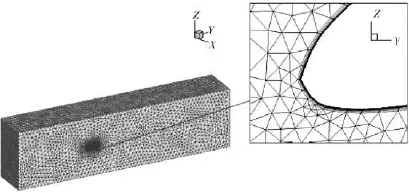
图4　网格划分示意图

本文以长耳鸮飞行的特征速度和一般风速为参考，结合离心风机内部流动的一般速度，将进口速度设为10m/s，弦长雷诺数约为70 000，出口绝对压力为1.013×105Pa，模型表面设为无滑移壁面边界条件，翼根处的界面设置为对称面，其余均设为滑移壁面边界条件，以减少壁面粘性的阻碍作用。

2.2 数值计算方法

本文采用Spalart-Allmaras单方程模型进行稳态计算，S-A模型是一种适应性很强的低雷诺数模型，计算量小且稳定性好，并可以保证一定的精度。将稳态计算收敛后的结果作为瞬态计算的初场。瞬态计算采用的是基于亚格子尺度模型的大涡模拟。

大涡模拟（LES）通过在傅里叶或空间域N-S方程滤掉时间项得到方程，可以有效的滤掉网格小的旋涡，从而获得大涡动量方程，过滤的变量可定义为：

式中，D为流场区域；G为决定过滤尺寸的函数。在Fluent中，离散化本身采用如下过滤操作：

式中，V为计算单元的体积，过滤函数G（X，X'）定义为

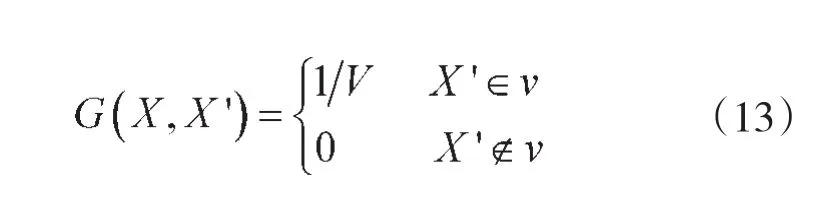
过滤不可压缩N-S方程，将得到：

式中，τkk为各项同性的亚格子应力，δij是克罗内克函数，μt为亚格子尺度的湍动粘度，一般用下式表示：

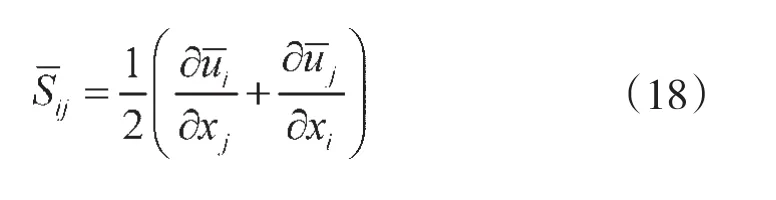
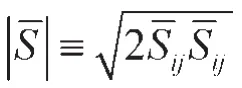
式中，ka为von Kármán常数；d为到壁面的最小距离；Cs为Samagorinsky常数，常取Cs=0.1。

瞬态计算的数值方法是基于有限体积法的SIMPLE算法，采用Green-Gauss Node Based梯度格式，为降低解的数值耗散的影响，离散格式均取二阶迎风格式。瞬态计算选取的时间步长为1×10-5s。

2.3 计算方法验证

对长耳鸮模型在不同攻角下、雷诺数为16 000时进行数值模拟，以验证本文计算方法的可靠性。图5为本研究方法定常计算结果的升力系数曲线与文献中［9］实验值的对比结果，由图5中可知，因在实验过程中翅膀发生一定程度的形变，使实验结果与数值计算有一定的偏差，但整体与实验值吻合较好。

图5　Re=16 000时升力系数曲线图

3 计算结果分析

3.1 升阻比分析

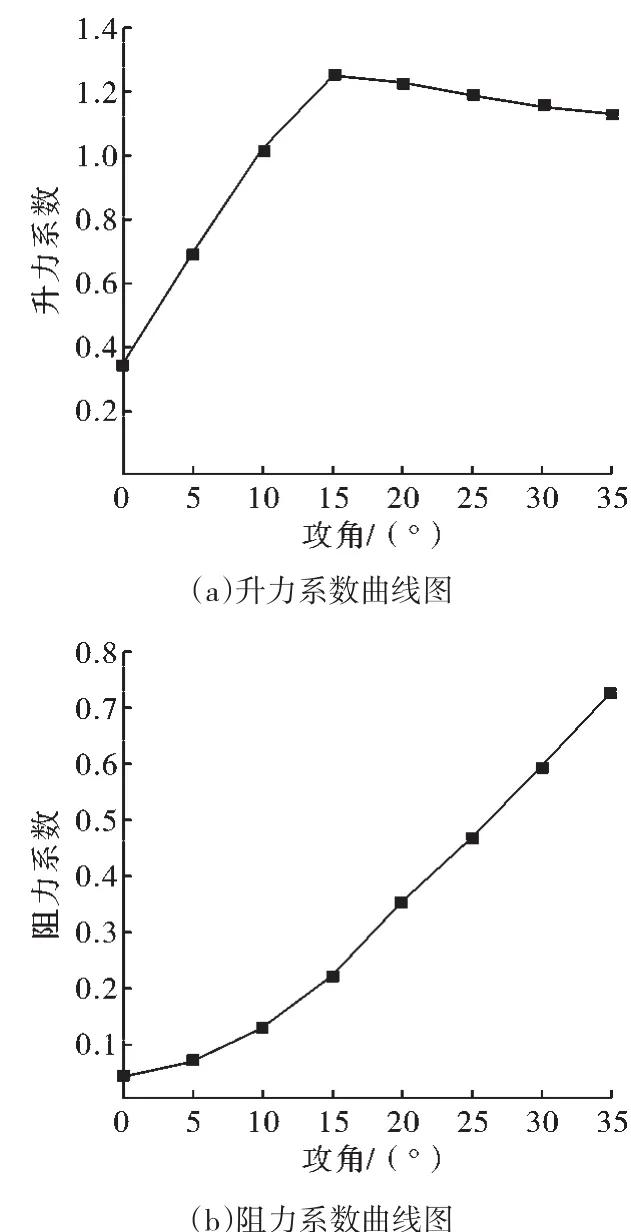
图6 升阻力曲线图

图6为0°到35°攻角下的升力系数及阻力系数曲线，由图6（a）可知，由于翅膀弯度较大，气流在小攻角时绕翅膀流动，上下表面流速差大，压差大进而产生了升力，升力系数随攻角的增加而明显增大，并在15°左右达到峰值，当攻角大于15°时，升力系数逐渐下降，这是由于翅膀表面上的流动会向紊流过渡，同时会加剧边界层的分离，导致翅膀上下表面的压力差减小，升力减小，但由于长耳鸮翅膀的特殊结构，升力大小下降趋势较缓，升力系数降低程度并不明显，此时翅膀仍具有较高的升力系数。图6（b）为阻力系数随攻角的变化曲线，随着攻角逐渐增加，气流在翼型表面上的流动出现了分离，从而压力变小，阻力系数增加。最初阻力系数随攻角增幅较缓，之后由于在大攻角下翅膀的尾缘附近出现了尾随涡，翅膀上下表面产生较大的压差阻力。而由于大攻角下气流的冲击作用，使得下表面流速过快，上下表面压力差增大，当气流与翅膀表面接触时亦会产生较大的摩擦阻力，进而加快了阻力系数的增加。总体来讲，长耳鸮翅膀具有高升力系数特性，能完全满足风机叶片运行所需的高升力系数条件。

图7　0°攻角下不同截面处速度云图及流线分布图

图8　20°攻角下不同截面处速度云图及流线分布图

3.2 速度分布

为了进一步分析流场的流动状态，包括翼型叶片在小攻角及大攻角下的流动状态，结合长耳鸮水平飞行及起飞、捕食等特殊飞行姿态，给出了攻角为0°及20°下长耳鸮翅膀模型20%、40%、60%、80%处截面的速度云图及流线图，如图7、图8所示，当来流攻角为0°，气流流经翅膀上表面时，贴近翅膀表面的气流形成了先减速后加速的流动特点，在20%截面处，速度在上表面前缘凸起部分处达到最大，而下表面亦由于下凸状的特殊结构，在气流流过时，无法保持附面流动，且由于空气粘性致使贴近上表面气流流向下表面速度低的区域，而下表面的气流流向相反方向并将边界层卷起、拉伸形成旋涡，并增加了诱导阻力。在40%、60%、80%截面处翼型均可保持附面流动，几乎没有发生负面层分离，这是由于随着截面由翼根到翼尖沿展向的变化，翅膀的弯度逐渐减小，使得气流流动过程中阻力减小，加快了边界层的流速，使气流紧贴于翅翼表面从而抑制了边界层的分离，并相应的减少回流，有效的延迟了失速现象的发生，且抑制了诱导阻力的产生。当来流攻角为20°时，气流在吸力面上产生了明显的旋涡区域，并随着截面沿展向的变化，其位置和大小均发生显著变化。流线清晰的显示了旋涡区与气流的低速区变化基本一致，说明翅膀上表面的上弯结构可以改变涡旋脱落的位置，在20%截面处，其涡旋位于尾缘处附近，且吸力面前缘局部高速区的速度达到峰值，在40%截面处，出现了一大一小两个涡旋，并且大涡向前缘迁移并远离上表面。在60%、80%截面处，由于此处翅膀前缘并不“光顺”，使气流不能紧贴表面流动并产生大尺寸涡，而旋涡区域逐渐前移并到达前缘位置。在大攻角下，随着截面翼型厚度不断变薄，前缘弯度逐渐减小，在靠近翼尖的位置，尾流的旋涡越来越大，致使诱导阻力也逐渐增加。且相比于其他截面翼型，40%截面处翼型可以改变旋涡的位置，增大涡间距离，减小尾迹涡的范围，从而降低翼型表面的压力脉动，使噪声显著减小。

图9　不同攻角下压力云图

3.3 压力分布

图9为0°及20°攻角下翅膀模型表面及翅膀展向20%、40%、60%、80%截面处的压力云图，图中清晰的显示了在不同攻角下由于气流的冲击翅膀表面的压力变化规律。通过比较各截面的压力云图可以发现，当气流攻角为0°时，翅膀前缘由于弯度较大，在气流的冲击下产生局部高压区，各截面的高压区域沿来流方向扩散并减弱，其范围随沿展向到翼尖的截面变化而逐渐减小，根部翅膀的上表面凸起区域明显存在一小范围的负压区，故可以产生较大的升力，负压区由翼根到翼尖沿展向逐渐减小，并在40%展长处基本消失，说明飞行时的升力主要来源于翼根处，进一步验证了靠近翼根处截面的翼型是长耳鸮翅膀具有高升力系数的主因。当气流攻角为20°时，气流流过时无法产生绕翅膀的附体流动，由于来流方向的改变，气流冲击对长耳鸮翅膀产生的局部高压区出现在翅膀前缘的下表面，且高压区域的范围比在小攻角下时要大，各截面局部高压区沿展向变化较缓，在80%截面处仍能清晰的显示出高压区的位置及大小，压力面高压区域的扩大说明由于大攻角下气流冲击产生的压力高，使得长耳鸮翅膀产生更高的升力，但同时也产生了较大的压差阻力。吸力面翅膀根部附近的负压区中心移至翅膀前缘，在翅膀表面产生边界层分离。气流流经长耳鸮翅膀上表面后，各截面压力云图清晰的显示了在吸力面上方出现了大范围的负压区，且在20%截面处负压区的中心位于翅膀尾缘的延伸区，说明此处的气流分离严重，随着沿展向截面的变化，负压区的中心向前缘迁移，并在80%截面处到达翅膀中游位置，这与速度云图及流线图观测出来的涡结构位置的变化规律一致。攻角变化而导致长耳鸮翅膀吸力面上的流动恶化是产生分离涡结构的主要原因。

3.4 涡结构分布

利用第二不变量Q［10］的等值面来描述瞬间涡流结构的方法，是描述三维瞬态数据的最佳可视化技术，因此本文采用Q判据对气流攻角为0°及20°时绕鸮翼三维瞬态流场下的涡结构进行分析。如图10所示，Q的等值面［11］代表瞬态流场下的分离涡结构。当攻角为0°时，气流流过时由于翅膀的特殊结构，使气流在下表面壁面附近形成一定范围的气流旋涡区域，气流在贴近压力面前缘处开始分离，分离程度很小，随着分离气泡向下游迁移，分离区域逐渐增大，但此时边界层流动分离仍不明显。翅膀模型吸力面的边界层几乎不发生分离，气流流过上表面时始终保持附体流动，在尾缘处才逐渐形成小区域的尾迹涡。当攻角为20°时，压力面受到气流的冲击，形成一定的压力迫使气流沿展向流动，与0°攻角相比加快了压力面分离区内的流速，从而减小了压力梯度，抑制了边界层的分离，故无明显的涡结构产生。流过吸力面的气流从0.2c处开始分离，并沿弦向分离气泡逐渐增大，诱导出更大的旋涡，整个上表面尤其是靠近翼尖的翼型附近由于剪切层的开尔文-亥姆霍兹（K-H）不稳定性［12］产生了明显的不规则涡结构，临近尾缘处的大尺度涡逐渐饱和并在脱离尾缘处发生涡结构的破碎，转化为小尺度湍流，而靠近翼根附近的翼型则影响较小。

图10　瞬态流场下的涡结构示意图

4 结论

本文采用数值计算的方法对长耳鸮翅膀三维模型的气动性能进行了数值计算，并给出了典型截面处翼型附近的流场分布，研究结果表明：

1）升力系数随攻角变化的趋势为先升后降，并在15°左右时达到峰值，之后缓慢下降，但仍具有较高的升力系数，说明长耳鸮翅膀整体具有高升力系数特性。瞬态流场的计算结果表明：长耳鸮翅膀上表面靠近翼根的凸起区域存在明显的负压区，上下表面出现高压差，说明飞行时的升力主要来源于翼根处，进一步验证了靠近翼根处截面的翼型是长耳鸮翅膀具有高升力系数的主要原因。

2）相比于其他截面翼型，40%截面处翼型可以改变旋涡的位置，增大涡间距离，减小尾迹涡的范围，从而降低翼型表面的压力脉动，使噪声显著减小。在大攻角下，气流冲击使下表面获得较高压力，使得长耳鸮翅膀产生更高的升力，但同时也导致了较大的压差阻力，随着截面翼型厚度不断变薄，前缘弯度逐渐减小，在靠近翼尖的位置，尾流的旋涡越来越大，致使诱导阻力也逐渐增加，整个上表面尤其是靠近翼尖的翼型附近产生了明显的不规则涡结构，而靠近翼根附近的翼型则影响较小。故攻角变化而导致长耳鸮翅膀吸力面靠近翼尖附近的流动恶化是产生分离涡结构的主要原因。

3）本文的计算结果初步揭示仿鸮翼型具有优良气动性能的原因，并提供了四种典型的厚薄截面翼型的分析结果，对风机新型翼型叶片设计具有参考价值。

［1］席德科，杨青.先进翼型与先进翼型风机的设计与实验研究［J］.流体机械，2000，28（4）：5-9.

［2］Lilley GM.A study of the silent flightof theowl［J］.AIAA paper，1998，2340（1998）：l-6.

［3］Kondo K，Aono H，Nonomura T，etal.Large-Eddy Simulations of Owl-Like Wing Under Low Reynolds Number Conditions［C］// ASME 2013 Fluids Engineering Division Summer Meeting. American Society of Mechanical Engineers， 2013： V01AT04A004-V01AT04A004.

［4］葛长江，葛美辰，梁平，等.基于鸮翼的仿生翼型噪声机理研究［J］.农业机械学报，2013（S1）：292-296.

［5］廖庚华，胡钦超，杨莹，等.基于典型鸟类翅膀特征的小型轴流风机叶片仿生设计与试验［J］.吉林大学学报：工学版，2012，42（5）：1163-1167.

［6］孙少明，徐成宇，任露泉，等.轴流风机仿生叶片降噪试验研究及机理分析［J］.吉林大学学报：工学版，2009（2）：382-387.

［7］刘小民，汤虎，王星，等.苍鹰翼尾缘结构的单元仿生叶片降噪机理研究［J］.西安交通大学学报，2012，46（1）：35-41.

［8］廖庚华，杨莹，胡钦超，等.长耳鸮翅膀的三维建模［J］.吉林大学学报：工学版，2012（S1）：423-427.

［9］廖庚华.长耳鸮翅膀气动与声学特性及其仿生应用研究［D］.吉林大学，2013.

［10］Hunt JCR，Wray A A，Moin P.Eddies，streams，and convergence zones in turbulent flows［J］.1988.

［11］Kim T，Jeon M，Lee S，etal.Numerical simulation of flatback airfoil aerodynamic noise［J］.Renewable Energy，2014，65：192-201.

［12］付斐，叶建.低雷诺数翼型分离流动的大涡模拟研究［J］.聊城大学学报：自然科学版，2014，27（3）：61-67.

Aerodynam ic Performance of Typical Bionic Ow l-based Airfoil App lied on Design of Fan Blade

Li Dian，Liu Xiao-min/School of Energy and Power Engineering，Xi’an Jiaotong University

To develop a new bionic fan blade with high efficiency and low noise characteristics，the long-eared owl wing was researched under low Reynolds Number.The three-dimensional modeling of the long-eared owlwing was established to carry out the unsteady numerical simulation.The lift and drag coefficients curve showed that the long-eared owlwing had considerably high lift-to-drag ratio. The results indicated that the cause of the long-eared owl wings with high lift coefficientwas the airfoilnear thewing root which demonstrably created a negative pressure zone on the upper-surface and differential pressure between up with down surface.The leading edge camber of the airfoil decreased gradually with the thickness of the airfoil constantly became thinner under a large angle of attack.The induced drag increased gradually due to the range of vortex becamingwider near the location of the wingtip.Resulting in the obviously vortex structure on the whole upper-surface of the airfoil especially near thewingtip.

bionics design；airfoil；longeared owl；large eddy simulation

TK05；TH432.1

A

1006-8155（2016）01-0022-08

10.16492/j.fjjs.2016.01.0068

高等学校博士学科点专项科研基金项目（20120201110064）；陕西省科学技术研究发展计划项目（项目编号：2014K06-24）

2015-04-30 陕西 西安 710049