正定矩阵合同对角化的一个简洁方法及其应用

冯爱芳,　刘祖华,,　郭聿琦

(1.昆明学院数学系，昆明650214;　2.兰州大学数学与统计学院，兰州730000)



正定矩阵合同对角化的一个简洁方法及其应用

冯爱芳1,刘祖华1,2,郭聿琦2

(1.昆明学院数学系，昆明650214;2.兰州大学数学与统计学院，兰州730000)

利用正定矩阵的性质, 给出一个“求可逆矩阵P， 将正定矩阵A合同对角化”的简洁方法，给出该方法在化正定二次型为标准形和求标准正交基底中的应用.

正定矩阵; 合同对角化; 正定二次型; 标准正交基底

高等代数是本科数学类专业的必修课, 对学生完成其他专业课程的学习具有基础性的作用. 因此, 对该课程中某些重要内容作些深入的研究是非常必要的[1-3]. 正定矩阵是一类重要的矩阵, 在“高等代数”中占有重要地位, 其理论有着丰富的内容, 正定二次型以及欧氏空间的相关内容都与之有关. 本文关于正定矩阵的合同对角化问题作进一步研究.

首先, 我们给出一些基本概念和事实.

1　基本概念和事实

定义1[4]令F为一数域, A,B∈Fn×n. 称A与B合同, 如果存在F上可逆矩阵P, 使得

B=P′AP.

若矩阵A与一个对角阵合同, 则称A可合同对角化.

定义2[4]令A∈Rn×n. 称A为正定矩阵, 如果存在实可逆矩阵Q , 使得

A=Q′Q.

显然, 正定矩阵是对称的, 且与单位矩阵合同. 因此, 正定矩阵可合同对角化.

关于实对称矩阵的正定性, 有以下基本事实:

定理3[4]令A∈Rn×n, A′=A. 则以下几条等价:

(i) A是正定的;

(ii) 存在实可逆矩阵P, 使得P′AP=Ddi,n, 其中Ddi,n为对角线元素为d1,d2,…,dn的对角阵,di>0,i=1,2,…,n;

(iii) A的所有顺序主子式均大于零;

(iv) 实n元二次型f(x1,x2,…,xn)=X′AX为正定二次型(即关于任意一组不全为零的实数(c1,c2,…,cn), 都有f(c1,c2,…,cn)>0).

定理3的(ii)中的矩阵P可逆, 从而P是若干初等矩阵的乘积, 不妨令

P=P1P2…Ps,

其中Pi为初等矩阵,i=1,2,…,s,s∈+. 则

P′s…P′2P′1AP1P2…Ps=P′AP=Ddi,n.

定义4令A∈Fn×n, P为一初等矩阵. 则P′AP表示关于矩阵A施行一对行列对偶的初等变换. 称这一对初等变换为一个初等合同变换.

因此有

定理5[4]任意n阶对称矩阵(特别地, 正定矩阵)常可经由有限次初等合同变换化为对角阵.

2　正定矩阵合同对角化的一个简洁方法

下面为了陈述的方便,先交代三个初等矩阵的记号.

显然

令

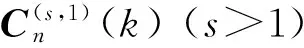
其中Pi,i=1,2,…,n-1均为上三角阵, 并且容易验证

由A为正定矩阵知, P′n-1…P′2P′1AP1P2…Pn-1为正定矩阵, 从而P′n-1…P′2P′1AP1P2…Pn-1的所有顺序主子式Δk全都大于零,k=1,2,…,n. 而容易验证

Δ1=a11>0,Δk+1=a11Δ′k>0,k=1,2,…,n-1,

其中Δ′k为A1的全部顺序主子式,k=1,2,…,n-1, 因此

Δ′k>0,k=1,2,…,n-1,

为上三角矩阵, 并且

因此, 有

为上三角阵, 且

根据定理6, 求可逆矩阵P, 将正定矩阵A合同对角化的方法步骤如下:

(i) 构作矩阵C=(A,E);

D=(M,N),

其中M是对角线元素分别为d1,d2,…,dn的上三角矩阵;

(iii) 令P=N′. 则P′AP=Ddi,n.

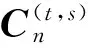
3　正定二次型合同对角化的两个应用

下面我们以在两个方面的应用来体现该方法的优越性.

(i) 化正定二次型为标准形

正定二次型与正定矩阵一一对应,实二次型正定当且仅当其对应的二次型矩阵正定. 并且一个二次型经由变数的可逆线性替换后所得新二次型的二次型矩阵与原二次型矩阵合同. 因此, 化正定二次型为标准形的问题就归结到正定矩阵的合同对角化问题上来.

例1化正定二次型

为标准形, 并给出相应的变数的可逆线性替换.

解显然, 二次型矩阵

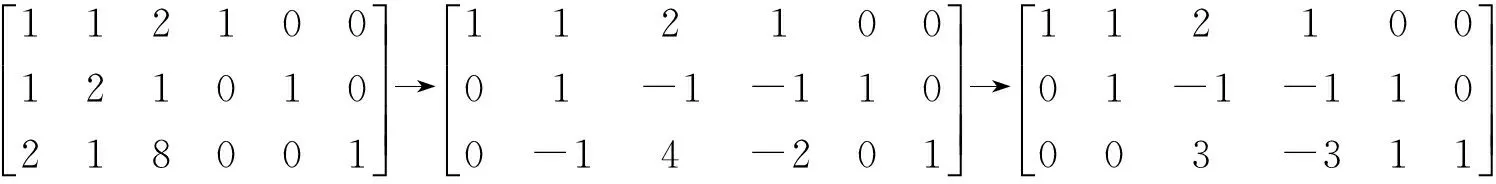
令

则

(ii) 求标准正交基底

传统的求有限维欧氏空间标准正交基底的方法是Schmidt正交化方法, 其特点是逐个扩充, 层次分明, 但计算繁琐. 利用正定矩阵的合同对角化方法求标准正交基底则更为简洁.

定理8令V为一n维Euclid空间, A是其内积在基底(α1,α2,…,αn)下的度量矩阵. 则

(i) 存在实可逆矩阵P, 使得P′AP=Ddi,n;

(ii) 令

(β1,β2,…,βn)=(α1,α2,…,αn)P.

则(β1,β2,…,βn)是V的一个正交基底.

证(i) 因为A是内积在基底(α1,α2,…,αn)下的度量矩阵, 所以A是正定矩阵. 由定理3知, 存在实可逆矩阵P, 使得P′AP=Ddi,n.

(ii) 令

(β1,β2,…,βn)=(α1,α2,…,αn)P.

则由(α1,α2,…,αn)是基底, 和P可逆知, (β1,β2,…,βn)仍为基底, 且内积在其下的度量矩阵B满足

B=P′AP=Ddi,n.

于是, (β1,β2,…,βn)是V的一个正交基底.

根据定理6和定理8,得到求标准正交基底的方法步骤如下:

(i) 求出内积在基底(α1,α2,…,αn)下的度量矩阵A, 分别以α1,α2,…,αn为元素构作形式行向量B=(α1,α2,…,αn)；

D=[M,N]，

P′(A,B′)=(P′A,P′B′)=(M,N),

其中M为上三角矩阵, N=(BP)′；

(iii) 令β1,β2,…,βn为形式列向量N的n个元素(即形式行向量BP的n个元素). 则(β1,β2,…,βn)即是V的一个正交基底；

(iv) 将(β1,β2,…,βn)单位化为(γ1,γ2,…,γn), 则(γ1,γ2,…,γn)即为V的一个标准正交基底.

例2在Euclid空间R4中(关于通常内积), 将基底(α1,α2,α3,α4)标准正交化, 其中

α1=(1,1,0,0),α2=(1,0,1,0),α3=(-1,0,0,1),α4=(1,-1,-1,1).

解内积在基底(α1,α2,α3,α4)下的度量矩阵A, 和以α1,α2,α3,α4为元素构作的形式行向量B分别为

则

即为R4的一个正交基底. 再将(β1,β2,β3,β4)单位化, 即令

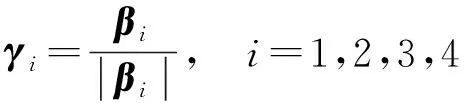
则

即为R4的一个标准正交基底.

注一般地, 关于任意实对称矩阵A, 满足

P′AP=Ddi,n

的可逆矩阵P未必是上三角矩阵, 从而

P′A=Ddi,nP-1

未必是上三角矩阵. 因此, 关于(A,E)仅施行有限次第二种初等行变换时, 并没有一个明确的目标, 我们不知道要将A化到什么状态才能停止施行变换. 例如, 令

关于(A,E)仅施行第二种初等行变换, 化为

此时

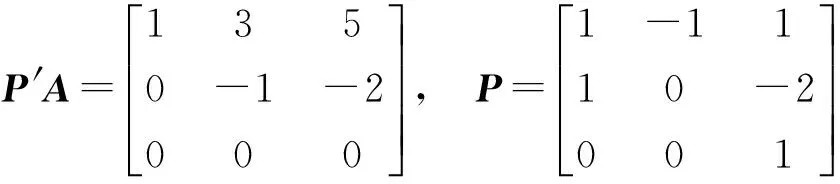
虽然P′A为上三角阵, 但

不是对角阵.

[1]李尚志. 线性代数精彩应用案例(之一)[J]. 大学数学，2006, 22(3): 1-8.

[2]李志慧, 梁斌. 利用矩阵的初等变换求方阵的特征值[J]. 大学数学, 2007, 23(4): 167-171.

[3]郭聿琦, 王正攀, 刘国新. 谈谈“高观点下的初等数学”—以基础代数学为例[J]. 大学数学， 2011, 27(1): 4-7.

[4]郭聿琦, 岑嘉评, 王正攀. 高等代数教程[M].北京: 科学出版社,2014.

The Simple Method for the Congruent Diagonalization of the Positive Definite Matrixs and the Applications

FENG Ai-fang1,LIU Zu-hua1,2， GUO Yu-qi2

(1. Department of Mathematics ,Kunming University, Kunming 650214, China;2. Department of Mathematics and Statistics,Lanzhou University, Lanzhou 730000, China)

By using the properties of the positive definite matrix, the simple method for getting the inverse maxtrix Pcongruent diagonalize the positive definite matrix A are given .And the applications to change the positive definite quadratic forminto the canonical form, and solve the standard orthogonal basis are given.

positive definite matrix; congruent diagonalization; positive definite quadratic form; standard orthogonal basis

2015-11-19；[修改日期]2016-04-01

云南省教育厅科学研究基金项目(2015Y392)

冯爱芳(1981-)，女，副教授，从事群论研究. Email: fengaifang888@sina.com

O153

C

1672-1454(2016)04-0091-06