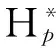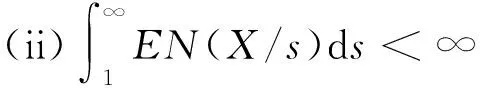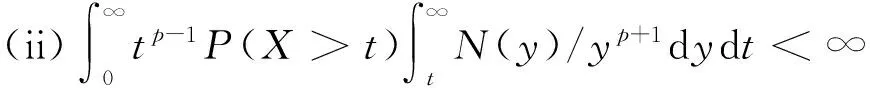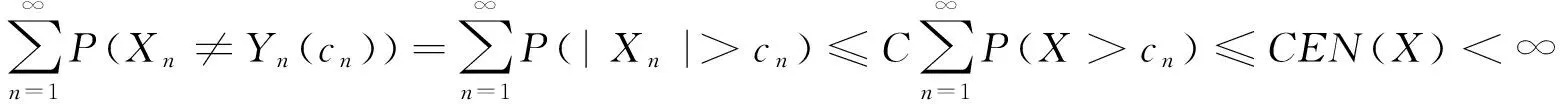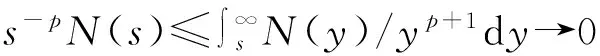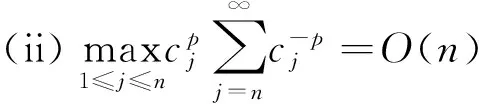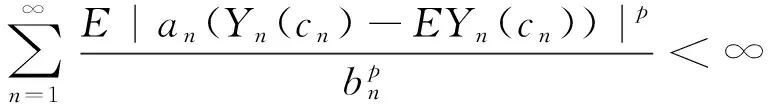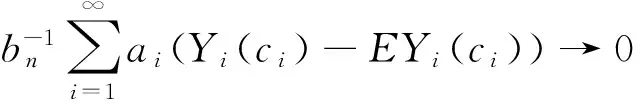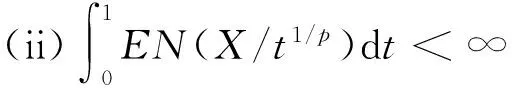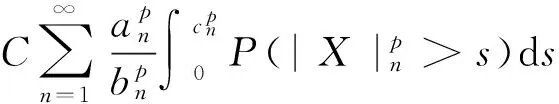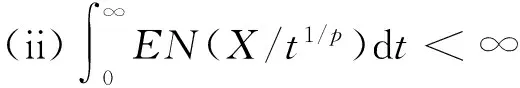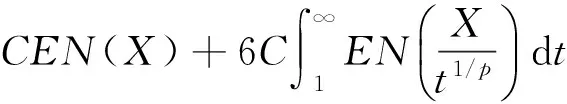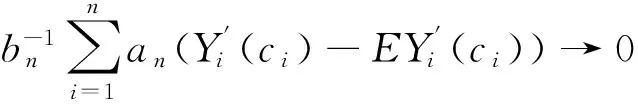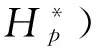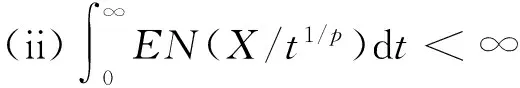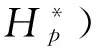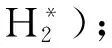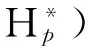一类随机变量序列线性形式的强稳定性
2016-09-23万成高李艺璇邢韵
万成高, 李艺璇, 邢韵
(湖北大学数学与统计学学院,湖北 武汉 430062)
一类随机变量序列线性形式的强稳定性
万成高, 李艺璇, 邢韵
(湖北大学数学与统计学学院,湖北 武汉 430062)
研究一类随机变量序列线性形式的强稳定性,得到这类随机变量序列具有线性形式强稳定性的充分条件.
随机变量序列;线性形式;强稳定性
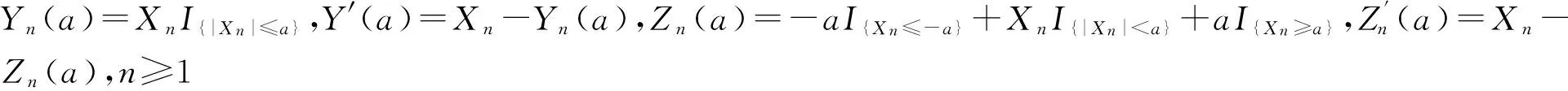
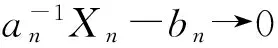
称随机变量序列{Xn,n≥1}是尾概率一致有界的,若存在非负的随机变量X及正常数C,使对任意的x及n≥1,都有P(|Xn|>x)≤CP(X>x)成立,此时记为{Xn} 约定:文中出现的C总表示正常数,它在不同的地方可以代表不同的值.IA表示集合A的示性函数.记 引理1设X为随机变量,且对任意的x>0,都有P(|X|>x)≤CP(V>x),其中V为非负随机变量,C>0为常数,则对任意的x>0,q>0,有E|X|qI{|X|≤x}≤CxqP(V>x)+CEVqI{V≤x}. 有 引理2设{an,n≥1}和{bn,n≥1}是任意的两个正实数列,cn=bn/an,bn↑∞,{Xn,n≥1}为零均值的随机变量序列且{Xn} (i)EN(X)<∞; 引理2的证明因为 由Kronecker引理知引理2的结论成立. (i)EN(X)<∞; 由于 由引理1有 因此有 (1) 以及 (2) 上面最后一个不等式成立基于下列事实: 推论1的证明由定理1及引理2即得. (i)EN(X)<∞; 定理2的证明只证{Xn,n≥1}⊂Hp的情形.由于 由引理1有 (3) (4) (i)EN(X)<∞; 由于 (i)EN(X)<∞; 由条件(i),(ii)有 (i)EN(X)<∞; 下文中总是记α(x):→是正的非降函数,且满足 (A)bn→∞; (C)xα(log+x),x>0是非降的. 定理5设{Xn,n≥1}是同分布的的随机变量序列,E|X1|α(log+|X1|)<∞,如果{Xn,n≥1}满足下列两条件之一: 定理5的证明因为0<α(x)↓,bn↑∞.由条件(B),可选取m0≥1,α>0,β<0使得当n≥m0时 αn≤cnα(logcn)≤βn (5) 于是有 (6) 从而有 (7) 先证(i),只证{Xn,n≥1}⊂H2的情形.对n≥m≥m0,由(5)式有cn≥αn(α(logcn))-1,从而 这里m≥m0.于是当m≥m0时有 O(1)+Cβα-2E|X1|α(log+|X1|)<∞, 再证(ii),同样只证{Xn,n≥1}⊂H1的情形.由于 (8) 取c0=0有 (9) 如果{Xn,n≥1}不是同分布的,我们有下面的结论. 定理6的证明只证{Xn,n≥1}⊂Hp的情形,并采用定理5同样的证明方法,易得 (3) 对ρ混合、φ混合等序列,当ρ(n)、φ(n)等满足一定条件时,其混合序列{Xn,n≥1}⊂Hp,其中1≤p≤2这里不一一列举. [1] Jamison B,Orey S,Pruitt W.Convergence of weighted averages of independent random variables[J].Z Wahrsch verw Gebiete,1965(1):40-44. [2] Chow Y S, Teicher H.Almost certain summability of independent,identically distributed random variables[J].Ann Math Statist,1971(3):401-404. [3] 王岳宝, 严继高.关于不同分布两两NQD列的Jamison 型加权乘积和的强稳定性[J].数学年刊,2001(3):701-706. [4] 甘师信.两两NQD列的强稳定性[J].数学物理学报,2008(4):612-618. [5] 王岳宝, 周斌, 苏淳.关于NA列部分和上升的阶[J].应用概率统计,1998(2):213-219. [6] 王瑶, 谭成良,吴群英,等.ρ-混合序列的Hajek-Renyi型不等式及其应用[J].数学的实践与认识,2011,41(13):152-158. (责任编辑赵燕) Strong stability of linear forms with a class of random variable series WAN Chenggao, LI Yixuan, XING Yun (Faculty of Mathematics and Statistics, Hubei University, Wuhan 430062,China) We discussed strong stability of linear forms in a class of random variable series and got sufficient conditions for strong stability of linear forms with this class of random variable series. random variable series;linear forms;strong stability 2016-02-18 国家自然科学基金(10571139)资助 万成高(1959-),男,教授 1000-2375(2016)05-0383-07 O211.4 A 10.3969/j.issn.1000-2375.2016.05.001