Mixed Finite Element Formats of any Order Based on Bubble Functions forStationary Stokes Problem

CAO Ji-wei，LIU Ming-fang，CHEN Shao-chun

（1.School of Mathematical Sciences，Nankai University，Tianjin 300071，China；2.College of Mathematics and Statistics，Henan University，Kaifeng 475000，China；3.College of Mathematics and Statistics，Zhengzhou University，Zhengzhou 450052，China）



Mixed Finite Element Formats of any Order Based on Bubble Functions for
Stationary Stokes Problem

CAO Ji-wei1，LIU Ming-fang2，CHEN Shao-chun3

（1.School of Mathematical Sciences，Nankai University，Tianjin 300071，China；2.College of Mathematics and Statistics，Henan University，Kaifeng 475000，China；3.College of Mathematics and Statistics，Zhengzhou University，Zhengzhou 450052，China）

Mixed element formats of any order based on bubble functions for the stationary Stokes problem are derived in triangular and tetrahedral meshes and the convergence of these formats are proved.

mixed finite element method；bubble function；the stationary Stokes problem

2000 MR Subject Classification:65N30，65N15

Article ID:1002—0462（2016）01—0087—09

Chin.Quart.J.of Math.

2016，31（1）：87—95

§1.　Introduction

Let Ω∈Rn（n=2，3）be the bounded polygonal domain.Consider the following Stokes problem

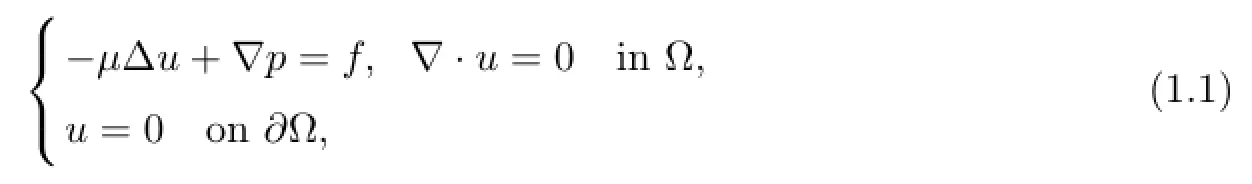
where u=（u1，u2，···，un）denotes the fluid velocity，p denotes the pressure andµ＞0 denotes the viscosity coefficient.And f=（f1，f2，···，fn）∈（L2（Ω））ndenotes the external force.

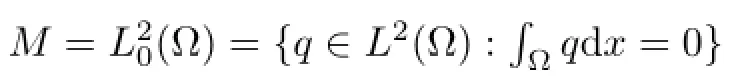
（u，p）∈H×M，such that

It’s obvious that a（u，v）satisfies the following coercivity condition on H：there exists a constant α＞0，such that

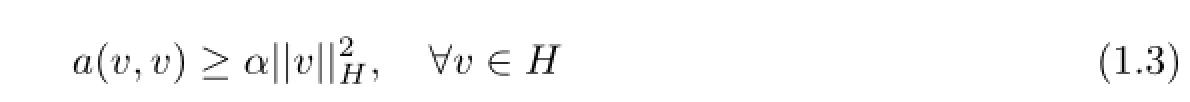
and b（v，q）satisfies Babuska-Brezzi condition（B-B condition for short）［1，2］，i.e.，there exists a constant β＞0，such that

Let Hhand Mhbe the discrete finite element spaces of H and M respectively and Ththe partition of Ω.then we have the discrete problem of（1.2）：Find（uh，ph）∈Hh×Mh，such that

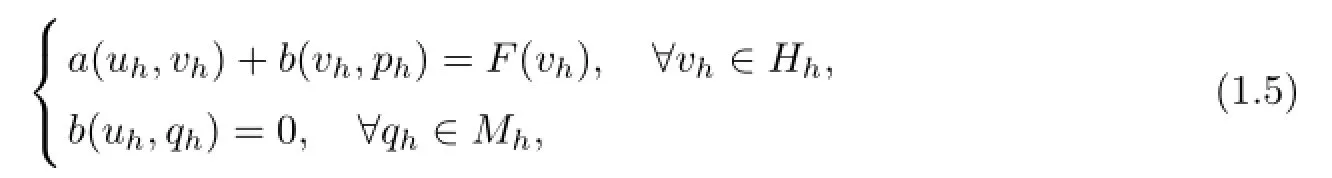
where

and b（vh，qh）satisfies the discrete Babuska-Brezzi condition［1，2］，i.e.，there exists β＞0，such that

Then the discrete mixed finite element problem（1.5）has an unique solution.

The stationary Stokes problem is an important and standard mixed problem，the velocity and pressure are solved at the same time.The difficulty to solve this problem with mixed finite element method is that the discrete Babuska-Brezzi condition（1.7）should be satisfied.In［4］，Crouzeix-Raviart element is used to solve the Stokes problem.Because bilinear element and linear element don’t satisfy the discrete B-B condition，use macro element skills and use the method of adding bubble functions to solve the Stokes problem in［3］and［5］respectively.In［6］，Bernardi and Raugel show the first order and the second order schemes based on bubble functions for Stokes problem.The results mentioned above are discussed in the pressure space M.In this paper，we will consider the Stokes problem based on bubble functions in the pressure space Q=｛q∈H1（Ω）：∫Ωqdx=0｝.

Function spaces involved in this paper are common Sobolev spaces.The norm and seminorm of Hk（Ω）are denoted，respectively，by||·||kand|·|k.Additionally，||·||k，Tand|·|k，Tare the restriction of||·||kand|·|kon triangle or tetrahedron T∈Th.

§2.　Existence and Uniqueness of the Solution of Continuous Problem

Theorem 1There exists an unique solution（u，p）∈H×Q，such that（2.1）holds.

Proof We know，（1.1）and（2.1）are equivalent when p∈H1（Ω）.So the solution of（1.1）is the solution of（2.1），we only need to prove that（2.1）has an unique solution.By coercivity（1.3），we know a（·，·）is positive definite.In（2.1），let F（v）=0 and replace v with u，we have

by the second equation of（2.2），we know that b（u，p）=0，i.e.，

By the regularity of equation（1.1）［7］，we know：when Ω∈Cn+2and f∈Wm，s（Ω）n，the solution of（8）（u，p）∈［Wm+2，s（Ω）∩H01（Ω）］n×［Wm+1，s（Ω）∩L02（Ω）］holds

where s and m are integers.

§3.Arbitrary Scheme of Stationary Stokes Problem Based on Bubble Functions

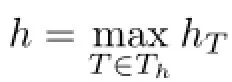
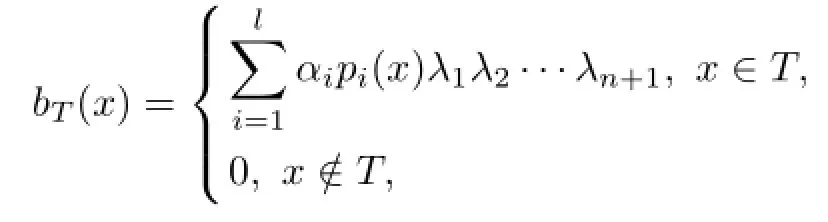
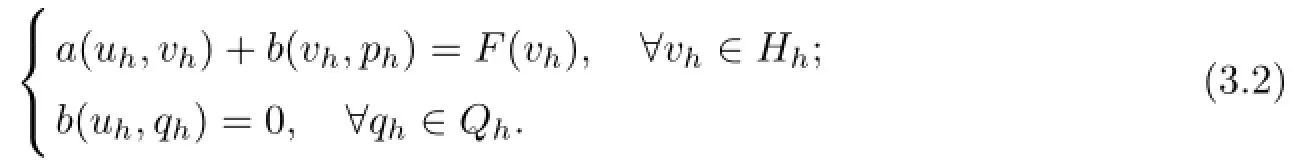
For problem（3.2），As we all know，to prove the discrete B-B condition holding is difficulty. here，we do it with Falk-Osborn’s technique proposed in［7］.

We make the following assumptions in the first place

（A1） D⊂H′×Q′，such that∀（F，G）⊂D，problem（2.1）has the unique solution（u，p）∈H×Q；

（A2）There exists a Hilbert space V，such that Q continuously embeds into V and∀d∈V′there exists（yd，λd）∈H×Q holds

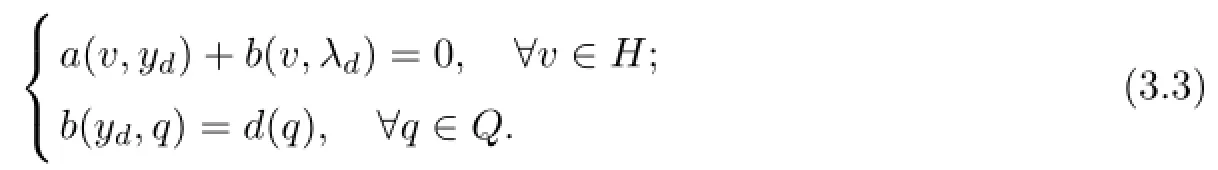
（A3）There exists W such that H embeds into W yields

where

（A4）There exists s（h）＞0，such that

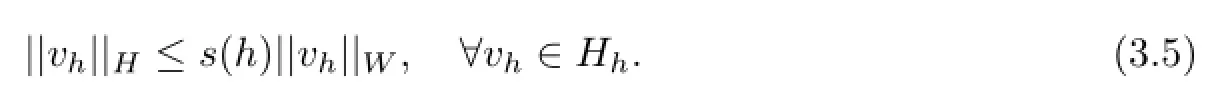
（A5）There exists an operator rh：Y→Hh，such that∀v∈Y，

where Y=｛u，yd；d∈V′｝，u is the solution of（2.1）and ydis the solution of（3.3）.

（A6）When

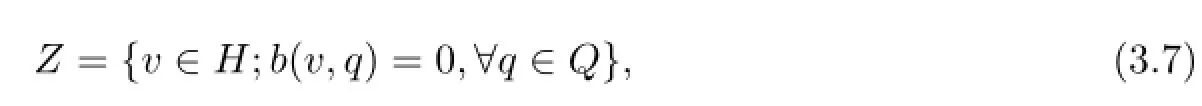
we have Zh⊂Z.

Theorem 2［7］We have the following five conclusions

（1）If（A2），（A3）and（A5）hold，then（3.2）has the unique solution（uh，ph）∈Hh×Qh.

（2）If（A1）～（A5）hold，then error estimates below are valid

∀qh∈Qh，where C＞0 is a constant.

（3）If（A1）～（A6）all hold，then error estimates are valid

where C＞0 is a constant.

（4）If（A1）～（A3）and（A5）hold，then the following error estimate is valid

（5）If（A1）～（A3），（A5）and（A6）hold，then

In order to ensure the existence and uniqueness of solution for the discrete problem（3.2），We construct an operator rh，such that the assumption（A5）which in theorem 2 is valid.

We define the operator rh：H→Hh，∀v∈H，such that

where Pkh：（H1（Ω））n→Wkhis L2-projection operator，i.e.，for all v∈（H1（Ω））n，we have

and

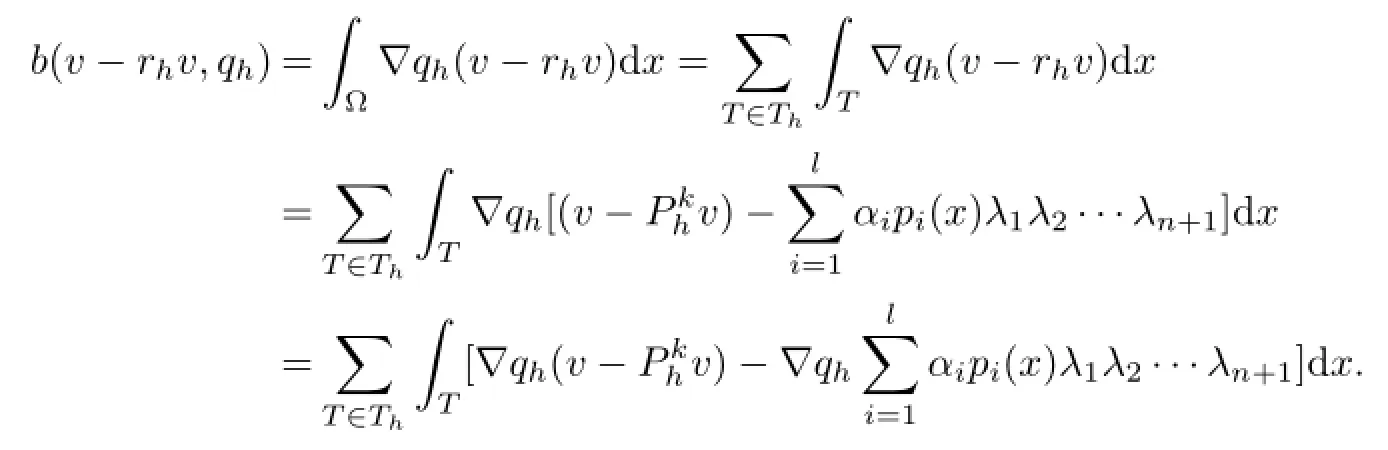
It is obvious that b（v-rhv，qh）=0 is equivalent to

Because for all▽qh∈Pk-1（T）=Pr（T），the above equation hold.To obtian αi，we take▽qhas basis function pi（x），1≤i≤l.Then we can have the next equations

Solve the equations，we have

where Cijare constants and only related to the dimension of the space.By the definition of the oprator rh，we can choose αisatisfy（3.11）.Then applying H¨older inequality，we have

Thus，by the definition of rhagain，we have

Meanwhile，we have

Then，by（3.8），（3.14）and（3.15），we conclude that H，Hhand rhsatisfy（A5）.By the conclusion（1）of Theorem 2，we know that problem（3.2）has the unique solution（uh，ph）∈Hh×Qh. Next，we estimate the errors.

Let ρh：Q∩Hk（Ω）→Qhbe the L2-projection，i.e.，∀q∈Q∩Hk（Ω）

Then by the Corollary 1.41 of［7］，we have

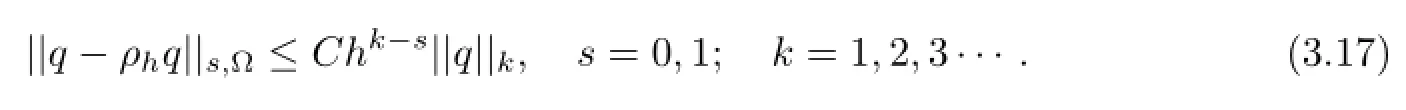
that is

We know by（A2）for all d∈L2（Ω），problem（3.3）has the solution（yd，λd）∈H×Q uniquely and has the priori estimate

For all qh，ηh∈Qh，by（4）of Theorem 2，we have

Further，we have

Substituting（3.20），（3.21）and（3.22）into（3.19），we have

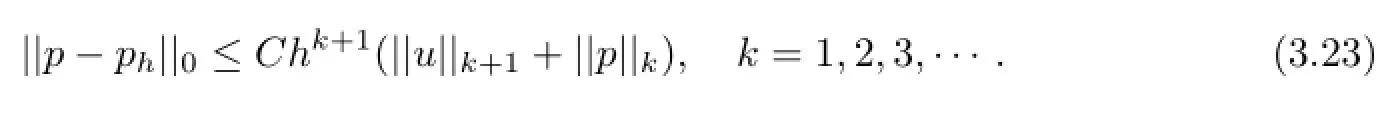
By the analysis above，we can obtain the conclusion as follows：

Theorem 3For the finite spaces Hhand Qhdefined in（3.17）and the operator rhdefined by（3.8），mixed problem（3.2）has a unique solution（uh，ph）∈Hh×Qh.When the solution of（2.1）satisfies（u，p）∈（Hk+1（Ω））n×Hk+1（Ω），we obtain the error estimates as follows：

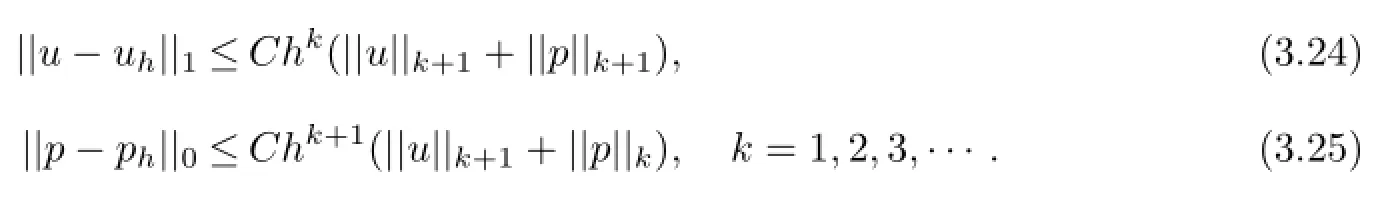
［References］

［1］BABUˇSKA I.Error-bound for finite element method［J］.Numer Math，1971，16：322-333.

［2］BREZZI F.On the existence，uniqueness and approximation of saddle-point problems arising from Lagrangian multipliers［J］.SIAM J Anal Numer，1974，13：185-197.

［3］GIRAULT V，RAVIART P A.Finite Element Methods for Navier-Stokes Equations［M］.Berlin：Springer-Vehag，1986.

［4］CROUZEIX M，RAVIART P A.Conforming and nonconforming finite element methods for solving the station Stokes equations［J］.EAIRO Math Modeling Numer Anal，1973，3：33-75.

［5］BREZZI F，FORTIN M.Mixed and Hybrid Finite Element Methods［M］.Berlin：Spring-Verlag，1991.

［6］BERNARDI C，RAUGEL G.Analysis of some mixed finite element method for the Stokes problem［J］.Math Comp，1985，44（169）：71-79.

［7］FALK R S，OSBORN J E.Error estimates for mixed methods［J］.RAIRO Numer Anal，1980，14（3）：249-277.

O241.21Document code:A

date：2016-01-02

Supported by National Natural Science Foundation of China（11371331）；Supported by the Natural Science Foundation of Education Department of Henan Province（14B110018）

Biography：CAO Ji-wei（1986-），male，native of Xiayi，Henan，Ph.D.，engages in finite element method and application.