A Remark on Persistence of Regularity for the Nonlinear Boussinesq System in Dimension Two

SU Xing，CAO Jie，ZHANG Jian-lin

（1.College of Information Science and Technology，Donghua University，Shanghai 201620，China；2.Department of Applied Mathematics，Zhongyuan University of Technology，Zhengzhou 450007，China）



A Remark on Persistence of Regularity for the Nonlinear Boussinesq System in Dimension Two

SU Xing1，CAO Jie1，ZHANG Jian-lin2

（1.College of Information Science and Technology，Donghua University，Shanghai 201620，China；2.Department of Applied Mathematics，Zhongyuan University of Technology，Zhengzhou 450007，China）

This paper investigates the Cauchy problem for the nonlinear Boussinesq system in dimension two，and prove that for any initial data（u0，θ0）in H1+s×H1+s，where s∈（0，1），the persistence of regularity holds.

the Cauchy problem；nonlinear Boussinesq system；persistence of regularity

2000 MR Subject Classification:35Q30，35Q35，76B03

Article ID:1002—0462（2016）01—0102—09

Chin.Quart.J.of Math.

2016，31（1）：102—110

§1.　Introduction

The Boussinesq equations is a system of nonlinear partial differential equations which models the thermal convection and geophysical flows，which plays an important role in the atmospheric sciences and oceanographic turbulence（see，e.g.，［20，22］）.The standard model takes the following form

where u=（u1，u2）is the velocity vector field，ui=ui（x，y，t）（i=1，2），（x，y，t）∈R×R×（0，+∞），θ（x，y，t）and P（x，y，t）denote the scalar temperature and pressure of the fluid，respectively.The constant ν≥0 is the viscosity and κ≥0 is the thermal diffusivity.The unknown function θe2is the buoyancy force.

In the past decades，there has been a lot of literature about the mathematical theory of the Boussinesq equations（1.1）.In the case when ν and κ are positive constants，Cannon and DiBenedetto［2］studied the Cauchy problem.In［17］，the global well-posedness was established（see also［21］）for this case.In contrast，in the case when ν=κ=0，the global regularity problem turns out to be extremely difficult and remains open.For this case，we only have the local existence and uniqueness results due to［3］and［4］.Recently，there are many works devoted to the study of the Boussinesq system with partial viscosity or diffusivity（i.e.，ν＞0 and κ=0 or ν=0 and κ＞0）.Actually，Chae［5］and Hou and Li［8］independently proved the global well-posedness，see also［1，7］for the global well-posedness in the critical spaces and［15，25］for the case of bounded domain.Zhao［26］generalized the case in［5］to a bounded domain with typical physical boundary conditions.Jin and Fan［13］proved a global uniform regularity in the vanishing viscosity limit in a slip boundary domain.Hu，Kukavica and Ziane［9］proved that a global in time solution exists which is locally in time bounded functions and in［10］，they proved the persistence of regularity holds.When ν and κ depend on the temperature，Lorca and Boldrini［18］proved the global existence of strong solutions for small initial data.In［19］，they obtained the global existence of weak solutions and the local existence of strong solutions for general initial data.Recently，Wang and Zhang［24］proved the global well-posedness.Sun and Zhang［23］obtained the existence of global existence of strong solutions to the initial boundary value problem.Li，Pan and Zhang［16］proved the existence of a unique global smooth solution over a smooth boundary domain.Moreover，Huang［11］addressed the well-posedness in the polygonal-like domains with Yudovich’s type data.In［12］，he proved the global well-posedness of strong solutions and existence of the global attractor.

In this paper，we are interested in the general case that the viscosity ν=ν（θ）and thermal diffusivity κ=κ（θ）depend on the temperature θ.The Boussinesq system reads

For simplicity，we assume that ν（τ）and κ（τ）are C2-functions satisfying that there exist positive constantsandsuch that，for all τ∈R，

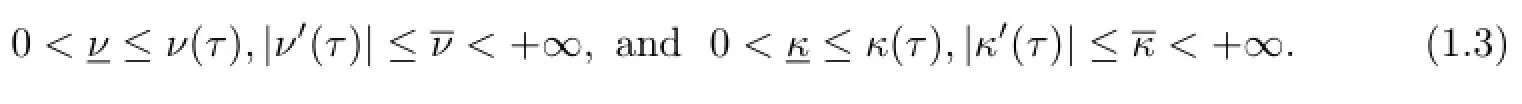
To our knowledge，the persistence of regularity for the Cauchy problem of the nonlinear Boussinesq system in dimension two were not previously considered.So，We shall study the Cauchy problem to the system（1.2）.

The rest of this paper is organized as follows.In Section 2，we state some notations and auxiliary lemmas which will be used throughout the paper and our main result.In Section 3，we complete the proof of Theorem 2.1.

§2.　Preliminaries

In this section，we state some preparations for our consideration and our main result.

Lemma 1（The Gagliardo-Nirenberg Inequality［6］）Let u∈Lq（Rn）and its derivatives of order m，Dmu∈Lr（Rn），1≤q，r≤+∞.For the derivatives Dju，0≤j＜m，the following inequality holds

Lemma 2［23］Let Ω⊂R2be any bounded domain with smooth C1boundary.Consider the 2D Stokes system with variable coefficient problem

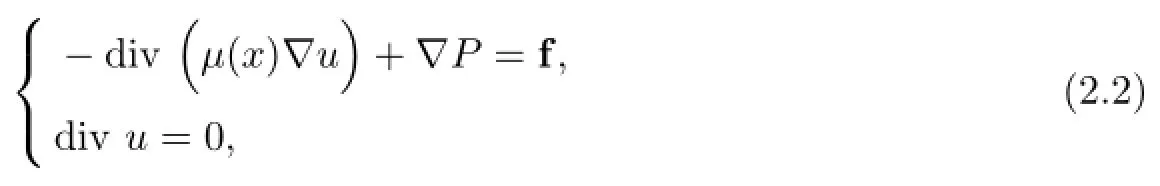
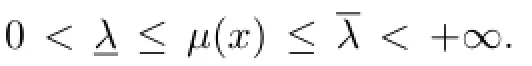
Denote by Λ=（-∆）1/2the square root of the negative Laplacian.

Now we are in a position to state our main result as follows.

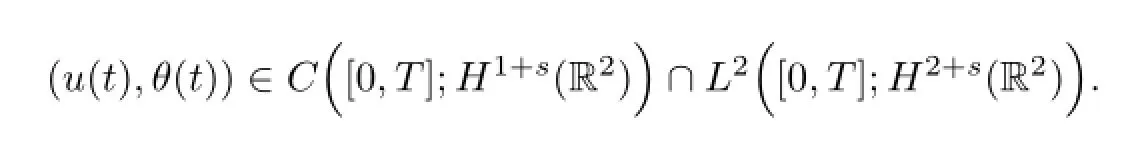
§3.　Proof of Main Results

In this section，we prove Theorem 2.1，whose proof will be done as follow，and consists of a priori estimates on an arbitrary time interval［0，T］.

Taking L2inner product of（1.2）3with θ and by（1.3），we have

Integrating（3.1）over［0，T］，we have，for all t∈［0，T］，

Multiplying（1.2）1by u and integrating the result equation by parts over Ω，we have

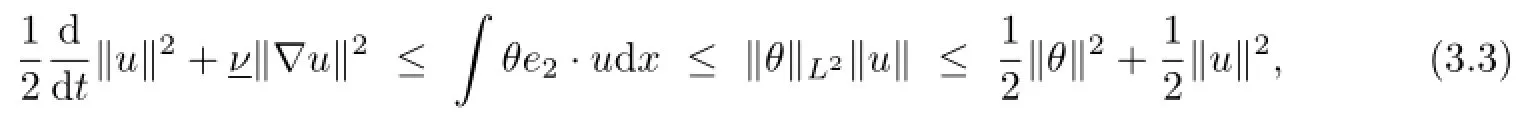
integrating over［0，T］and applying the Gronwall inequality，we can get that，for all t∈［0，T］，

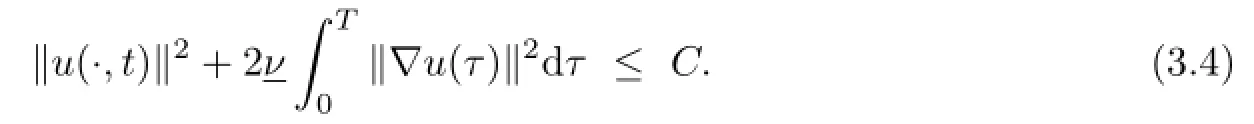
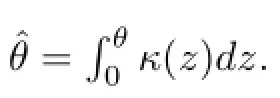
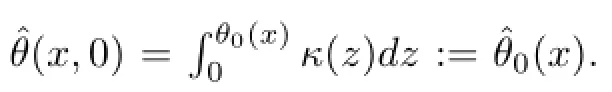
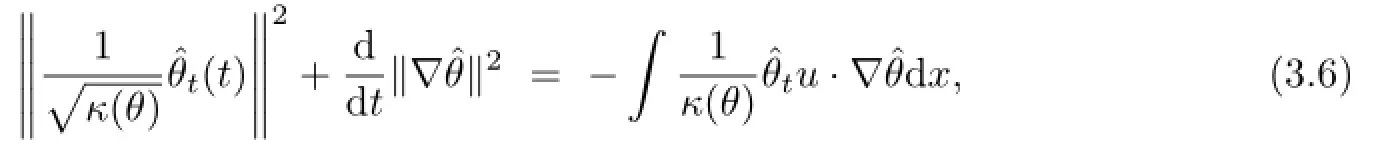
hence，

Using Lemma 2.1，the H¨older inequality and the interpolation inequality，we get for all ε＞0，

Using the elliptic estimate on（3.5）and the Young inequality，we can get

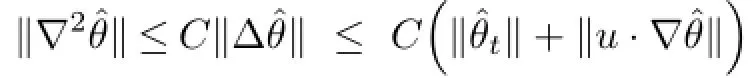
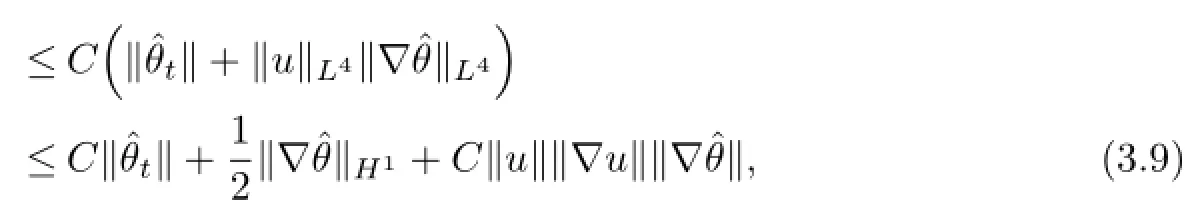
which implies that

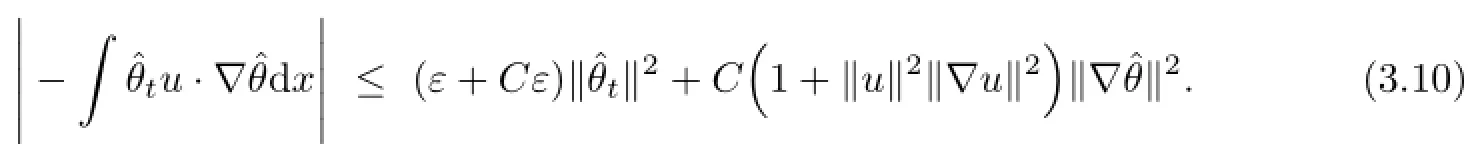
Inserting（3.9）into（3.7），and taking ε＞0 small enough，we conclude

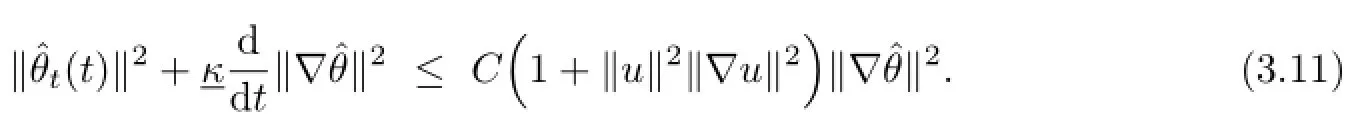
Using（3.4）and the Gronwall inequality，we get

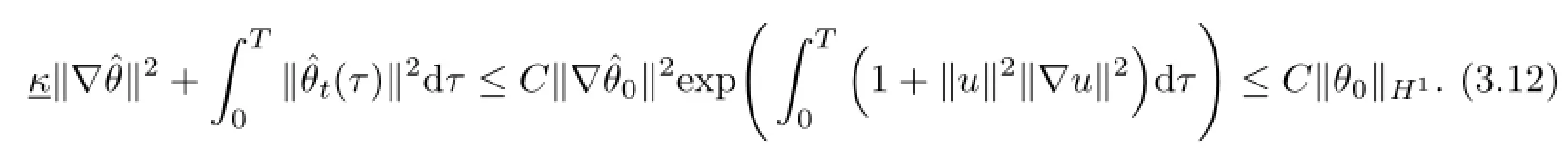
Using（3.5）once again，and by Lemma 2.1，we have

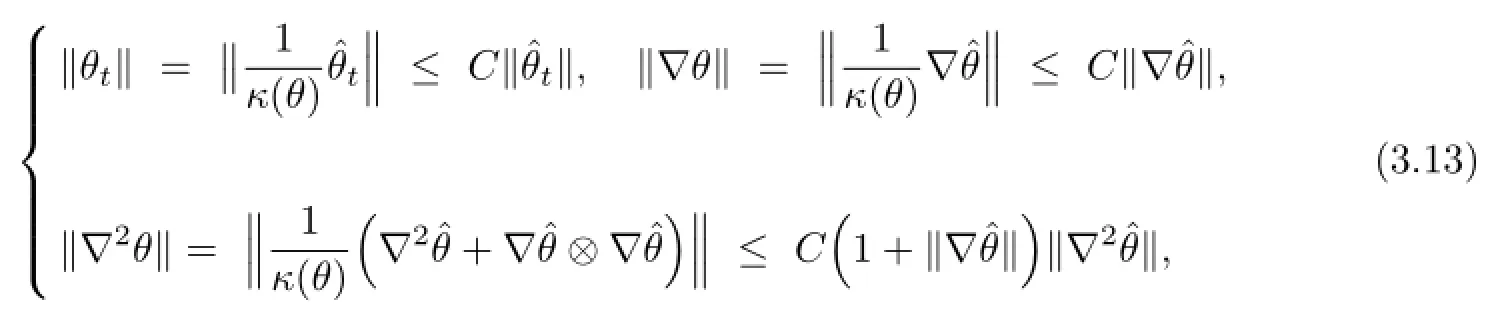
which，together with（3.12），leads to

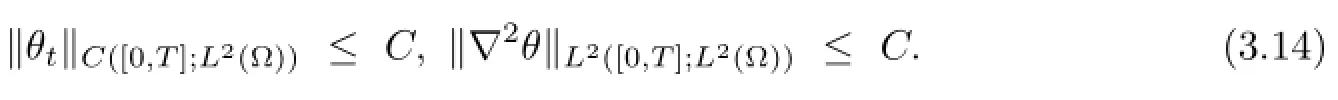
Multiplying（1.2）1by utand integrating the resulting equation by parts over Ω，we have

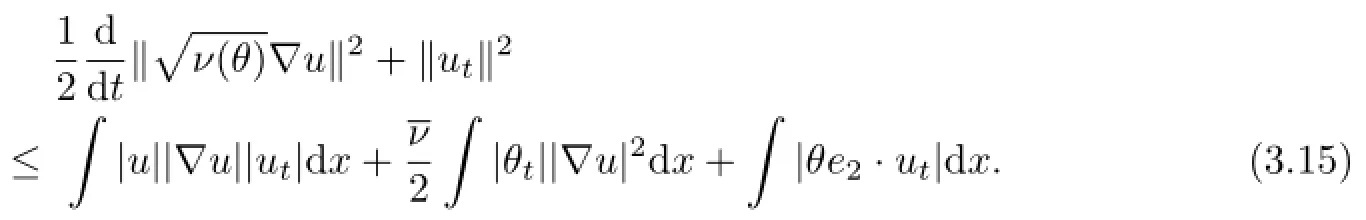
Using the H¨older inequality，the Cauchy-Schwarz inequality and Lemma 2.1，we have

which，together with（3.15），yield

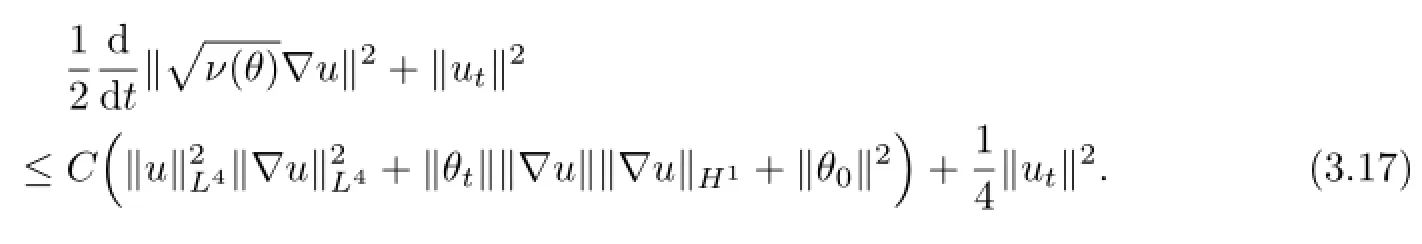
Applying the Sobolev embedding theorem，we can get，for all ε＞0，

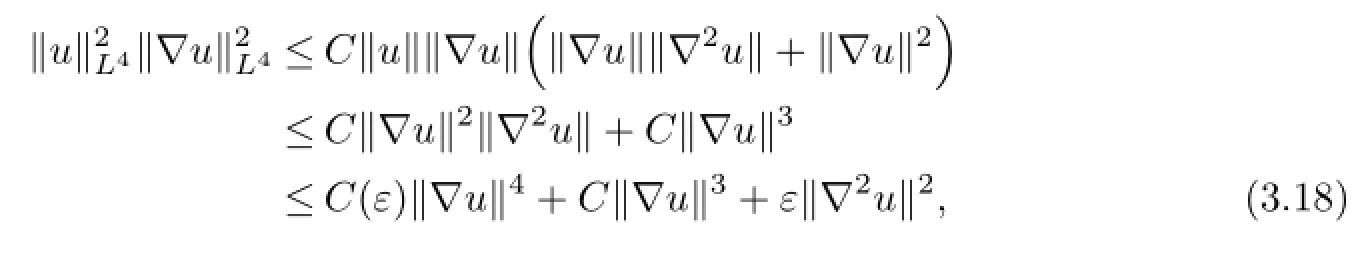
where we have used（3.4）and ε＞0 is a small number to be determined later on.So，inserting（3.18）to（3.17），we have，for any ε＞0，

By Lemma 2.2 with f=-ut-u·▽u+θe2and（3.18），we can obtain

By（3.20），we know that

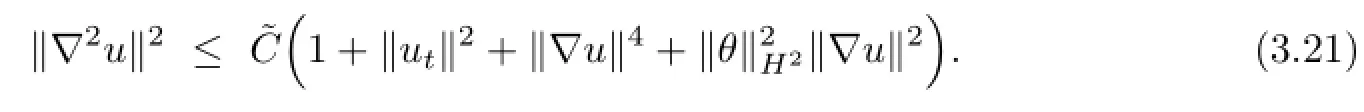
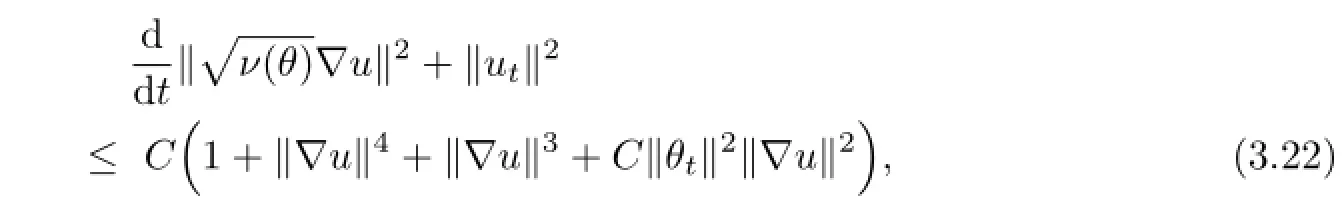
which，by（3.4），（3.14）and the Young inequality，yields

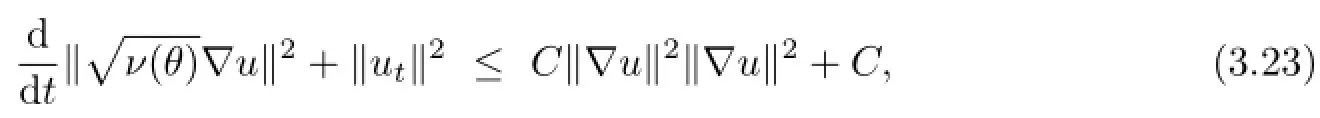
integrating over［0，T］and using by the Gronwall inequality，gives，for all t∈［0，T］，

From（3.20）and（3.13），by（3.13）and the fractional theorems and then letting p→+∞，we arrive at the key estimates

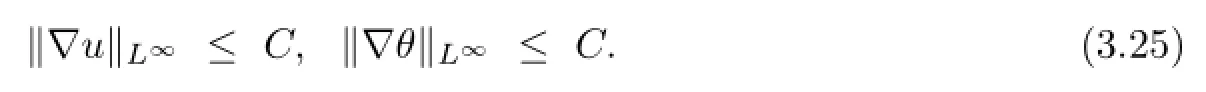
Applying the operator Λ1+sto（1.2）1and taking a scalar product of both sides with Λ1+su and then integrating it by parts，we get

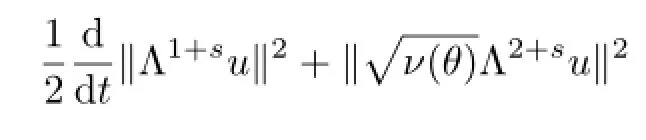
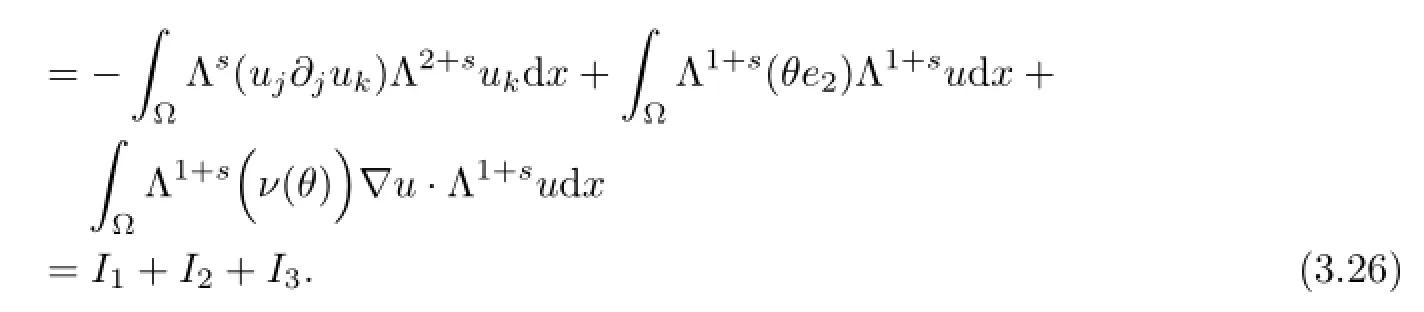
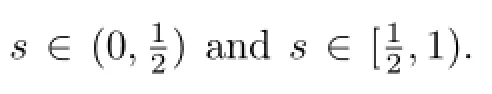
where we have used for the fractional embedding theorems

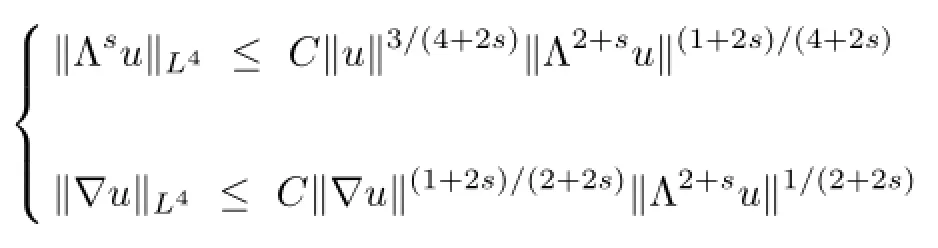
and the embedding

After applying Young’s inequality，by（3.35）and（3.36），we obtain，for all s∈（0，1），

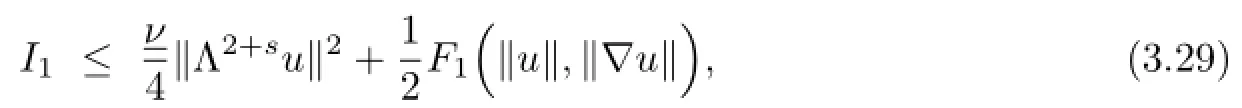
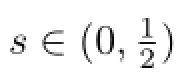
Using（3.32），we can obtain

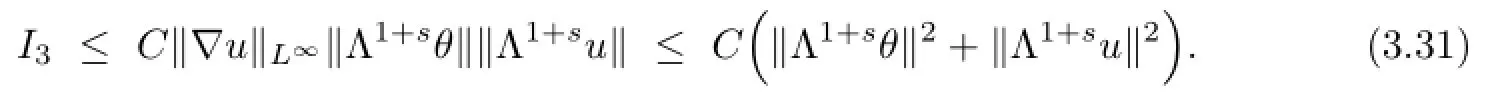
Taking Λ1+sof（1.2）3，dot multiplying the resulting equation with Λ1+sθ，after integrating it by parts，then we get

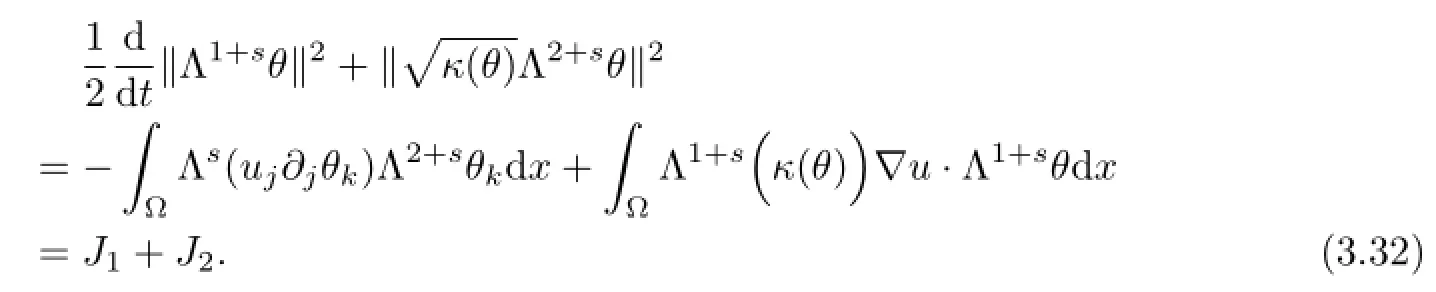
Similar argument applied to the equation of θ，we get

By（1.3）and summing up（3.26）and（3.32）and adding（3.29）～（3.31）and（3.33）to the resulting inequality，we obtain

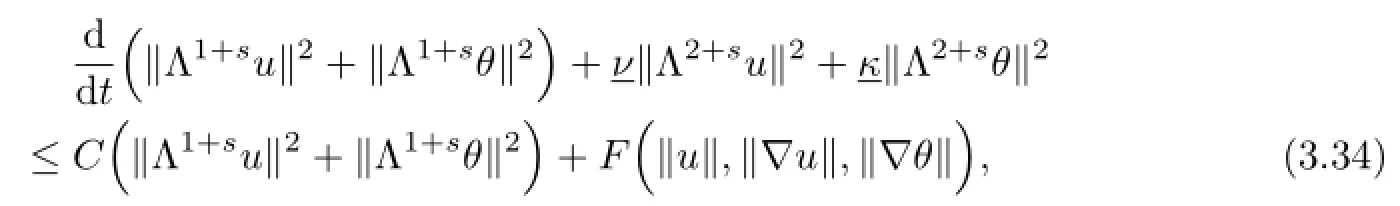
where F=F1+F2is an explicit polynomial.Using the Gronwall inequality，we find that，for all t∈［0，T］，

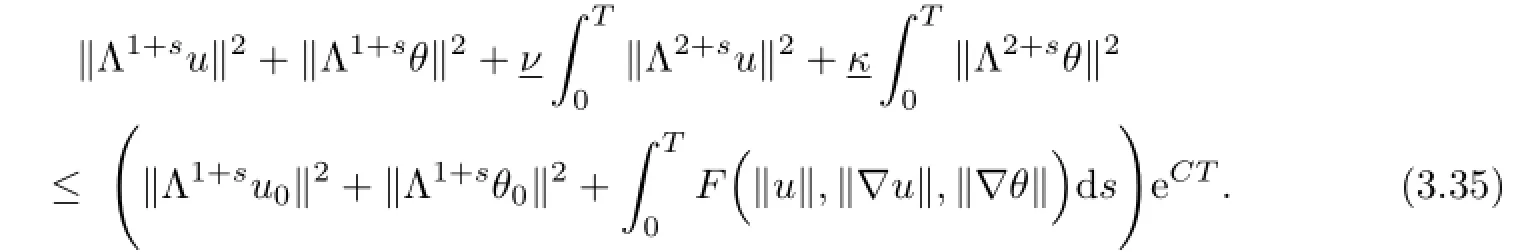
［References］

［1］ABIDI H，HMIDI T.On the global well-posedness for Boussinesq system［J］.Journal of Differential Equations，2007，233（1）：199-220.

［2］CANNON J R，DIBENEDETTO E.The initial value problem for the Boussinesq equations with data in Lp［J］.Approximation Methods for Navier-Stokes Problems，1994，300（2）：723-728.

［3］CHAE D，NAM H S.Local existence and blow-up criterion for the Boussinesq equations［J］.Proceedings of the Royal Society of Edinburgh（Section A Mathematics），1997，127：935-946.

［4］CHAE D，KIM S K，NAM H S.Local existence and blow-up criterion of H¨older continuous solutions of the Boussinesq equations［J］.Nagoya Mathematical Journal，1999，155：55-80.

［5］CHAE D.Global regularity for the 2D Boussinesq equations with partial viscosity terms［J］.Advances in Mathematics，2006，203（2）：497-513.

［6］GAGLIARDO E.Propriet`a di alcune classi di funzioni in pi`u variabili［J］.Ricerche Di Matematica，1958，7：102-137.

［7］HMIDI T.On the global well-posedness of the Boussinesq system with zero viscosity［J］.Indiana University Mathematics Journal，2009，58（4）：1591-1618.

［8］THOMAS Y HOU，LI Cong-ming.Global well-posedness of the viscous Boussinesq equations［J］.Discrete Continuous Dynamical Systems，2004，12A（1）：1-12.

［9］HU Wei-wei，KUKAVICA I，ZIANE M.On the regularity for the Boussinesq equations in a bounded domain［J］.Journal of Mathematical Physics，2013，54（8）：1-10.

［10］HU Wei-wei，KUKAVICA I，ZIANE M.Persistence of regularity for the viscous Boussinesq equations with zero diffusivity［J］.Asymptotic Analysis，2015，91（2）：111-124.

［11］HUANG Ai-min.The 2D Euler-Boussinesq equations in planar polygonal domains with Yudovich’s type data［J］.Communications in Mathematics Statistics，2015，2（3-4）：369-391.

［12］HUANG Ai-min.The global well-posedness and global attractor for the solutions to the 2D Boussinesq system with variable viscosity and thermal diffusivity［J］.Nonlinear Analysis：Theory，Methods and Applications，2015，113：401-429.

［13］JIN Liang-bing，FAN Ji-shan.Uniform regularity for the 2D Boussinesq system with a slip boundary condition［J］.Journal of Mathematical Analysis Applications，2013，400（1）：96-99.

［14］KATO T，PONCE G.Commutator estimates and the Euler and Navier-Stokes equations［J］.Communications on Pure Applied Mathematics，1988，41（7）：891-907.

［15］LAI Ming-jun，PAN Rong-hua，ZHAO Kun.Initial boundary value problem for two-dimensional viscous Boussinesq equations［J］.Archive for Rational Mechanics Analysis，2011，199（3）：739-760.

［16］LI Hua-peng，PAN Rong-hua，ZHANG Wei-zhe.Initial boundary value problem for 2D Boussinesq equations with temperature-dependent heat diffusion［J］.Journal of Hyperbolic Differential Equations，2015，12（3）：469-488.

［17］LI Yan-guang.Global regularity for the viscous Boussinesq equations［J］.Mathematical Methods in the Applied Sciences，2004，27（3）：363-369.

［18］LORCA S A，BOLDRINI J L.The initial value problem for a generalized Boussinesq model：regularity and global existence of strong solutions［J］.Mat Contemp，1996，11：71-94.

［19］LORCA S A，BOLDRINI J L.The initial value problem for a generalized Boussinesq model［J］.Nonlinear Analysis：Theory，Methods and Applications，1999，36（4）：457-480.

［20］MCGREGOR J A.Introduction to PDEs and Waves in Atmosphere and Ocean［J］.Journal of Clinical Ultrasound，2003，6（2）：125-126.

［21］MORIMOTO H.Nonstationary Boussinesq equations［J］.Journal of the Faculty Science the University of Tokyo（Section IA，Mathematics），1992，39（1）：61-75.

［22］PEDLOSKY J，ROBERTSON J S.Geophysical fluid dynamics by Joseph pedlosky［J］.Journal of the Acoustical Society of America，1988，83（3）：1207-1207.

［23］SUN Yong-zhong，ZHANG Zhi-fei.Global regularity for the initial-boundary value problem of the 2D Boussinesq system with variable viscosity and thermal diffusivity［J］.Journal of Differential Equations，2013，255（6）：1069-1085.

［24］WANG Chao，ZHANG Zhi-fei.Global well-posedness for the 2D Boussinesq system with the temperaturedependent viscosity and thermal diffusivity［J］.Advances in Mathematics，2011，228（1）：43-62.

［25］XU Fu-yi，YUAN Jia.On the global well-posedness for the 2D Euler-Boussinesq system［J］.Nonlinear Analysis：real World Applications，2014，17（6）：137-146.

［26］ZHAO Kun.2D inviscid heat conductive Boussinesq equations on a bounded domain［J］.Michigan Mathematical Journal，2010，59：329-352.

O175.29Document code:A

date：2015-11-11

Supported by the National Natural Science Foundation of China（11271066）；Supported by the Innovation Program of Shanghai Municipal Education Commission（13ZZ048）；Supported by the the Science Foundation of Hebei Province（A2013410007）；Supported by the Fundamental Research Funds for the Central Universities（SUSF-DH-D-2015085）

Biography：SU Xing（1984-），male，native of Xingtai，Hebei，a Ph.D.candidate of Donghua University，engages in nonlinear evolution equations and infinite-dimensional dynamical systems.