Analysis of an Implicit Finite Difference Scheme for Time Fractional Diffusion Equation

MA Yan

（College of Technology and Engineering，Lanzhou University of Technology，Lanzhou 730050，China）



Analysis of an Implicit Finite Difference Scheme for Time Fractional Diffusion Equation

MA Yan

（College of Technology and Engineering，Lanzhou University of Technology，Lanzhou 730050，China）

Time fractional diffusion equation is usually used to describe the problems involving non-Markovian random walks.This kind of equation is obtained from the standard diffusion equation by replacing the first-order time derivative with a fractional derivative of order α∈（0，1）.In this paper，an implicit finite difference scheme for solving the time fractional diffusion equation with source term is presented and analyzed，where the fractional derivative is described in the Caputo sense.Stability and convergence of this scheme are rigorously established by a Fourier analysis.And using numerical experiments illustrates the accuracy and effectiveness of the scheme mentioned in this paper.

time fractional diffusion equation；finite difference approximation；implicit scheme；stability；convergence；effectiveness

2000 MR Subject Classification:65M06

Article ID:1002—0462（2016）01—0069—13

Chin.Quart.J.of Math.

2016，31（1）：69—81

§1.　Introduction

As an extension of the classical integer order differential equation，fractional differential equation is a kind of equation which is formed by changing integer order derivatives in a standard differential equation into fractional order derivatives.It provides a valuable tool for describing materials with memory and hereditary properties as well as non-locality and dynamic transmission process of anomalous diffusion［1］.Because researching fractional differential equation has important scientific significance and great application prospect，so finding some effective methods to solve it is an actual and important problem.Various ways to solve fractional differential equation analytically have been proposed［2］，including Green function method，Laplaceand Fourier transform method，but most of fractional differential equations cannot be solved analytically.Therefore，to develop numerical methods for solving fractional differential equation seems to be necessary and important.Scholars have put forward many effective numerical methods：such as finite difference method，finite element method，random walk approach，spectral method，the decomposition method，the homotopy perturbation method，the integral equation method，reproducing kernel method，the variational iteration method and so many others［3］.In this paper，we will use finite difference method to examine the numerical solution of one kind of important fractional differential equation method time fractional diffusion equation.The diffusion equation describes the spread of particles from a region of higher concentration to a region of lower concentration due to collisions of the molecules and Brownian motion.While time fractional diffusion equation is a generalization of the classical diffusion equation，which is obtained from the standard diffusion equation by replacing the first-order time derivative with a fractional derivative of order α，with 0＜α＜1.It can be used to treat sub-diffusive flow process，in which the net motion of the particles happens more slowly than Brownian motion［4］.

Consider the following time fractional diffusion equation with source term

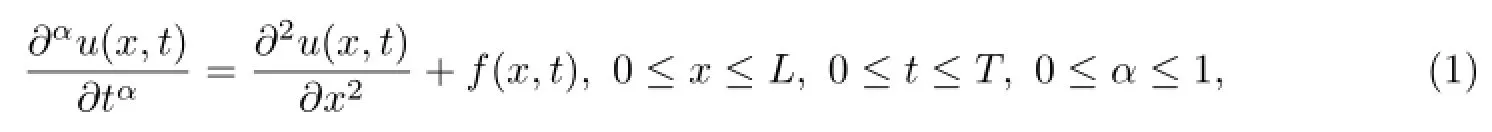
with initial condition

and Dirichlet boundary conditions

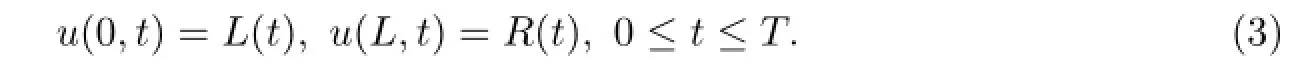
（With L（0）=g（0）and R（0）=g（L）for consistency）.

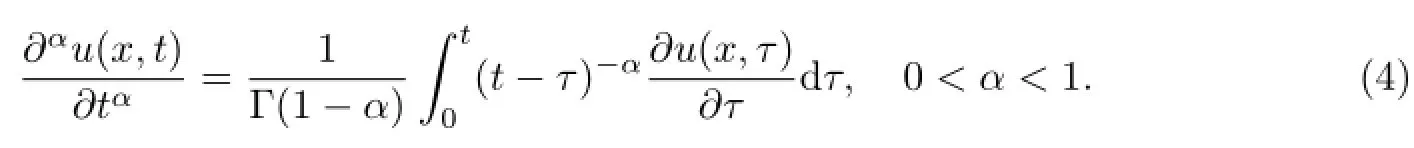
In view of the research objective of this paper，we investigate the current research status of time fractional diffusion equation.We mainly focus on the discretization technique of time fractional derivative and proof method for stability and convergence.Karatay et al［6］proposed a method for solving inhomogeneous nonlocal fractional diffusion equation，in which time fractional derivative is defined by Caputo definition.This method was based on the modified Gauss elimination method.It was proved using the matrix stability approach that the method was unconditionally stable.Lin and Xu［7］constructed and analyzed a stable and high order scheme to efficiently solve the same model as Karatay et al［6］，but with the standard initial condition. The proposed method was based on a finite difference scheme in time and Legendre spectral methods in space.Wei et al［8］presented and analyzed an implicit scheme，which is based on a finite difference method in time and local discontinuous Galerkin methods in space.Al-Shibaniet al［9］discussed a numerical scheme based on Keller box method for one dimensional time fractional diffusion equation.The fractional derivative term was replaced by the Grnwald-Letnikov formula.Unconditional stability was shown by means of the Von Neumann method.Gao et al［3］considered fractional anomalous sub-diffusion equations on an unbounded domain.This paper’main contribution lies in the reduction of fractional differential equations on an unbounded domain by using artificial boundary conditions and construction of the corresponding finite difference scheme with the help of method of order reduction.The stability and convergence of the scheme were proved using the discrete energy method.

In this paper，we will try to use a discretization formula to estimate time fractional derivative，which is cited from paper Lin and Xu［7］.For the second-order space derivative in this equation，we will adopt the classical central difference approximation.Then using the basic algebra knowledge to derive an implicit finite difference scheme，which is effective for solving our problem.For this scheme，compared with paper［7］，we adopt the same formula to discretize time fractional derivative，but for estimating space derivative，Lin and Xu［7］used Legendre spectral methods，while we will use central difference approximation.During stability and convergence analysis，we will adopt Fourier method based on mathematical induction to give the proof according to our own case and try to work out the properties about the coefficients of the scheme，which will play an important role in proof.At last，we will conduct numerical experiments to support the theoretical conclusions.

The structure of this article is as follows：in section 2，we describe the formulation of an implicit finite difference scheme for solving time fractional diffusion equation with source term. In section 3，theoretical proof for stability and convergence of this scheme are given by Fourier analysis method.In section 4，a numerical example with exact solution is provided to show the effectiveness and accuracy of the scheme.

§2.　Construction of Finite Difference Scheme for Time Fractional Diffusion Equation

In this part，we will discuss a finite difference approximation according to the following ways to discretize time fractional derivative and space second order derivative in time fractional diffusion equation（1）～（3）.Firstly，

Let

Suppose that u（xi，tn）is the exact solution of equation（1）～（3）at grid pointdenotes the numerical approximation to u（xi，tn）.

The time fractional derivative of order α is discretized by using the following approximate discretization formula from Lin and Xu［7］.

For the spatial second order derivative，central difference approximation is used

Substituting（5）and（6）into equation（1）

The following finite difference scheme can be obtained

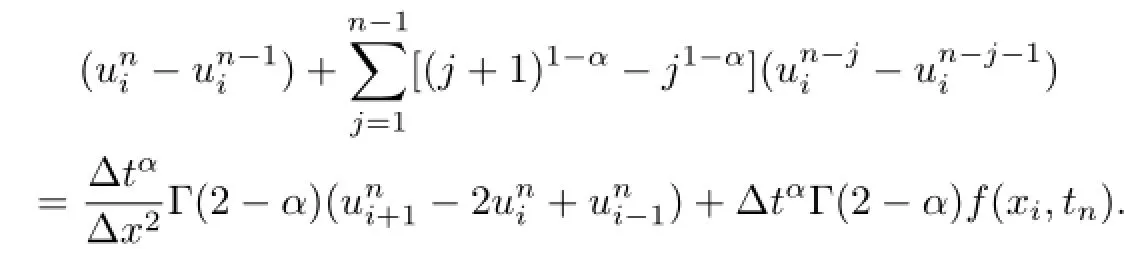
For the sake of simplification，let us introduce the notation

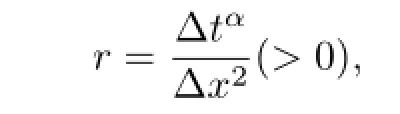
then，we can get

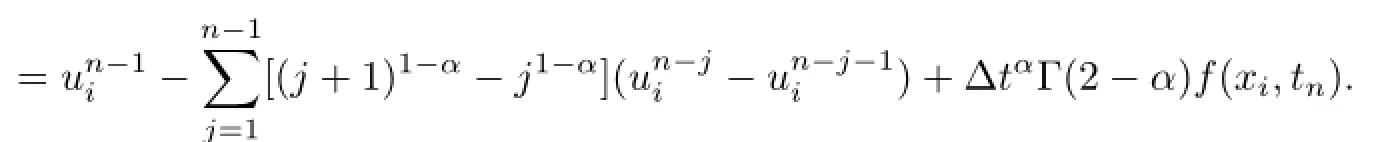
Suppose that

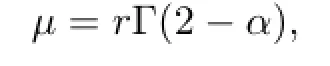
we will have

where

Further

when n=1，

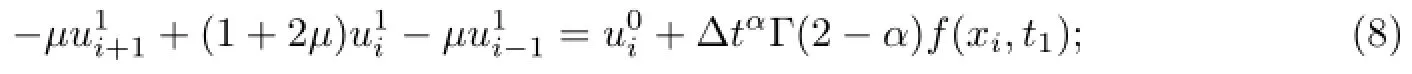
when n≥2，

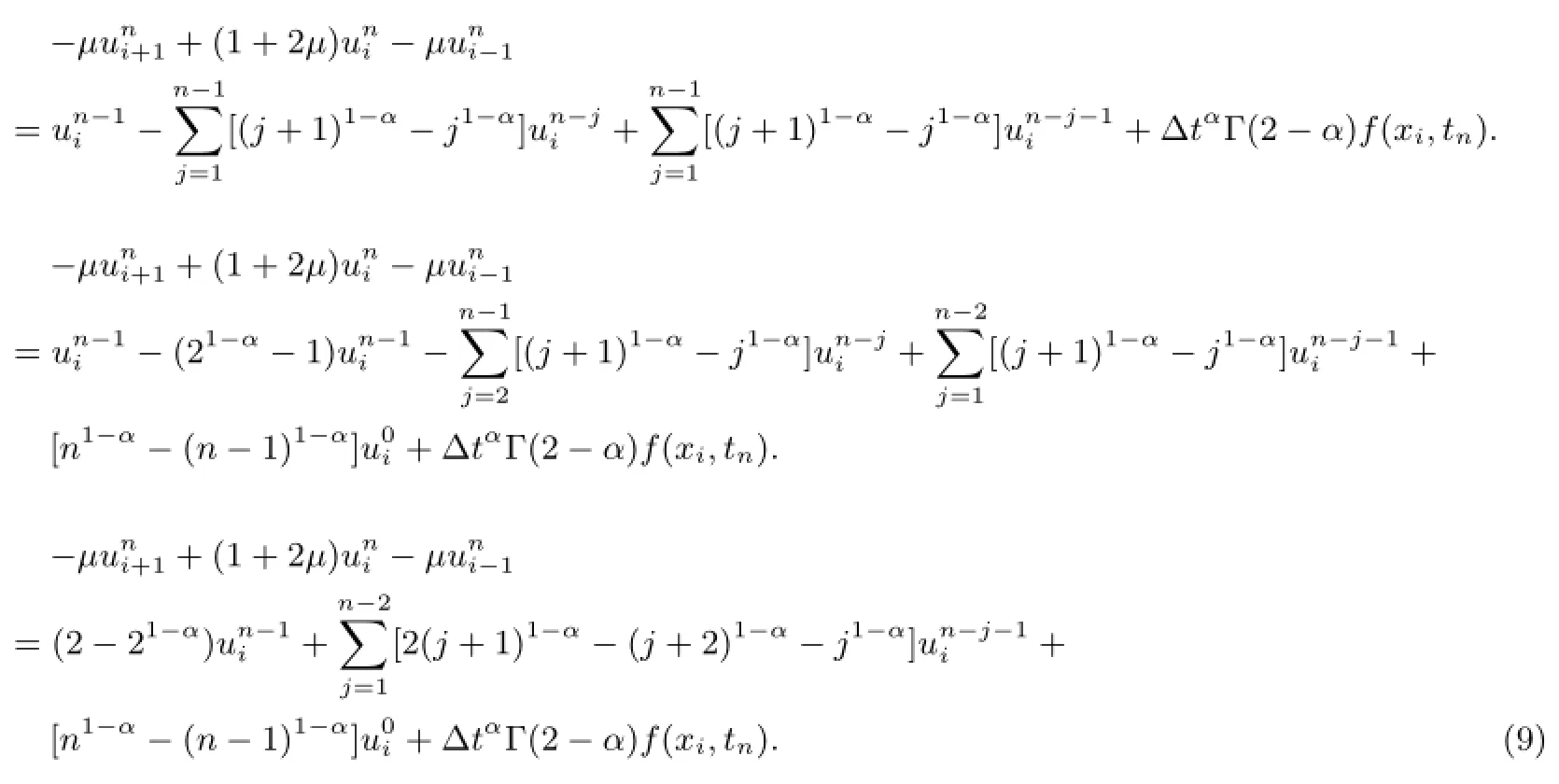
If we let

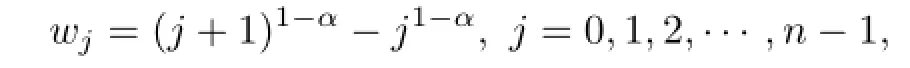
then w0=1，w1=21-α-1，so w0-w1=2-21-α，

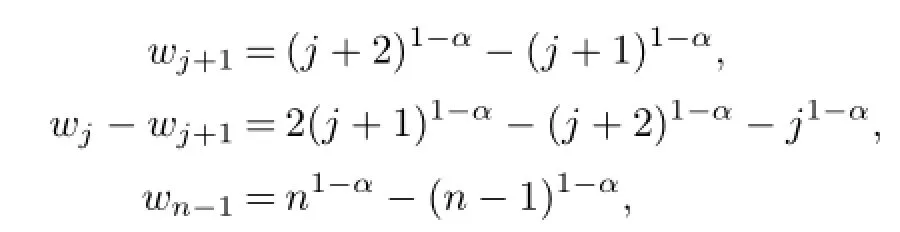
therefore，（9）becomes

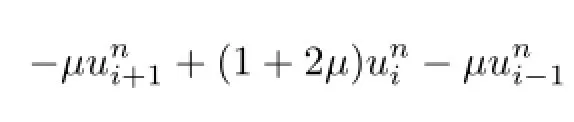
So，the implicit finite difference scheme we’ve derived to solve time fractional diffusion equation（1）～（3）can be written as follows

When n=1，

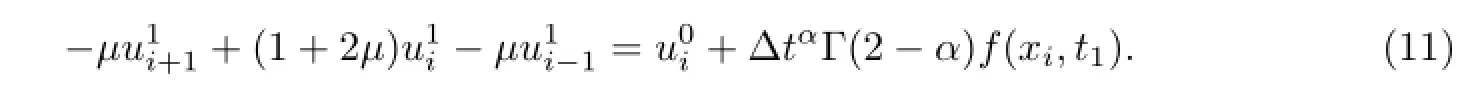
When n≥2，

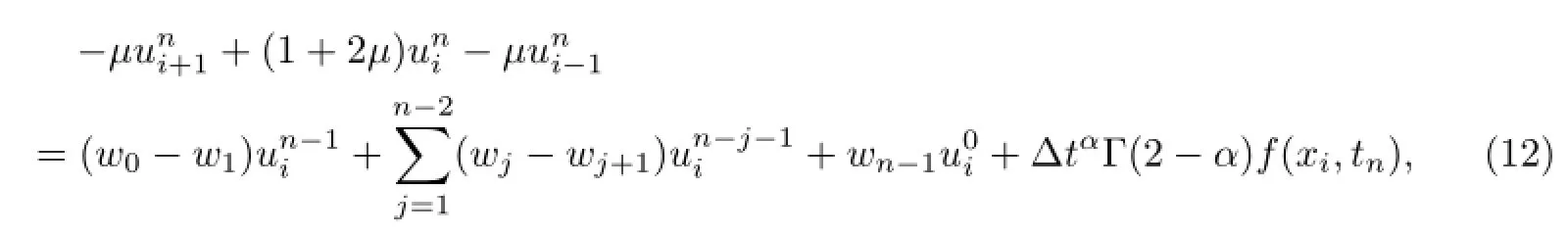
where i=1，2，···，M-1，n=2，3，···，N.

§3.　Theoretical Proof for Stability and Convergence

3.1Stability of This Finite Difference Scheme

Lemma 3.1The coefficients wj=（j+1）1-α-j1-α（j=0，1，2，···），satisfy

（1）w0=1，wj＞0，j=1，2，···；

（2）wj-wj+1＞0，j=0，1，2，···.

Proof

（1）Obviously，from wj=（j+1）1-α-j1-α，when j=0，we can get w0=1.

Since 0＜α＜1，i.e.，0＜1-α＜1，then according to the monotone increasing property of power function y=x1-αon［0，+∞），we can get（j+1）1-α＞j1-α，i.e.，（j+1）1-α-j1-α＞0 hence，wj＞0，j=1，2，···.

（2）Suppose that f（x）=（x+1）1-α-x1-α，then

so，f（x）is a monotone decreasing function on［0，+∞），thus

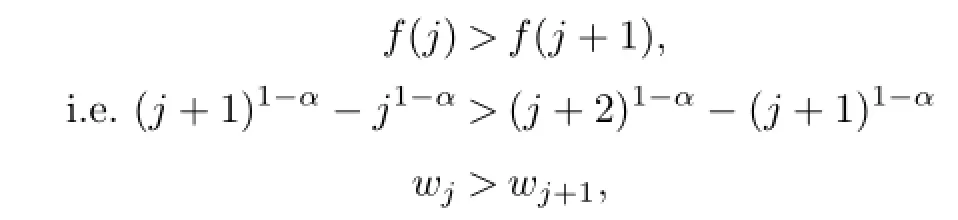
hence，wj-wj+1＞0，j=0，1，2，···.

Theorem 3.1Implicit finite difference scheme defined by（11）～（12）is unconditionally stable.

Proof Suppose that discretization of initial condition introduces the error

When n=1，

When n≥2，

Here we use Fourier analysis and apply mathematical induction to investigate the stability of this finite difference scheme.

Substitute（15）into（13）and（14），we can get

When n=1，

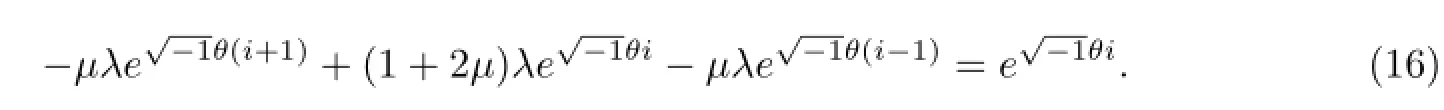
When n≥2，

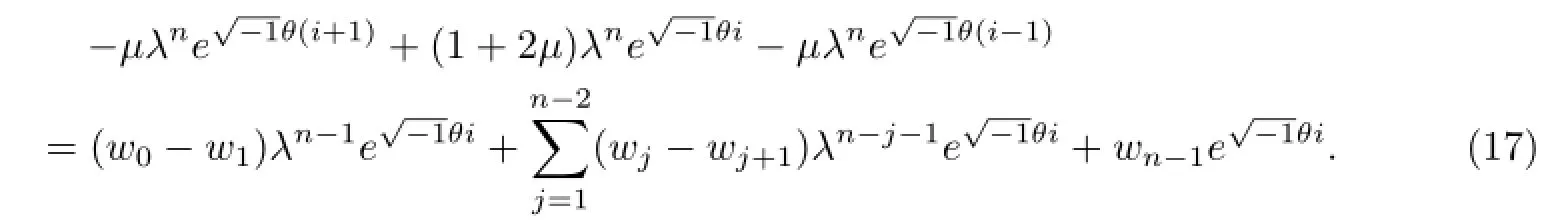
Begin with n=1，from（16），we have

obviously，

Now，suppose that

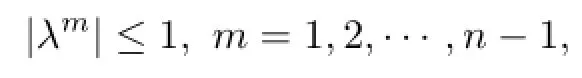
then from（17）and Lemma 3.1，

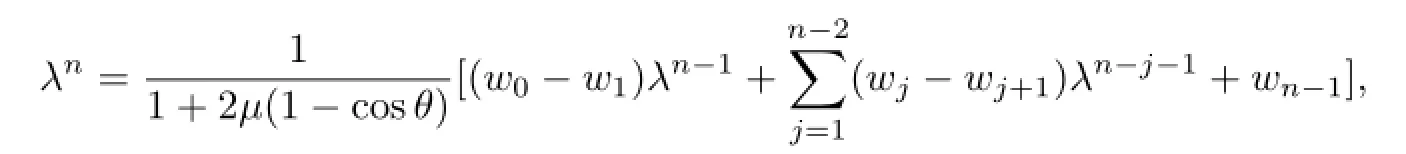
therefore，

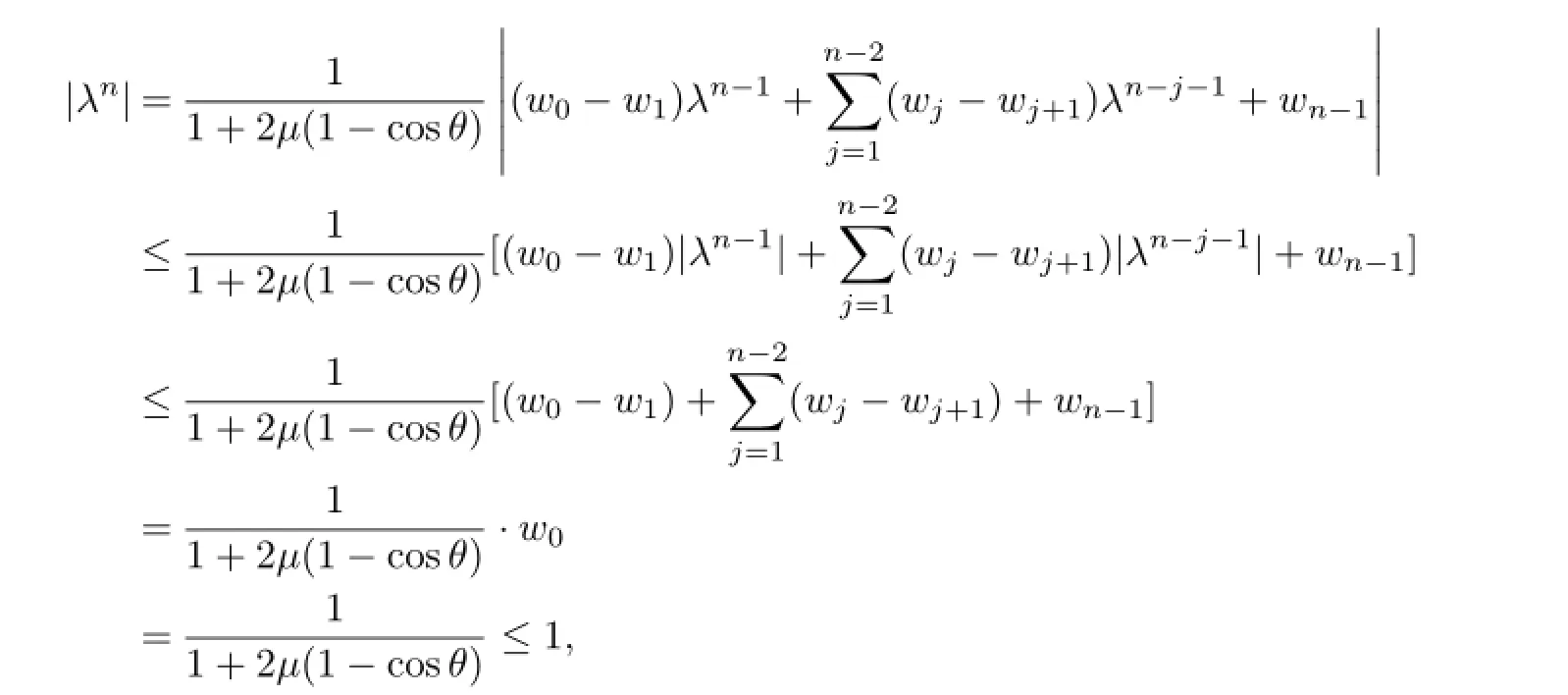
so，for all n，θ，we have|λn|≤1.

Therefore，according to the Fourier analysis’s criteria for stability，the implicit finite difference scheme defined by（11）～（12）is unconditionally stable.

3.2Convergence of This Finite Difference Scheme

In this section，we will discuss the convergence of this finite difference scheme by using Fourier analysis and following the approach of Chen et al［10］.

where

where i=1，2，···，M-1，n=1，2，···，N and we know［7］

Substituting（20），（21）into（19），we obtain

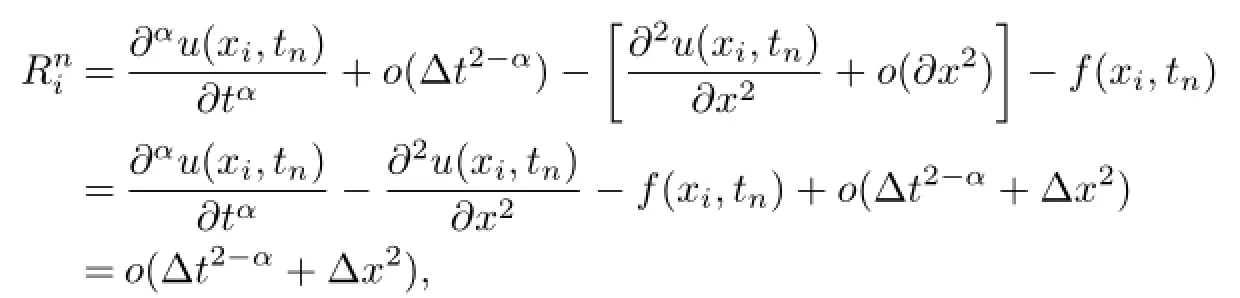
where

Consequently，there is a positive constant C（1）

i，n，such that

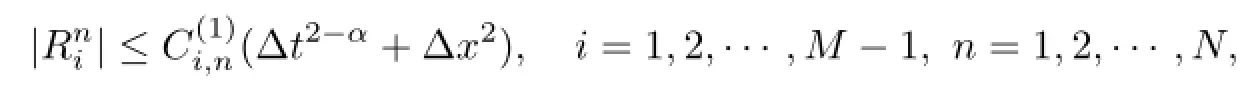
then，we have

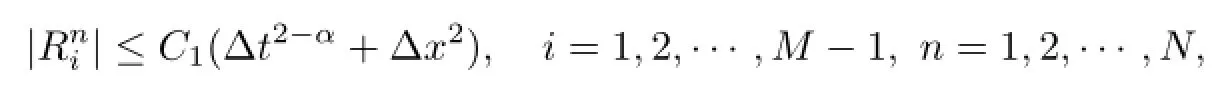
where

From（19），we have

To get the error equation，we subtract（18）from（24）and obtain

where

And the error equation satisfies the boundary conditions

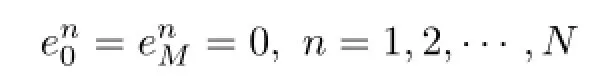
and the initial condition

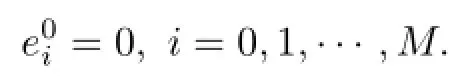
We now analyze the convergence of the scheme（18）by using Fourier analysis.

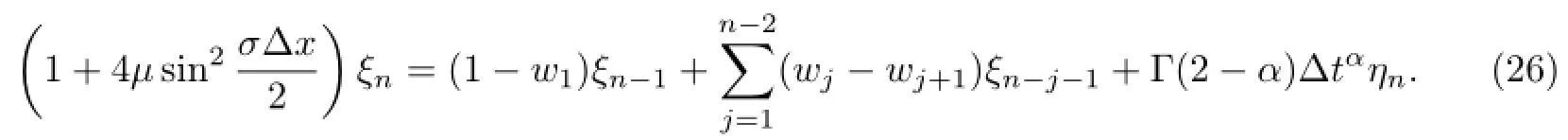
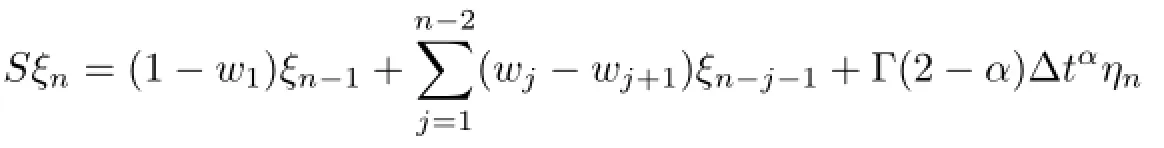
i.e.，

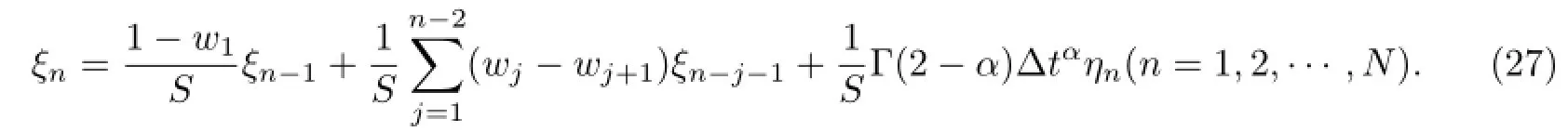
Proposition 3.1Assuming that ξn（n=1，2，···，N）is the solution of equation（27），then there exists a positive constant C2，so that|ξn|≤C2n∆tα|η1|.

we obtain

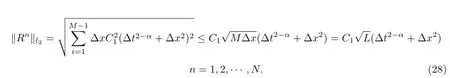
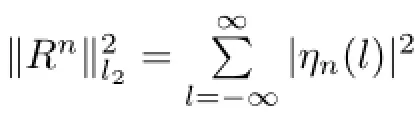
then，we have

Using mathematical induction and from

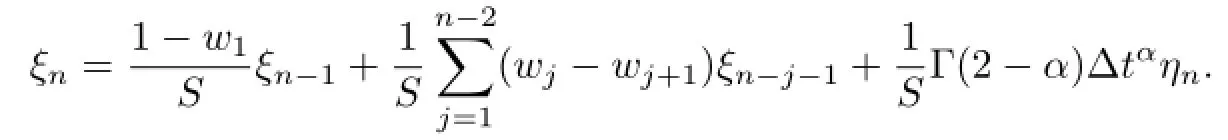
Now suppose that|ξn|≤C2n∆tα|η1|，n=1，2，···，k-1 and noticing that 0＜α＜1，S≥1 and using Lemma 3.1，we get

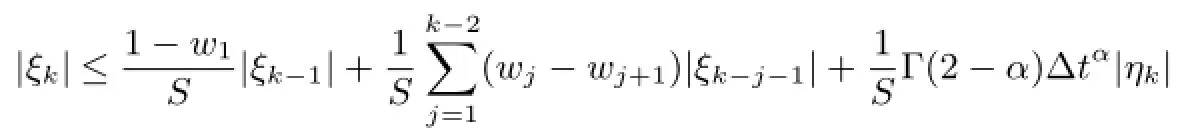
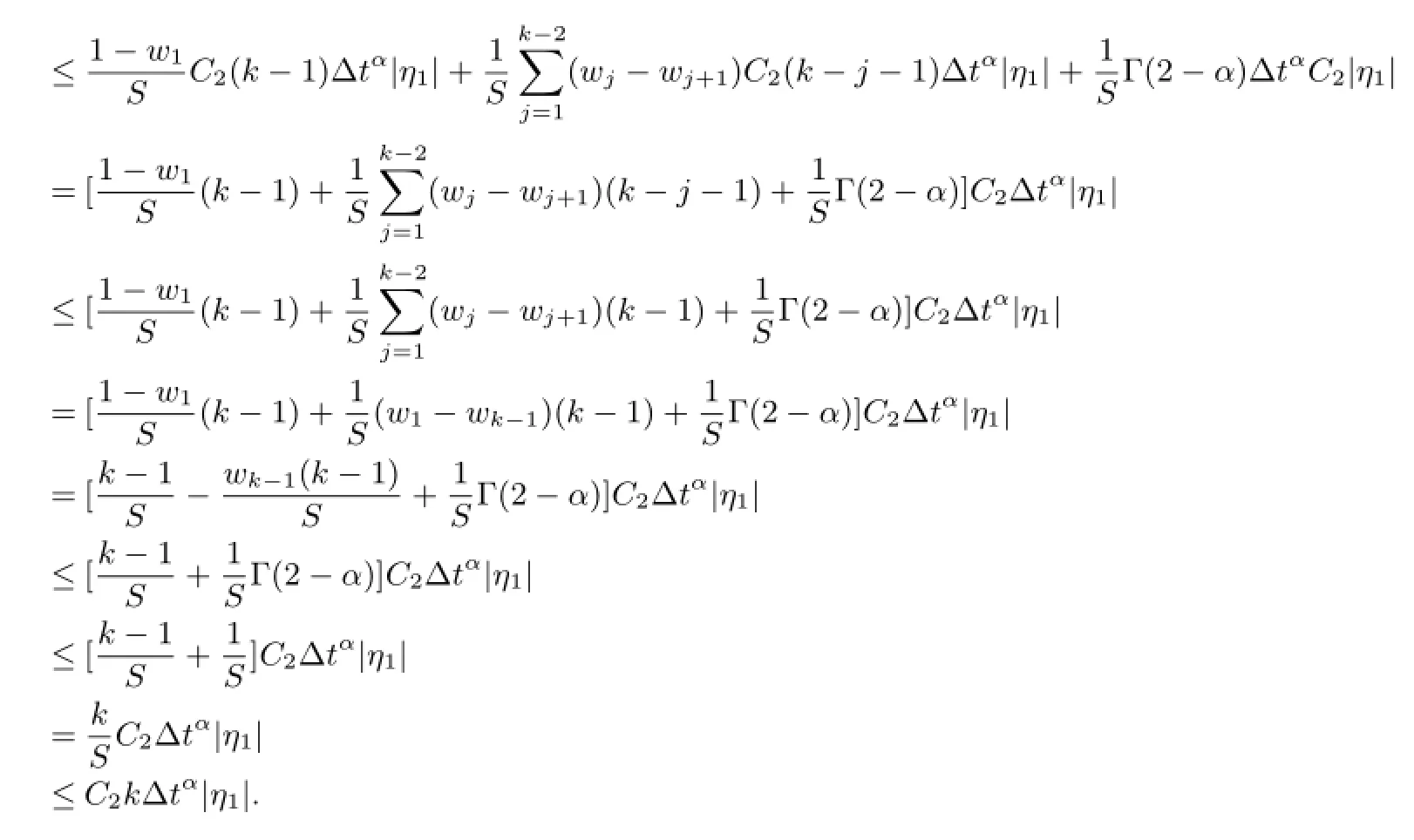
Theorem 3.2Implicit finite difference scheme defined by（11）～（12）is L2-convergent and with the convergence order o（∆t2-α+∆x2）.

We get

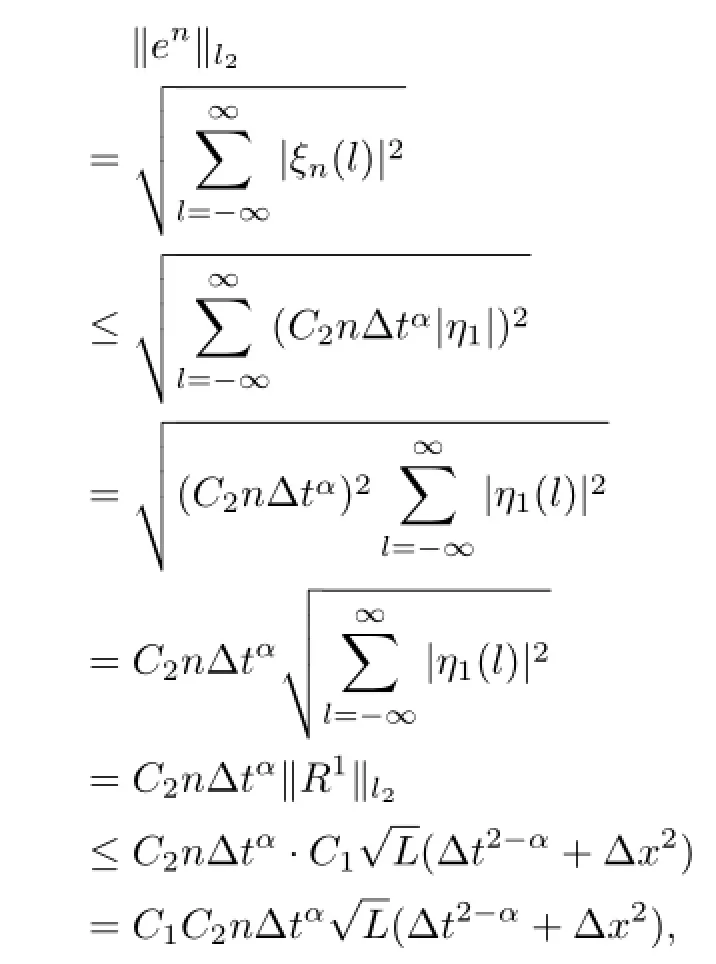
when∆t＞1，∆tα＜∆t，

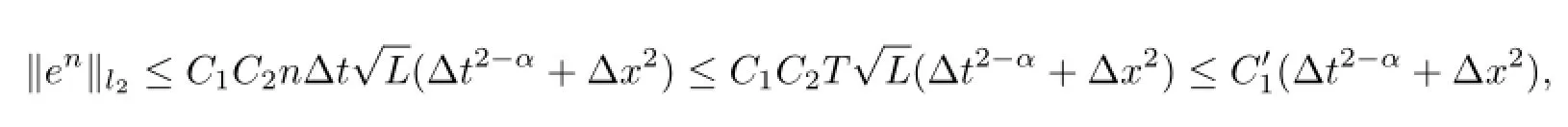
when 0＜∆t≤1，0＜∆tα≤1，

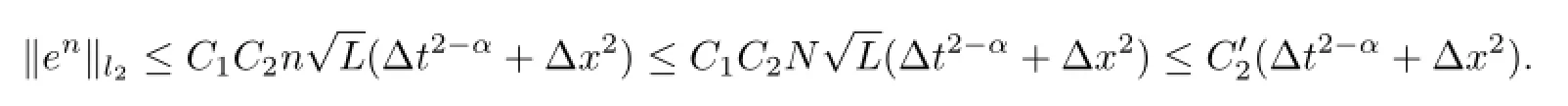
This completes the proof.

§4.　Numerical Experiments for Effectiveness

In this part，we shall illustrate several experiments to show the effectiveness of the scheme presented above.We will check the agreement behavior between numerical solution and exact solution by using fixed space step∆x and different time step∆t.

Let us consider the following time fractional diffusion equation［11］

with the initial condition

and the boundary conditions

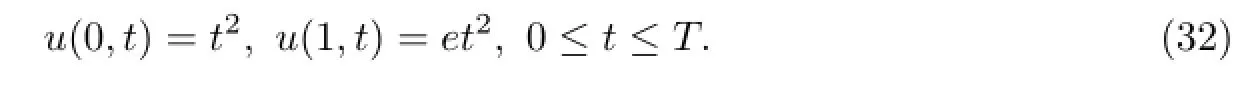
The exact solution of this fractional diffusion equation is given by

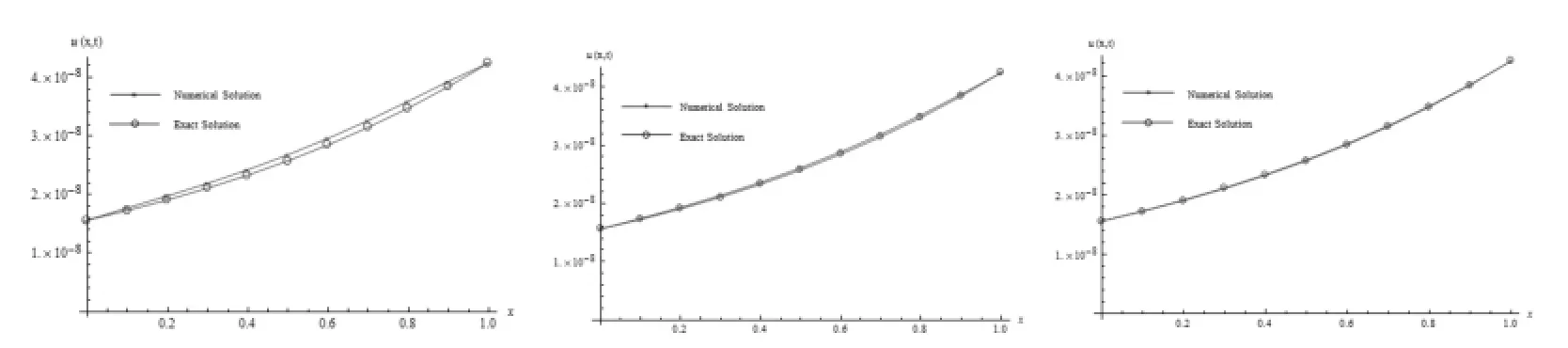
Fig.1　Comparison between Numerical Solution and Exact Solution at T=1.25×10-4（∆x= 0.1，∆t=2.5×10-5，=0.625×10-5）

From the figures above，we can see that a relatively good agreement can be achieved between numerical solution and exact solution for this particular example.This means this scheme is feasible for the case we consider.

§5.Conclusions

In this paper，we have presented one method for solving time fractional diffusion equation with source term.For the second order spatial derivative term in this equation，this method adopted central difference approximation with second order accuracy.For the time fractional derivative term，one formula was used to discretize it.This formula is derived from the definition of Caputo fractional derivative by using numerical integration method，which can achieve（1＜2-α＜2）order accuracy in time.Based on this discrete formula，one implicit finite difference scheme was derived to solve our target equation.After that，with the aid of mathematical induction，by Fourier analysis，we proved that this scheme has unconditional stability and L2-convergence with the order of o（∆t2-α+∆x2）.At last，numerical experimental work examined the effectiveness of this scheme.

［References］

［1］GAO Guang-hua，SUN Zhi-zhong.A compact finite difference scheme for the fractional sub-diffusion equations［J］.J of Computational Physics，2011，230：586-595.

［2］KILBAS A A，SRIVASTAVA H M，TRUJILLO J J.Theory and Applications of Fractional Differential Equations［M］.Netherlands：Elsevier Science and Technology，2006.

［3］GAO Guang-hua，SUN Zhi-zhong，ZHANG Ya-nan.A finite difference scheme for fractional sub-diffusion equations on an unbounded domain using artificial boundary conditions［J］.J of Computational Physics，2012，231：2865-2879.

［4］ESCHER J，GUIDOTTI P，HIEBER M，et al.Parabolic problems［M］.Basel：Springer Basel，2011.

［5］PODLUBNY I.Fractional Differential Equations［M］.San Diego：Academic Press，1999.

［6］KARATAY I，BAYRAMOGLU S R，SAHIN A.Implicit difference approximation for the time fractional heat equation with the nonlocal condition［J］.Applied Numerical Mathematics，2011，61：1281-1288.

［7］LIN Yu-min，XU Chuan-ju.Finite difference/spectral approximations for the l time-fractional diffusion equation［J］.J of Computational Physics，2007，225：1533-1552.

［8］WEI Lei-lei，HE Yin-nian，ZHANG Xin-dong，et al.Analysis of an implicit fully discrete local discontinuous Galerkin method for the time-fractional Schrodinger equation［J］.Finite Elements in Analysis and Design，2012，59：28-34.

［9］AL-SHIBANI F S，MD A I ISMAIL，ABDULLAH F A.The implicit killer box method for the one dimensional time fractional diffusion equation［J］.J of Applied Mathematics Bioinformatics，2012，2（3）：69-84.

［10］CHEN Chang-ming，LIU Fa-wang，K.Burrage.Finite difference methods and a fourier analysis for the fractional reaction-subdiffusion equation［J］.Applied Mathematics and Computation，2008，198：754-769.

［11］TAKACI D，TAKACI A，STRBOJA M.On the character of operational solutions of the time-fractional diffusion equation［J］.Nonlinear Anal，2009，72：2367-2374.

O242.2Document code:A

date：2014-03-20

Supported by the Discipline Construction and Teaching Research Fund of LUTcte（2014 0089）

Biography：MA Yan（1985-），female，native of Lanzhou，Gansu，a lecturer of Lanzhou University of Technology，M.S.D.，engages in numerical methods for partial differential equation.