The Asymptotic Limit for the 3D Boussinesq System

LI Lin-rui，WANG Ke，HONG Ming-li

（Basic Courses Department，Institute of Disaster Prevention，Sanhe 065201，China）



The Asymptotic Limit for the 3D Boussinesq System

LI Lin-rui，WANG Ke，HONG Ming-li

（Basic Courses Department，Institute of Disaster Prevention，Sanhe 065201，China）

In this paper，we show the asymptotic limit for the 3D Boussinesq system with zero viscosity limit or zero diffusivity limit.By the classical energy method，we prove that as viscosity（or diffusivity）coefficient goes to zero the solutions of the fully viscous equations converges to those of zero viscosity（or zero diffusivity）equations，which extend the previous results on the asymptotic limit under the conditions of the zero parameter（zero viscosity ν=0 or zero diffusivity η=0）in 2D case separately.

Boussinesq system；vanishing viscosity limit；vanishing diffusivity limit；energy method

2000 MR Subject Classification:35B25，35B40，35K57

Article ID:1002—0462（2016）01—0051—09

Chin.Quart.J.of Math.

2016，31（1）：51—59

§1.　Introduction

This paper is devoted to the study of the zero viscosity and zero diffusivity limit for the following so-called Boussinesq system for Rayleigh-B´ernard convection in a rotating frame

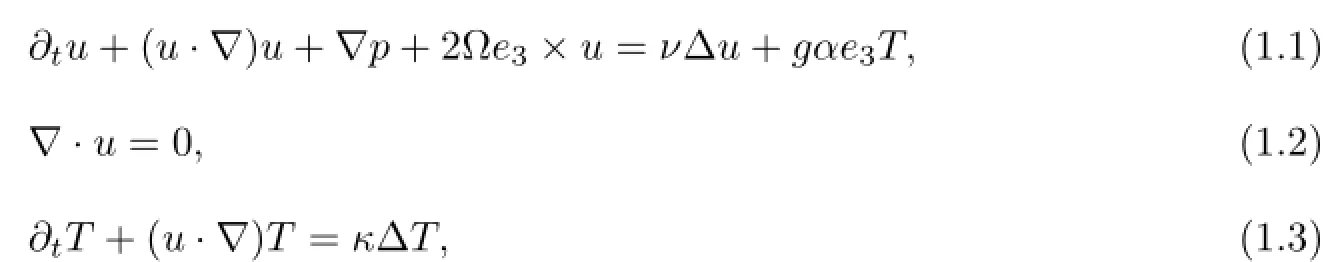
where u（x，t）=（u1，u2，u3）is the velocity vector field of the fluid，p（x，t）is the scalar pressure，Ω is the rotation rate，e3=（0，0，1）is the unit upward vector，ν≥0 is the kinematic viscosity，g is the gravity acceleration constant，α is the thermal expansion coefficient，T（x，t）is the scalar temperature field of the fluid，κ is the thermal diffusion coefficient，h is the distance between the bottom and top plates.Here we also impose the period boundary conditions in the horizontal directions for simplicity.

This system is one of the fundamental systems in fluid dynamics.It is a model for convection，i.e.，fluid motion induced by differential heating，of a layer of fluids bounded by two horizontal parallel plates a distance h apart in the Rayleigh-B´enard setting［12］with the bottom plate heated at temperature T12and the top plate cooled at the temperature T11（T11＜T12）.The Boussinesq system has important roles in the atmospheric sciences［4］.

The 2D Boussinesq equations have been the subject of many studies，the global in time regularity with ν＞ 0 is well-known［5］.Very recently，Chae［9］showed that the 2D system also has a unique smooth global in time solution with ν=0 or the η=0 and proved that as diffusivity（or viscosity）tends to zero，the solutions of the fully viscous equations converge strongly to those of zero diffusivity（or viscosity）equations.However，our results extend the previous results to 3D case for Boussinesq system on Rayleigh-B´ernard convection model.

On the other hand，we have very limited mathematical knowledge on the system，even the issue of the existence of regular enough solutions is unresolved.Indeed，the velocity equation is exactly the Navier-Stokes system（forced by a buoyancy term），whose regularity of solutions is one of the million-dollar mathematical problems of the new millennium.For the complex 3D Boussinesq system，the regularity or singularity questions of the case with ν＞0 and η=0 is also an outstanding open problem in the mathematical［12，5，10］.

Furthermore，since the Boussinesq system is very complex，many results are obtained for the nondimensional model and the infinite Prandtl number model，at the same time，fundamental mathematical issues such as the asymptotic limit on different equations have generated extensive research and many interesting result have been obtained［3，618，20］.

Formally setting κ=0 in the system（1.1）～（1.6），we can get the zero diffusivity Boussinesq system as follows

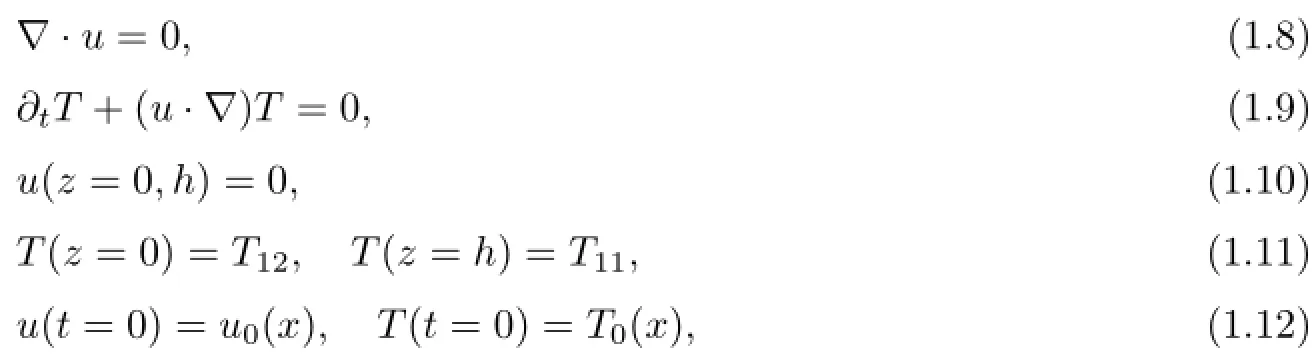
where ν＞0 is fixed.Similarly，formally setting ν=0，we can get the zero viscosity Boussinesq system：

where κ＞0 is fixed.

For the existence of the local smooth solution of the systems，see Ishimura N ea al and Fan Jin-shan and Zhou yong’s work［10，18］.

This paper is organized as follows：In section 2，we state the main results of this paper.In section 3，we prove the zero diffusivity limit.In section 4，we prove the zero viscosity limit.

§2.Main Results

In this section，we state the main results of the paper.

First，we give a common formula which will be used in this paper.

or

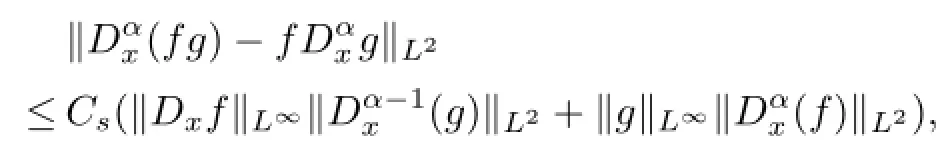
where Csis a constant.

Now we state the main results of this paper.

Theorem 1Let ν＞0 be fixed and▽·u0=0.Let s≥3 be an integer and（u0，T0）∈Hs（G），G ⊆ R3.Assume that（u，p，T）andare the local solutions of the system（1.1）～（1.6）and（1.7）～（1.12）for some time T∗＞ 0，then for any time T1∈（0，T∗），when T1＞0，（u，p，T）converge toin C（［0，T1］；Hs）as κ→0 and

Theorem 2Let κ＞0 be fixed and▽·u0=0.Let s≥3 be an integer and（u0，T0）∈Hs（G），G⊆R3.Assume that（u，p，T）andare the local solutions of the system（1.1）～（1.6）and（1.13）～（1.18）for some time T∗∗＞0，then for any time T2∈（0，T∗∗），when T2＞0，（u，p，T）converge toin C（［0，T2］；Hs）as ν→0 and

In the following，we use M to denote the constants which may differ from one line to another.

§3.　Vanishing Diffusivity Limit

with the boundary conditions

and the initial conditions

Now we start the energy estimates.

First，multiplying（3.1）by uRand integrating the resulting equation over G，by（1.8），（3.2），（3.4）and integrations by parts one gets

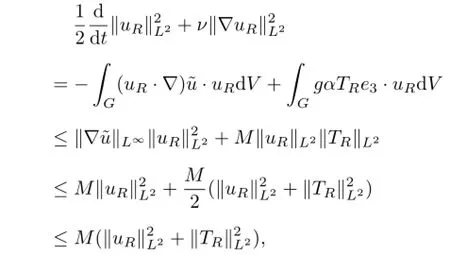
thus we get

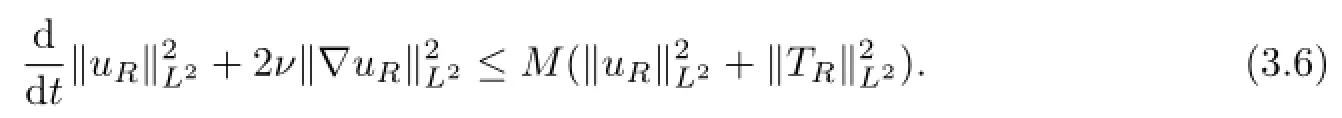
Then，multiplying（3.3）by TRand integrating the resulting equation over G，by（1.8），（3.2），（3.4）and integrations by parts，one gets

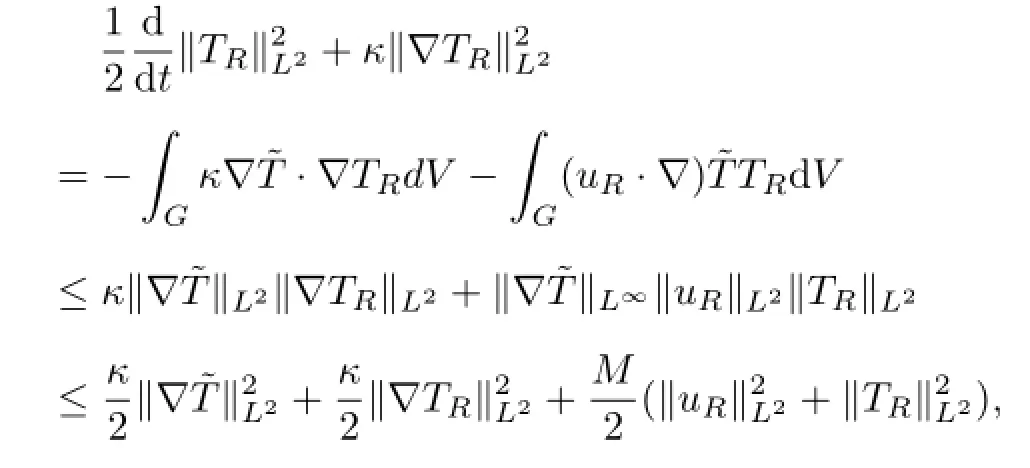
thus we get

Adding（3.6）to（3.7），one can get

then by Gronwall inequality，we have

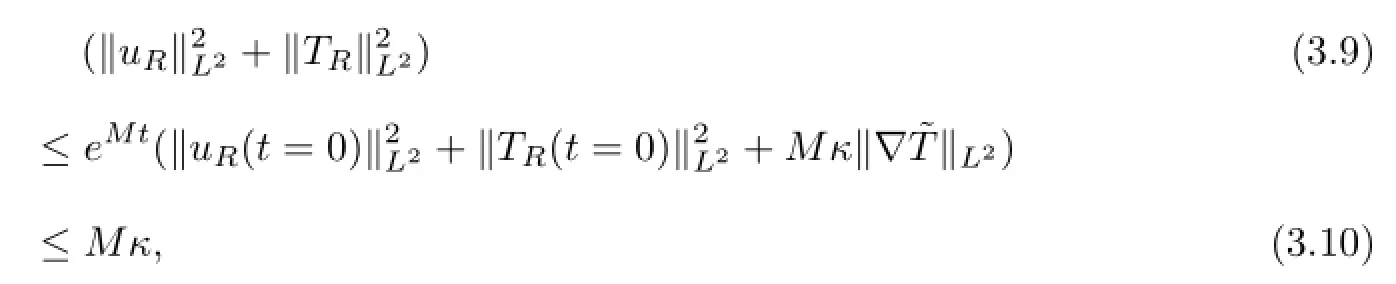
where we have used the condition（3.5）.Thus we get

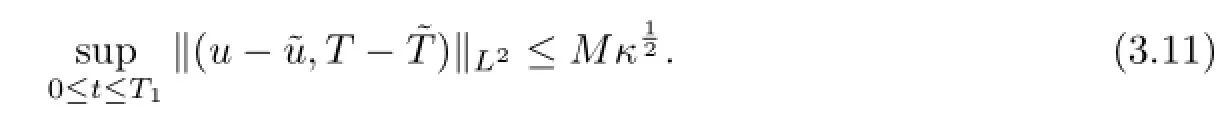
thus we get

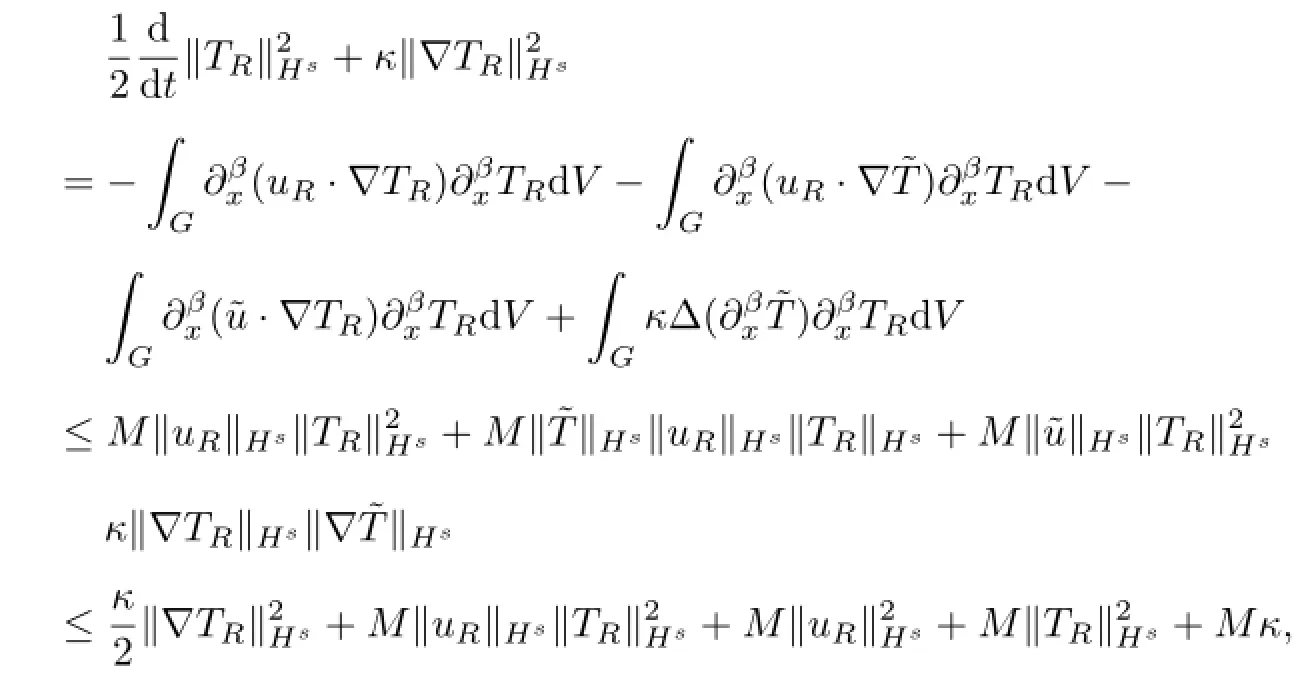
then

From（3.11）and（3.12），by Gronwall inequality we can get

This completes the proof of Theorem 1.

§4.Vanishing Viscosity Limit

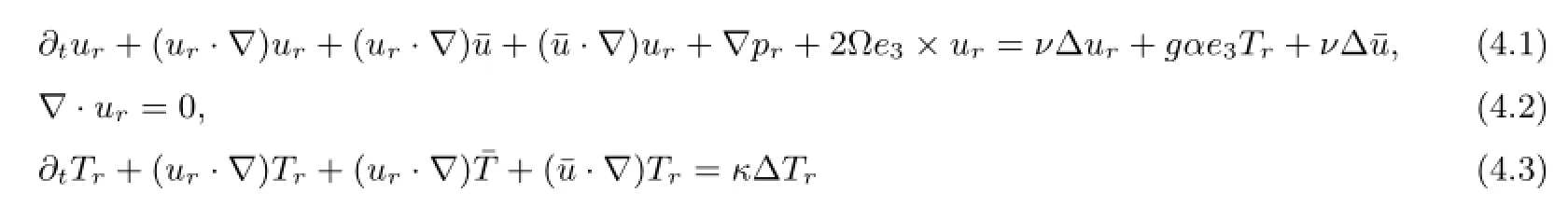
with the boundary conditions

and the initial conditions

Now we start the energy estimates.

First，multiplying（4.1）by uRand integrating the resulting equation over G，by（1.14），（4.2），（4.4），integrations by parts and Young inequality，one gets

thus we obtain

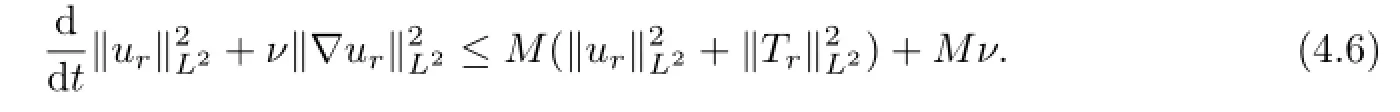
Then，multiplying（4.3）by TRand integrating the resulting equation over G，by（1.14），（4.2），（4.4）and integrations by parts，one gets

then

Combining（4.6）～（4.7）and using Gronwall inequality，we can get

where we have used the condition（4.5）.Then we get

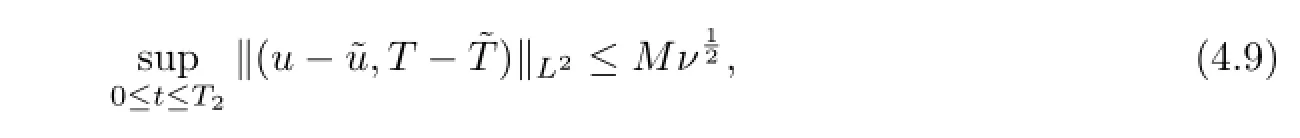
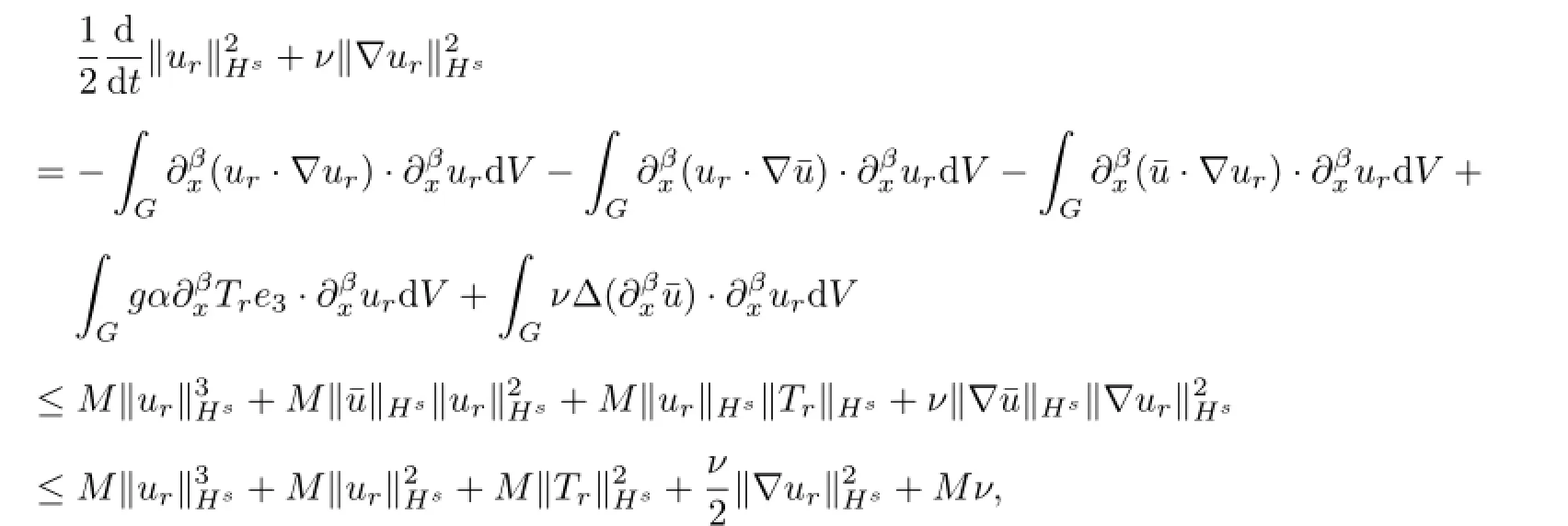
thus we get

then

From（4.10）and（4.11），by Gronwall inequality，we can get

This completes the proof of Theorem 2.

［References］

［1］GETLING A V.Rayleigh-B´enard Convection；Structures and Dynamics［M］.Singapore：World Scientific Publishing，1998.

［2］TRITTON D J.Physical Fluid Dynamics［M］.New York：Oxford University Press，1988.

［3］WANG Xiao-ming.A note on long time behavior of solutions to the Boussinesq system at large Prandtl number［J］.Contemporary Mathematics，2005，371：315-323.

［4］MAJDA A.Introduction to PDEs and Waves for the Atmosphere and Ocean［M］.AMS/CIMS：New York University，2003.

［5］CANNON J R，DiBenedetto E.The initial problem for the Boussinesq equation with data in Lp［J］.Lecture Notes in Mathematics，1980，771：129-144.

［6］SUN Zhen-ying.Global soultions and asymptotic properties for a class of partial differential equations［J］. Chinese Quarterly Journal of Mathematics，2000，15（3）：78-83.

［7］WANG Wei，WANG Shu.Semi-classical limit of cubic defocusing nonlinear Schr¨odinger system［J］.Chinese Quarterly Journal of Mathematics，2002，17（3）：18-23.

［8］LIANG Bao-song，YE Yao-jun，LI Hui-ping.On the asymptotic property of solutions to some nonlinear dissipative wave equations［J］.Chinese Quarterly Journal of Mathematics，2000，17（4）：83-86.

［9］CHAE D.Global regularity for the 2D Boussinesq equations with partial viscosity terms［J］.Adv Math，2006，203：497-513.

［10］ISHIMURA N，MORIMOTO H.Remarks on the blow up criterion for the 3D Boussinesq equations［J］.Math Models Methods Appl Sci，1999，9：1323-1332.

［11］CHAE D.Local existence and blow-up criterion for the Euler equations in the Besov spaces［J］.Asymptot Anal，2004，（38）3-4：339-358.

［12］CHAE D.On the well-posedness of the Euler equations in the Besov and Triebel-Lizorkin spaces［J］.Tosio Kato’s Method and Principle for Evolution Equations in Mathematical Physics（Sapporo，2001）.S¯urikaisekik enky¯usho K¯oky¯uroku，2001，1234：42-57.

［13］BEALE J T，KATO T，MAJDA A.Remarks on the breakdown of smooth solutions for the 3-D Euler equations［J］.Comm Math Phys，1984，94：61-66.

［14］SUN Zhen-ying.Asymptotic stability in the large of zero solution of class of partial second order nonlinear differential equation［J］.Chinese Quarterly Journal of Mathematics，2001，16（2）：13-16.

［15］KOZONO H，OGAWA T，TANIUCHI Y.The critical Sobolev inequalities in Besov spaces and regularity criterion to some semilinear evolution equations［J］.Math Z，2002，242：251-278.

［16］WANG Xiao-ming.Asymptotic behavior of the global attractors to the Boussinesq system for Rayleigh-B´enard convection at large Prandtl number［J］.Comm Pure Appl Math，2007，60（9）：1293-1318.

［17］WANG Xiao-ming.Infinite prandtl number limit of Rayleigh-B´enard convection［J］.Comm Pure Appl Math，2004，57（10）：265-1282.

［18］FAN Jin-shan，ZHOU Yong.A note on regularity criterion for the 3D Boussinesq system with partial viscosity［J］.Applied Mathematics Letters，2009，22：802-805.

［19］FRIEDMAN A.Partial Differential Equations of Parabolic Type［M］.New Tersey：Prentice-Hall，Jnc，Englewood Cliffs，NJ，1964.

［20］BODENSCHATZ E，PESCH W，AHLERS G.Recent developments in Rayleigh-B´enard convection［J］.Annual Review of Fluid Mechanics，2000，32：709-778.

O175.2Document code:A

date：2015-06-19

Supported by the Youth Science Fund for Disaster Prevention and Reduction（201207）；Supported by the Teachers’Scientific Research Fund of China Earthquake Administration（20140109）

Biographies：LI Lin-rui（1983-），female，native of Nanyang，Henan，a lecturer of Institute of Disaster Prevention，Ph.D.，engages in nonlinear partial differential equations；WANG Ke（1983-），female，native of Sanhe，Hebei，a lecturer of Institute of Disaster Prevention，engages in nonlinear partial differential equations；HONG Ming-li（1982-），female，native of Nanan，Fujian，a lecturer of Institute of Disaster Prevention，M.S.D.，engages in nonlinear partial differential equations.