两总体分布方差相等的U统计量检验方法
2016-09-22宋立新
陈 鲲,宋立新
(1.吉林师范大学教育科学学院,吉林 四平 136000;2.吉林师范大学博达学院,吉林 四平136000)
两总体分布方差相等的U统计量检验方法
陈鲲1,宋立新2
(1.吉林师范大学教育科学学院,吉林 四平 136000;2.吉林师范大学博达学院,吉林 四平136000)
利用非参数统计中的U统计量构造了检验两个总体方差是否相等的方法. 与F检验法相比,该方法不仅适用范围更加广泛,且其渐近相对效率为1.
U统计量;方差检验;渐近正态性;渐近相对效率
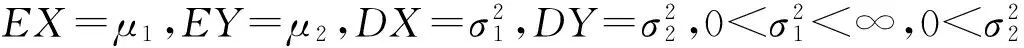
本文利用U统计量构造了解决这类问题的一种检验方法,该方法同F检验法相比,不仅适用于更加广泛的场合,而且渐近相对效率为1.
1 U统计量的建立[1]

令

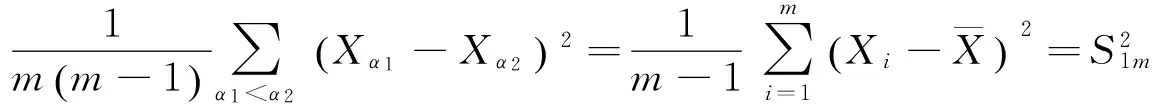
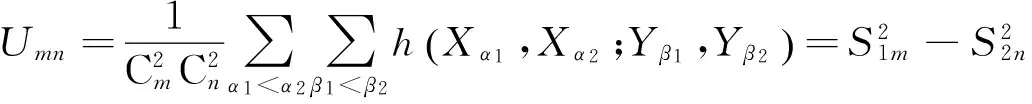
下面证明Umn是U统计量.事实上,
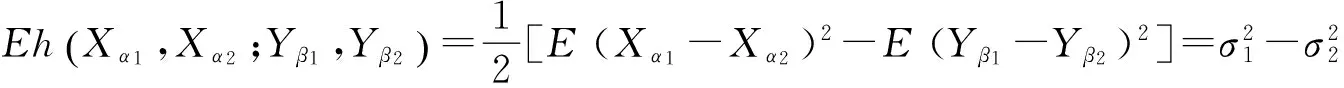
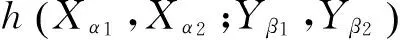
2 Umn的数学期望和方差
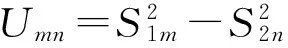

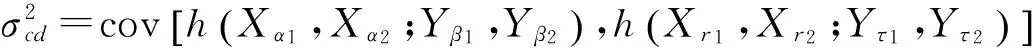

证明
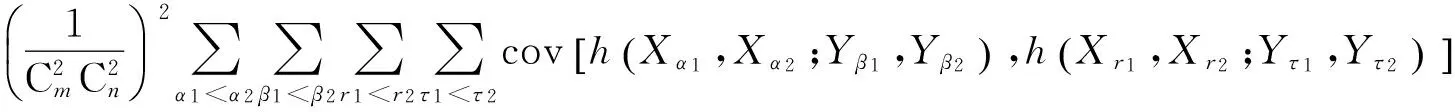
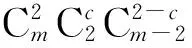
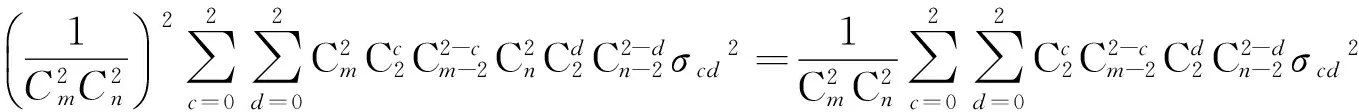

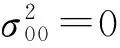
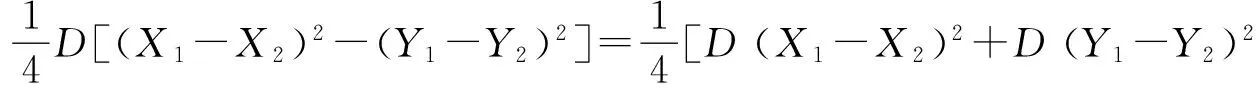
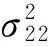
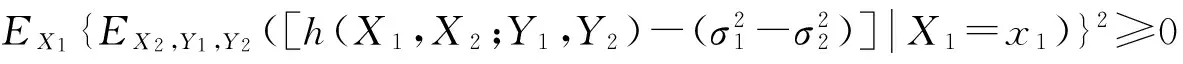
其余同理可证.
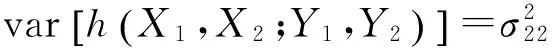
其余同理可证.
cov[(X1-X2)2,(Y3-Y4)2]+cov[(Y1-Y2)2,(Y3-Y4)2]}=
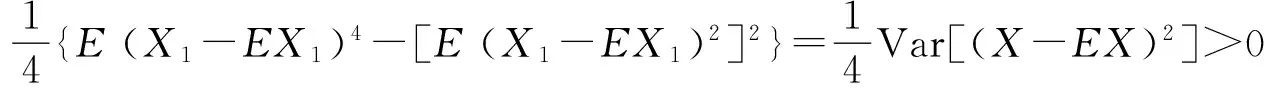
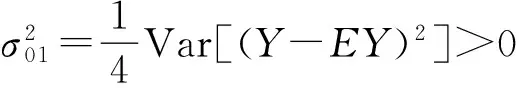
3 Umn的大样本性质
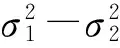


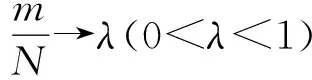

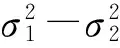
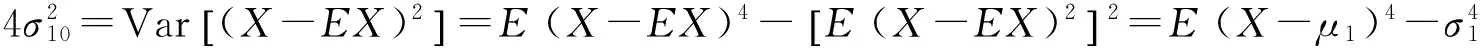

则
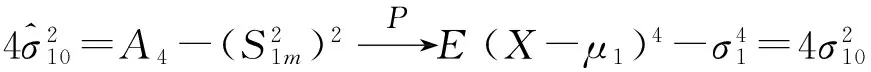
同理若令

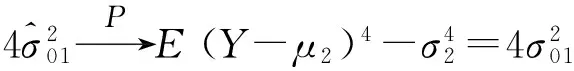
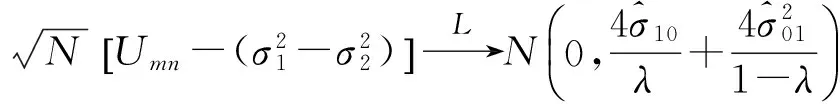
5 利用上述结果进行假设检验
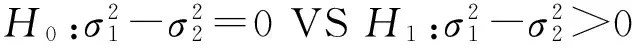
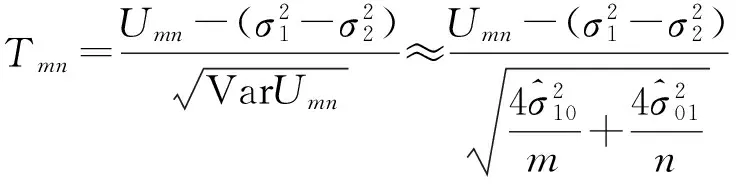
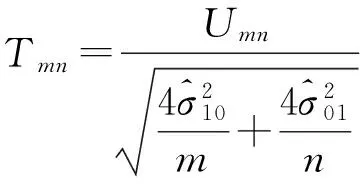
6 检验的渐近相对效率
给出了两个总体分布方差相等的U统计量检验方法,自然要研究其功效,但由于其备择假设不是简单假设,求出功效是比较困难的,这时可以同已知的这类问题的典型方法进行比较,需要求出比它们优势的Pitman渐近相对效率.[3-4]
因F检验法是最典型的两个总体分布方差相等的参数假设检验方法,所以首先和F检验法进行比较.
6.1F检验法[5]
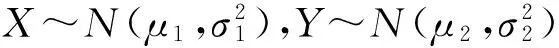
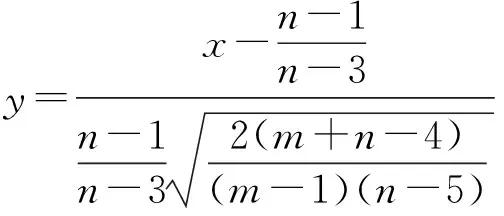
6.2比较本检验与F检验的渐近相对效率
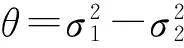
(P1)
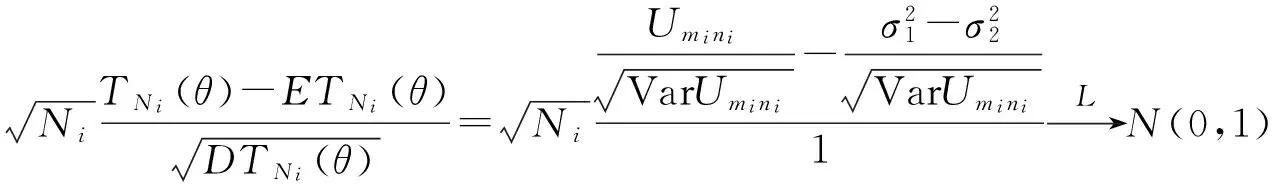
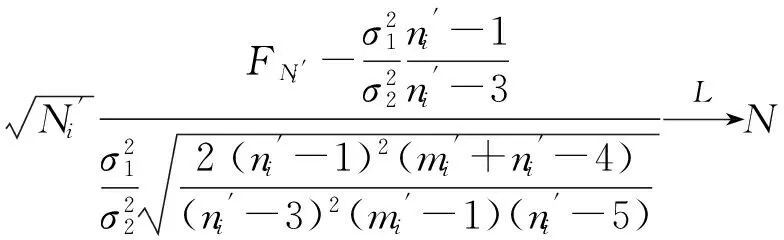
(P2) 当θi用θ0=0代替时,(P1)仍成立.
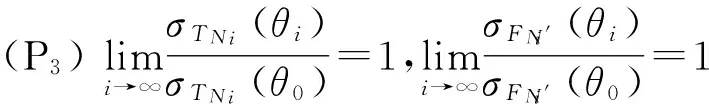

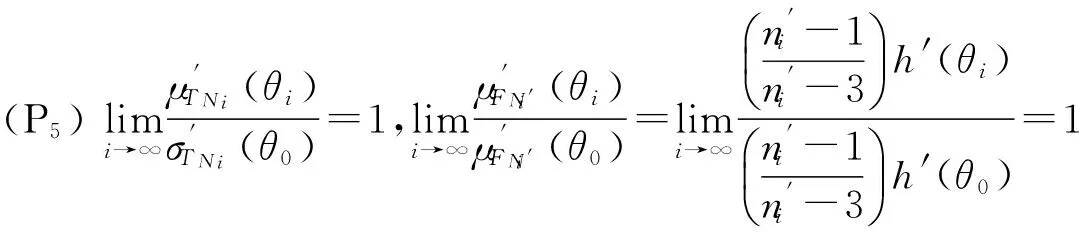
(P6)


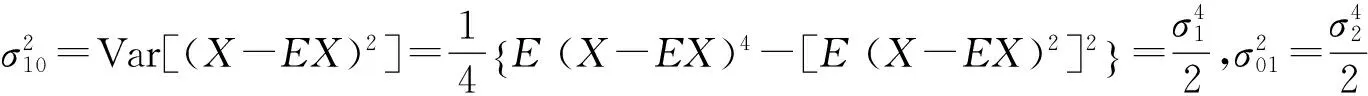
综上所述,本文给出了一种检验两个总体方差是否相等的方法,且不必要求两总体分布具有相同类型.同F检验法相比,条件明显减弱,并达到渐近相对效率为1的效果.[7]同时表明,根据U统计量的构造,说明用两个子样方差之差来检验两总体方差差异对总体是否服从正态分布具有稳健性.
[1]孙山泽.非参数统计讲义[M].北京:北京大学出版社,2000:29-41,112-115.
[2]陆媛媛,宋立新.单个总体方差差异的U统计量检验法[J].吉林大学学报(理学版),2011,49(6):1064-1067.
[3]王静龙,梁小筠.非参数统计分析[M].北京:高等教育出版社,2006:154-155.
[4]宋立新,赵志文,陈鲲.两总体分布均值相等的U统计量检验法[J].吉林大学学报(理学版),2010,48(6):957-960.
[5]陈希孺.数理统计引论[M].北京:科学出版社,2007:82-95.
[6]方开泰,许建伦.统计分布[M].北京:科学出版社,1987:186.
[7]王宏仁,宋立新,陈鲲.两个具有名义指标总体分布相等的检验[J].东北师大学报(自然科学版),2011,43(4):29-32.
(责任编辑:李亚军)
U-statistics testing method in testing the equality of two population variances of two populations
CHEN Kun1,SONG Li-xin2
(1.College of Education Science,Jilin Normal University,Siping 136000,China;2.Boda College,Jilin Normal University,Siping 136000,China)
Based on the U-statistics,a new method for testing the equality of variances of two populations is constructed. Compared to the F-testing method,it is not only applicable to more general situations,but also its asymptotic relative efficiency is equal to 1.
U-statistics;variance testing;asymptotic normality;asymptotic relative efficiency
1000-1832(2016)03-0035-06
2015-01-24
国家自然科学基金资助项目(10971084);吉林省教育厅科研项目(吉教科合字2012第369号).
陈鲲(1978—),女,博士,讲师,主要从事数理统计研究;通信作者:宋立新(1954—),男,教授,主要从事数理统计研究.
O 212.7[学科代码]110·67
A
[DOI]10.16163/j.cnki.22-1123/n.2016.03.008
