水准点稳定性F检验法与t检验法异同的研究
2010-05-17朱郭勤
张 勇 朱郭勤
(西南交通大学测量工程系, 四川成都 611756)
稳定的基准网是变形监测的关键所在,但实际上,除了设置在基岩上的标志以外,在冲积层及一些土质差的地区所设置的水准点,即使被埋设的很深,也不能认为它们一定是稳定的。国内外还有很多的膨胀土地区,在这些地区设置的水准点,也难以保持稳定不动;还有变形区域很大或变形影响范围难以确定的情况。
在这些情况下,不能无根据地以某一点作为起算点,而应根据重复观测的成果分析水准点的稳定性,从中找出较为稳定的水准点作为计算位移值的依据。通常情况下不同检验法得出的结论不一定是完全相同的,例如F检验法和t检验法得出的结果就可能不同。
1 数学模型
1.1 秩亏自由网平差模型
在控制网按间接平差中,通常有足够的起算数据,待定参数是点的坐标,他们是非随机参数,平差的数据模型是
L=BX+Δ
(1)
模型(1)的系数B阵为满秩时,则为经典的间接平差,如果出现系数阵B秩亏,那么就是相应的秩亏自由网平差。
秩亏自由网平差的函数模型为
L=BX+ΔR(B)=r (2) B的列亏数d=t-r,随即模型为 (3) 模型(2)的误差方程为 (4) (5) (5)式中N=BTPB,N+为N的伪逆,P为观测值权阵。 (1)两周期观测同一性的检验(第一步) 由每一期秩亏自由网平差的改正数可以计算该期的单位权方差 (6) 假设两周期单位权方差无显著差异(即等精度观测),将数值较大者作为分子,计算统计量 ?≤F(α,f1,f2) (7) 式中α为显著水平(一般取0.05),f1,f2为第一和第二自由度,F分位值可以查表或通过函数计算得到。如果上式成立,则接受原假设,认为两周期观测无显著差异;否则认为两周期观测不是等精度观测(可能其中一期测量误差过大),因而不能直接比较其坐标差异。 (2)计算两周期观测的综合单位权方差(第2步) (8) (3)计算间隙d的单位权方差(第3步) 每期观测分别作秩亏自由网平差求得各水准点的高程,则间隙 (9) 间隙d的协因数阵为Qd=Q1+Q2,由间隙d可按下式计算单位权方差 (10) 式中h为Qd的秩。 (4)作统计量进行整体检验(第4步) (11) 如果上式成立,则认为网中水准点都是稳定的;反之,认为网中存在动点。 (5)采用“尝试法”找出网中的动点(第5步) 将网中水准点划分为两组,即稳定点组F和动点组M,对间隙d及其权阵Pd作相应的分块,即 (12) 为把分成稳定点影响和动点影响两个统计独立的部分,采用如下变换 (13) t检验法是用来作单点位移显著性检验的一种常用的方法,它的前提是两期的观测精度相同,为此,需对两期观测数据做F检验。 第1,2步同F检验法。 第3步: 构造t检验量 ?≤tα/2 (14) 自由度f=f1+f2,i为水准点编号 若不等式成立,则认为点位稳定,否则认为点位变化显著。 由上面所述,F检验法是一种整体检验的方法,如果经检验其结果为点位变化显著,实际上指的是平均点位,并不见得全部网点的点位变化都是显著的。此时,欲用F检验法检验每个网点的稳定性,则要逐个剔除动点并做重复计算,而t检验法是一种单点检验的方法。 通常情况下,间隙差越大的点其为动点的可能性越大,比较不同检验法的优劣程度是很困难的,也不能进行直接比较,但是我们可以定义一个相对统计量来进行比较,计算检验法的相对统计量,其大者为最好[6]。现在根据相关模型计算,得到t检验法的相对统计量大于F检验法,说明t检验法剔除异常值的能力大于F检验法,故t检验法的检查的更加严密,其剔除点数一般要大于等于F检验法。下面以一个实例来说明。 有一水准点组,如图1,对其进行两期观测,观测数据见表1。发现其中有不稳定的水准点,现分别用F检验法和t检验法对其进行检验。 表1 观测数据 图1 水准点网 根据观测数据,进行分期秩亏自由网平差,其结果如下: 第1期 V1=(1.63 -2.30 2.50 -1.83)Tmm -0.13 -0.17)Tmm Qxx1= 第2期 V2=(-0.10 0.00 0.10 -0.20 -0.10 0.00 )Tmm Qxx2= H2=(7.472 1 7.498 0 7.542 7 7.807 4)Tm 根据(7)式 两周期观测无显著差异,故进行下一步分析。 根据(9)(10)式得到 d=(0.42 0.24 0.15 -0.8)Tm 根据(8)式得到综合单位权方差 根据(11)式得到 F(0.05,4,6)=4.53 得出存在动点。 表2 假设动点号与相关值 再根据(11)进行假设检验 F(α,h,f1+f2)=F(0.05,4,6)=4.53 认为通过检验。 故进行F检验法,检验出4号点为动点。 根据(14)求出每个点的t检验量(如表3)。 表3 各点t检验量 算例中,分别运用F检验法与t检验法对一组水准点进行检验,F检验法得出4号点为动点,将其剔除后便通过检验。t检验法得出1,4号为动点。这里两种方法得出不同的结论,这是说明了不同的检验法对同一个实例可能得出不相同的结论,同样也说明了t检验法剔除点数一般要大于等于F检验法的问题,笔者也从大量实验数据中看出此现象。 t检验法虽然算法简单而且更能够检测异常值,但是其有时过分的严格检验把一些沉降量稍大的也认为是动点,其检测思想单一,这点没有F检验法检验充分。故从得到结论的可靠性方面讲,F检验法是最合理的,从检测速度及尽可能多的剔除异常值方面讲,t检验法较F检验法合理。 [1]张正禄,等.工程测量学[M].武汉:武汉大学出版社,2005 [2]武汉大学测绘学院测量平差学科组. 误差理论与测量数据处理[M].武汉:武汉大学出版社,2007 [3]邱卫宁,陶本藻,姚宜斌,等.测量数据处理理论与方法[M].武汉:武汉大学出版社,2008 [4]王光伟,马 莉.拟稳平差及假设检验在高层建筑物沉降观测中的应用[J].化工施工技术,1996(6) [5]汤均博,周 立.基于matlab的拟稳平差法在沉降观测基准点检验中的应用[J].淮海工学院学报,2003(9) [6]王文周.未知σ,t检验法剔除异常值最好[J].四川工业学院学报,2000(3)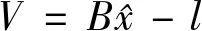
1.2 F检验法的一般步骤
1.3 t检验法的一般步骤
2 算例
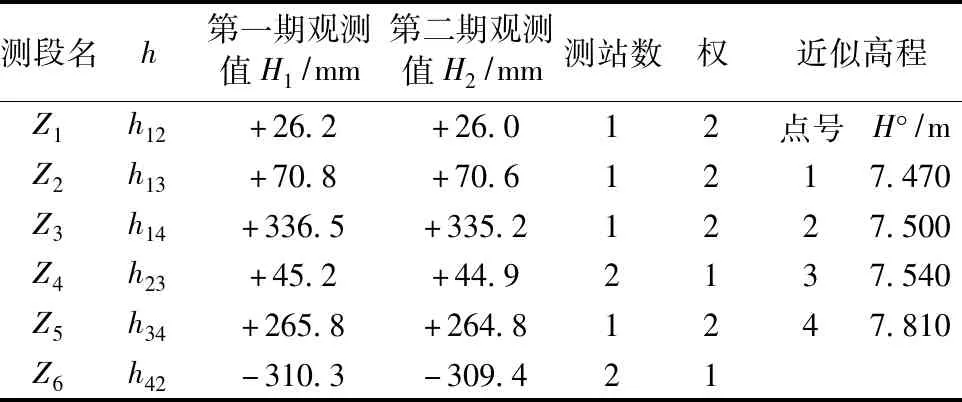
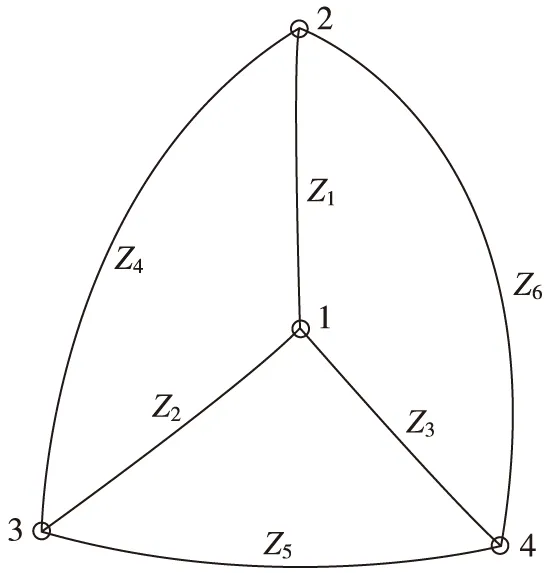


2.1 F检验法

2.2 t检验法

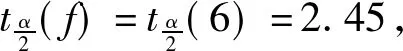
3 结论
