软硬时间窗共存装卸一体化车辆路径问题的混合离散粒子群优化算法

周　蓉,　沈维蕾

(合肥工业大学 机械与汽车工程学院,安徽 合肥　230009)



软硬时间窗共存装卸一体化车辆路径问题的混合离散粒子群优化算法

周蓉,沈维蕾

(合肥工业大学 机械与汽车工程学院,安徽 合肥230009)

文章针对软硬时间窗共存装卸一体化车辆路径问题(vehicle routing problem with simultaneous delivery and pickup under coexistence of soft and hard time windows,VRPSDPCSHTW)建立了包含车辆固定出行成本、运输成本和惩罚成本的数学模型,提出了一种混合离散粒子群优化算法。针对基本离散粒子群算法容易早熟收敛而陷入局部最优等问题,内嵌一种变邻域下降局域搜索方法,并在一定概率下执行以加强种群搜索能力，最后通过3个算例的仿真分析进行了算法验证。

车辆路径问题;装卸一体化;软硬时间窗共存;粒子群算法;变邻域下降搜索

带时间窗装卸一体化车辆路径问题(vehicle routing problem with simultaneous delivery and pickup and time windows,VRPSDPTW)是车辆路径问题的一类重要扩展。该问题涉及的客户同时具有送货和取货2种需求,并且要求服务车辆在规定的时间窗内将需求的货物送到,将待取的货物取走。如果车辆在客户要求的时间窗外到达,则存在2种情况:① 提前到达必须等待,迟到则拒绝服务,这种情况称为硬时间窗问题;② 提前到达必须等待,迟到接受服务,但无论早到或迟到都将按照违反时间的长短进行惩罚,这种情况称为软时间窗问题。现实中，不同客户对车辆服务的时间约束条件不同而使得软硬时间窗共同存在的情形经常出现,如客户的常规储备货物订货与紧急订单需求供货,前者通常是软时间窗约束,后者则是硬时间窗约束。这类问题即为软硬时间窗共存装卸一体化车辆路径问题(vehicle routing problem with simultaneous delivery and pickup under coexistence of soft and hard time windows,VRPSDPCSHTW)。

国内外有关VRPSDPTW的研究较多,而对VRPSDPCSHTW的研究较少。VRPSDPTW的求解算法大多集中在启发式和元启发式算法的研究[1]。文献[2-9]对软、硬时间窗问题分别进行了深入地研究。文献[4]对带软时间窗的装卸一体化车辆路径问题进行了求解,结果证明改进模拟退火算法比文献[2]的模拟退火算法效果更好;文献[6]对带硬时间窗的装卸一体化车辆路径问题进行了研究,并证明了混合遗传启发式算法比文献[2]的2种算法具有更好的求解性能。此外,针对软硬时间窗共存的车辆路径问题的研究并不多。文献[10]建立了软硬时间窗共存的纯配送车辆路径问题的数学模型,并证明了其提出的改进遗传算法性能的优越性;文献[11]研究了部分客户具有软时间窗或硬时间窗约束的小规模货物配送路线问题,并结合Dijkstra算法和最小权匹配算法进行求解。

粒子群优化(particle swarm optimization,PSO)算法是一种基于群体智能的自适应优化算法,在许多车辆路径问题的求解应用中已被证明具有良好的优化性能[12-15]。本文提出一种混合离散粒子群算法,将基本PSO与变邻域降序局域搜索相结合,实现在PSO完成全局空间搜索的同时进行随机化深度搜索以提高解的质量。

1　问题描述及模型

VRPSDPCSHTW描述如下:多台服务车辆装载客户需要的货物从物流中心出发,在客户规定的时间内送至各客户处,并将客户供应的货物在规定时间内从各客户处取走送至物流中心;每个客户位置一定,货物需求量和供应量一定;每辆车的载重量一定,1次配送最大行驶距离一定;部分客户的服务时间窗约束为软时间窗,其余客户为硬时间窗;要求合理安排车辆配送路线,使目标函数得到优化,并满足以下约束条件:① 容量限制,即配送过程中配送车辆载货量不超过其最大载重量;② 行驶距离限制,即每条配送路径长度不超过车辆一次配送最大行驶距离;③ 每个客户需求的货物必须送到,供应的货物必须取走。本文以总配送成本最小为目标,研究单一物流中心问题。

根据上述描述,假设物流中心共有N个客户点,i、j为各客户的编号,0为物流中心编号;各客户点配送需求量为di,货物供应量为pi,单车最大装载量为Q;各客户点间距离为cij,各点服务时间为si,物流中心到客户点i的距离为c0i;单车单位行驶距离成本为g,单车单次出行成本为f,单车最大行驶距离为L;所用车辆数为K,车辆k到达客户点i的时间为Tik,在节点i的等待时间为tik,车辆k在i、j间的行驶时间为tijk,车辆k离开客户点i时车上载重量为Uik;客户点i的时间窗为[TEi,TLi]。若客户i为软时间窗约束,车辆k提前到达的惩罚因子为w1i,迟到惩罚因子为w2i。若客户i为硬时间窗约束,车辆k迟到的惩罚因子为M(M为一个很大的正数)。

本文以总配送成本最小为目标，建立VRPSDPCSHTW混合整数规划模型如下：

(1)

满足如下约束条件:

(2)

(3)

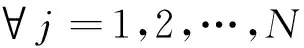
(4)

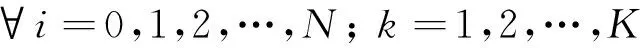
(5)

(6)

(7)

(8)

(9)

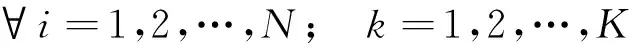
(10)

(11)

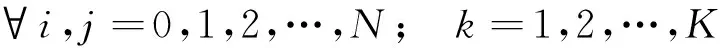
(12)

(1)式为考虑了车辆固定成本、运输成本及包含了软硬时间窗惩罚项的总配送成本最小目标,其中ei、ei′分别为节点i的软、硬时间窗性质,当ei=1且ei′=0时节点i为软时间窗约束,当ei′=1且ei=0时节点i为硬时间窗约束;(2)式表示每个客户都必须被服务1次,且每个客户仅由1辆车来服务;(3)式表示所有路径数不超过车辆总数K;(4)式为流量守恒式;(5)式表示车辆在行驶过程中,在任一客户点的载重量都不能超过车容量Q;(6)式和(7)式用来限制每辆车的总配送装载量与总供应装载量都不得超过车容量Q;(8)式保证每辆车的配送距离不得超过车辆最大行驶距离;(9)式表示车辆k到达节点i的时间;(10)式表示车辆k提前到达节点i的等待时间;(11)式表示硬时间窗约束;(12)式表示决策变量为0或1的整数限制式。

2　算法设计

2.1离散粒子群算法基本原理

PSO算法是一种受到鸟群觅食行为启发的进化算法,通过个体间信息互动使群体达到最优。基本PSO算法适用于连续问题优化求解,而实际工程组合优化问题一般为离散域问题,因而出现了重新定义PSO算法操作算子的DPSO离散策略[16]。DPSO用基于问题的一个排列作为粒子的一个位置,用问题的所有排列构成问题的搜索空间,并借鉴进化算法的操作方式,通过遗传变异和交叉操作实现3部分信息的综合影响,具体位置更新公式[14]为:

(13)

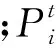
2.2混合离散粒子群算法

本文提出一种混合离散粒子群算法(HDPSO),该算法将PSO算法与局域搜索相结合求解VRPSDPCSHTW。混合算法的本质在于局域搜索作为个体粒子的一种概率变异操作,即在PSO算法中以一定概率执行局域搜索,算法步骤如下。

(1) 初始化种群参数Ps、变异概率w、交叉概率c1和c2、局域搜索概率pLS、最大迭代次数IteMax、全局极值连续未更新最大次数gSucNum。

(3) 判断是否满足终止条件。若gNotImpv> gSucNum且t> Itemax，则满足终止条件,转步骤(5);否则不满足终止条件,转步骤(4)。

(5) 输出全局极值粒子gX、全局极值gCOST以及最优配送方案。

2.2.1解的表示、解码与评价

(1) 解的表示。本文采用文献[17]提出的基于客户直排大路径解表示方法。对于具有N个客户的VRPSDPCSHTW,直接产生N个1 ～N之间互不重复自然数的排列而形成一条大路径,表示客户顺序,然后在大路径最前面加上0(表示物流中心)形成带物流中心的大路径。

(2) 解码。深度优先搜索方法是一种大路径分割方法[18],本文根据研究问题的约束条件,包括车辆的最大载重量约束、车辆一次服务的最大行驶距离约束以及客户要求服务的时间窗约束,对深度优先搜索大路分割方法稍作修改,使其适用于VRPSDPCSHTW。

(3) 解的评价。本文以目标函数值Z作为解的评价值。

2.2.2种群初始化

本文采用改进节约法和随机产生2种方法构造初始种群。改进节约法是在C-W节约法基础上,综合考虑车辆总行驶距离、时间窗、同时取送货以及车辆容量限制等约束因素,重新定义节约值[19]。采用该改进节约法时,通过设定不同的参数取值产生一定数量的初始大路径解,剩余的初始种群采用随机方法生成。

2.2.3位置更新准则

采用(13)式实现粒子的位置更新,具体更新规则为:当变异概率小于或等于w时执行自身变异操作,否则不执行;当个人交叉概率小于或等于c1时与个人极值执行F2交叉操作,否则不执行;当全局交叉概率小于或等于c2时与全局极值执行F3交叉操作,否则不执行。

变异操作采用两点插入式变异,即任意选择变异粒子中的2个位置,变异时首先将变异粒子中2个位置之间的所有元素按原顺序放置到最前面,然后依次按原顺序插入第1个位置前的所有元素、所选择2个位置上的元素、第2个位置后的所有元素,便得到变异后粒子。

本文采用PTL两点交叉操作[14],可以使相同序列交叉后得到不同的新序列。

2.2.4局域搜索

本文以两点换位[2]、2-OPT 2种邻域机制为基础,设计了一种简单的变邻域下降局域搜索方法,其搜索流程为:首先对局域搜索粒子采用两点换位机制,如果交换后的新粒子目标函数值比交换前降低,则以新粒子位置代替交换前的粒子位置,否则执行2-OPT邻域机制。

3　实验计算和结果分析

3.1算例选取及实验参数设置

选取文献[4]的单纯软时间窗算例作为算例1,文献[2]与文献[6]的单纯硬时间窗算例作为算例2,根据文献[4]的算例修改后的软硬时间窗共存算例作为算例3。其中,算例1要求以配送总里程最短为目标安排车辆配送路线;算例2要求以配送总距离最短为目标安排车辆配送路线;算例3是在算例1的基础上,随机选取客户点3、8、14将其设为硬时间窗约束,其余客户点仍为软时间窗约束,时间窗数据不改变,以配送总里程最短为优化目标。

经测试设置参数为:Ps=20,pLS=0.3,w=0.2,c1=c2=0.6，最大迭代次数IteMax=1 000,全局极值连续未更新最大次数gSucNum=20。

3.2计算结果分析

3.2.1算例1分析

算例1的10次计算平均结果见表1所列,其中“偏差百分比”的计算公式为:

偏差百分比=

表1　算例1分析结果

由表1可知,与文献[4]提出的SA相比,本文算法求得的近似最优解更好、平均值更优,但本文算法比SA的平均等待及迟到时间要长一些。该问题的改善可以通过改变相应权重来减少相应时间,如增大等待/迟到惩罚因子来减少等待/迟到时间。

3.2.2算例2分析

算例2的平均计算结果见表2所列。由表2可以看出,本文算法得到的最优配送距离最短、使用车辆数最少。因此在求解单纯硬时间窗车辆路径问题时,本文算法的性能优于文献[6]提出的HGHA、文献[2]提出的Tabu和SA等算法。本文算法得到的近似最优解共有5条配送路径:0-6-26-40-20-21-1-27-7-0;0-33-2-3-11-31-28-0;0-9-29-38-18-30-10-23-36-16-22-0;0-13-25-24-37-17-39-19-4-5-35-15-0;0-14-34-8-32-12-0。累积等待时间为29.38 h,累积迟到时间为0。

表2　算例2分析结果

3.2.3算例3分析

本文算法和文献[10]算法对算例3平均计算结果的对比分析见表3所列,其中偏差百分比计算方式同表1,成本标准差、里程标准差分别为10次计算结果的总配送成本标准偏差、总配送里程标准偏差。由表3可知,无论是以总配送里程最短还是以总配送成本最小为目标,本文算法在寻优质量、计算速度以及计算稳定性方面都比文献[10]的GA算法更好。采用本文算法得到该问题的最优配送里程为109.3 km,总配送成本为192.2元,对应最优配送路线为:0-14-8-0;0-6-20-1-7-12-0;0-9-18-11-10-3-2-0;0-13-19-17-16-4-5-15-0。累积等待时间为1.27 h,累积迟到时间为0。

表3　算例3平均计算结果的对比分析

4　结　　论

本文构建了软硬时间窗共存的装卸一体化车辆路径问题模型,提出了求解该模型的混合离散粒子群算法,将变邻域下降局域搜索方法与基本离散粒子群算法相结合,有效避免了粒子群算法早熟收敛、陷入局部最优。通过单纯的软、硬时间窗问题及软硬时间窗共存问题3个算例的仿真测算,验证了本文设计算法的求解性能。本文算法对于具有不同时间约束服务的物流配送和取货优化问题具有一定的指导意义。

[1]郎茂祥.物流配送车辆调度问题的模型和算法研究[D].北京:北方交通大学,2002.

[2]PARRAGH S N,DOERNER K F,HARTL R F.A survey on pickup and delivery problems:part Ⅰ:transportation between customers and depot [J].Journal Für Betriebswirtschaft,2008,58(1):21-51.

[3]祁文祥,陆志强,孙小明.带软时间窗的集货与送货多车辆路径问题节约算法[J].交通运输工程学报,2010,10(2):99-103,109.

[4]邓爱民,毛超,周彦霆.带软时间窗的集配货一体化VRP改进模拟退火算法优化研究[J].系统工程理论与实践,2009,29(5):186-192.

[5]张丽艳,庞小红,夏蔚军,等.带时间窗车辆路径问题的混合粒子群算法[J].上海交通大学学报,2006,40(11):1890-1894,1900.

[6]胡大伟,陈诚,王来军.带硬时间窗车辆路线问题的混合遗传启发式算法[J].交通运输工程学报,2007,7(5):112-117.

[7]赵达,李军,马丹祥,等.求解硬时间窗约束下随机需求库存-路径问题的优化算法[J].运筹与管理,2014,23(1):26-32,38.

[8]龙汀,潘若愚.蚁群算法求解带时间窗的配送路径问题[J].合肥工业大学学报(自然科学版),2008,31(7):1042-1046.

[9]LAI M Y,CAO E B.An improved differential evolution algorithm for vehicle routing problem with simultaneous pickups and deliveries and time windows[J].Engineering Applications of Artificial Intelligence,2010,23(2):188-195.

[10]史昊,何俊生,马畅.求解软硬时间窗共存配送路径问题的改进遗传算法[J].山东交通学院学报,2013,21(2):14-18.

[11]杨容浩,范俊波,杨佳,等.一种带有时间窗的货物配送路线设计算法[J].交通运输工程与信息学报,2005,3(1):30-35.

[12]张其亮,陈永生.基于混合粒子群-NEH算法求解无等待柔性流水车间调度问题[J].系统工程理论与实践,2014,34(3):802-809.

[13]邱晗光,张旭梅.基于改进粒子群算法的开放式定位-运输路线问题研究[J].中国机械工程,2006,17(22):2359-2361.

[14]PAN Q K,TASGETIREN M F,LIANG Y C.A discrete particle swarm optimization algorithm for the no-wait flowshop scheduling problem[J].Computers and Operations Research,2008,35(9):2807-2839.

[15]AI T J,KACHITVICHYANUKUL V.A particle swarm optimization for the vehicle routing problem with simultaneous pickup and delivery[J].Computers and Operations Research,2009,36(5):1693-1702.

[16]郭文忠,陈国龙,陈振.离散粒子群优化算法研究综述[J].福州大学学报(自然科学版),2011,39(5):631-638.

[17]PRINS C.A simple and effective evolutionary algorithm for the vehicle routing problem [J].Computers and Operations Research,2004,31(12):1985-2002.

[18]DUHAMEL C,LACOMME P,PRODHON C.Efficient frameworks for greedy split and new depth first search split procedures for routing problems[J].Computers and Operations Research,2011,38(4):723-739.

[19]庄英群.应用禁忌搜索法于混合送收货之车辆途程问题[D].台中:逢甲大学,2003.

(责任编辑胡亚敏)

Hybrid discrete particle swarm optimization algorithm for vehicle routing problem with simultaneous delivery and pickup under coexistence of soft and hard time windows

ZHOU Rong, SHEN Weilei

(School of Machinery and Automobile Engineering, Hefei University of Technology, Hefei 230009, China)

In this paper, a general mathematical model of the vehicle routing problem with simultaneous delivery and pickup under coexistence of soft and hard time windows(VRPSDPCSHTW), which contains fixed cost, travel cost and punished cost of vehicles, was established. And a hybrid discrete particle swarm optimization algorithm was proposed. In order to solve the problems of premature convergence and easily falling into local minimum in the basic discrete particle swarm optimization algorithm, a simple variable neighborhood descent search algorithm as a local search procedure was embedded in the basic algorithm and was carried out under a certain probability. Finally, the performance of the proposed method was examined by three numerical cases.

vehicle routing problem; simultaneous delivery and pickup; coexistence of soft and hard time windows; particle swarm optimization; variable neighborhood descent search

2015-03-31；

2015-05-04

国家自然科学基金资助项目(71071046)

周蓉(1977-),女,四川德阳人,博士,合肥工业大学讲师.

10.3969/j.issn.1003-5060.2016.08.004

TP18

A

1003-5060(2016)08-1022-05