基于三次有理PH曲线的G2Hermite插值

马淑娟,　唐　烁

(合肥工业大学 数学学院,安徽 合肥　230009)



基于三次有理PH曲线的G2Hermite插值

马淑娟,唐烁

(合肥工业大学 数学学院,安徽 合肥230009)

文章在满足G1Hermite插值条件的三次有理PH曲线的基础上,通过简单的方法构造了一个满足G2Hermite插值条件的三次有理Bézier曲线。该方法只需根据始末端点的曲率来确定曲线的权重进而得到插值曲线,具有很好的几何意义,数值实例表明了该算法的有效性。

有理PH曲线;Bézier曲线;G1Hermite插值;G2Hermite插值

已知端点数据的Hermite插值是计算机辅助几何设计(computeraidedgemetricdesign,CAGD)中一种常用的构造曲线的方法。又因为有理Bézier曲线是系统中常用的一种模型,所以近年来，关于有理Bézier曲线的Hermite插值问题得到了研究[1-3]。

关于G2Hermite插值,文献[4]提出了二阶几何平面三次Bézier曲线插值,通过求解二元二次方程组得到满足插值条件的曲线表达式;文献[5]拓展该方法提出了三次有理Bézier曲线,但该方法并未降低解的存在条件;文献[6]通过增加自由度使曲线满足G2插值条件;文献[2]在三次有理Bézier曲线满足G1Hermite插值条件的基础上，增加2个自由度使其满足G2Hermite插值条件,但是其端点处切向量与X轴夹角和不能超过2π/3,且解的存在性条件比较高;文献[7]在G1Hermite插值基础上,拓展成4个自由度,解的存在性条件依然比较高;文献[8]提供了一种用2条二次有理曲线升阶的方法来构造满足G2Hermite插值条件的三次有理Bézier曲线,这种方法具有很好的几何性质,但是因为引入交点b,限制了该曲线只能是C型,即曲线的控制多边形只能是凸四边形, 所以该方法不适用于构造S型曲线。

文献[9]提出了有理PH曲线,并给出了该类曲线的统一表达式。有拐点的PH曲线次数至少为5。本文在文献[3]的基础上,利用PH曲线的复数表示给出满足G1Hermite插值条件的三次有理PH曲线,并根据曲线始末端点的已知曲率来调节曲线权重，从而得到满足G2Hermite条件的插值曲线,得到的插值曲线与三次有理PH曲线有相同的控制顶点，进而有相同的控制多边形。该方法有很好的几何性质，可广泛应用于计算机数值控制与加工、离散插值计算、运动路径控制等技术中。

1　预备知识

1.1三次有理PH曲线的G1Hermite插值

定义1平面上的有理参数曲线c(t)=(x(t),y(t))称为有理PH曲线,是指存在有理函数R(t),使得[3]：

类似于多项式PH曲线,有理PH曲线也具有一些很好的性质,例如:有理PH曲线的等距曲线是有理曲线;有理PH曲线在正交和平移变换、等比例缩放以及分式线性参数变化下仍为有理PH曲线[10]。

定理1设

记(b0,T0;b3,T1)为G1Hermite插值条件，其中，b0、b3为始末端点坐标,T0、T1为相应的单位切向量,因为有理PH曲线在正交变换、平移变换及等比例缩放下仍为有理PH曲线，且分式线性参数变换不改变有理PH曲线的性质，所以可以假定w0=w3=1,此时,三次有理PH曲线可以写成如下形式：

其中,t∈(0,1)，由定理1存在复系数多项式z(t)=z0(1-t)2+2z1(1-t)t+z2t2，满足:

(1)

其中,z0=r0eiα；z1=r1eiθ；z2=r2eiβ，rj>0；α，β∈(-π/2,π/2);θ∈(-π,π)。

则由G1Hermite插值条件知2α、2β分别是已知两端点切方向的辐角,即arg(T0)=2α,arg(T1)=2β。

1.2三次有理Bézier曲线表达式

根据文献[12]，三次有理Bézier曲线可写成如下形式：

若三次有理Bézier曲线控制多边形如图1a所示,则曲线为C型；若控制多边形如图1b所示,则曲线为S型。其中bi(i=0,1,2,3)为曲线控制顶点,曲率公式为:

(2)

始末端点的曲率只需分别令t=0,t=1,带入(2)式可得:

(3)

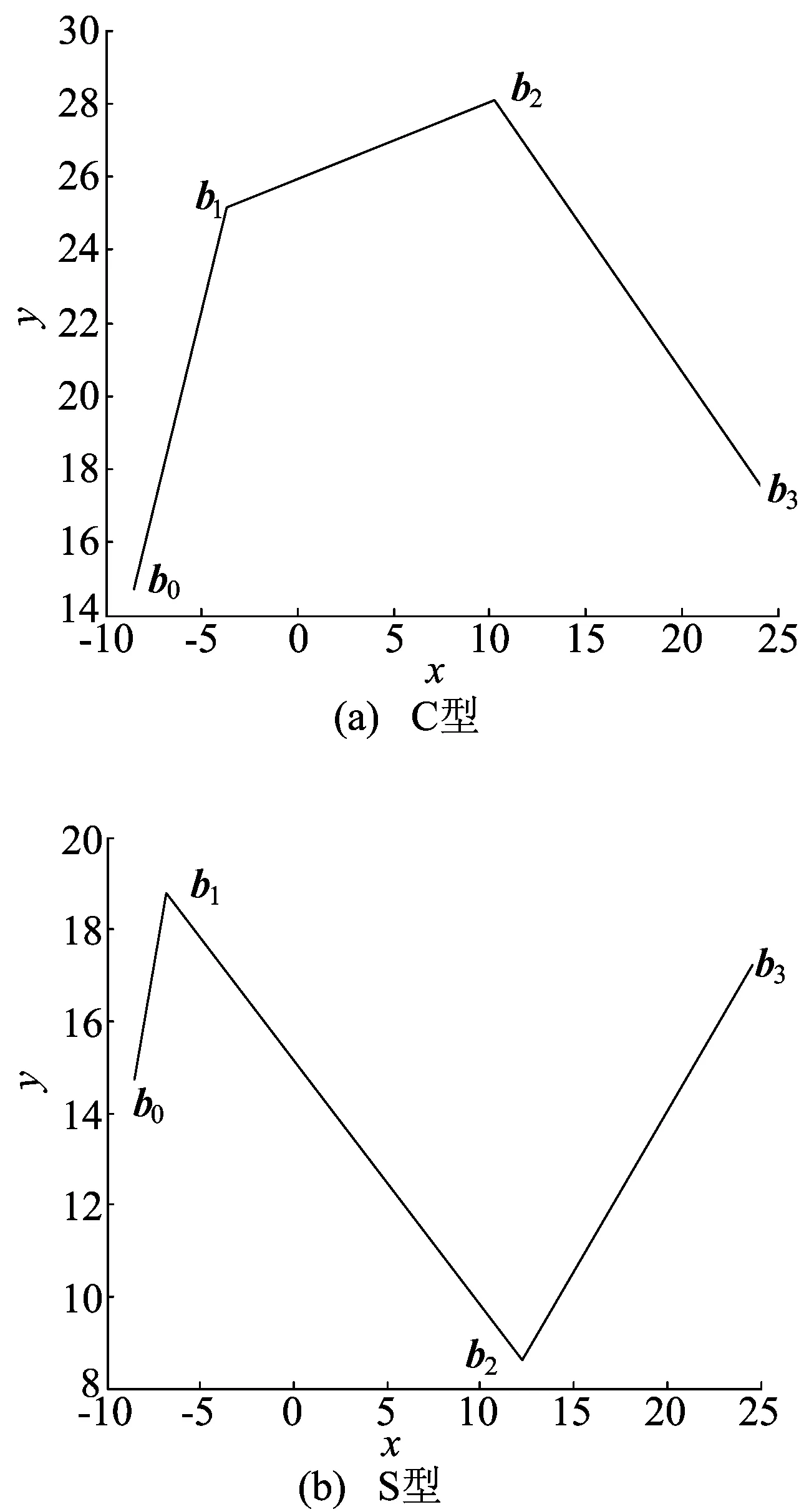
图1　曲线控制多边形

2　三次有理Bézier曲线G2Hermite插值

构造G2Hermite插值曲线,实际上是寻找一个参数曲线,该曲线在满足G1Hermite插值条件下,曲线始末2个端点还要满足相应的曲率。

假设三次有理Bézier曲线g(t)的G2Hermite插值条件为(b0,T0,k0;b3,T1,k1),其中k0、k1为始末端点的曲率。由上述提到的三次有理Bézier曲线的表达式可知,只需确定曲线控制顶点及权重便可确定曲线,因此令满足G2Hermite插值的三次有理Bézier曲线g(t)与满足G1Hermite插值的三次有理PH曲线有相同的控制顶点,进而会有相同的控制多边形。然后通过类似的方法[3],计算出权重w1、w2的值,使得三次有理Bézier曲线g(t)满足G2Hermite插值。

下面首先给出一种构造满足G1Hermite插值的三次有理PH曲线的方法。通过比较(1)式的系数,并由解的对称性可得:

(4)

综合以上3个方面可以得到如下的分类:

(1) 当z0z2=1时,有r0r2=1且α+β=0,此时,r0=r2=1,r1=|cosα|,θ=0,可以验证插值曲线表示一段圆弧。

(3) 当z0z2≠1时,若r0r2≠0且α+β≠0,有如下情况:

当tanαtanβ≤0,且α+β<0,有

当tanαtanβ≤0,且α+β>0,有

C型三次有理PH曲线得以确定。

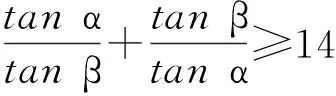
S型三次有理PH曲线得以确定。

其中,A=cos(α-β)+cos(α+β);

C=cos(α-β)-cos(α+β)。

根据不同的已知条件,满足相应的关系可以得到θ的值,由α、β、θ的值可以算得r0、r1、r2的值,即

其中

由z0=r0eiα,z1=r1eiθ,z2=r2eiβ可以获得曲线的控制顶点,因此满足G1Hermite插值条件的曲线控制多边形及表达式也随之确定了。

以下讨论在已知始末端点曲率的基础上确定满足G2Hermite插值条件的曲线权重。为了方便选择与G1Hermite相同的坐标系,(3)式可以写成如下形式:

(5)

其中

根据插值条件可知k(0)、k(1)为已知,C0、C1可由上述满足G1Hermite插值的三次有理PH曲线得到,而w1′、w2′的计算公式为：

(5)

但是w1、w2的符号与曲线的类型有关系,若曲线为C型,则w1、w2同号;若曲线为S型,则w1、w2异号。因此有定理2。

定理2给定G2Hermite条件(b1,T0,k0;b3,T1,k1),β∈(-π/2,π/2),α∈(0,π/2,),若α、β满足:

或满足:

则存在唯一的三次有理Bézier曲线:

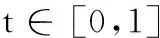
满足G2Hermite条件,其控制多边形与三次有理PH曲线相同。

下面给出三次有理Bézier曲线的G2Hermite插值算法。

输入:G2Hermite插值条件(b1,T0,k0;b3,T1,k1)。

输出:满足插值条件的三次有理Bézier曲线。

算法步骤如下:

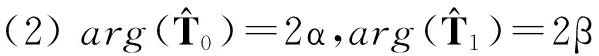
(3) 若α、β满足α+β=0转步骤(4),否则转步骤(5)。

(5) 若tanαtanβ≤0且α+β<0,则有:

否则转步骤(6)。

(6) 若tanαtanβ≤0且α+β>0,则有:

否则转步骤(7)。

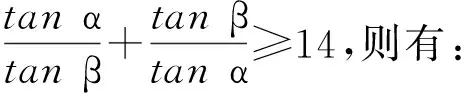
否则转步骤(14)。

(8) 将α、β、θ的值带入下式:

其中

(9) z0=r0eiα,z1=r1eiθ,z2=r2eiβ。

(12) 确定曲线权重为：

(13) 获得G2Hermite插值曲线。

(14) 原插值条件无解。

3　数值实例

例1G2Hermite插值条件为:

b0=(-15.39,42.29),b3=(28.19,10.26),

该条件中α、β大小相同,因此满足G1Hermite插值条件的三次有理PH曲线有2个解,一个解是圆弧，如图2所示,另一个退化为多项式曲线，如图3所示。

图2　PH曲线为圆弧

图3　PH曲线为多项式

图中实线表示满足G1Hermite插值条件的三次有理PH曲线,虚线表示满足G2Hermite插值条件的三次有理Bézier曲线。

利用解的控制顶点,再由已知曲率值k0=0.5,k1=0.4便可得到满足G2Hermite插值条件的三次有理Bézier曲线的权重,此时即可得到满足插值条件的曲线表达式。

例2G2Hermite插值条件为:

b0=(-5.81,15.97),b3=(22.98,19.28),

根据已知条件可知α、β满足tanαtanβ≤0,α+β<0,因此已知条件的插值曲线有解,代入数据可得到一条C型三次有理Bézier曲线如图4所示。当k0=1,k1=0.2时本文方法与文献[8]提出的方法得到的曲线做曲率对比如图5所示。通过对比可以看出,用本文方法比用文献[8]方法所得曲线的曲率变化明显平缓很多。

图4　α+β<0时，PH曲线为有理C型曲线

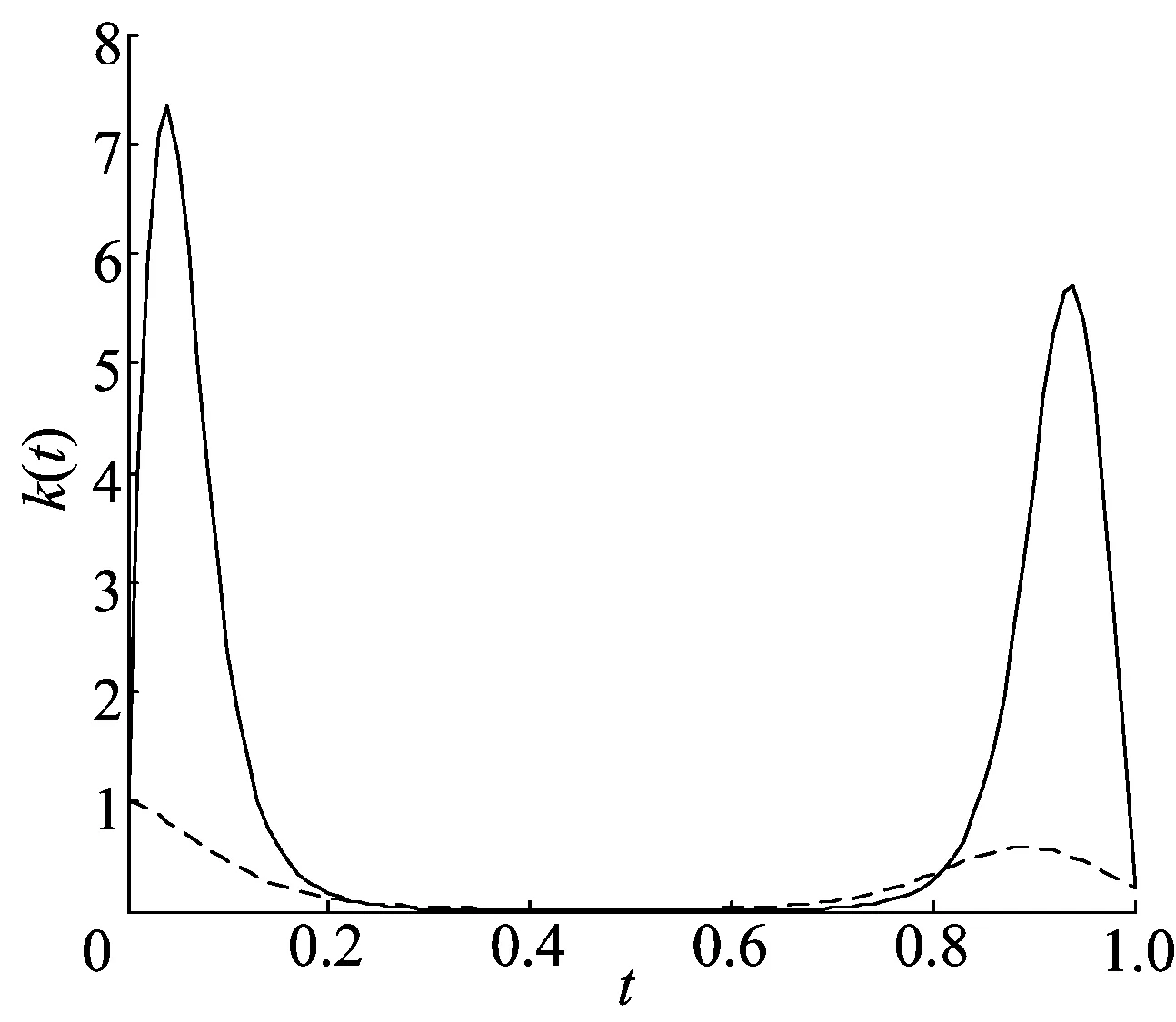
图5　k0=1,k1=0.2时曲率对比

例3G2Hermite插值条件为:

b0=(-8.5,14.72),b3=(24.57,17.21),

根据已知条件可知α、β满足tanαtanβ≤0,α+β>0，因此已知条件的插值曲线有解,代入已知数据可得到一条C型三次有理Bézier曲线如图6所示。当k0=0.3,k1=0.2时本文方法与文献[8]提出的方法得到的曲线做曲率对比如图7所示。通过对比可以看出,用本文方法比用文献[8]方法所得曲线的曲率变化明显平缓很多。

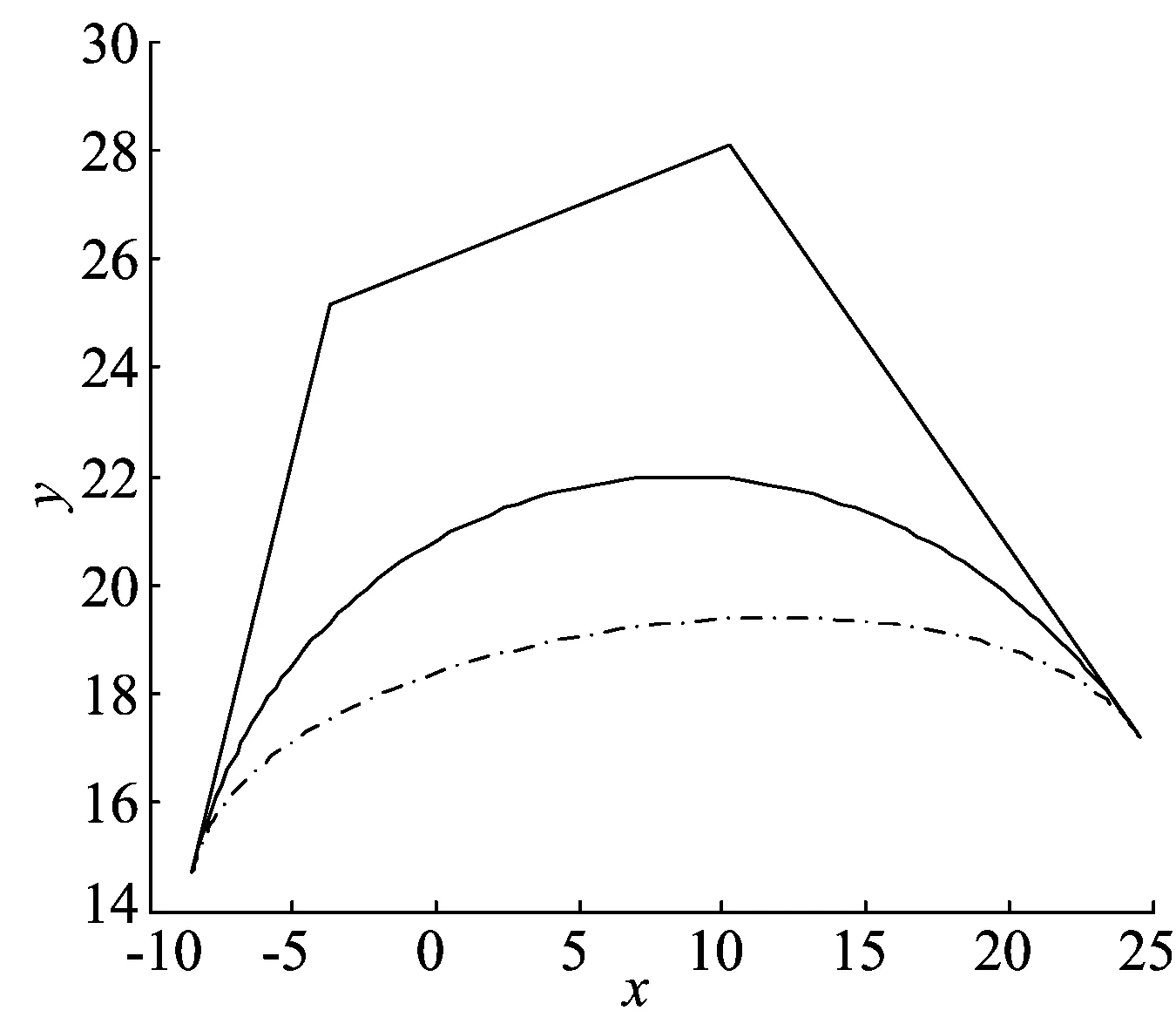
图6　α+β>0时，PH曲线为有理C型曲线

图7　k0=0.3,k1=0.2时曲率对比

例4G2Hermite插值条件为:

b0=(-17.37,36.03)，b3=(26.53,27.21),

k0=0.005,k1=0.01。

由已知条件端点曲率k0、k1的值可知,欲求的插值曲线应为一条S型曲线,又因为α、β的值满足上述所提到的S型曲线有解条件,故满足此已知条件的三次有理Bézier曲线如图8所示。

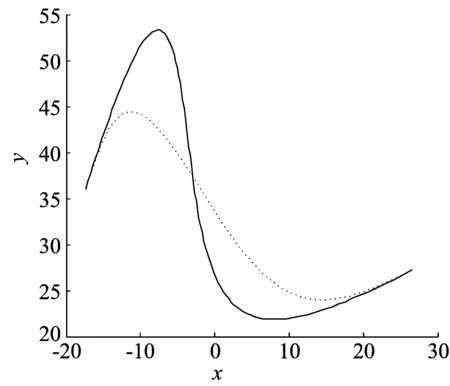
图8　PH曲线为有理S型曲线

4　结　论

在满足G1Hermite插值条件的三次PH曲线基础上，本文构造了一个满足G2Hermite插值条件三次有理Bézier曲线的简单方法。在讨论过程中可知，该方法可以将三次多项式PH曲线转化成三次有理Bézier曲线,但此时的Bézier曲线只能为C型。因为Bézier曲线的控制顶点与PH曲线控制顶点一样,所以它们的控制多边形也一样；但是曲线权重取决于始末端点处的具体曲率数值。这种方法能得到唯一且精确的解,并具有很好的几何性质。

方法的不足之处在于构造PH曲线时初始条件受限制,可能会出现无解的情况。这时可以通过文献[13]的方法插入满足条件的中间数据来构造段数最少的PH样条曲线的方法, 以达到G1插值的目的；然后再在每个节段用文献[8]方法得到满足G2插值的三次有理Bézier曲线。

[1]FARING.Curvesandsurfacesforcomputeraidedgeo-metricdesign[M].NewYork:AcademicPress,1996.

[2]FARING.GeometricHermiteinterpolationwithcircularprecision[J].Computer-AidedDesign,2008,40(4):476-479.

[3]潘俊.有理三次PH曲线的G1Hermite插值[J].复旦大学学报(自然科学版),2007,46(2):184-191.

[4]DEBOORC,HOLLINK,SABINM.HighaccuracygeometricHermiteinterpolation[J].ComputerAidedGeometricDesign,1987,4(4):269-278.

[5]DEGENWLF.Highaccuraterationalapproximationofparametriccurves[J].ComputerAidedGeometricDesign1993,10(3/4):293-313.

[6]SAKAIM.Osculatoryinterpolation[J].ComputerAidedGeometricDesign，2001,18(8):739-750.

[7]WALTONDJ,MEEKDS.G2Hermiteinterpolationwithcircularprecision[J].Computer-AidedDesign,2010,42(9):749-758.

[8]LIYajuan,DENGChongyang,MAWeiyin.C-shapedG2HermiteinterpolationbyrationalcubicBéziercurvewithconicprecision[J].ComputerAidedGeometricDesign,2014,31(5):25-8-264.

[9]POTTMANNH.Rationalcurvesandsurfacewithrationaloffsets[J].ComputerAidedGeometricDesign,1995,12(2):175-192.

[10]孙露露.关于PH曲线插值若干问题的研究[D].合肥:合肥工业大学,2010.

[11]FAROUKIRT,NEFFCA.Hermiteinterpolationbypythagoreanhodographquintics[J].MathematicsofComputation,1995,64(212):1589-1609.

[12]PIEGLL,TILLERW.TheNURBSbook[M].2nded.NewYork:Springer-Verlag,1997.

[13]马元魁,张天平,康宝生.C1插值平面三次PH样条的构造 [J].西安工业大学学报,2007,27(1):34-37,51.

(责任编辑张镅)

G2HermiteinterpolationbasedonrationalcubicPHcurve

MAShujuan,TANGShuo

(SchoolofMathematics,HefeiUniversityofTechnology,Hefei230009,China)

BasedontheG1HermiteinterpolationbyarationalcubicPythagorean-hodograph(PH)curve,asimplemethodforG2HermiteinterpolationbyarationalcubicBéziercurveispresented,whichhasawell-understoodgeometricalmeaning.Inthismethodtheweightsofthecurveareacquiredbythecurvaturesatboththestartingpointsandendpoints.Theeffectivenessofthealgorithmisverifiedbynumericalexamples.

rationalPythagorean-hodograph(PH)curve;Béziercurve;G1Hermiteinterpolation;G2Hermiteinterpolation

2015-03-27；

2015-06-06

国家自然科学基金资助项目(61272024)

马淑娟(1990-),女,安徽宿州人,合肥工业大学硕士生；

唐烁(1964-),男,安徽巢湖人,合肥工业大学教授,硕士生导师.

10.3969/j.issn.1003-5060.2016.08.027

TP391.72

A

1003-5060(2016)08-1142-06