复合型工程科技人才评价模型研究

张　利,　徐　娟,　吕格格,　黄景荣



复合型工程科技人才评价模型研究

张利1,徐娟2,吕格格1,黄景荣3

(1.合肥工业大学 机械与汽车工程学院,安徽 合肥 230009; 2.合肥工业大学 计算机与信息学院, 安徽 合肥 230009; 3.合肥工业大学 创新学院, 安徽 合肥230009)

复合型人才培养的评价体系对高校选择培养机制有着指导性作用。文章应用层次分析法在决策模糊问题上定性与定量相结合的优点,采用重要度内积概念来定义直观两元素之间的重要度比值,构建了基于管理体系、环境平台、教学模式、实践应用及培养效果等准则的重要度权重,建立了一种评价高校复合型工程科技人才培养指标体系的模型,并通过构造判断矩阵进行一致性检验以验证模型的准确性,为评价高校复合型人才培养水平提供参考。

层次分析法;判断矩阵;权重;评价指标体系;重要度内积

0　引　　言

进入21世纪以来,复合型人才的培养开始受到人们的广泛关注。科学合理的复合型人才培养评价指标体系能够为高校人才培养模式的调整提供决策参考,从而有利于提高高校培养人才质量[1]。目前有关复合型人才培养评价存在指标量化缺乏系统性、定性和定量分析不充分等缺陷,层次分析法可以很好地解决这些问题[2]。文献[3]利用指标体系和层次分析法(analyticalhierarchyprocess,AHP)解决了洱海流域水环境承载力评估问题；文献[4]研究了基于层次分析法的应用型人才培养评价问题；文献[5]在校园网络安全评估指标体系研究中利用可拓层次分析法解决了校园网安全评估指标体系的问题。

本文基于AHP构建层次函数映射关系,在提出重要度内积概念的基础上计算层次权重,进而建立复合型工程科技人才培养的评价模型,为高校复合型人才培养评价提供参考。

1　层次分析法基本原理

AHP是20 世纪 70 年代初由美国著名运筹学家萨蒂提出的。该方法显著优点是将定性问题定量化,把复杂问题分成若干有序层次,将直观认识从简单到复杂层层累加,最终模仿人脑决策问题。

AHP的基本思路是根据对客观现象的判断,就某一层次上的排列因素对高层次因素的相对重要性做出表述,即构造各层的比较判断矩阵,继而根据这一矩阵的最大特征根及特征向量来确定每一层次中各因素相对重要性的次序权重。最后,通过对各层的分析得到整个问题的总排序权重,从而为决策者提供数量化的决策依据[6]。

AHP分析步骤如下:

(1) 构建层次模型。首先确定模型层数设为n,然后整理评价指标确定层次位置与关系,根据AHP的特点可知,下层(X)与上层(Y)之间满足的函数映射关系为:

(1)

即Y对应的X可以有n个X值,但下层的X有且只有一个上层的元素,当n=1时,无需再进一步分层,Y作为最底层。

(2) 构造判断矩阵。所需判断矩阵的个数n与模型层数n和层元素个数m有关。判断矩阵元素取值为重要度内积。定义内积(Xi,Xj)=(Xi+Xj)/Xi-1为Xi相较于Xj在A层次中的重要度,则(Xi,Xi)=(Xi+Xi)/Xi-1=1。所计算值对应的是判断矩阵中的数值,若判断矩阵中(X2,X1)=a,则(X1,X2)=1/a。显然内积值大于0。另外根据重要度内积定义可知,若Xi比Xj重要值为 t,则Xj比Xi重要值为1/t。内积大小见表1所列,内积取值则根据表1所列进行判断。

表1　内积大小

验证判断矩阵合理性并计算权重步骤如下:

(1) 将判断矩阵行元素(即每行全部内积值)相乘,具体公式为:

(2)

(2) 计算权重，其公式为:

(3)

由此得出对应的权重向量为：

(3) 层次单排序与一致性检验。验证判断矩阵在逻辑上是合理的,若不符合一致性要求则要调整判断矩阵。所须检验的值是一致性指标大小，一致性指标CI的计算公式[7]为:

(4)

一致性指标比率CR计算公式为:

CR=CI/RI

(5)

其中

(6)

将其定义为判断矩阵的特征值。RI为平均随机一致性指标,其取值与矩阵阶数有关。通过比较CR的值是否满足要求(即CR<0.1)来判断所选判断矩阵是否合理。

(4) 层次总排序与检验。总排序是指元素在顶层的相对权重,采用从上而下的方法逐层合成。设第k层n个元素对于k-1第j个元素的单排序权重Ωj(k)=[ω1j(k)ω2j(k)…ωnj(k)]T,不受j支配的元素的权重为0。令Ω(k)=[ω1(k)ω2(k)…ωn(k)]T表示第k层元素对顶层元素的排序,则第k层元素对于总目标的总排序满足:

(7)

2　培养水平评价模型的构建

2.1复合型工程科技人才培养水平评价层次

为了使复合型工程科技人才培养模型规范有效,本文参考美国人才培养的创新模式[8],并结合复合型人才培养模式的研究经验,对复合型工程科技人才培养进行层次分析。为了客观地反映学生理论知识、职业素质及实践能力的真实情况,本文设定了复合型工程科技人才培养水平评价层次，主要包括管理体系、环境平台、教学模式、实践应用及培养效果等5个层面，在这5个层面都有各自方面的因素,管理体系中分为领导体制、培养政策、培养管理制度及激励机制4个方面;环境平台下分为教风和学风建设、学术交流平台及学术型社团创办3个方面;教学模式分为教学理念、教学内容、教学方法、复合课程设置及考核机制5个方面;实践应用分为课外科技活动、社会科技实践及参与科研项目3个方面;培养效果分为社会服务、经济效益、科技成果3个方面。

2.2复合型工程科技人才培养水平评价模型

复合型人才培养水平评价模型指标的确定是构建复合型人才培养指标体系的关键,本文将建立复合型工程科技人才培养水平评价模型如下:

(1) 确定评价指标。将复合型工程科技人才培养评价体系分为3层，分别为：顶层为目标层(A),即复合型工程科技人才培养评价指标体系;中间层为准则层(B),包括管理体系、环境平台和教学模式等;底层为方案层(C),包括领导体制、培养政策和培养管理制度等。

根据(1)式列出3层函数的关系如下:

(8)

其中，B1=G(C11,C12,C13,C14);B2=G(C21,C22,C23);B3=G(C31,C32,C33,C34,C35);B4=G(C41,C42,C43);B5=G(C51,C52,C53)。

即A层下面分为5个B准则,B1准则有4个C1方案组成,B1准则的方案与B2准则的方案是相互独立关系。

(2) 确定层次之间的判断矩阵。为获得准确的判断矩阵,对熟悉教学或管理的领导、老师做出了关于重要度的问卷调查。

根据专家填写的问卷表列出对应的判断矩阵表格,首先对每个专家的判断进行评价,根据某专家给出的A=F(B)、B1=F(C)的表格列出判断矩阵，见表2、表3所列。剔除有明显不合实际甚至偏激的表格,然后根据余下可信的表格综合计算排序向量。

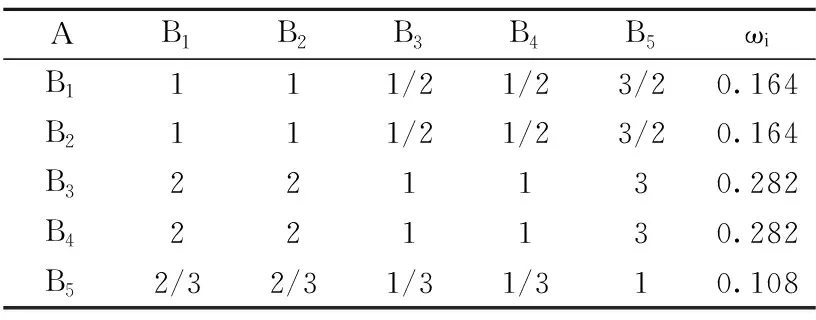
表2　判断矩阵(目标层A)

表3　判断矩阵(准则层B1)

根据(2)式将判断矩阵行元素(即每行全部内积值)相乘,得到表2中X1=3/8，X2=3/8，X3=12，X4=12，X5=4/81；同理得，表3中X1=1/24，X2=2/3，X3=32/3，X4=27/8。

根据(3)式计算权重,得到表2中权重向量为Ω=[0.1640.1640.2820.2820.108]T；同理得表3中权重向量为Ω=[0.100 50.200 10.399 80.299 6]T。

(3) 层次单排序与一致性检验。根据(4)～(6)式求得。表2中λmax=5.034，CI=0.007 5，CR=0.006 7。同理得表3中λmax=4.001，CI=0.000 5，CR=0.000 7。

由于CR<0.1,故判断矩阵选取合适,可以进一步用来构造总体模型。

(4) 层次总排序与检验。根据(7)式求B1准则层对应的方案层C11、C12、C13、C14，目标总排序分别为:

0.164×0.100 5=0.016，

0.164×0.200 1=0.033，

0.282×0.399 8=0.066，

0.108×0.299 6=0.049。

按照上述要求继续构造B2、B3、B4、B5的判断矩阵并计算权重检验合理性,求得方案层(C)每个元素相对目标层(A)的权重,得到复合型工程科技人才培养评价指标体系模型见表4所列。

表4　复合型工程科技人才培养评价指标体系

3　建模结果分析

根据本文构建的复合型工程科技人才培养水平模型可知,在B层中教学模式所占权重最多为0.282,实践应用与教学模式权重相当,这与在构建模型时给出的函数关系一致;B层5个元素的重要度扇形图如图1所示。

图1　B层次元素重要度扇形图

对于C层,管理体系中领导体制的权重最小为0.016,表示可以适当减少领导体制;在环境平台中应注重学术交流平台,因为其所占权重较高为0.082; 教学模式中复合课程权重为0.057,仅次于教学内容权重0.085,这与培养复合型人才的最终目标相统一;实践应用3个方案权重值一样,重要程度相同;培养效果占的总排序为0.108,经济效益和社会服务及科技成果同等重要。

此外，从B层“实践应用”对应的C层指标分析可知,课外科技活动、社会科技实践、参与科研项目权重最大,因此这3个方面在培养复合型人才时需要着重实施;教学内容、学术交流平台权重次之,说明这2个方面要侧重要求;师资力量、培养管理制度及复合课程设置权重也不低,表明这3个方面也要重点要求。

4　结　　论

本文通过AHP建立了一种复合型工程科技人才培养的评价体系模型,把AHP对直观模糊问题定性与定量分析这一优点充分应用到评价人才培养体系的模型中。提出重要度内积这一概念,定义直观的2个元素之间的重要度比值。将复合型工程科技人才培养的评价体系模型分为管理体系、环境平台、教学模式、实践应用、培养效果等准则,通过构建判断矩阵并对其进行逻辑合理性判断,验证得出该方法所构造的模型是符合逻辑准则的,可以作为评价复合型科技人才培养体系的依据。

[1]孙明保,李新平.基于层次分析法的人才培养质量评价指标体系及模型构建：以地方院校师范类人才培养为例[J].湖南理工学院学报(自然科学版)，2011，24(2):27-30.

[2]王新民,康虔,秦健春,等.层次分析法-可拓学模型在岩质边坡稳定性安全评价中的应用[J].中南大学学报(自然科学版),2013,44(6):2455-2462.

[3]李新,石建屏,曹洪.基于指标体系和层次分析法的洱海流域水环境承载力动态研究[J].环境科学学报,2011,31(6):1338-1344.

[4]吴大亲,么文学.基于层次分析法的应用型人才培养评价模式研究[J].长春师范学院学报(自然科学版),2010,29(4):28-30.

[5]寿志勤,陶建平,周健,等.基于可拓层次分析法的校园网络安全评估指标体系研究[J].合肥工业大学学报(自然科学版),2010,33(11):1643-1647.

[6]郭金玉,张忠彬,孙庆云.层次分析法的研究与应用[J].中国安全科学学报,2008,18(5):148-153.

[7]矫永康,李小民,毛琼.改进模糊层次分析法在虚拟维修训练评估中的应用[J].计算机工程,2014,40(10):314-317.

[8]李祖超,别雪君.美国高校拔尖创新人才培养模式评析[J].中国高等教育,2011(18):58-59.

(责任编辑万伦来)

Studyofevaluationsystemmodelofcompoundengineeringscienceandtechnologytalentstraining

ZHANG LI1, XU JUAN2， LU GEGE1， HUANG JINGRONG3

(1.SchoolofMachineryandAutomobileEngineering,HefeiUniversityofTechnology,Hefei230009,China； 2.SchoolofComputerandInformation,HefeiUniversityofTechnology,Hefei230009,China； 3.SchoolofInnovation,HefeiUniversityofTechnology,Hefei230009,China)

Compoundtalentstrainingevaluationsystemhasaguidingeffectonthechoiceoftrainingmechanismforcollegesanduniversities.Takingtheadvantagesofanalyticalhierarchyprocess(AHP)onmakingpolicyonvagueissuesinqualitativeandquantitativeways,theconceptoftheinnerproductofimportancedegreeisproposedtodescribetheimportantdegreeofratiobetweentwoelements.Theimportanceweightbasedonmanagementsystem,environmentplatform,teachingmode,practiceandapplicationandtrainingeffectisconstructed.Theevaluationindexsystemmodelofthetrainingofcompoundtalentsinengineeringscienceandtechnologyisestablished,andtheconsistencytestisconductedbyconstructingjudgementmatrixtoverifytherationalityofthemodel.Thestudyprovidesareferencefortheevaluationofcompoundtalentstrainingincollegesanduniversities.

analyticalhierarchyprocess(AHP);judgementmatrix;weight;evaluationindexsystem;innerproductofimportancedegree

2015-03-30；

2015-05-04

安徽省自然科学基金资助项目(1408085QE99);国家国际科技合作专项资助项目(2012DFB10060)和教育部工程科技人才培养专项研究资助项目(12JDGC007)

张利(1955-),女,安徽蚌埠人,合肥工业大学教授,硕士生导师.

10.3969/j.issn.1003-5060.2016.08.026

G420

A

1003-5060(2016)08-1138-04