带形状参数的二次非均匀双曲B样条曲线
2016-09-22王旭辉
方 玲, 王旭辉
(合肥工业大学 数学学院,安徽 合肥 230009)
带形状参数的二次非均匀双曲B样条曲线
方玲,王旭辉
(合肥工业大学 数学学院,安徽 合肥230009)
文章给出了带形状参数λ的二次非均匀双曲B样条曲线,可以通过改变λ值来调节曲线形状,从而为曲线表示提供了一种新方法。此外,该曲线不仅具有一般多项式B样条曲线的诸多优良性质,还可以精确地表示双曲线。文章给出具体例子说明通过改变λ的值来反映其对图形的影响。
双曲B样条;形状参数;非均匀节点;调节
0 引 言
B样条是一种通过基函数的线性组合表示的特殊样条曲线。B样条曲线在CAD、CAGD中被广泛应用。为了调整B样条曲线的形状,可以通过调节其控制顶点或改变其节点向量来完成,但这2种方法都有一定的局限性,如调节其控制顶点需要重新计算曲线方程,改变节点向量没有一定的规则。为了完善这些不足,人们研究了其他形式的样条曲线。例如,有理B样条曲线、三角多项式曲线[1-8]、双曲样条曲线[9-17],但是由于之前研究的曲线通过权因子的变化来调整曲线的形状或改变曲线的位置在计算方面(如求导、求积等)比较麻烦。为了增加对样条曲线的控制性,文献[11-15]研究了带形状参数的样条曲线,可以更加方便有效地对曲线形状进行调控。虽然二次非均匀B样条曲线的结构比较简单,但是它广泛应用于曲线曲面造型。
本文通过增加形状参数,给出了一种带一个形状参数的双曲B样条曲线的构造方法,不仅保持了双曲样条的连续性、几何不变性等很多优良性质,而且可以通过改变形状参数得到不同形状的曲线,达到调控曲线形状的效果。更重要的是该曲线能精确表示某些圆锥曲线和超越曲线。文献[3-8]中提出的方法能够精确表示椭圆,但不能精确表示双曲线,本文的方法能够精确地表示双曲线,补充了上述文献中提出的方法的不足。与文献[14]相比,在能够达到同样的目的下,本文构造的基函数形式更简洁、更易于应用。另外,相比于多参数的方法,在精确表示双曲线方面,单参数的方法更易于计算参数与调控。
1 二次双曲B样条的基函数
1.1基函数的构造
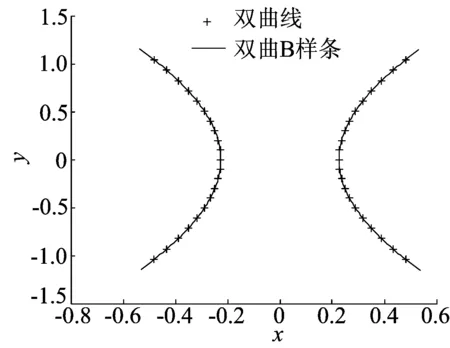
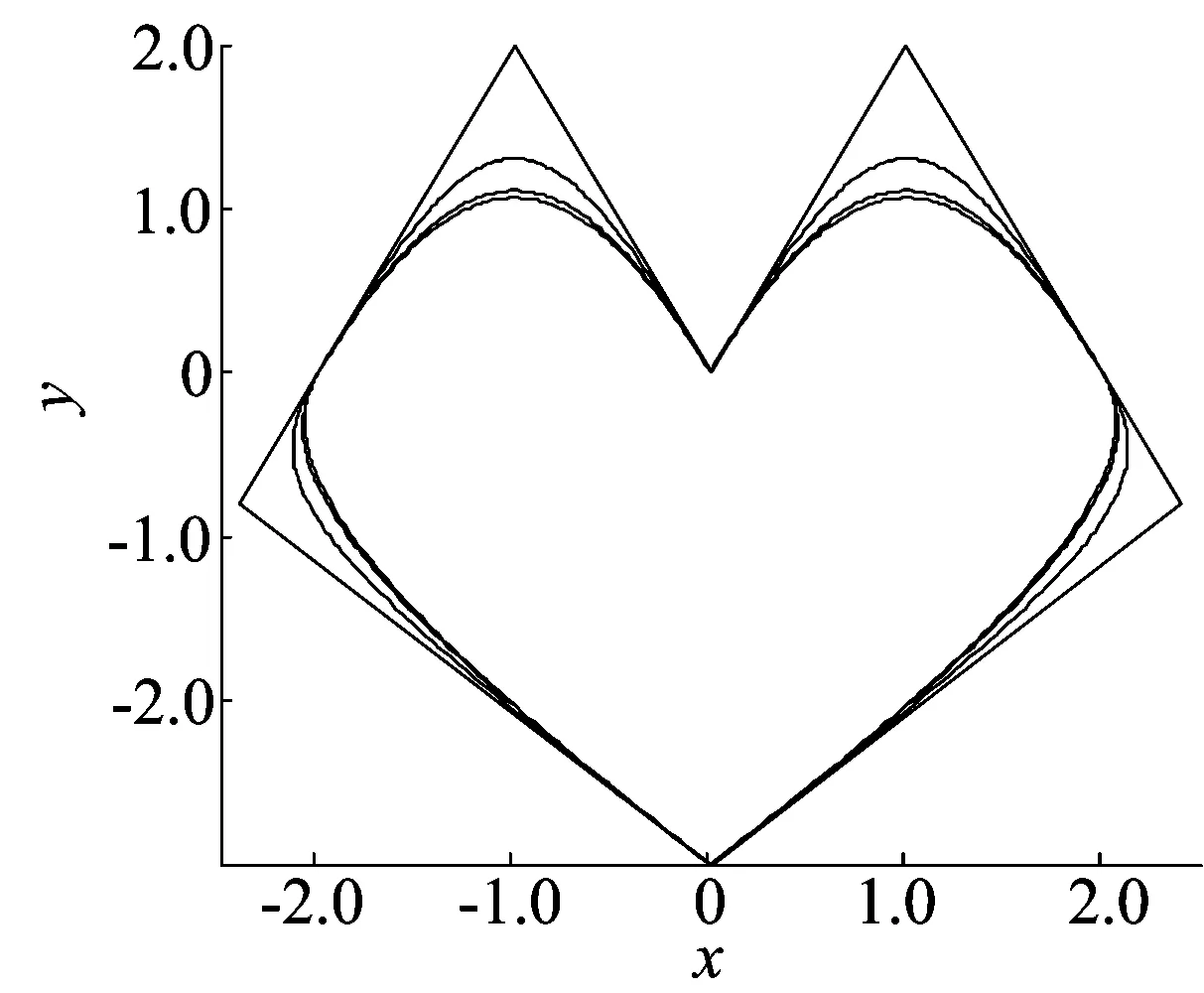
定义1对于任意给定的节点u0 称 (1) 为第i个带形状参数λ的二次非均匀双曲B样条基函数,简称二次双曲B样条基函数。当取均匀节点向量时,称(1)式为第i个带形状参数λ的二次均匀双曲B样条基函数。 经验证,若节点是均匀的,当λ=0时,(1)式定义的基函数为文献[9]中当α=1时的二次均匀双曲B样条基函数。 1.2基函数的性质 定理1通过(1)式所定义的基函数具有以下性质: (1) 局部支撑性。当ui 证明证明如下: (1) 当ui 1-cosh1<0, 所以有: 即 即 当ui 当ui+1 因为 所以 即0<1-βi+1ci+1-αi+1di+1<1。 当ui+2 1.3基函数的连续性 定理2设节点u0,u1,…,un+3满足u0 证明因为 所以 故(1)式定义的基函数bi(u)可以通过调节形状参数λ来改变基函数,如图1所示。 图1 形状参数λ的变化对基函数的影响 1.4重节点的情形 当双曲B样条基函数的节点重数k≤3时,只要把对应的区间缩小为0,并去掉基函数的相应段即可。特别地,当ui+1=ui+2时,Δui+1=0,(1)式变为: (2) 定理3若u=uj(j=i,i+1,i+2,i+3)是基函数bi(u)的k (k=2,3)重节点,则基函数的支撑区间从3段减少为4-k段。对均匀节点,当k=2时,基函数在uj上连续;当k=3时,基函数不连续。对非均匀节点,基函数不连续。 节点u2=3为2重节点,其余节点分别为单节点且等距或不等距时的基函数如图2所示。 图2 节点u2=3为2重节点,其余节点为单节点的基函数 从图2可以看出,除重节点外,若其余节点为单重且等距,则基函数是连续的;若其余节点为单重且不等距,则基函数不连续。 利用定义1的基函数(1),可以定义如下的二次双曲B样条曲线。 定义2任意给定R2或R3中控制顶点P0,P1,…,Pn(n≥2),节点 u0,u1,…,un+3及形状参数0≤λ<2e/(e2-1),则 (3) 称(3)式为单形状参数的二次非均匀双曲B样条曲线,其中bi(u)为(1)式所定义的基函数。 当ui (4) 2.1曲线的连续性 定理4给定节点u0,u1,…,un+3,当u=ui为单节点时,(3)式定义的曲线在该点为C1连续;当u=ui为k重节点时,(3)式定义的曲线在该点为C2-k连续(k=2,3)。 2.2曲线的整体调控性 给定样条曲线的控制顶点,其对应的二次样条调控性可分为: (1) 固定节点,通过改变λ的值来进行调控,如图3a所示。 (2) 固定λ,通过改变节点来进行调控,如图3b所示。 (a) 改变λ (b) 改变节点向量 2.3精确表示双曲线 定理5二次样条曲线(3)式可精确表示双曲线。 证明令之前所定义的双曲B样条曲线中的λ=0,控制顶点为Pi=(xi,yi),i=0,1,2,且x2=x0≠0,y2=-y0≠0,x1=y1=0,则有: (5) 则有: (6) 易知(6)式可精确表示双曲线,如图4所示。 图4 精确表示的双曲线 2.4图形例子 通过改变二次双曲B样条的形状参数λ值得到的一系列图形如图5所示。 (a) 花瓣 (b) 心形 本文构造了带一个形状参数的二次双曲B样条曲线,其形式比较简单,具有二次B样条曲线的连续性、权性等性质,并且能够整体调控曲线,能精确表示双曲线,能近似表示圆与椭圆。当控制多边形和节点向量确定时,可以通过改变形状参数的大小来调整曲线的形状,从而获得需要的形状。 [1]LUYG,WANGGZ,YANGXN.UniformtrigonometricpolynomialB-spline[J].ScienceinChina,2002,45(5):335-343. [2]HANXL.Quadraticpolynomialcurveswithashapeparameter[J].ComputerAidedGeometricDesign,2002,19(7):503-512. [3]吴晓勤,韩旭里.带参数的二次三角多项式样条曲线[J].工程图学学报,2006,27(1):92-97. [4]邬弘毅,陈晓彦.多形状参数的三次非均匀三角多项式曲线[J].计算机辅助设计与图形学报,2006,18(10):1599-1606. [5]谢进,邬弘毅,邓四清,等.多形状参数的二次非均匀三角多项式曲线[J].工程图学学报,2007,28(5):49-55. [6]余俊.带多个形状参数的三次三角多项式样条曲线[J].佳木斯大学学报(自然科学版),2010,28(2):291-295. [7]李军成,杨炼.带形状参数的C2连续类三次三角样条曲线[J].计算机工程与应用,2012,48(30):201-204. [8]李明珠,陈丽娟.带形状参数的二次三角多项式曲线[J].高等学校计算数学学报,2013,35(4):289-294. [9]LUYG,WANGGZ,YANGXN.UniformhyperbolicpolynomialB-splinecurves[J].ComputerAidedGeometricDesign,2002,19(6):379-393. [10]QIANJ,TANGYH.OnNon-uniformalgebraic-hyperbolic(NUAH)B-spline[J].NumericalMathematics,2006,15(4):320-335. [11]王文涛,汪国昭.带形状参数的双曲多项式均匀B样条[J].软件学报,2005,16(4):625-633. [12]钱天胜,黄有度,尹池江.多形状参数的双曲多项式均匀B样条[J].合肥工业大学学报(自然科学版),2011,34(8):1276-1280. [13]韩敬利,董会,王兆丽.三次带多形状参数双曲均匀B样条曲线[J].科学技术与工程,2011,11(26):6471-6473. [14]陆利正,汪国昭.二次带形状参数双曲B样条曲线[J].高校应用数学学报,2008,23(1):105-111. [15]谢进,檀结庆.多形状参数的二次双曲多项式曲线[J].中国图象图形学报,2009,14(6):1206-1211. [16]谢进,檀结庆,李声锋,等.非均匀的二次三角双曲加权样条曲线[J].计算数学,2010,32(2):147-156. [17]谢进,檀结庆,李声锋.含有权参数的二次代数双曲B样条曲线[J].高等学校计算数学学报,2011,33(4):337-346. (责任编辑朱晓临) Quadraticnon-uniformhyperbolicB-splinecurveswithashapeparameter FANGLing,WANGXuhui (SchoolofMathematics,HefeiUniversityofTechnology,Hefei230009,China) Akindofquadraticnon-uniformhyperbolicB-splinecurvewithashapeparameterλispresented.Theshapeofthecurvecanbemanipulatedbychangingthevalueoftheparameterλ,thusconstructingasimplemethodtorepresentplanarcurves.ThiskindofcurvenotonlypossessesthemostadvantagesofquadraticpolynomialB-splinecurves,butalsorepresentshyperbolasaccurately.Thenumericalexamplesaregiventodemonstratetheeffectoftheparameterλonthegraphbychangingthevalueofit. hyperbolicB-spline;shapeparameter;non-uniformknot;regulation 2015-03-30; 2015-08-14 国家自然科学基金青年基金资助项目(11301131) 方玲(1989-),女,安徽安庆人,合肥工业大学硕士生; 王旭辉(1980-),男,安徽庐江人,博士,合肥工业大学副教授,硕士生导师. 10.3969/j.issn.1003-5060.2016.08.028 TP391 A 1003-5060(2016)08-1148-05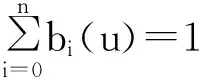




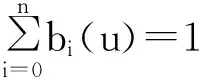



2 二次双曲B样条曲线




3 结 论
