一种稀疏度自适应的压缩感知信道估计算法

林思铭,　彭卫东,　李明阳,　林志国,　李　瑞



一种稀疏度自适应的压缩感知信道估计算法

林思铭1,2,彭卫东2,李明阳3,林志国1,2,李瑞1,2

(1.空军工程大学 装备管理与安全工程学院,陕西 西安710051; 2.空军工程大学 装备发展与运用研究中心,陕西 西安710051; 3.中国人民解放军95972部队,甘肃 酒泉735018)

针对目前稀疏度自适应的压缩感知(compressed sensing,CS)信道估计算法计算量过大的问题,文章提出了基于关联度分析的稀疏度自适应归档正则化迭代硬阈值(sparsity adaptive archiving normalized iterative hard thresholding,SAANIHT)算法。ANIHT算法可以解决传统压缩感知理论计算量大、计算时间过长的问题,但需要预知信道的稀疏度。引入高斯核函数对一种稀疏度估计算法进行了改进,并与ANIHT算法结合,使其可以在盲稀疏情况下对信道进行估计。仿真结果表明,在同等稀疏度条件下,该算法比其他算法节约了计算时间,在低信噪比下性能更优,具有较好的重构性能与稳定性。

压缩感知;稀疏多径信道估计;归档正则化迭代硬阀值算法;高斯核函数;稀疏度自适应

压缩感知(compressed sensing,CS)理论被提出以来,已产生了大量的相关研究与应用。该理论主要涉及3个方面的内容,即信号的稀疏表示、观测矩阵的构建与重构算法[1-2]。信号能够被稀疏表示是压缩感知的前提,如果信号在某个变换基上是稀疏的,设计一个与变换基不相关的观测矩阵对信号进行观测,从观测集合中可以重构出原始稀疏信号。

在无线通信中,准确的信道估计是通信系统的信号检测、均衡等步骤的基础和关键。已有的信道估计算法分为基于导频或训练序列的估计算法和盲估计算法,前者主要包括最小二乘(least square,LS)估计算法,但需要较大的导频开销,而后者不适用于较低信噪比情况。已有研究表明,无线多径信道具有稀疏特性[3-4],利用压缩感知只需要较少的参考信号即可恢复信道的状态信息,相对于最小二乘法等传统信道估计方法大大节省了导频开销与计算时间。测量矩阵通常由训练序列构成,研究主要集中在重构算法方面,主流算法包括基于贪婪算法的匹配追踪(matching pursuit,MP)算法及正交匹配追踪(compressive sampling matching pursuit,CoSaMP)算法[5-6]等,其中CoSaMP算法的导频开销更小,性能较优。但上述算法存在计算量较大的问题,迭代硬阈值(iterate hard thresholding,IHT)[7]算法复杂度较低,已有研究者改进了其收敛速度慢的缺点[8-10]。

上述重构算法在计算时,需要信道的稀疏度信息,而接收机并不能获知信道稀疏度信息。稀疏度自适应匹配追踪算法(sparsity adaptive matching pursuit,SAMP)[11]不需要预知信号稀疏度,但存在运算速度过慢和过估计的问题。针对稀疏度未知信道,本文结合阈值迭代算法、测量向量的关联分析理论和回溯迭代的思想,提出一种稀疏度自适应的归档正则化迭代硬阈值(sparsity adaptive archiving normalized iterative hard thresholding,SAANIHT)算法,解决了自适应中的欠估计与过估计问题。实验仿真表明,本文提出的算法比SAMP和其他稀疏度自适应算法运算时间缩短,在低信噪比下具有较优的重构性能与稳定性。

1　基于压缩感知的信道估计模型

一般的无线信道可以等效为线性、时变系统,传输模型可以表示为:

(1)

其中,y(t)为接收信号;X(f)为发送信号的傅里叶变换;H(t,f)为信道的时变频率响应;n(t)为服从N(0,σ2)的高斯白噪声。若在一个符号周期内,信道的冲激响应是不变的,冲激响应系数则可以简化为一个长度为N的复增益系数h(i)=aie-jθi(i=0,1,2,…,N-1)。

在导频辅助的信道估计中,训练序列的符号可以表示为x(i)(i=1,…,p),其中p为训练符号的长度,在接收端,采样符号表示为y(j)(j=1,…,N+p-1),则有:

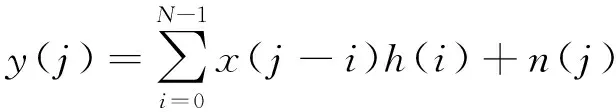
(2)

假设P为训练序列组成的(N+M-1)×N维的Toeplitz矩阵,对于传统的信道估计算法,最小二乘法的信道估计输出hLS=(PHP)-1PHy,但该方法对导频长度要求较高,且抗噪性能很差;最小均方误差估计算法设计了自相关矩阵Rhh，估计值hLMMSE=Rhh[Rhh+σ2(XXH)-1]-1hLS,精确性优于最小二乘法,但涉及大量矩阵的逆运算,计算复杂度高,不适合工程应用。而在基于压缩感知的信道估计中,(2)式可以直接简化为:

(3)

即通信系统的传输模型可以表示为:

y=Xh+n

(4)

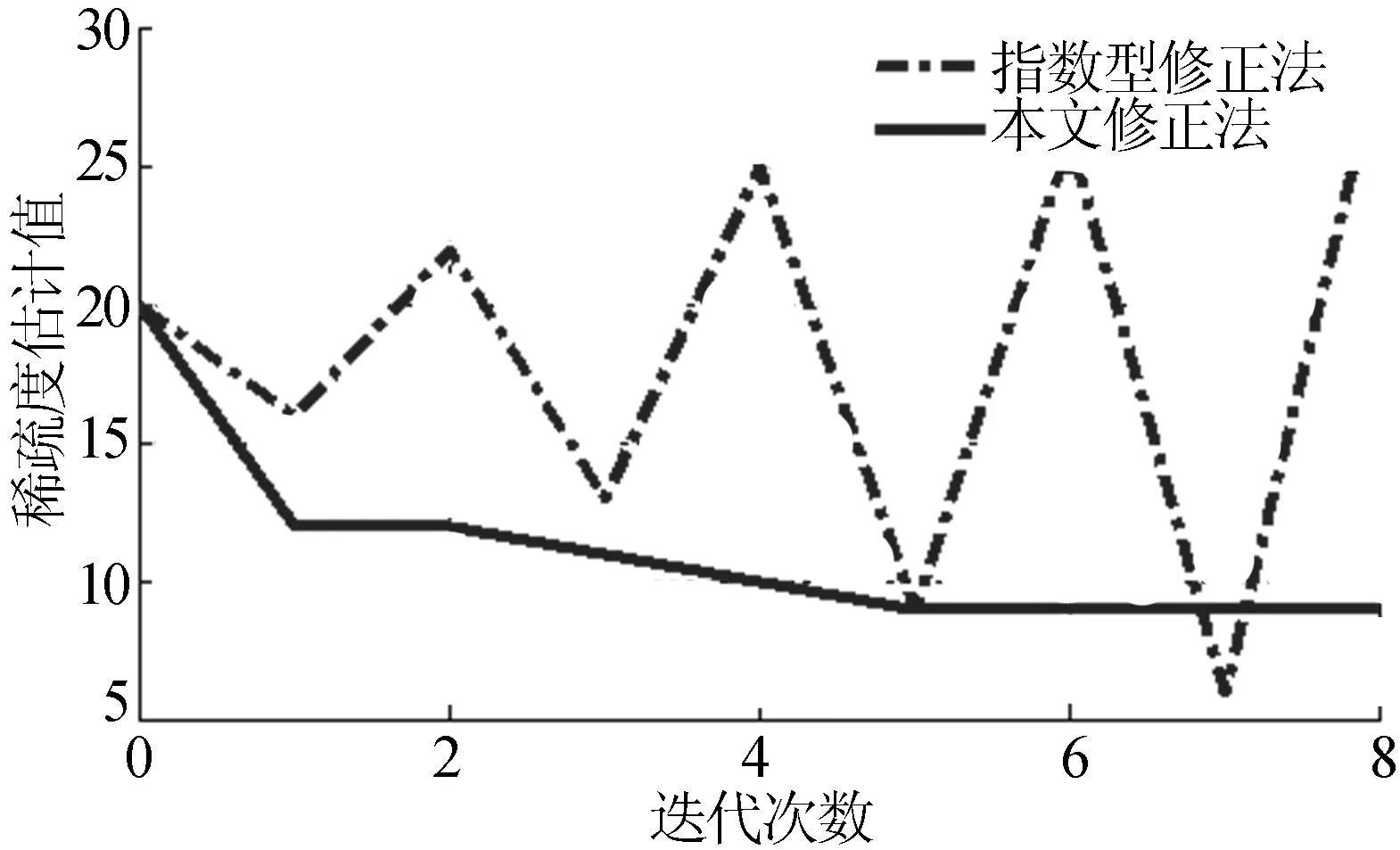
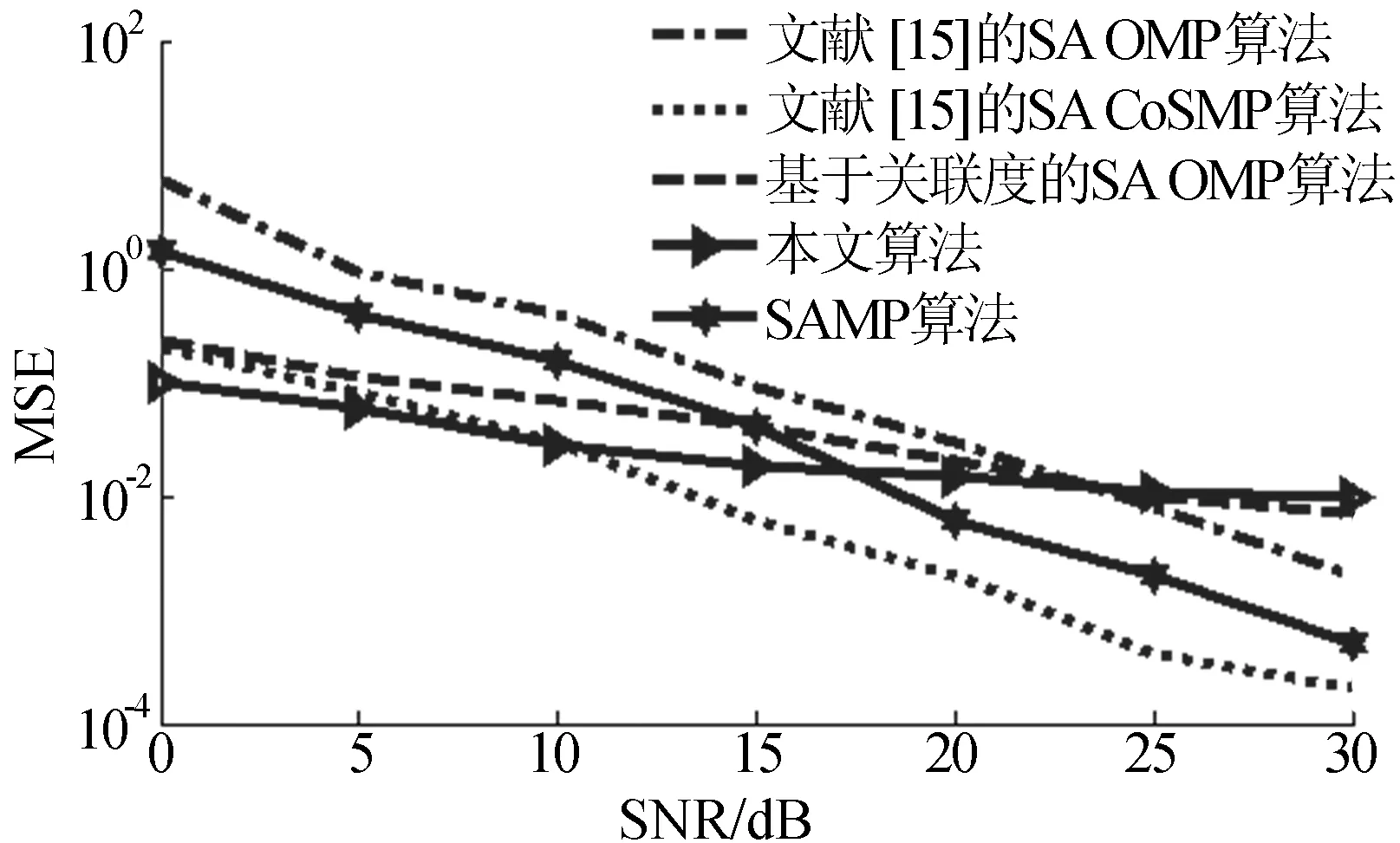
其中，X为具有Toeplitz结构的M×N(M

min‖h‖1,

(5)

其中,ε为噪声能量。

PN(pseudo-noise sequence)序列作为信道估计训练序列时,重构性能比其他构造方法更加优异。本文选取PN序列循环移位生成的优化观测矩阵作为观测矩阵X。文献[8]已证明，对于该矩阵X，始终存在δk∈[0,1-1/n)∈[0,1)，使之满足RIP特性,为估计算法的重构精度提供了保证。

2　信道估计算法

2.1稀疏度自适应算法

压缩感知的传统重构算法不适用于稀疏度未知的情况,针对这一问题,文献[11]提出的SAMP算法是利用分段思想实现信号重构,虽然估计精确度较高,但迭代次数很大,非常费时;文献[13]采用原子匹配测试的方法,提出了一种改进的MSAMP算法;文献[14]根据相邻信号能量差的变化规律,提出了对数型“变步长”的双阈值估计法。这些算法都一定程度上优化了SAMP算法,但没有跳出原有框架,收敛速度的提升有限。文献[15]运用小波分析的方法,将稀疏度估计与重构过程分开,减少了收敛时间,对算法研究具有启发意义。

已有的重构迭代方式基本都是通过迭代计算找出合适的原子组成支撑集,进而重构原始信号。借鉴信号重构的思想,使用测量向量与测量矩阵的关联度信息来获得稀疏度的粗略估计[16],定义接收信号与观测矩阵的关联性,即

C=XTy

(6)

其中,C为关联向量;XT为观测矩阵的转置。

C的物理意义在于每个元素的值表示了测量矩阵中的每个列向量与接收信号的关联度大小。定义“有效原子”为测量矩阵中与信道系数非0向量的对应列,其与测量向量的关联度高于其他“未激活原子”。在理想情况下,采用该方法分析长度为64、稀疏度分别为2、4、8、16的稀疏信道,得到关联向量的二阶差分幅值降序,如图1所示。

图1　关联向量的二阶差分幅值降序排列

图1中,幅值为关联向量的系数模值,单位为1。由图1可以看出,在基于关联度分析的方法中,幅值在真实稀疏度附近会有一定程度的突降,因此该方法可以大致估计信道稀疏度,但在稀疏度较高时准确性会受到一定的影响。基于关联度分析理论,定义稀疏度估计式[16]为:

(7)

其中,D为关联向量C各元素降序排列的二阶差分向量;L为信道长度;ρ为阈值系数,ρ∈[1,10)。在实际应用中,ρ的取值依赖经验,取值过大,容易造成稀疏度粗估计过小,若粗估计值过小,将很难对其进行修正,但是,若信道稀疏度很低,需要取很大的ρ值才能让稀疏度尽快收敛;同时,由于无线信道的时变特性,很难找到能够对应多种情况的ρ值。因此,需要对其进行改进。

高斯核的定义是信号距离的平均值,近似高斯核变换可以去除无关信息[17],获取冗余信息来作为稀疏度粗估计的外部信息。通过将接收信号和关联向量的差放大，高斯核函数的图形可以在一定程度上反映出稀疏情况。本文引入高斯核函数,定义基于高斯核函数的稀疏度估计表达式为:

(8)

其中,η为估计系数,初始值一般设为2。高斯核函数值与最大二阶差分值的乘积能够在一定程度上反映信道状况,与(7)式相比不需要依赖经验,对实际应用具有一定的价值。

当粗估计稀疏度后,若信号重构的信号残差超出容忍度,需要对稀疏度进行修正,定义稀疏度修正表达式为:

(9)

不同于已有的指数型修正方法,本文选用二阶差分向量中的从Kn到L-2位数据对稀疏度进行修正,从而可以避免指数型修正方法在多次迭代后使重构算法陷入死循环;但本文的办法可能导致在一定修正次数后,恒等于某一个远小于稀疏度的值。为了解决这一问题,设置当Kn+1=Kn时,令η=η+1,采用(9)式对稀疏度进行修正。设置信道稀疏度为8,当稀疏度粗估计值为20,分别采用2种方式对稀疏度进行修正,结果如图2所示。

图2　2种稀疏度修正方式对比

由图2可以看出,在粗估计值相对实际稀疏度较大的情况下,本文方法对稀疏度的逼近更快,而且避免了指数型修正方式的稀疏度震荡问题;另一方面,从算法复杂度来看,本文算法仅涉及1次指数运算,而指数型修正法每次都要调用指数运算,算法复杂度高出了1个数量级。

2.2稀疏度自适应信道估计算法实现

由于信道估计中的观测矩阵满足RIP性质,线性规划算法和贪婪算法都能精确估计信道系数。凸优化算法不适合求解大规模信号,且可能产生能量搬移问题。贪婪算法计算时间过长,且性能受限于稀疏度大小。IHT算法对应求解l0问题,通过直接计算稀疏信号的非零元个数,寻找逼近度最高的K项支撑[8],文献[10]对IHT算法提出了改进,构造了NIHT算法,该尺度因子对NIHT算法进行了较大简化。文献[8]结合了NIHT与BIHT算法[9-10],利用外部归档引入精英策略设计了ANIHT算法,该算法比原有算法收敛速度更快,在低信噪比下重构精度和稳定性更高,而且配合由PN序列组成的观测矩阵,可以将算法中的乘积运算简化为加减运算,降低了硬件的资源占用,具有较高的工程应用价值。

结合改进的稀疏度估计和信号重构算法,本文给出改进算法的具体步骤,称为基于关联度分析的归档正则化迭代硬阀值算法。

稀疏度估计的具体步骤如下:

(1) 对于接收信号,计算关联向量C=XTy。

(2) 计算C的二阶差分值,得到二阶差分向量D=diff2(C),并将各元素按幅值降序排列。

(3) 粗略估计稀疏度,即

信道重构的具体步骤如下:

(1) 令r0=y,h0=0,μ0=1,a0=1。

(2) 如果ai>hi+μiXTri,则

ai=hi+μiXTri;

(3) 如果|hi-hi-1|l∞≤ε,迭代结束。否则,若k

(4) 输出信道系数的估计值h。

3　仿真与性能分析

本文在Matlab平台上进行仿真验证,仿真采用OFDM信道模型,发送的信号功率为1,设置信道长度为64,稀疏度为8,误差容忍度为10-2,训练序列为长度64的PN序列,在信噪比(signal noise ratio,SNR)为10 dB下进行仿真,本文方法的估计结果如图3所示。

图3　估计性能

由图3可知,通过设置适当的误差容忍度,本文方法可以高概率地重构真实多径,由于噪声影响,个别径上的信道系数估计存在一定误差,但这种误差会随着信噪比的增大而可以忽略不计。

对本文算法在不同信噪比下的估计性能进行仿真,并与SAMP算法和文献[15]提出的算法进行对比,设置信道条件不变,将信噪比范围改为0～30 dB,对不同算法分别进行100次MonteCarlo仿真。不同算法的均方误差(mean squared error,MSE)性能曲线如图4所示。

图4　不同算法的性能比较

由图4可以看出,随着信噪比的增加,不同算法信道估计的均方误差都不断下降。由于ANIHT算法在缩短收敛时间时牺牲了重构精度,加上算法设计原理不同,精度的提升速度较其他算法稍慢;但在低信噪比下,本文算法相对于其他算法具有更优性能,更适合工程实际应用。

在实际工程应用中,对于压缩感知的信道估计算法,不仅需要其重构算法具有较高的重构精确度,还由于无线信道的快速时变特性,需要算法具有较低的运行收敛时间。测试使用的计算机配置为Pentium(R)Dual-Core 2.5 GHz,2.5 GHz搭载2 G内存,其他条件与上文相同。本文提出的算法与其他算法的运行收敛时间见表1所列。由表1可知,与其他稀疏度自适应的信道估计算法相比,本文算法减少了计算量,收敛时间较短。

表1　不同算法的计算时间对比　s

4　结　　论

本文提出了一种稀疏度自适应的压缩感知无线信道估计算法SAANIHT,该算法分为2步,即稀疏度粗估计和信道重构与稀疏度修正。仿真结果表明,相比于其他算法,本文算法的性能更优、计算量更小、收敛速度更快,具有一定的应用价值。

[1]BARANIUK R G.Compressive sensing[J].IEEE Signal Processing Magazine,2007,24(4):118-121.

[2]CANDES E J,WAKIN M B.An introduction to compressive sampling[J].IEEE Signal Processing Magazine,2008,25(2):21-30.

[3]COTTER S F,RAO B D.Sparse channel estimation via matching pursuit with application to equalization[J].IEEE Transactions on Communications,2002,50(3):374-377.

[4]EDFORS O,SANDELL M,VAN DE Beek J J,et al.OFDM channel estimation by singular value decomposition[J].IEEE Transactions on Communications,1998,46(7):931-939.

[5]MALLAT S G,ZHANG Zhifeng.Matching pursuits with time-frequency dictionaries[J].IEEE Transactions on Signal Processing,1994,41(12):3397-3415.

[6]TROPP J A,GILBERT A C.Signal recovery from random measurements via orthogonal matching pursuit[J].IEEE Transactions on Information Theory,2008,53(12):4655-4666.

[7]BLUMENSATH T,DAVIES M E.Iterative hard thresholding for compressed sensing[J].Applied and Computational Harmonic Analysis,2009,27(3):265-274.

[8]李明阳,柏鹏,王徐华,等.基于压缩感知的稀疏多径信道估计[J].系统工程与电子技术,2013,35(5):909-913.

[9]杨海蓉,方红,张成,等.基于回溯的迭代硬阈值算法[J].自动化学报,2011,37(3):276-282.

[10] BLUMENSATH T,DAVIES M E.Normalized iterative hard thresholding:guaranteed stability and performance[J].IEEE Journal of Selected Topics in Signal Processing,2010,4(2):298-309.

[11]DO T T,GAN L,NGUYEN N,et al.Sparsity adaptive matching pursuit algorithm for practical compressed sensing[C]//The 42nd Asilomar Conference on Signals,Systems and Computers.IEEE,2008:581-587.

[12]SEBERT F,ZOU Y M,YING L.Toeplitz block matrices in compressed sensing and their applications in imaging[C]//International Conference on Information Technology and Applications in Biomedicine.IEEE,2008:47-50.

[13]朱延万,赵拥军,孙兵.一种改进的稀疏度自适应匹配追踪算法[J].信号处理,2012,28(1):80-86.

[14]毕学霞,尚振宏,强振平,等.一种基于变步长的稀疏度自适应匹配追踪算法[J].系统仿真学报,2014,26(9):2116-2120,2125.

[15]周华,徐志京.一种基于CS理论的稀疏度自适应的水声信道估计方法[J].微型机与应用,2015,34(12):70-72.

[16]陈保豪.基于压缩感知的信道估计方法研究[D].北京:北京邮电大学,2014.

[17]ZHONG F,GUO S X,XU X.Joint channel coding based on LDPC codes with gaussian kernel reflecton and CS redundancy[J].Applied Mathematics and Information Sciences,2013,7(6):2421-2425.

[18]BAJWA W U,HAUPT J D,RAZ G M,et al.Compressed channel sensing[C]//42nd Annual Conference on Information Sciences and Systems.IEEE,2008:5-10.

(责任编辑胡亚敏)

A sparsity adaptive CS-based channel estimation algorithm

LIN Siming1,2,PENG Weidong2,LI Mingyang3,LIN Zhiguo1,2,LI Rui1,2

(1.College of Equipment Management and Safety Engineering,Air Force Engineering University, Xi’an 710051, China; 2. Research Center of Equipment Development and Application, Air Force Engineering University, Xi’an 710051, China; 3.Unit 95972 of PLA, Jiuquan 735018, China)

The traditional sparsity adaptive multipath channel estimation algorithms based on compressed sensing(CS) cost too much time. For solving this problem, a sparsity adaptive archiving normalized iterative hard thresholding(SAANIHT) algorithm based on correlation analysis is proposed. The ANIHT algorithm has fewer calculation amount than traditional algorithm only if the channel sparsity degree has been known. In order to make the algorithm possess the ability of blind sparse channel estimation, a sparsity adaptive method optimized by the Gaussian kernel function is introduced. The simulation results show that for the same sparsity degree, the proposed algorithm costs fewer time than other algorithms and has better performance in low signal-to-noise ratio and better convergence performance and stability.

compressed sensing(CS); sparse multipath channel estimation; archiving normalized iterative hard thresholding(ANIHT) algorithm; Gaussian kernel function; sparsity adaptive

2015-10-28；

2016-02-24

国家自然科学基金资助项目(6150051163)

林思铭(1992-),男,福建福州人,空军工程大学硕士生;

彭卫东(1968-),男,河北石家庄人,博士，空军工程大学教授,硕士生导师.

10.3969/j.issn.1003-5060.2016.08.010

TN911.5

A

1003-5060(2016)08-1055-05