影响装备状态的灰色关联度分析模型

安雨晨，王兴福，楚康帅，张新巍

(1.军事交通学院 综合训练基地，天津 300161； 2.军事交通学院 基础部，天津 300161)



影响装备状态的灰色关联度分析模型

安雨晨1，王兴福1，楚康帅1，张新巍2

(1.军事交通学院 综合训练基地，天津 300161； 2.军事交通学院 基础部，天津 300161)

为研究装备状态影响因素变化规律，分析影响装备状态(新、堪、待、废)因素的相关联性，根据部队部署、装备动态变化情况和部队装备状况等因素，在数据整合和分析的基础上，通过建立灰色关联度分析模型，研究解决影响装备状态的因素。模拟验证结果表明，该方法能够较真实地反映不同因素对装备的影响程度。

灰色关联度；关联性分析；装备状态

大数据作为生成新质战斗力的强力引擎，代表着军事技术和作战方式的发展趋势，是我军信息化建设的一个重要内容，对控制危机、遏制战争、打赢战争具有重要意义。目前，装备保障的稳定性和可靠性还不够高，精确化保障程度较低，依靠信息技术实现装备保障实时精确化还有一定差距，在该背景下，研究影响装备保障状态的相关因素，发现其中蕴含的内在规律，对建立保障资源信息库，提高装备保障稳定性和可靠性具有一定意义。本文通过建立灰色关联度[1]分析模型，研究影响装备状态的因素，该方法的核心是计算关联度。一般来说，关联度的计算首先要对原始数据进行处理，计算关联系数，由此就可计算出关联度。通过比较关联度的大小，可得出某一因素对装备状态的影响程度。

1　算法流程

1.1原始数据的处理

由于各因素有不同的计量单位，为便于分析比较，要对原始数据进行无量纲化处理，其方法包括标准化、均值化等。

(1)标准化。该方法处理后的各指标均值均为0，标准差均为1，它只反映了各指标之间的相互影响，在无量纲化的同时，也抹杀了各指标之间变异程度上的差异，因此，标准化方法并不适用于多指标综合评价。

(2)均值化。先分别求出各个原始数列的平均数，再用数列的所有数据除以该数列的平均数，就得到一个各个数据相对于其平均数的倍数数列，即均值化数列。均值化方法处理的各指标数据构成的协方差矩阵，既可以反映原始数据中各指标变异程度上的差异，也包含各指标相互影响程度差异的信息。

本文分析影响装备状态的因素涉及多个评价指标，且各指标间相互影响，因此选用均值化方法处理原始数据。

1.2关联系数的计算

选取所给数据其中一组为参考数列：

{x0(t)}={x01，x02，…，x0n}

(1)

与参考数列作关联程度[2]比较的p个数列(常称为比较数列)为

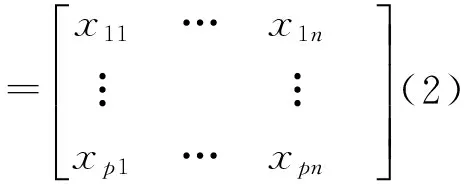
式中n为数列的数据长度，即数据的个数。

从几何角度看，关联程度实质上是参考数列与比较数列曲线形状的相似程度，可用曲线间的差值大小作为关联度的衡量标准。

将第k个比较数列(k=1,2,…,p)各期的数值与参考数列对应期的差值的绝对值记为

Δ0k(t)=|x0(t)-xk(t)|t=1，2，…，n

对于第k个比较数列，分别记Δ0k(t)中的最小数和最大数为Δ0k(min)和Δ0k(max)。对p个比较数列，又记p个Δ0k(min)中的最小者为Δ(min)，p个Δ0k(max)中的最大者为Δ(max)。这样Δ(min)和Δ(max)分别是所有p个比较数列在各期的绝对差值中的最小者和最大者。因此，第k个比较数列与参考数列在t时期的关联程度[3](常称为关联系数)的计算式为

(3)

式中ρ为分辨系数[4]，用来削弱Δ(max)过大而使关联系数失真的影响。

引入分辨系数是为了提高关联系数之间的差异显著性，0<ρ<1。应根据实际观测序列的具体情况动态取值：当观测序列出现奇异值时，ρ取较小值，以克服奇异值的支配；当观测序列比较平稳时，ρ取较大值，充分体现关联度的整体性。

可见，关联系数反映了两个数列在某一时期的紧密程度。例如，在Δok(t)=Δ(min)的时期，ξ0k(t)=1，关联系数最大；而在Δ0k(t)=Δ(max)的时期，关联系数最小。由此可知，关联系数变化范围为0<ξ0k(t)<1。

显然，当参考数列的长度为n时，由p个比较数列共可计算出n×p个关联系数。

1.3关联度的求解

由于每个比较数列与参考数列的关联程度是通过n个关联系数来反映的，关联信息分散，不便于从整体上进行比较。因此，有必要对关联信息作集中处理。而求平均值便是一种信息集中的方式。即用比较数列与参考数列各个时期的关联系数的平均值来定量反映比较数列与参考数列的关联程度，其计算公式为

(4)

式中rok为第k个比较数列与参考数列的关联度[5]。

不难看出，关联度与比较数列、参考数列及其长度有关。而且，原始数据的无量纲化方法和分辩系数的选取不同，关联度也会有变化。

1.4关联度的排序

由上述分析可见，关联度只是因素间关联性比较的量度，只能衡量因素间密切程度的相对大小，其数值的绝对大小常常意义不大，关键是反映各个比较数列与同一参考数列的关联度大小。当比较数列有p个时，相应的关联度就有p个。按其数值的大小顺序排列，便组成关联序。它反映了各比较数列对于同一参考数列的“主次”“优劣”关系。灰色关联度分析方法的运用之一就是因素分析。在系统发展过程中，若两个因素变化趋势具有一致性，即同步变化程度较高，即可认为二者关联较高，反之则较低，灰色关联度法对于一个系统发展变化态势提供了量化的度量，非常适合动态的历程分析。

2　算法实现

本文根据某一年在不同区域内(按经、纬度划分)，某部队装备的使用状况数据进行处理整合得到表1，其中，01为新品，02为堪用品，03为待修品，04为报废品。据此，按照以上模型进行关联度分析，验证该算法的可行性。

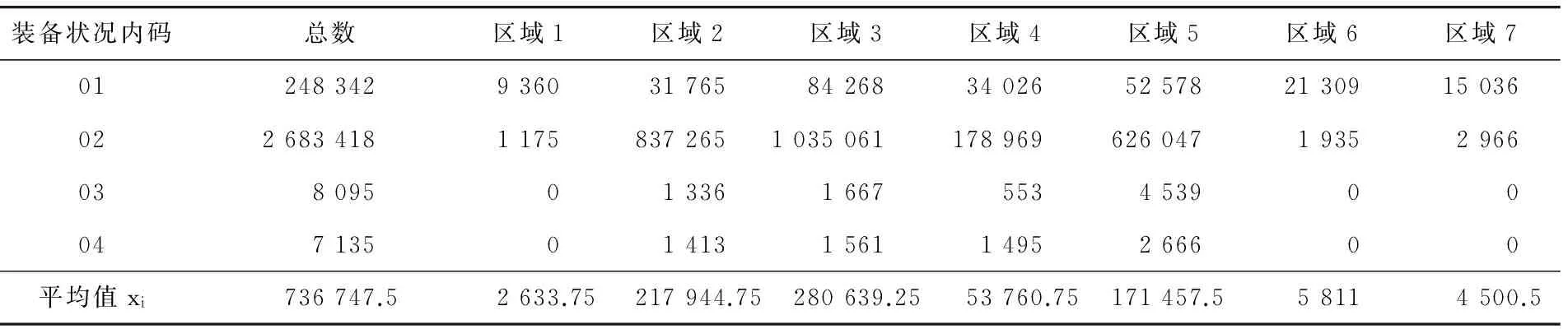
表1　各区域不同状况装备的数量

根据表1中数据，以总数为参考数列x0(t)，以区域1～7对应的x1(t)～x7(t)为比较数列，计算7个区域对于装备总数的关联度。

(1)对各数列作均值化处理。利用表1中装备总数和7个区域的均值去除各原始数列得均值化数列(见表2)。

表2　均值化处理数列

(2)计算各比较数列同参考数列在同一时期的绝对差。

当t = 01时：

Δ区域1(01)=|0.337 1-3.553 9|=3.216 8。

同理，Δ区域2(01)=0.191 3，Δ区域3(01)=0.036 8，Δ区域4(01)=0.295 8，Δ区域5(01)=0.030 4，

Δ区域6(01)=3.329 9，Δ区域7(01)=3.003 9。

再分别计算其余3类状况的装备的各绝对差。全部结果见表3。从中找出最大值和最小值为Δ(max)=3.329 9，Δ(min)=0.000 7。

表3　绝对差计算结果

(3)计算关联系数。取分辨系数ρ=0.2，则计算公式为

当t = 01时：

同理，ξ区域2(01)=0.777 6，ξ区域3(01)=0.948 6，ξ区域4(01)=0.693 1，ξ区域5(01)=0.957 3，ξ区域6(01)=0.168 8，ξ区域7(01)=0.181 7。

用同样方法分别计算其余3类状况的装备的各个关联系数，计算结果见表4。

表4　关联系数计算结果

(4)计算关联度。利用表4，分别求各个数列每个时期的关联系数的平均值即得关联度：

0.986 7)=0.576 5

同理，r区域2=0.884 5，r区域3=0.968 4，r区域4=0.837 1，r区域5=0.978 9，r区域6=0.576 5，r区域7=0.584 0。

(5)排关联序。由关联度数值[6]可看出，r区域5>r区域3>r区域2>r区域4>r区域7>r区域1>r区域6。根据表4作出各区域装备状况联系折线(如图1所示)。

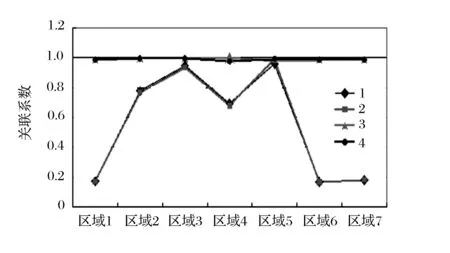
图1　各区域装备状况关联系数折线

由图1可以看出，新品和堪用品的关联系数随区域波动较大，说明新品与堪用品与地域关联性较大。待修品和报废品的关联系数随区域波动较小，说明待修品与报废品与地域关联性较小。

通过排关联序可看出，整体上装备状况在各个区域有差异，区域5对装备状态影响最大，区域6对装备状态影响最小。

3　结　语

本文侧重装备保障信息研究的一个方向，探究了各种因素对装备状态的影响程度，通过模拟验证表明该算法产生的数据结果可靠，运用灰色关联度模型进行分析，从模型中推导出的结论符合客观事实。该方法模型简单易懂，方法灵活性强，具有一定的推广性。

[1]谭学瑞,邓聚龙.灰色关联分析：多因素统计分析新方法[J].华北电力大学学报,2003,30(1):61-64.

[2]刘普寅,吴孟达.模糊理论及其应用[M].长沙:国防科技大学出版社,1998:32-56.

[3]邓聚龙.灰色系统基本方法[M].武汉:华中理工大学出版社,1987:92-114.

[4]申卯兴.分辩系数对灰色关联系数的影响[J].陕西师范大学学报,1999,27(7):81-84.

[5]傅立.灰色理论统计及其应用[M].北京:科学技术出版社,1992:236-243.

[6]袁嘉祖.灰色系统理论及其应用[M].北京:科学技术出版社,1991:57-72.

(编辑：张峰)

Gray Relational Analysis Model of the Equipment Status Affecting Factors

AN Yuchen1, WANG Xingfu1, CHU Kangshuai1,ZHANG Xinwei2

(1. Comprehensive Training Base, Military Transportation University, Tianjin 300161, China; 2. General Courses Department, Military Transportation University, Tianjin 300161, China)

To study the changes of equipment affecting factors,we analyzed the correlation of the factors that affect equipment status. By integrating and analyzing the deployment of troops,the conditions and changes of the equipment in the army, we established a gray relational analysis model, which is verified by simulation to be able to reflect the effects each factor exerts on the equipment.

gray relational analysis; correlation analysis; equipment status

2015- 09-18；

2015-11-17.

安雨晨(1993—)，男，在读本科生.

10.16807/j.cnki.12-1372/e.2016.04.022

E237

A

1674-2192(2016)04- 0091- 04