一道期末统考数学试题的错误分析及思考
2016-09-21浙江省台州市白云学校张安军
☉浙江省台州市白云学校张安军
一道期末统考数学试题的错误分析及思考
☉浙江省台州市白云学校张安军
一、试题呈现
题目:(本题6分)如图1,在△ABC中,D是BC的中点,过D点的直线GF交AC于F,交BG于点G,且AC∥BG,DE⊥GF,交AB于点E,连接EG.
(1)求证:BG=CF;
(2)请你判断BE+CF与EF的大小关系,并证明你的结论.
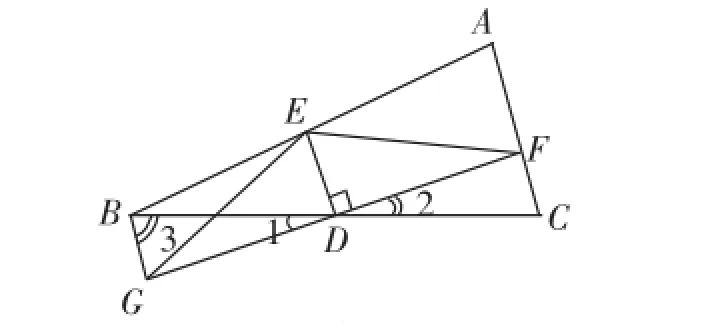
图1
第1小题利用三角形全等,证明两条线段相等.两个三角形全等的确定,从已知条件中可以直接得到对顶角相等,由中点的定义得到线段相等,由两条直线平行得到内错角相等,全等条件基本上都可以直接得到.第2小题在第1小题的基础上,把线段BE、CF、EF通过等量代换集中到△EBG,从而由三角形两边之和大于第三边,就能证得结论.
上述题目是区八年级上期末一道测试题,所用的是人教版《义务教育课程标准实验教科书·数学》八年级上册,该题为试卷的第20题(本卷选择题10题,填空题5题,简答题8题,共23题,100分制),从试题的结构和分布情况来看,命制者把此题放在简答题的第四题,认为此题目不难,是容易得分的题目;同样任课的老师也认为是一道中档难度的试题.然而通过阅卷统计后,教研区的三个学校统计学生得分情况如下表:

人数平均分最高分最低分得6分得0分1032 2.6 6 0 187人179人
学生的错误千姿百态,本文试图对学生的错误答题进行分类整理,呈现部分错误的解答,为一些老师了解学生的学习状态,调整自己的教学,促进因材施教的实施,提供一些依据.
二、错误分类
对于学生作业中的错误,国内外学者已经开展了有益的工作,Newman等人从解题过程角度提出错误的层级,将其分为5个水平:阅读、理解、转换、加工技能、编码.理解错误指的是没有掌握问题中所有信息的意义.操作技能错误指的是与算法有关的错误.编码错误指的是书写错误,如笔误等[1].戴再平先生从解题结果的角度把解题错误分为知识性错误、逻辑性错误、策略性错误、心理性错误[2].本次收集一道几何解答题的解答错误,并且是一次期末考试,它和自然状态下学生的作业重视程度是不一样的.Newman等人是基于学生解文字题得到的研究成果,主要是针对代数内容;戴再平先生过于笼统,缺乏针对性,如逻辑性错误本质上也是知识性错误.鉴于上述原因,把本次收集的错误分成四类,具体如下.
1.不知所云式的错误
阅卷的过程中发现这样一类错误,学生认真作答,写了很多的内容,但所写的内容和答案相差甚远.有的所写内容阅卷老师很难读懂,他们的答题缺乏目标导向,或者仅对已知的条件进行简单的拼凑,推理时缺乏逻辑,不按照数学结构特征和关系去说理,一切都按主观的想法去构建解答.这样一类错误如同两个黄鹂鸣翠柳,不知所云.从中可以发现,这些学生对书本中的概念、定理等基础知识不会理解,或者大部分都不清楚,当然更不清楚它们之间的关系.
[错例1](1)在△GBD和△FCB中,AC∥BG,DG= DF,DE⊥GF.
所以△GBD≌△FCB,所以BG=CF.
(2)由BE+CF=90°,EF=135°,90°<135°,得EF>BE+CF.
对于(1)的解答,证明两个三角形全等时,把已知条件中两线的位置关系平行和垂直作为全等的判定条件;对于(2),在说明线段EF和BE+CF的大小关系时,用角度代替线段的大小,这样的想法让阅卷老师百思不得其解.改完试卷后,在第二学期通过该考生的任课老师了解得知该考生成绩比较差,同时明白为什么得到“BE+ CF”等于90°,该考生的解释是“FC所对∠2=18°,BE所对∠BGE=62°,EF和EG所夹的角∠GEF=135°”.当然如上述考生这样的错误仅仅是个案,但我们经过统计发现存在这样一类错误的学生占9%,他们都很努力地进行解答,还有接近8%的考生是空着不做.按评分标准计分,这两类考生该题的得分都是零分,但两者还是有着区别的,努力地完成解答的学生,他们在整体上对数学还是有所感悟的,比如上述这位学生在证明两条线段相等时,知道用三角形全等的方法;比较线段的大小时,化形为数,用数形结合的思想方法来比较线段的大小,并且这样的学生在学习态度上大都还是端正的,他们愿意配合老师的作业,他们可能存在偏科,他们也努力实现自己的进步,但由于他们接受数学知识比一般的同学要慢得多,更需要数学老师的呵护和关爱.数学课程标准倡导“人人都能获得良好的数学教育,不同的人在数学上得到不同的发展”.其次课堂上设计的问题要有层次性,尽可能照顾到不同层次的学生,让数学基础差的同学也有所收获.
2.大意失荆州式的错误
在阅卷的过程中,发现部分学生读题时不够细心,比如漏看条件,增加了条件,或者错看条件;在审题时,没有挖掘题中的隐含条件,或者想当然当作以前做过的题目,没有发现似曾相识背后问题的不同.在考试时,限时做一份试卷,学生急于把试卷做完,在解答或书写时,有的出现了上下行抄错,有的是抄写时产生错误,如本来想写的答案是甲,结果却写成答案乙等.当然从试卷本身的角度分析,本题条件多、图形复杂、信息量大的特点造成认知负荷,从记忆的贮存、编码到信息的提取过程中容易出现各种错误.这类错误和平常的做题习惯有关,称之为“大意失荆州”式的错误.
[错例2]由D是BC的中点,得GD=FD.
[错例3]由AC∥BG,得∠C=∠BGD.
错例2中“D是BC的中点”本应该是BD=DC,而学生错写成GD=FD.错例3中由“AC∥BG”可得到“∠C=∠3”,但学生却错写成“∠C=∠BGD”.除此之外,还有比如三角形全等要按照对应点的顺序来写,学生却错写成“△GBD≌△DFC”,犯这样一类错误的学生千姿百态,数学优秀生或困难生都有着不同程度的体现.究其原因,一部分是由于平常做作业时,没有养成良好的书写习惯,做作业时未曾集中注意力,如边看电视边做作业,长期以往形成不良的习惯,还有客观上的原因,本题的题意较长,语言叙述烦琐,信息量多而散乱,记忆的贮存容易遗失或增加,这样考生提取信息时,出错率相对就高.对于上述这样的错误,如何有效地避免呢?学生养成良好的书写习惯除了专心致志做作业外,还要减少作业,老师不要注重作业量完成的多少,要注重作业的品质,布置作业前,老师自己先做题目,精选题目,避免重复;其次,为了体现考试的信度和效度,在题目语言叙述上做到精练,条理清楚.如把原题改写为下面的叙述.
如图1,过△ABC边BC的中点D作直线交AC于F点,并同时与过B点且与AC平行的线交于点G.
(1)求证:BG=CF;
(2)E为AB上的动点,连接EG、EF,当DE⊥GF时,判断BE+CF与EF的大小关系,并证明你的结论.
改编后的题目与原题相比,题干变得简洁、明了,信息的干扰少,易于第1小题的解答;同时第1小题的顺利解决,为第2小题的解答带来了便利.
3.扑朔迷离式的错误
在阅卷过程中,有这样一类错误,学生对基本概念、性质的理解比较模糊,混淆定理应用的条件,数学语言表述不准,理由不够充分,逻辑推理混乱,缺乏因果.这类错误是由于对数学概念和定理等缺乏理解,分不清相近概念之间的关系,把这样一类错误称之为雌雄难辨、扑朔迷离式的错误.
[错例4](1)由D是BC的中点,得BD=DC,GD=DF.
在△GBD和△FCB中,BD=DC,∠1=∠2,GD=DF.
则△GBD≌△FCB,则BG=CF.
(2)在Rt△EGD和Rt△EDF中,ED=ED,GD=DF,则△EGD≌△EDF(HL),则EG=EF.
又BG=CF,在△GBE中,BG+BE>GE,则CF+BE>EF.
错例4中的第1小题,把“中点的定义”和线段“互相平分”两个概念混淆,同时无法准确地找出条件和结论之间的关系,无法排除无关条件和信息、挖掘隐含条件,如没有察觉到两直线“AC∥BG”这一条件;第2小题在证明两个直角三角形全等时,把两条边相等都当作直角三角形的“HL定理”,混淆了“HL定理”和一般三角形全等的区别,对具体问题不具体分析,机械地运用结论,出现张冠李戴的现象.
如何化解学生知识性等错误呢?首先要让学生学会审题,分解题意中的关系和结构,对图形语言、自然语言、符号语言之间的关系进行转换,挖掘隐含条件的信息,从而建立结论和条件之间的通道;其次,在教学中要重视数学中的基本概念、定理、公式等教学,注重结果的同时,更应关注学生对概念和定理等形成过程的教学,只有这样,学生才能清楚知识的来龙去脉,清楚知识间的联系和区别,注重解题后的归纳总结和反思,注重数学思想方法的提升,这样才能综合运用相关的知识.
4.南辕北辙式的错误
在阅卷过程中,部分学生对第1小题解答思路清晰,条理清楚,然而在第2小题的解答过程中,出现了方向性的错误.第2小题是开放型的问题,由于猜想出现错误,考生为了证明自己的结论,达到自己的目的,缺乏正确的心理势态,没有从反向思考,对自己的猜想进行质疑,为了证明自己的结论,有的悄悄增加了条件,错误接连不断,也不遵从逻辑规则,任意得到想得到的结论,这样的错误称之为南辕北辙式的错误.
[错例5]猜想的结论:BE+CF=EF.
由△GBD≌△FCB,得EF=EG.
由DE⊥GF,得△GBD是直角三角形.
则∠EGB=60°.
则△GBO是等边三角形.
则BG=OG.
由CF=BG,得CF=OG,则BE+CF=EF.
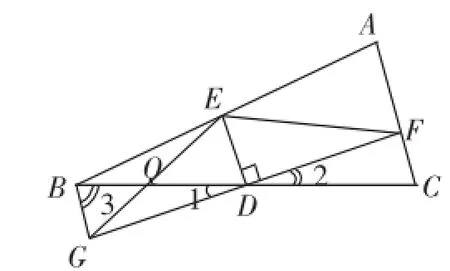
图2
其次,课堂中应让学生亲身经历从“大胆的猜想”到“小心的求证”这样一个思维的否定之否定的过程.这是因为数学中的合情推理和演绎推理是从已有的事实或经验出发,凭借经验或直角,通过归纳或类比推断某些结果.由于合情推理的结论不一定正确,因此有必要对归纳得到的结论进行验证.从猜想、假设、质疑再到新的猜想、假设、质疑是循环往复的,如上述问题中“BE+CF与EF的大小关系”的猜想,有同学得到这样的猜想:“BE+CF=EF”或“BE+CF<EF”,通过实际测量或者从已有的事实知识出发进行验证,当发现这一结论与测量的结果不符合实际,或者不能从已有事实推出时,就转向质疑并否定,于是产生新的猜想和验证.因此在教学过程中,要让学生经历从假设猜想到质疑否定这样一个批判性思维的形成过程,也是在平常教学中“思考”的沉淀,是在数学学习活动过程中逐步积累的.
除了上述错误,还发现了一些问题,如学生书写字迹了草,还有很多学生解决此题思维不简洁,烦琐复杂,缺乏思维的灵活性,缺乏对新知识的迁移.例如上述问题中在证明“EF<BE+CF”时,为了证明“GE=EF”,没有用已知条件DE⊥GF和已证得的结论GD=DF,当然利用这两个结论可得到ED是线段GD的垂直平分线,从而得出“GE=EF”.然而学生舍近求远利用“△GED≌△FED”去证明“GE=EF”,“线段垂直平分线”的性质是图形与几何中的核心知识,利用这个性质可直接证明线段相等,它们是全等三角形特殊的推广,阅卷的过程中大部分学生不自觉运用三角形全等去证明线段相等,在一定程度上反映出教师没有注重解题过程中举一反三、触类旁通,没有重视解题后归纳、反思和思维的优化等.
三、对错误的思考
一花一世界,一点雨露能映照出大自然的光辉,同样学生的错误也可折射教与学存在的问题,学生的很多错误是有规律的而不是偶然的,从学习者身上观察到的一系列错误表明,错误不是教给的,而是学习者构造了自己特有的概念和程式造成的.学生在解题中出错是学生解题的必然行为,教师对错例的剖析是解题教学的一部分,因此教师要善待学生的错误,既要适当暴露学生的错误给出补救和纠正,又要在教学上进行反省;既要消除错误的负面影响,又要让错误散发出正能量.同时对错误的修正也不能光靠教师的讲解和不断的强化,其更好的途径是发挥学生的主体作用,进行反思质疑,从而提高错误修正的效果.
1.黄兴丰,等.初中生在几何解题中所出现错误的调查研究[J].数学教育学报,2003(8).
2.戴再平.数学习题理论[M].上海:上海教育出版社,1996.
3.应建军.初中数学“五步归一”错例修正法的实践与探索——以一道作业本习题为例[J].中学数学(下),2015(6).Z
