“听课检测”:解题教学的必要跟进
2016-09-21江苏省江阴市青阳第二中学于永红
☉江苏省江阴市青阳第二中学于永红
“听课检测”:解题教学的必要跟进
☉江苏省江阴市青阳第二中学于永红
数学学习离不开解题,数学教学自然也离不开解题教学,然而不少解题教学常常是教师讲好了数学题,然而安排学生自主订正时,有些习惯不好、自主性不高的学生常常满足于课上似乎听懂,简单修改答案式的订正应付一下.在目前大班额的班级教学中,学生整体上掌握、巩固到什么程度,往往缺少必要的反馈,这也许是导致很多解题教学效率偏低的原因.笔者近年来尝试开展“听课检测”活动,即在解题教学之后,对相关习题进行恰当的变式改编后安排跟进检测,实践一段时间之后,取得了一定的效果.本文呈现几个题例,并给出解读与反思,供研讨.
一、题例呈现与解读说明
题1:如图1,在▱ABCD中,AE⊥BC于E,AF⊥CD于F,且∠EAF=60°,BE=2,CF=1.求AF的长.
解题教学记录:这是相关教辅资料上的一道习题,讲评时重点是引导学生把目光聚焦在△ADF、△ABE中,突破了AB、DF的长之后,就获得了重要进展.基于讲评重点,我们改编了如下的听课检测题,检查学生的听课效果.
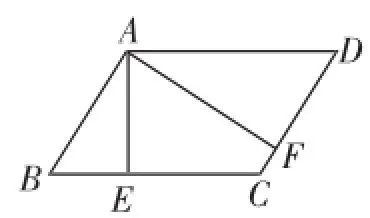
图1
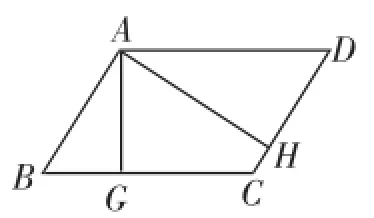
图2
听课检测题1:如图2,在▱ABCD中,AG⊥BC于G,AH⊥CD于H,且∠GAH=60°,BG=2,CH=1.
(1)求∠B的度数;
(2)求DH的长;
(3)求▱ABCD的面积.
改编说明:保持了问题题干的不变,只是简单变式了垂足的字母,增设了第一问,让一些学困生也能上手,吸引更多学生参与,又拓展出了第三问,避免优秀学生只是停留在原题上“空转”一次.
题2:如图3,在▱ABCD中,M、N分别是AD、BC的中点,BC=2CD.求证:四边形MNCD是平行四边形.
解题教学记录:如果只是满足于证明平行四边形,则入宝山而空返.笔者曾将该题做出一些即兴变式,通过添加一些条件,比如∠C等于60度,增加解题层次,引导学生继续深入思考可能导出的一些结论,以下就是讲评之后设计的听课检测.
听课检测题2:如图3,在▱ABCD中,M、N分别是AD、BC的中点,BC=2CD.
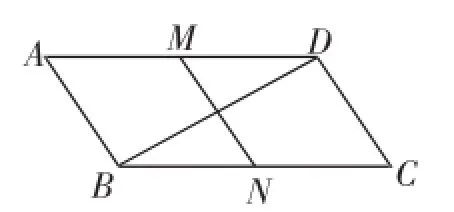
图3
(1)求证:四边形MNCD是平行四边形.
(2)当∠C=60°、MN=2cm时,
①求BD的长;
②连接AN交BD于G,求GN的长.
改编说明:保留了第一问,但通过添加强化条件“∠C=60°,MN=2cm”增设出两个问题,把问题引向深处,不但训练了平行四边形的证明,而且还把学生的思考引向特殊直角三角形(含30°)与特殊四边形之间的关系.
题3:如图4,△ACB和△ECD都是等腰直角三角形,△ACB的顶点A在△ECD的斜边DE上.求证:AE2+AD2= AB2.
解题教学记录:这道习题来源于人教版教材,条件与待证结论之间的距离较远,所以不少学生感觉到困难,笔者曾设计如下追问启发思路,比如连接BD,能证出哪两个三角形全等?△ABD有何特殊?边AD、BD、AB之间有怎样的数量关系?等等.通过上述追问,使得学生获得思路的贯通.于是,讲评之后,我们设计了如下的听课检测题.
听课检测题3:如图4,△ACB和△ECD都是等腰直角三角形,△ACB的顶点A在△ECD的斜边DE上,连接BD.
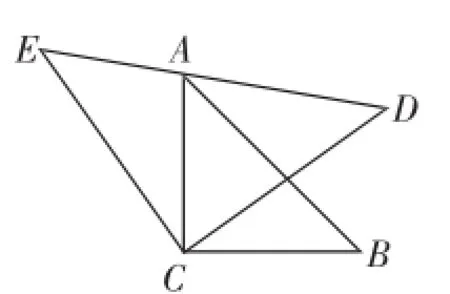
图4
(1)求证△ACE≌△BCD;
(2)求∠ADB的度数;
(3)若BD=2,AD=3,直接写出AB的长;
(4)求证:AE2+AD2=2AC2;
(5)当∠BCD=30°、BC=2时,求△ACE的面积;
挑战:(6)作CH⊥AD,垂足为H,若CD、CH与AB分别交于M、N,AN=2,BM=2,直接写出△ACB的面积.
改编说明:前面四问是原题的再检测,前三问是服务于第四问的;为了防止优生“空转”,增设出第五、六问,比如第五问,要求学生有较强的抗干扰能力,分离聚焦到△ACE中,作出CE边上的高,实现思路突破;而第六问隐含了一个结构,即图5中,发现∠DCH=45°后,应该能洞察出AN2+BM2=MN2.这样才能快速获得边AB的长,为最终求得△ABC的面积打开思路.
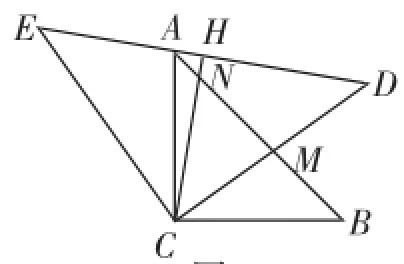
图5
题4:如图6,分别以Rt△ABC的直角边AC及斜边AB为边向外作等边△ACD、等边△ABE.已知∠BAC=30°,EF⊥AB,垂足为F,连接DF.求证:四边形ADFE是平行四边形.
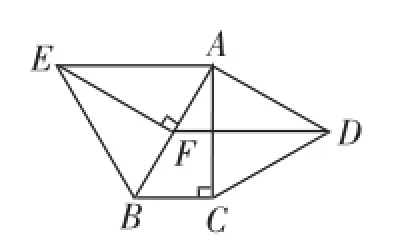
图6
解题教学记录:这道习题学生初次练习时的一个易错点是“想当然”地认为∠AFD=60°,缺少必要的推证,从而很快利用两组对边分别平行证出结论,造成“会而不对、对而不全”的错漏解法.讲评时重点解说了全等沟通边相等、利用一组对边平行且相等的思路证明平行四边形,并开发了如下的听课检测题.
听课检测题4:如图6,分别以Rt△ABC的直角边AC及斜边AB为边向外作等边△ACD、等边△ABE.已知∠BAC=30°,EF⊥AB,垂足为F,连接DF.
(1)求证:△AEF≌△BAC;
(2)求证:DF=AB;
(3)求证:四边形ADFE是平行四边形;
(4)若BC=2cm,求四边形ADFE的面积;
(5)设AC、DF相交于G,连接BG,若AD=4cm,求BG的长;
挑战:(6)在(5)的条件下,连接EG,求四边形AEGD的面积.
改编说明:为了帮助更多的学困生理解该题证明平行四边形的路径,增设了第一、二问;为了给优秀学生提供更高要求,引发深入思考,增设了第四、五问,达到了较好的检测评价的效果.
二、进一步的思考
1.听课检测帮助学生从“听懂”走向“会做”
在一线教学的老师都有同感,很多同学听课时总以为自己已经听懂,然而让他们再独立解答类似问题时,却往往还不到位,这说明所谓“听懂”与“会做”之间还有一定的距离,这个距离可以通过跟进设计同类的“听课检测”来促进学生真正学会.有必要时,还可以在听课检测之后再次进行讲解,学生之间互评、教师对话追问其他同学的理解和不同思路,实现解题教学的高效,也是追求“做一题,会一类,通一片”的教学效果.
2.听课检测需要教师修炼命题基本功
从上面提供的几个题例来看,听课检测需要教师认真研究试题,精心设计较难问题的台阶、铺垫,既追求不同小问之间的由浅及深、从易到难的排列,又使得并列式问题之间互相关联、前后呼应、思路启发,这就需要教师有扎实的命题基本功.事实上,这方面的命题基本功不仅在习题教学上大有益处,在教学设计中也是十分必要的,比如数学课上一般都需要选用例题,而且往往也需要对例、习题展开变式,如何变式,变式角度有哪些,呈现方式如何等,都是需要教师精心设计的.
三、写在最后
有人把“学习方式”比喻成“消化能力”,认为如何练习和学习机制存在问题,学生就会“消化不良”,长此以往,就会“积食”,丧失胃口,自然也就不堪重负.有识之士也指出“减轻过重的课业负担,重在教学设计、教学研究”,我们深有同感.如果能把精心选择出来的典型习题认真讲评,并做好跟进检测,那么是不是就可以有效避免“同一类问题反复出现在17张试卷上”这种“题海现象”呢?
1.余慧娟,施久铭.减负,教育到底能做什么[J].人民教育,2009(5).
2.中华人民共和国教育部制定.义务教育数学课程标准(2011年版)[M].北京:北京师范大学出版社,2012.
3.郑毓信.“开放的数学教学”新探[J].中学数学月刊,2007(7).
4.章建跃.构建逻辑连贯的学习过程使学生学会思考[J].数学通报,2013,56(6).
5.刘东升.经历问题生成,深刻理解教材——人教八上“每日一题”的命题实践与思考[J].中学数学(下),2014(4).Z
