利用几何图形的轴对称性解题
2016-09-21江苏省泰州市第二中学附属初中曹文喜
☉江苏省泰州市第二中学附属初中曹文喜
利用几何图形的轴对称性解题
☉江苏省泰州市第二中学附属初中曹文喜
两个图形成轴对称是指把其中一个图形沿着某一条直线翻折,它能够与另一个图形重合.根据这个定义得到成轴对称图形的基本性质:任一对对应点的连线段都被对称轴垂直平分.解题时根据命题的条件及图形的特征,运用图形的轴对称性来探索解题思路,可以迅速找到许多问题的解题途径.初中几何中,等腰三角形、正方形和菱形等是典型的轴对称图形,把它们位于对称轴两旁的部分看成两个图形,那么这两部分就成轴对称.现举例说明如下:
一、利用等腰三角形的轴对称性解题
等腰三角形是轴对称图形,它的底边上的高(或底边上的中线或顶角的平分线)所在的直线就是它的对称轴.如果把它看成两个图形,那么这两个图形就是成轴对称图形.
例1证明等腰三角形的两底角相等.
分析:此题的常规证法是通过作等腰三角形底边上的高而得到两个全等的三角形,从而由对应角相等来证明命题成立.若我们能发现△ABC与△ACB的对称性就能够更简单地证明.
证明:如图1所示,在△ABC与△ACB,因为∠A=∠A,AB=AC,AC= AB.所以△ABC≌△ACB.因此∠B=∠C.
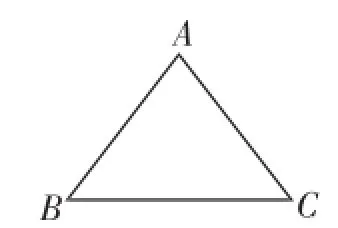
图1
二、利用正方形的轴对称性解题
正方形是一种典型的轴对称图形,它有四条对称轴,其中它的对角线所在的直线也是它的对称轴.通过观察它的对角线,可以发现对角线两旁的部分呈轴对称,其对应的线段相等,对应的角相等,这样就能进行相等线段之间的转化和相等角之间的转化,从而发现解题的思路.
例2如图2,在正方形ABCD中,P为对角线AC上任意一点,PE⊥AB,PF⊥BC,垂足分别为E、F.求证:PD=EF.
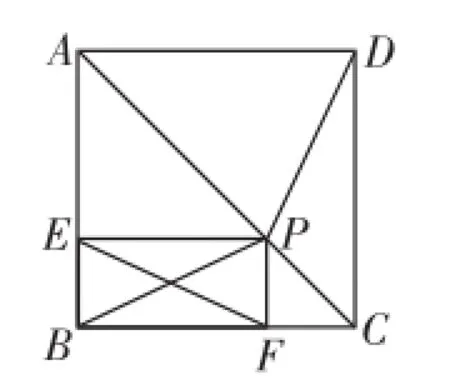
图2
分析:初略一看,EF只是两个直角三角形的斜边,而PD所在的两个三角形不一定是直角三角形,似乎无法证明PD和EF相等,但是换个角度,考虑到对角线所在的直线也是正方形的对称轴,连接PB,根据对称性立即发现PD=PB(当然规范解题时可以通过证明两个三角形全等得到);这样就转化为求证EF和PB相等的问题,而EF和PB是矩形的两条对角线,显然相等.
证明:因为四边形ABCD是正方形,所以AB=BC= CD=DA,∠ABC=∠CDA=90°,所以∠BAC=∠DAC=45°.在△BAP和△DAP中,所以△BAP≌△DAP(SAS),所以PB=PD.
又因为PE⊥AB,PF⊥BC,所以∠PEB=∠PFB=∠ABC=90°.
所以四边形EBFP为矩形,所以EF=BP,所以PD=EF
例3如图3,在正方形ABCD中,F为CD上的一动点,EM垂直平分BF交AC于点E,垂足为M,求∠EBF的度数.
同时,含沙量沿垂线分布逐渐减小,其中大潮情况下,底层含沙量为表层含沙量的2.75倍,小潮情况下为1.22倍。表明大潮期间因流速显著大于小潮,海床与水体间的泥沙交换活跃,近底层含沙量相对较高,水体泥沙均表现出有较多当地掀扬泥沙参与的特点。
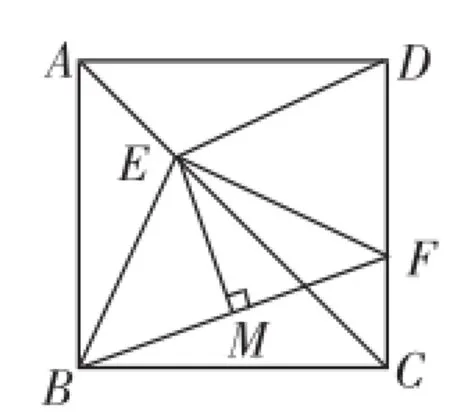
图3
分析:根据正方形的对角线所在的直线是它的一条对称轴,通过观察,立即就会发现线段EB=ED,∠EBC=∠EDC.又因为EM垂直平分BF,得EB=EF,所以ED=EF,这样∠EFD=∠EDF,所以∠EFD=∠EBC,这样根据四边形的内角和等于360°,就能得到∠BEF=∠BCF=90°,于是得出△EBF是等腰直角三角形,所以就可求出∠EBF=45°.
解:因为四边形ABCD是正方形,所以AB=BC=CD= DA,∠ABC=∠BCD=∠CDA=90°,∠BAC=∠DAC=45°.在
因为∠EFD+∠EFC=180°,所以∠EBC+∠EFC= 180°.
又在四边形EBCF中,∠EBC+∠BCF+∠EFC+∠FEB=360°,所以∠BCF+∠FEB=180°.
又∠BCD=90°,所以∠BEF=90°,所以△EBF为等腰直角三角形,所以∠EBF=45°.
三、利用菱形的轴对称性解题
菱形的对角线平分一组对角,它的对角线所在的直线就是它的一条对称轴.因此能够找到菱形的一边上的点关于它的对角线的另一对称点,从而就可以找到解题的思路.
例4如图4,在菱形ABCD中,P为对角线BD上的一个动点.
(1)若G、Q分别为边BC、CD的中点,则点P在何处时使PG+PQ最小;
(2)若G、Q分别为边BC、CD上的动点,则PG+PQ的最小值是什么?
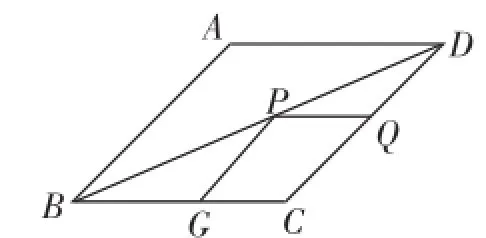
图4

图5
分析:菱形的对角线平分一组对角,因此菱形的对角线所在的直线是它的一条对称轴.Q是CD上的一点,所以Q点关于直线的对称点在边AD上,这样就将此题转化为三点共线的问题.
解:(1)如图5,取AD的中点Q′,连接GQ′与BD相交于点P,这时PG+PQ最小.
因为四边形ABCD是菱形,所以AB=BC=CD=DA.
又Q、Q′分别为边CD、DA的中点,所以DQ=DQ′.
根据两点之间线段最短,所以连接GQ′与BD相交于点P,这时PG+PQ最小.
(2)如图6,由上题可知菱形ABCD是关于对角线BD成轴对称的,所以动点Q关于BD的对称点Q′应该在AD上,且PQ=PQ′.

图6
当三点Q′、P、G共线且Q′P最短时,满足结论.因为AD∥BC,根据两平行线间垂线段最短且处处相等,所以PD+PQ的最小值就是菱形ABCD的高.
总之,我们解题时,要注意观察图形、善于利用几何图形的轴对称性,找出对应角和对应线段,再根据题目所给的已知条件,进行分析、探索,这样就能够快捷地找到解题的途径.H
