如何用尺规将一个角三等分
2016-09-21江苏省盐城市尚庄初级中学刘志才唐明干江苏省盐城市葛武初级中学王云峰
☉江苏省盐城市尚庄初级中学刘志才唐明干☉江苏省盐城市葛武初级中学王云峰
如何用尺规将一个角三等分
☉江苏省盐城市尚庄初级中学刘志才唐明干
☉江苏省盐城市葛武初级中学王云峰
一、三分角的雏形
如图1,已知一定角∠MON,AL∥OM,如何将角∠MON三等分呢?设两平行线OM、AL间的距离为m,则在AL上必存在一点B,在ON上必存在一点C,且B、C两点均是唯一的,使得OB=OC、BC=2m,作BE⊥OM于点E,作OD⊥BC于点D,可得BE=BD=CD=m,易得Rt△OCD≌Rt△OBD≌Rt△OBE,从而得到∠1=∠2=∠3=∠MON.

图1
二、初步探索与研究
为了能得到上面所说的△OBC,我们从图2入手,加以研究.
如图2,以点O为圆心,大于OA之长为半径依次画弧,分别得到等腰三角形OFG、等腰三角形OHI、等腰三角形OJK、…,在这若干个等腰三角形中,要找到底边长为2m的等腰三角形OBC,几乎不可能的.
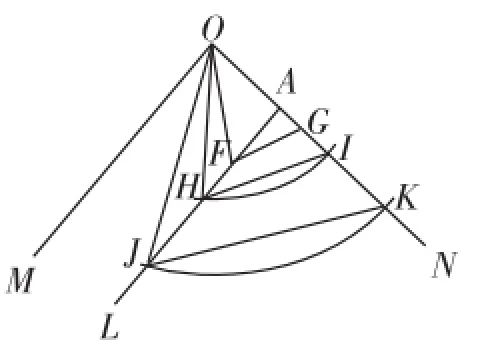
图2
三、图形重组找规律
如何将等腰三角形OBC找出来呢?我们进行了以下的尝试:将所有等腰三角形重新组合.方法是:以定点O为旋转中心,旋转△OFG、△OHI、△OJK、…,使它们都以ON为对称轴,分别得到等腰三角形OF′G′、等腰三角形OH′I′、等腰三角形OJ′K(′、…(,如图3(要求:所作两平行线间的距离越大越好,、、(对应的弦长FG、HI、JK均接近并大于2m,后面的证明、作图都是在满足这一要求的范围内进行研究和操作的,这样做的目的将在后面作出说明).
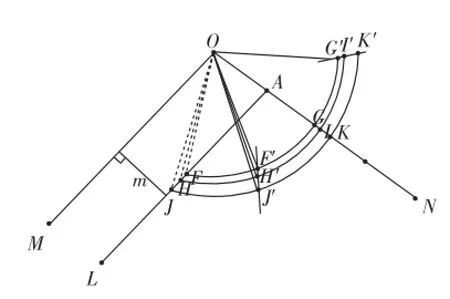
图3
在这个重新组合的图形中,位于对称轴ON左边的所有等腰三角形底边上的端点F′、H′、J′、…是否在一条直线上呢?如果是,那么根据轴对称图形的性质得,位于对称轴ON右边的所有等腰三角形底边上的端点G′、I′、K′、…也在一条直线上.这样,顺利得到△OBC旋转后所得到的图形△OB′C′底边上的端点B′、C′亦分别在这两条直线上.这就是我们所期望得到的一个有规律可循的图形.
如图4,在这个有规律可循的图形中,我们就能够轻而易举地找出我们想要的△OBC旋转后的图形△OB′C′,然后,依据所作图形的唯一性和变换的可逆性,将△OB′C′回归到它原来的位置上,便得到图1中的△OBC,从而解决问题.
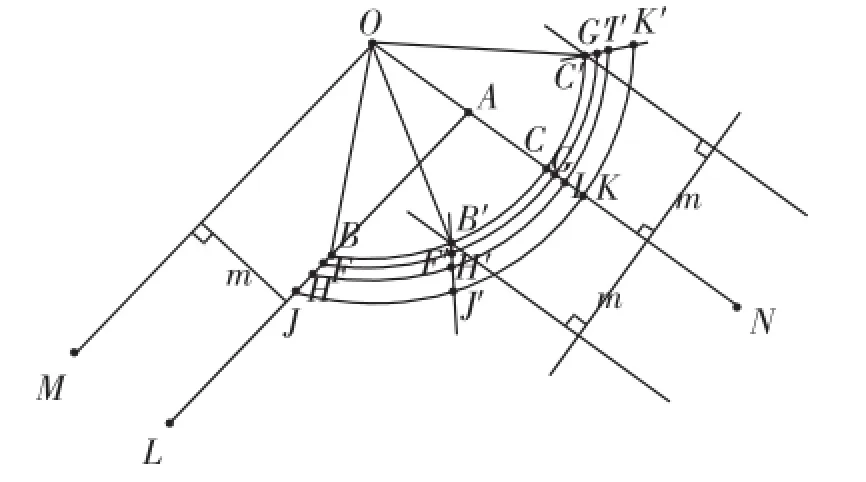
图4
四、相关证明得结论
如何证明F′、H′、J′、…在同一条直线上,G′、I′、K′、…在另一条直线上呢?下面,我们从图5入手加以研究.
1.相关理论证明
如图5,因为等腰三角形OH′I′、等腰三角形OJ′K′是分别由等腰三角形OHI、等腰三角形OJK旋转后得到的,所以;根据轴对称图形的性质可知,所以.所以H′、J′分别是H(I、JK(的中点,过点H′、J′作直线H′J′,在直线H′J′上取一点S′,以O为圆心,OS′长为半径画弧交AL于点S,交ON于点P,则S′必为P(S的中点(要求:所取S′点越接近于J′点越好).
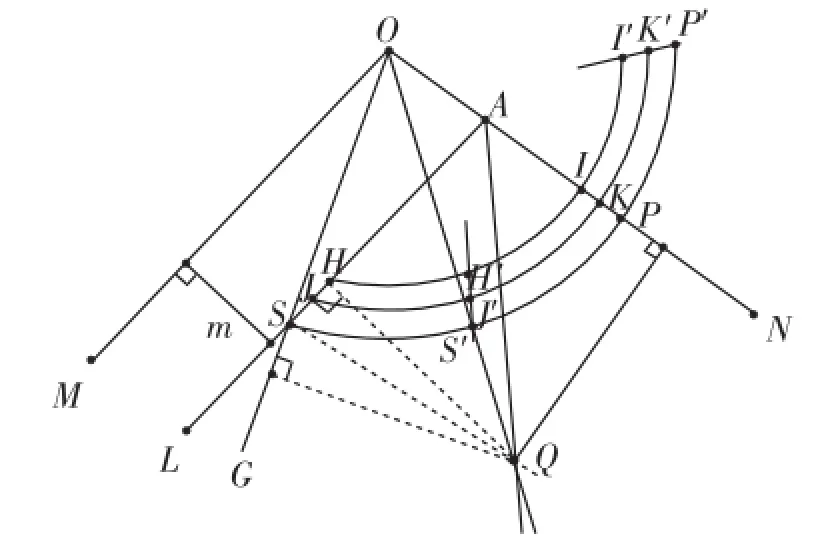
图5
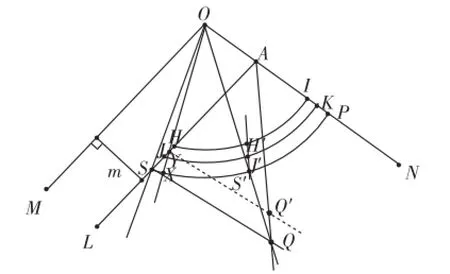
图6
②设S′为?的中点(X′在?上点S的左侧).如图7,连接OX′交AL于点Y′,这时OQ为△Y′OA的内角平分线,AQ为△Y′OA的外角平分线,两角平分线相交于点Q,而Y′Q″为△Y′OA的第三个外角∠AY′Z的角平分线,交AQ于点Q″,显然亦与三角形的一个内角平分线和它的一个外角平分线的交点必在第三个外角的平分线上相矛盾,所以S′不是′的中点,所以S′必为的中点,如图5,由此可推得H′、J′、S′、…在同一条直线上,即旋转后,位于对称轴ON左侧的等腰三角形的端点H′、J′、S′、…在同一条直线上.由轴对称图形的性质可知,位于对称轴ON右侧的等腰三角形的端点I′、K′、P′、…在同一条直线上.
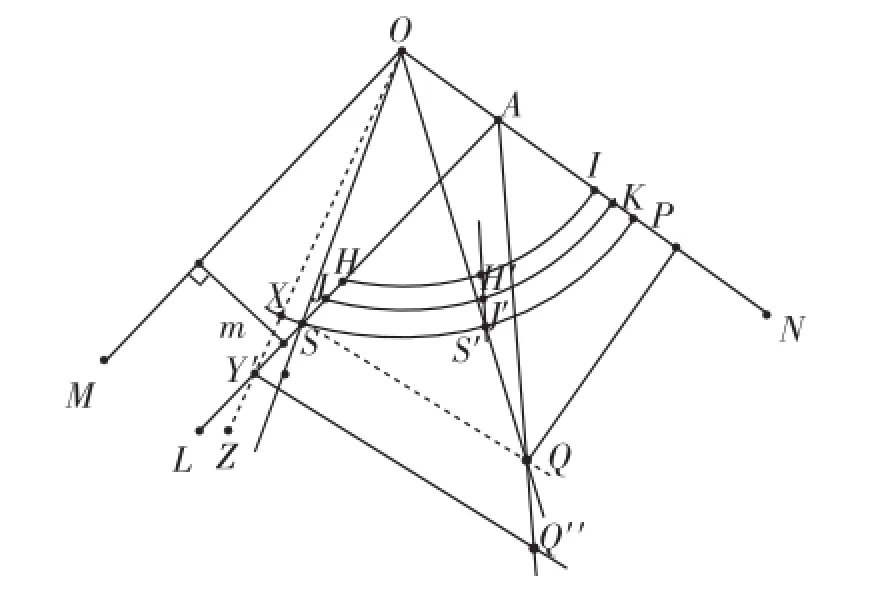
图7
2.相关实验证明
为了验证H′、J′、S′、…是否集中在同一条直线上,我们用大纸、细笔,做了如下的实验.即尽量拉大两平行线间的距离,并画出若干段弦长均接近于并大于2m的弧,再找出所有弧的中点,最后进行描点、连线,结果我们发现所有弧的中点的确都集中在同一条直线上,如图8.

图8
五、按图索骥
既然旋转后的等腰三角形底边上的端点都分别集中在两条直线上,那么,△OB′C′的两个顶点B′、C′亦在这两条直线上,我们就可以在这个有规律可循的图形中,找出△OB′C′,具体找法见图4(作法略).
六、图形回归解决问题
我们所求得的图形△OB′C′是由△OBC旋轴后所得到的图形,且旋转后的图形是唯一的,B、C两点的对应点在直线上唯有B′、C′与之对应,由变换过程的可逆性,我们再将△OB′C′回归到它原来的位置上,便得到图1中的等腰三角形OBC,从而解决问题(作法略,见图4).
七、唯物辩证法则在三分角中的应用
我们在图9中,不难看出,所有弧的中点的集合,是一支曲线.这是我们对于图9作了微观上的处理结果.即将图形扩大若干倍,给我们的直觉就是将两平行线之间的距离扩大了若干倍.既然是曲线,但为什么说所有弧的中点在一条直线上呢?这是因为,我们又对于图9作了宏观上的处理,将图9缩小若干倍的结果,给我们的直觉就是将两平行线之间的距离缩小若干倍.如图10,为图9缩小若干倍的图形.从图10中不难看出,所有弧的中点的确在一条直线上.这条直线,几乎为∠LAN的平分线.但是,问题来了,我们无法在这个宏观的图形(图10)中进行三分角作图.因此,我们的方法是:作图时将图形进行微观上的处理,即将图形扩大若干倍(也就是尽量扩大两平行线之间的距离),目的是将局部曲线直线化,同时也方便我们的操作,有一目了然的作图痕迹.在取弧的中点连线时,我们又进行了宏观上的处理,这就要求我们对所有所取弧的对应的弦长尽量接近并大于2m.这样做的目的,就是对局部的曲线作宏观上的处理,使局部曲线直线化.我们的理论证明和实验证明正是应用了上面的方法来进行处理和研究的.那么,在同一图形中,既进行宏观处理,又进行微观处理,是不是互相矛盾呢?其实不然,这正是在同一事物中矛盾的对立与统一法则的应用.因此,在一定的条件下,矛盾的双方,可以互相转化.我们以上的证明和下面的作图实例,正是运用了这一法则.我们从图9和图10的对比中,可以明显地看出,图10中的直线,正是由于我们将图9中的曲线宏观后直线化的结果.
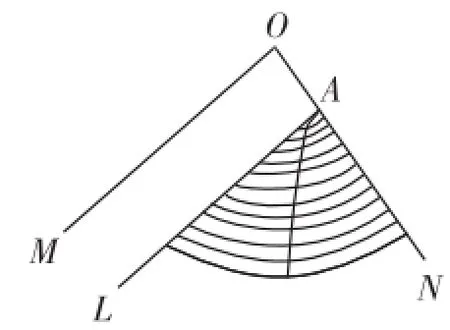
图9
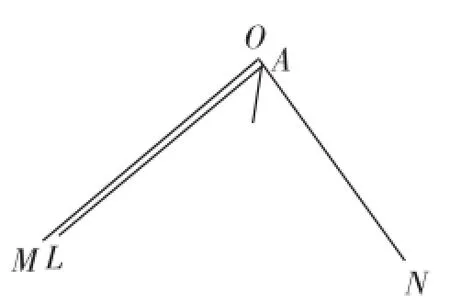
图10
上面我们还提到将曲线宏观后呈直线的实例,如图9、10,我们从图9和图10的对比中还发现较长部分的曲线宏观后成为较短的线段,所以宏观给我们的另一个直觉就是点与点之间的距离接近了、缩短了,就像将弹簧压缩变短了一样.我们为什么要求所取弧的弦长均接近于并大于2m,也就是为了压缩点与点之间的距离,以达到宏观上处理的要求,从而将局部曲线直线化.其实,当我们截取曲线中的极小部分时,这个极小部分的本身就是一条直线,这是一个不容置疑的事实.因为这个极小部分就是我们上面提到的留在纸面上的一条直线.微观曲变直,具有将局部范围内的曲线拉伸后变长、变直之涵义;宏观曲变直,具有将局部范围内的曲线压缩后变短、变直之涵义.这个世界上没有真正意义上的直线,只不过是从局部看来变得曲度更小,更加扁平、平滑而已.这样局部范围内的曲线先经过微观上的处理,又再次经过宏观上的处理后,最终将局部范围的曲线直线化.
在研究中,我们还发现,当∠MON小于45°时,所作三分角可精确到十万之一;当∠MON大于45°且小于180°时,所作三分角可精确到万分之一.为什么不能完全三分角呢?其道理很简单,因为我们上面说过,这个世界上没有真正意义上的直线,只不过是从局部看来曲度更小而已,这和二分角也有误差的道理是一样的.三分角的作图方法同样适合二分角,当两平行线间的距离为0时,这时所有弧的中点的集合为∠MON的平分线,所以二分角的精确度会更高.
八、三分角的作图实例
如图11,已知∠MON,试将其三等分.
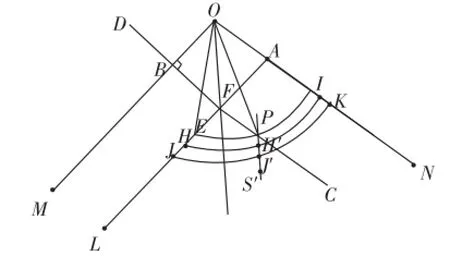
图11
作法:(1)在ON上任取一点A,作AL∥OM(两平行线间的距离越大越好,即实施微观上的处理);
(2)作∠MON的角平分线交AL于点F;
(3)过点F作FB⊥OM于点B,设FB=m,在射线FB上截取BD=FB=m;
(4)以O为圆心,依次画?和?,使得线段HI和JK的长均接近并大于2m(越接近并大于2m三分角的精确度越高,即实施宏观上的处理),两弧分别交AL于点H、J,交ON于点I、K;
(6)过点F作FC∥ON,FC交直线H′J′于点P;
(7)以O为圆心,OP长为半径画弧,交AL于点E,连接OE、OP,则OE、OP三等分∠MON.H
