值得关注的安徽中考数学卷“第14题现象”
2016-09-21安徽省蚌埠市新城实验学校高厚良
☉安徽省蚌埠市新城实验学校高厚良
值得关注的安徽中考数学卷“第14题现象”
☉安徽省蚌埠市新城实验学校高厚良
安徽省中考数学试卷同时具有“初中毕业学业水平考试”和“高中招生考试”的功能,为体现试卷的区分选拔功能,安徽卷采用多点压轴的形式.而作为填空题最后一题的第14题,由于其独特的考查形式(多选题型填空题)、新颖的立意、可信度高、客观性强的特点,被称为安徽中考试卷的“第14题现象”,往往倍受关注.笔者拟选取近五年安徽中考数学试卷的第14题进行赏析,以期发现某些“共性”,服务于2016年中考.
一、近五年安徽中考卷第14题赏析
例1(2015年)已知实数a、b、c满足:a+b=ab=c,有下列结论:
解析:由a+b=ab=c和c≠0,可知a+b=ab≠0,根据等式性质两边同除以ab,可得,故①正确.
对于④,可分三种情况讨论:a=b≠c、b=c≠a、a=c≠b,分别把每一种情况代入题干等式中确定出a、b、c的值,看是否与每一种情况一致,最终可确定a=2,b=2,c= 4,a+b+c=8,故④正确.
赏析:本题作为填空题的压轴题,是安徽卷的特色题,题目以学生熟悉的连等式为背景,综合考查分式的运算、等式的性质、一元一次方程的解法、一元二次方程的解法、解二元一次方程组等核心知识点,同时考查学生代数恒等变形的能力和分类讨论思想、转化思想、方程思想等.四个结论的设置从四个思维角度展开,彼此之间又有着一定的关联,有效考查了学生的分析转化能力和深入探究能力,对学生的思维能力要求较高.
例2(2014年)如图1,在▱ABCD中,AD=2AB,F是AD的中点,作CE⊥AB,垂足E在线段AB上,连接EF、CF,则下列结论中一定成立的是_______.(把所有正确结论的序号都填在横线上)
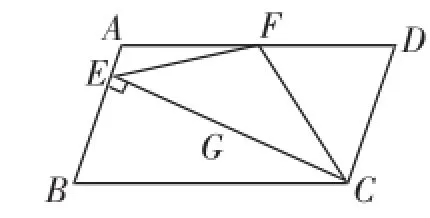
图1
解析:由点F是AD的中点,AD=2AB,得CD=DF.所以∠DFC=∠DCF.因AD∥BC,则∠DFC=∠BCF.所以,故①正确.
如图2,过F点作FG∥AE,则∠FGE=90°.又因点F是AD的中点,所以EG=CG,EF=CF,故②正确.
因为AB∥FG∥CD,且EF=CF,所以∠AEF=∠EFG=∠GFC=∠FCD=∠CFD,则∠DFE=3∠AEF,所以④正确.
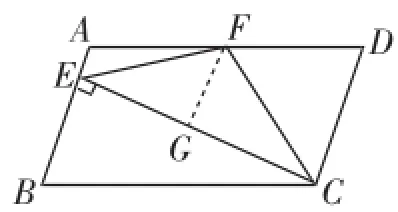
图2
赏析:本题作为一道填空题的压轴题,以学生熟悉的平行四边形为背景,通过“不定点E”的位置的变化探索相关的数量关系,需要综合运用平行四边形的性质、等腰三角形的性质与判定、平行线分线段成比例、直角三角形的相关性质等核心知识灵活解决问题,有效考查了学生对核心知识的理解及学生分析问题、解决问题的能力,综合性较强,有效承载了其应有的选拔和区分功能.但不可否认的是此题在表述上稍欠严谨或有待改进,题目表明“如图”,又强调垂足E在线段AB上,这样就给学生造成了少许的误导,点E可以与点A、点B重合,于是就有少数学生认为点E与点B重合时,B、E、C三点在一条直线上,构成不了三角形,故选项④也错误,类似的问题还出现在2015年中考数学卷的第12题.
例3(2013年)如图3,已知矩形纸片ABCD中,AB= 1,BC=2.将该纸片折叠成一个平面图形,折痕EF不经过A点(E、F是矩形边界上的点),折叠后点A落在点A′处,给出以下判断:
其中正确的是________.(把所有正确结论的序号填在横线上)

图3
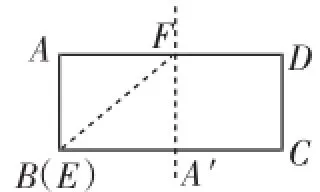
图4
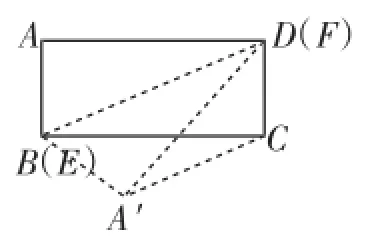
图5
解析:如图4,由四边形A′CDF为正方形,得A′F是矩形ABCD的中位线.所以AF=BA′=1.即点E与点B重合,EF即为正方形A′BAF的对角线.,故①正确.
如图5,当四边形BA′CD是等腰梯形时,只能是BA′= CD,EF与BD重合,所以,故④正确.
赏析:本题是近年来填空压轴题中区分度最小、难度最大的一道试题,不仅考查了正方形、矩形、轴对称、勾股定理等核心知识内容,又考查了学生动手操作探究、在开放的条件下分析问题、解决问题的能力.解决问题的突破口在于学生能否理解当折痕EF=时,折痕EF与矩形的对角线BD重合这一事实,难点是对A′C∥BD的理解与证明.另外从呈现形式上,四个选项两两独立,同时又以互逆的命题形式出现,命题专家独具匠心,使得试题的呈现漂亮、优美.
例4(2012年)如图6,P是矩形ABCD内的任意一点,连接PA、PB、PC、PD,得到△PDA、△PAB、△PBC、△PCD,设它们的面积分别为S1、S2、S3、S4,给出如下结论:
①S1+S2=S3+S4;②S2+S4=S1+S3;③若S3=2S1,则S4=2S2;④若S1=S2,则P点在矩形的对角线上.其中正确结论的序号是__________.(把所有正确结论的序号都填在横线上)
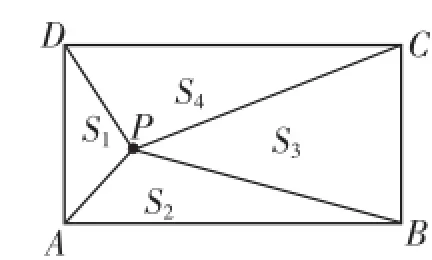
图6
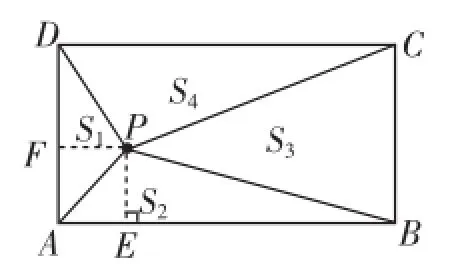
图7
解析:如图7,过点P分别作PF⊥AD于点F,PE⊥AB于点E,根据三角形面积公式结合矩形性质可得S1+S3=,同理可得,所以S2+S4=S1+S3,故②正确.
当点P在两条对角线的交点时,S1+S2=S3+S4,但P是矩形ABCD内的任意一点,所以该等式不一定成立,故①错误.
若S3=2S1,只能得出△APD与△PBC的高度之比,S4不一定等于2S2,故③错误.
若S1=S2,则,所以.由于四边形AEPF是矩形,所以矩形AEPF与矩形ABCD相似,则,所以P点在矩形的对角线上,故④正确.
赏析:本题主要考查三角形与矩形的面积计算及它们之间的转化关系、等式和不等式的性质等,此题看似简单,很多学生能认可事实,但却不知如何说理,作为多选题出现,既考查学生的直觉思维能力和合情推理能力,又避免了作为解答题带来的烦琐和复杂性,可见命题专家的良苦用心.另外,通过本题的解答还可得出矩形的两个“优美”性质.
性质1:设P是矩形ABCD内的任意一点,连接PA、PB、PC、PD,得到△PDA、△PAB、△PBC、△PCD,设它们的面积分别是S1、S2、S3、S4.若S1=S2或S3=S4,则点P在对角线AC上;若S1=S4或S2=S3,则点P在对角线BD上,反之亦成立.
性质2:设P是矩形ABCD内的任意一点,连接PA、PB、PC、PD,则PA2+PC2=PB2+PD2.
例5(2011年)定义运算a⊗b,下面给出了关于这种运算的四个结论:①2⊗(-2)=6;②a⊗b=b⊗a;③若a+b=0,则(a⊗a)+(b⊗b)=2ab;④若a⊗b=0,则a=0.其中正确结论的序号是_______.(填上你认为所有正确结论的序号)
解析:因为2⊗(-2)=2×[1-(-2)]=2×3=6,故①正确.
由于a⊗b=a(1-b)=a-ab,b⊗a=b(1-a)=b-ab,所以②错误.
(a⊗a)+(b⊗b)=a(1-a)+b(1-b)=a-a2+b-b2.又a+b= 0,所以原式=-(a2+b2)=-(a+b)2+2ab=2ab,故③正确.
因为a⊗b=a(1-b)=0,所以a=0不一定正确,故④错误.
赏析:本题是“新定义型”试题,是近五年来中考填空压轴题最为简单的一题,但其考查的知识点却非常丰富,不仅考查了实数运算、整式运算和配方法等内容,还渗透了数学的“整体思想”和“分类思想”,对开阔学生眼界、提高学生思维起到了一定的作用.
二、对2016年中考数学复习的启示
安徽中考数学卷多年坚守的多选题型填空题,虽在效度上有所欠缺,但考查容量大,解题思路广,数学思想丰富,甄别、选拔功能强,具有其他题型不具有的一些特点,预计2016年中考此类题型会继续存在,并延续一些相对稳定的现象特征.
1.强化数学核心概念、主干知识的复习
历年中考第14题,考查内容虽然侧重点有所不同,但以数学核心概念、主干知识为载体考查学生的数学素养及探究能力却是主旋律.如2015年中考卷第14题,初中阶段的方程(组)不管次数和元的个数,它们都是现阶段的核心概念,学生能顺利解决此题,熟练掌握方程(组)的解法“功不可没”,其他年份的第14题也是如此.由此可见,在中考复习中,要将核心概念、主干知识置于教学最重要的位置上,如在几何与图形内容上,重点引导学生复习直角三角形、等腰三角形、全等(相似)三角形、平行四边形及特殊四边形等基本图形的性质与判定,理解图形的平移、旋转和轴对称等重要概念并总结证明的思路、方法与技巧等.
2.重视数学活动经验的积累和数学思想方法的渗透
为回应《数学课程标准》“四基”要求,安徽中考卷第14题对数学基本活动经验和数学思想方法给予了高度的关注,如2013年安徽卷第14题除了考查部分核心知识,还对学生实际动手操作的活动经验进行了考查,对学生的思维能力要求较高,仅仅通过简单“题海战术”是无法完成此题的.再比如2015年安徽卷第14题,转化思想、分类讨论思想、方程思想、模型思想在本题中均有出现,这些都是初中阶段的核心数学思想.因此,在复习中,教师不要以解决问题作为教学的终结点,而应将数学思想方法的参透和数学活动经验的积累贯穿于全过程,使学生在学习基本知识的同时掌握数学思想方法,并通过不断的积累运用,内化为自己的知识经验.
3.引导学生关注合情推理与演绎推理的结合
从近五年安徽中考卷第14题分析不难发现,一般都是给出四个结论,其中有真命题、也有假命题,通常其中有两个结论学生通过直觉就能给出判断,而另两个结论相对要难一些,对考查学生的直觉思维能力、合情推理能力和演绎推理能力都起到了重要作用.如2012年安徽卷第14题选项①、③很容易通过画图找出反例,选项②通过演绎推理可快速得出,而对于选项④,用演绎推理很难得出正确结果,更多学生是通过画图,找不出反例,用直观感觉来判断.其实在分秒必争的考场,并不是所有问题的解答过程都需要书面呈现,有时只需在头脑中呈现,凭合理地“想”,也能取得不错的效果.所以在平时教学及复习时,要引导学生巧妙运用“图形反例”,结合合情推理快速、简洁地识别真(假)命题.
1.廖纯连.2015年安徽省中考数学试题总体评价及备课建议[J].中学数学教学,2015(5).
2.倪兴隆,夏敬花.从安徽中考卷窥探多选题型在数学能力测试中的作用[J].上海教育评估研究,2014(2).
3.高厚良.对2014年安徽中考数学卷第14题参考答案的质疑[J].中学数学(下),2014(10).
4.张宁.由一道中考题得出矩形的两个优美性质[J].中小学数学(初中版),2014(1-2).Z
