精心设计下的“别有洞天”——江苏省初中数学优质课的亲历及感悟

☉南师大附中新城初中怡康街校区李明顺☉南师大附中新城初中何君青

精心设计下的“别有洞天”
——江苏省初中数学优质课的亲历及感悟

☉南师大附中新城初中怡康街校区李明顺
☉南师大附中新城初中何君青

2015年11月，江苏省中小学教学研究室在淮安清江中学举办了江苏省2015年初中数学优质课评比活动，笔者有幸代表南京市参加比赛，荣获一等奖，在此过程中有颇多感悟和收获，故撰文与同行交流.

一、教学分析

本节教学内容选自江苏科学技术出版社义务教育教科书《数学（八年级上册）》第五章第一节“平面直角坐标系”.平面直角坐标系是在数轴的基础上发展起来的，它使点与数的关系从一维过渡到二维，使有序实数对与平面内的点建立了一一对应的关系，架起了“数”与“形”之间联系的桥梁.

在平面直角坐标系的相关概念得出时，很多教师这样操作：通过生活情境中的十字路口直接抽象出平面直角坐标系的模型，或者通过用实数表示数轴上的点过渡到平面内的点的表示方式.此处的做法，确实可以抽象出平面直角坐标系的概念，但教师“抛”的痕迹过重，学生的体会不深，更多的是一种感性的认识、粗浅的了解，不会真正理解建立平面直角坐标系的必要性.

在归纳坐标平面内的点与有序实数对一一对应的关系时，大部分教师都直接问两个问题：“在平面直角坐标系中，用有序实数对（a，b）描述一个点的位置，如果将这点记为点P，那么它的位置如何确定？”和“如果Q是平面直角坐标系中的一点，你能确定与它相对应的有序实数对吗？”，稍微好一点的老师会作一些铺垫，通过特殊到一般的过程让学生慢慢理解.此处的做法生硬、难懂，机械的训练，不会让学生感受到学习的乐趣，不会让学生认识到探索问题时的方法和策略，更不会让学生真正理解一一对应所蕴含的本质特征.

在得到象限的概念和归纳象限内的点的坐标的特点时，很多教师都会直接给出象限的概念，再通过几何画板拖动平面上一点的位置，让学生观察该点的坐标的变化后问：每个象限内的点的坐标的特点是什么？此处的做法真的是多媒体辅助教学好的例子吗？难道就不会限制学生思维的发展吗？难道在学生每次自主探索数学问题时都有几何画板作为工具吗？

基于上述考虑，笔者在设计本节课时，情境从学生熟悉的问题入手，让学生一开始“摸得到，看得着”，接着通过描述点P的位置体会建立平面直角坐标系的必要性，接着对其进行深入研究，通过从特殊到一般、具体到抽象的过程，体会建立平面直角坐标系后平面内的点与有序实数对一一对应的关系，继而将例题、活动中研究的所有点放在一起再次研究得出象限的概念及每个象限内的点的坐标的特点，最终达到经验的迁移、能力的提升.

二、教学片段

片段1：开篇情境，渗透对应

师：同学们，今天老师第一次给大家上课，对大家并不熟悉，如果课堂上我想有针对性地请某位同学回答问题，你能帮老师设计一个简单、可行的办法吗？例如我想请这位帅气的男生回答问题.

生1：可以说他的位置，例如第三列第二排.

师：（转向那个帅气的男生）你同意我这样叫你吗？

生2：同意.

师：能用一种简单的方式记录吗？

生3：（3，2）.

师：其实，这样的形式小学时就学过，当时称为数对，逗号能省略不写吗？

众生：不能.

师：两个数的顺序能交换吗？

众生：也不能.

师：为什么？

生4：因为交换位置，就表示第二列第三排了.

师：确实，它是有顺序的，数学上将这样有顺序的数对称为有序实数对.现在我报一对有序实数，能有一个同学站起来吗？（5，4）.

生5：是我！

师：（3，5）.

生6：是我！

师：看来，教室里有一个对应的关系！

分析：一改惯用的复习旧知识、引入新课的手法，从学生熟悉的生活实际出发，设计一个引人入胜的生活情境，让学生获得成功的经验，消除刚上课的不适应感，并对小学曾经学过的数对加深认识，提出有序实数对的概念，通过报数对让学生站起来的过程，使学生感受教室里存在着一个对应的关系，但生活情境又不过多地加以研究，适可而止，不让生活冲淡数学，为接下来建立平面直角坐标系、发现平面内的点与有序实数对一一对应作铺垫.

片段2：连贯活动，体会对应

活动一

师：将具体问题抽象成数学问题，你能描述点P所在的位置吗？（如图1，为了让同学看得更直观，老师在黑板上制作一个类似的模型）

图1

生7：右上方.

师：能理解这3个字的请举手.（部分学生举手）能帮我解释一下，所谓的右是什么？所谓的上是什么？

生8：要在黑板上先画两条直线，一条水平直线，一条垂直直线.

师：（根据学生的描述画出两条相互垂直的直线）有了这两条线作为参照，右上方好理解了，但右上方的点只有这一个吗？

生：不是.

师：你能更精确地描述点P所在的位置吗？

生9：在两条直线上标上刻度，再过点P作两条直线的垂线，是有序实数对表示.

师：（根据学生的描述进行相应的操作）能描述点P所在的精确位置吗？

生10：（3，2）.

师：再给你一点Q（课前在黑板上确定好大概位置，使P、Q两点关于铅直直线对称），你能精确地描述点Q所在的位置吗？

生11：和之前一样的方法，（教师操作完成后）可以记为（-3，2）.

师：（继续追问）（-3，2）？这里的-3从何而来？

生11：将左边记为负数，不就是-3了？

师：（继续追问）灵感从何而来？

生11：数轴.

师：非常好，有了这个参照物，就能精确地描述点P和Q的位置了，观察一下，说说你对这个参照物的认识.

生12：它由两条数轴组成，而且是垂直的.

师：观察的很仔细，有了它就可以统一管理平面内的所有点了，数学上将其称为平面直角坐标系，今天就来学习它.（之后介绍平面直角坐标系相关概念）

分析：将具体问题抽象成数学问题，生活的经验让学生能很快地回答，通过教师一步一步的追问，让学生体会到建立参照物（平面直角坐标系）描述点P的位置的必要性，再通过点Q的追问，构建出平面直角坐标系的雏形，通过“提出问题—构建参照物—说一说对参照物的认识”的过程，让学生亲身经历概念形成的全过程，感受数学概念形成的自然性与合理性，加深学生对平面直角坐标系概念的理解.

活动二

师：现在给你一点A（在黑板上任意点出一点），你能精确地描述它所在的位置吗？

生13：（-2，-3）.

师：（继续追问）为什么？

生13：过点A分别作x轴、y轴的垂线，将垂足对应的实数组合起来形成一对有序实数，所以是（-2，-3）.

师：再给出一点B，请你精确地描述它所在的位置.

生14：（1，-2）.类似地，过点B分别作x轴、y轴的垂线，将垂足对应的实数组合起来形成一对有序实数，所以是（1，-2）.

师：若我残忍地将平面直角坐标系擦掉，请看幻灯片（幻灯片和黑板上的点的位置一样，但瞬间幻灯片上的平面直角坐标系消失了），对于这四个点，还能像之前一样精确地描述它们所在的位置吗？

生：不能.

师：看来，平面直角坐标系真的很伟大，没有它，点只不过是一个普通的点，有了它就不一样了，还是将它复原回来吧，想一想，平面直角坐标系到底起到了什么作用？

生15：有平面直角坐标系就好描述位置了.

师：（继续追问）描述什么的位置？

生15：点.

师：（继续追问）用什么描述的？

生15：有序实数对.

师：也就是说，有平面直角坐标系平面内的点就能用有序实数对表示了（将其记录在黑板上）.

分析：第一个点的作用：既可帮助学生巩固之前的描述方法，又是用有序实数对表示点的开始，第二个点的作用是让学生巩固用有序实数对来表示点.教师配合幽默的语言，擦掉平面直角坐标系和复原平面直角坐标系的过程，让学生迅速感知到建立平面直角坐标系后，平面内的点可以用有序实数对来表示.

师：再给出一点C，你能写出与它相对应的有序实数对吗？

生16：（3，-1）.

师：更一般地，如果Q是平面直角坐标系中的一点，你能确定与它相对应的有序实数对吗？

生17：过点Q分别作x轴、y轴的垂线，将垂足对应的实数组合起来形成一对有序实数.

分析：此处的问法和之前不同，从“你能精确地描述它的位置吗？”转换成“写出与它相对应的有序实数对”，上升到规范的语言，进一步让学生掌握在平面直角坐标系中由点的位置写出与它相对应的有序实数对的方法.

师：反过来，又会怎么样呢？带着疑问一起研究.若给出一对有序实数（3，2），你能在平面直角坐标系中，确定一个与它相对应的点D吗？

生18：（上黑板画好后再回答）过x轴上表示3的点画x轴的垂线，再过y轴上表示2的点画y轴的垂线，两条垂线的交点即为点D.

师：看一看，是不是和P点重合了（学生点头），看来数对（3，2）确定了，画出的点是一样的.再给出一对有序实数（-2，4），你能在平面直角坐标系中，确定一个与它相对应的点E吗？

生19：过x轴上表示-2的点画x轴的垂线，再过y轴上表示4的点画y轴的垂线，两条垂线的交点即为点E.

师：通过这个活动，你发现了什么问题？

生20：有了平面直角坐标系后，一对有序实数可以确定一个点的位置.

师：看来之前的疑问解决了，更一般地，在平面直角坐标系中，用有序实数对（a，b）描述一个点的位置，如果将这点记为点P，那么它的位置如何确定？

生21：过x轴上表示实数a的点画x轴的垂线，再过y轴上表示实数b的点画y轴的垂线，两条垂线的交点即为点P.

分析：话锋一转，研究新问题，由于学生首次接触在平面直角坐标系中根据有序实数对画点，故需进行适当的铺垫，让学生经历由特殊到一般、具体到抽象的过程，使学生初步感知到建立平面直角坐标系后，一对有序实数可以确定一个点的位置.

活动三

师：回顾整个过程，一共总结出了两句话，你能合起来说一遍吗？

生22：在平面直角坐标系中，一对有序实数可以确定一个点的位置；反过来，任意一点的位置都可以用一对有序实数来表示.简单点说就是建立平面直角坐标系后，平面内的点与有序实数对一一对应.

师：非常好.（介绍坐标的概念）

【设计意图】通过之前环环相扣的联系，快速让学生归纳出一一对应的概念，而且十分自然，学生也有很深刻的理解，彻底攻破本节课的难点.

片段3：活动串联，产生新知

师：运用一下，做个例题：在平面直角坐标系中，

（1）画出点F（3，1）、G（0，-4）；

（2）写出点M、N的坐标.

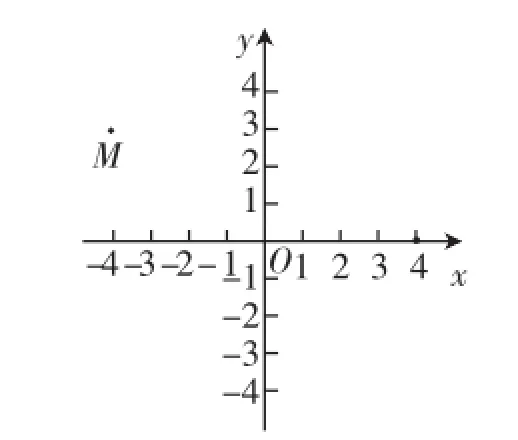
图2

师：将活动和例题中的11个点放在一起来研究（活动和例题的点都在研究的过程中在黑板上呈现出来），你可以给这些点分分类吗？

生23：可以按照右上方的点、右下方的点、左上方的点、左下方的点、坐标轴上的点将其分类.

师：看来需要给这几个区域起个名称了，叫起来才更方便.两条坐标轴将平面分成的4个区域称为象限，按逆时针顺序分别记为第一象限、第二象限、第三象限和第四象限.由于坐标轴是象限与象限之间的分界，因此坐标轴不属于任何象限.

师：现在，我报几个点的坐标，你能迅速判断出它所在的位置吗？（5，6），（-3，1），（-2，-3），（0，5），（-2，0）.（学生快速回答）

师：同学们真聪明，你们是怎么这么快回答出我的问题的？

分析：通过这个环节，让学生从另一个视角再认识前面的问题，初步培养学生规范化的表达，让学生感受不同象限内的点的坐标的不同之处，之后通过几个快速回答，“逼”出学生模糊的认识：平面直角坐标系各象限内的点的坐标的符号特点及坐标轴上点的坐标的特点.

片段4：篇末呼应，精彩生成

师：通过今天的学习和研究，你对平面直角坐标系有了哪些认识？（喊2-3名同学回答）

师：看来，今天着重研究了平面内的点，若让你继续研究，你还有什么想研究的吗？

生24：空间内的点怎么研究？

生25：有了平面直角坐标系，点可以用有序实数对表示，那么线怎么表示呢？

生26：如果平面坐标系不是直角，还能精确地描述点的位置吗？

分析：建立平面直角坐标系的初步目的是将平面内的“形”与“数”结合起来，但最终目的是用它的思想方法解决更多的问题，达到经验的迁移、能力的提升，从而学以致用、学有所用.故此处也是拓展延伸处：“你还有想研究的问题吗？”让学生主动地提出问题、发现问题、分析问题、解决问题.此处不仅仅是单纯的知识罗列，应该是画龙点睛之笔，承前启后，适当外延，是对整堂课学习的一个提升.

三、教学反思

本节课的授课内容属于规则下的概念课教学，与其他概念课不同的是本节课的概念可以看作是一个概念群，多而细，所以教学时要逐步让学生理解相应概念，不能操之过急.

本节课的亮点有3处：其一注重设计问题串，引领学生思考探究，促进数学理解，典型的是一一对应的教学处，环环相扣，擦掉平面直角坐标系的过程更是“逼”出了学生思维中对平面直角坐标系的认识；其二在注重一节课的连贯性，首尾呼应，让学生帮忙设计的喊学生的方法贯穿整节课，活动中的点和例题中的点最后归为一处又成为一个新探究；其三在最后的小结处，让一节课的精彩升华到最高点，大胆鼓励学生自己提问题，而且个个问题堪称经典.

纵观本节课精心设计下可谓“别有洞天”.

1.以活动为主线

本节课的教学中，以学生作为活动的主体，注重知识的发生、发展，让学生通过一个个活动感受到了学习新知识的必要性和迫切性.

片段1从学生熟悉的生活情境入手，贯穿一节课.片段2活动一从数学背景切入，凸显出建立平面直角坐标系的必要性，活动二环环相扣，通过从特殊到一般、具体到抽象的过程，让学生归纳出在给定的平面直角坐标系中，根据点的坐标描出点的位置，由点的位置写出点的坐标的方法，初步感受建立平面直角坐标系后，平面内的点与有序实数对一一对应的关系，活动三是对难点的再认识，进一步感受建立平面直角坐标系后，平面内的点与有序实数对一一对应的关系，最终与例题结合再次研究每个象限内的点的坐标的特点.3个活动可谓用“足”、用“透”，以活动开始，以活动结束，贯穿整堂课.

2.以方法为支撑

课堂上，只有让学生真正“动”起来、“活”起来，才能让学生成为课堂学习的主角，学生的学习热情才会高涨，创造力才会加强.所以在教学本节课时，笔者语言精炼，个个问题都简洁、精炼，尽可能让学生多说、多做、多悟，让学生充分体会概念的形成过程，力求达到“概念的得出是水到渠成的、自然的，而不是强加于人的”的教学境界.

3.以思想为灵魂

本节课最主要的数学思想就是数形结合思想，而在整节课的教学中，笔者很少提及抽象的“数”、“形”二字，取而代之的是用通俗的语言与学生交流，慢慢渗透“数”与“形”的关系，尊重了学生的认知规律.

4.以能力为归宿

荷兰数学家弗莱登塔尔提出：学习数学唯一正确的方法是实行“再创造”，也就是由学生本人把要学的东西自己发现或创造出来.本节课中笔者多次给予学生发现、创造的机会，如片段2描述点P的位置，让学生体会构建参照物描述点P位置的必要性，创造出平面直角坐标系的雏形，在片段4中，让学生尽情地说，提出一个又一个精彩的问题，如“空间内的点如何描述”，充分给予学生思考、比较、类比、抽象、概括等一系列能力提升的机会.Z