四基为本方法为脉思想为魂
——“有关矩形的折叠问题”专题复习的教学设计
2016-09-21浙江省宁波市鄞州实验中学蔡卫兵
☉浙江省宁波市鄞州实验中学蔡卫兵
四基为本方法为脉思想为魂
——“有关矩形的折叠问题”专题复习的教学设计
☉浙江省宁波市鄞州实验中学蔡卫兵
“专题复习”是中考备考过程中教师们普遍采用的复习手段,也是中考复习备考的重要环节.其核心教育价值不仅在于促进学生对数学思想认识的深化,更在于促进学生在数学活动经验中的飞跃生长和发展.因此,在进入专题复习阶段,专题的选编要以四基为本,回归教材,突出重点,渗透考点,实现对知识的重新、有效的整合;要以方法为脉,串联考点,变式引申,实现对通性通法的灵活掌握;要以思想为魂,类比联想,推理运算,贯穿始终,实现对基本活动经验的积累,从中培养学生思考问题的灵活性、开拓性、多向性和创造性,收到以少胜多、事半功倍之效.本文以“有关矩形的折叠问题”专题复习的教学设计为例,谈谈如何以点带面,一图多折,展开以一题多解、一题多变为主要形式的训练,让学生获得感性知识、情感体验和应用意识等具有发展性的经验认识.
一、四基为本,揭示折叠本质
问题1:如图1,在矩形纸片ABCD中,AB=8,BC=6,将△ABD沿对角线BD折叠,使点A落在点E处,BE与CD交于点O,AE与BD交于点F,在折叠过程中你能得到什么结论?
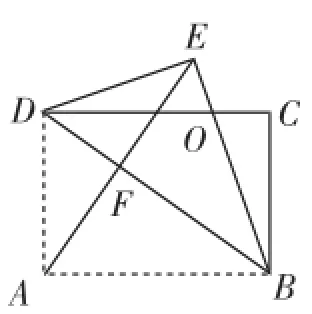
图1
生1:DE=DA,BE=BA,∠BED=90°,∠EDB=∠ADB,∠EBD=∠ABD.
师:根据折叠前后的两个图形是全等图形可得到上面的直接结论.
生2:BD垂直平分AE.
师:很好地抓住折叠前后的对应点关于折痕对称,折叠的本质就是轴对称变换.
生3:△DOE≌△BOC,OE=OC,OD=OB;△ABF∽△DAF∽△DBA.
师:这是根据全等三角形和相似三角形的判定和性质得到的间接结论,通过简单的逻辑推理而获得.那你根据条件所给出的具体数据能计算出哪些量呢?
生4:矩形ABCD的周长和面积,△ABD的周长和面积,∠ABD的三角函数值,还有利用面积法求出AF=,利用相似三角形或锐角三角函数或勾股定理求出BF=,应该是图中所有线段的长都可以求出.
师:请说说线段OE的长如何计算?
生5:设OE=x,根据△DOE≌△BOC,可得OC=x,则OD=8-x,在Rt△DOE中,由勾股定理得x2+62=(8-x)2,解得x=.
师:很好地运用了方程的思想来解决问题,关于线段长度的计算经常会放在直角三角形中利用勾股定理加以考虑.
生6:根据生5求得的结果进一步可求出△DOE、△BOC、△BOD的周长和面积.
师:很好,中考中有关折叠问题除了线段的计算还经常会涉及图形的周长和面积的计算,做了很好的迁移和推进,如果不求出线段OE的长,那么能否求出△DOE的周长呢?
生7:因为OE+OD=OC+OD=CD=8,所以OE+OD+DE= 14,即△DOE的周长为14.
师:很好地运用了符号化的换元思想和整体思想来解决问题.
评析:“四基”是学生学习数学的基础,是发展数学能力的保证,没有扎实的基础,发展能力就成为空中楼阁、无源之水、无本之木.此题以对角线为折叠线设计一个开放性问题,让学生体验折叠前后的两个图形是全等的,理解折叠的本质就是轴对称变换.同时在凸显图形之间的内在联系的过程中,复习回顾全等三角形、相似三角形、勾股定理、锐角三角函数等核心知识,进一步感悟方程思想、整体思想、模型思想等在解决几何问题中的应用.
二、方法为脉,探求通性通法
问题2:在矩形纸片ABCD中,AB=8,BC=6,P为AD边上一点,将△ABP沿BP折叠,使点A落在点E处.
师:如果不沿对角线折叠,新图形中的未知线段是否还可以求出?请大家先思考当点E在CD边上的情形,求AP的长.
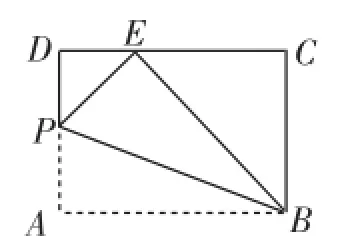
图2
生9(补充):借助勾股定理所列方程,解起来比较麻烦.先证明△DEP∽△CBE,所以,即EP=
师:因为∠C=∠D=∠BEP=90°,这是一线三等角模型,很好地运用了模型思想来解决问题,关于线段长度的计算经常会放在两个相似三角形中利用对应边成比例加以分析.
生10(补充):通过正弦函数建立线段之间的关系,因为∠DPE=∠CEB,所以sin∠DPE=sin∠CEB=,即,所以
师:事实上关于直角三角形问题,利用相似性质得到的对应线段成比例与利用三角函数得到的线段比例关系本质上一样的,相似与三角函数是沟通线段之间关系的重要工具,也是求线段长度的一种常用方法.

图3
生11(补充):因为点A与点E关于直线BP对称,所以BP垂直平分AE(如图3),易证∠DAE=∠ABP,所以Rt△ADE∽Rt△BAP,所以,即
生12(补充):通过正切函数建立线段之间的关系,因为∠DAE=∠ABP,所以tan∠DAE=tan∠ABP,即,所以
师:若点E在BD边上(如图4),你还能求出AP的长吗?
生13:(方法一)在Rt△DPE中,由勾股定理列方程可求出AP.
(方法二)借助相似基本图形,由△DPE∽△DBA的对应边成比例可求出AP.
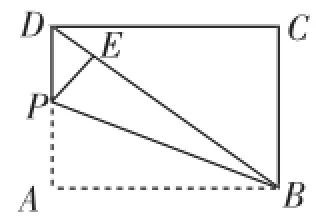
图4
生14(补充):面积法,由S=S+S得
△DAB△DPB△APB2,进而求出AP.
师:若点E在CD的上方(如图5),PE与CD相交于点O,OE=OD,你还能求出AP的长吗?
生15:因为OE=OD,∠D=∠E= 90°,∠DOP=∠EOF,所以△DOP≌△EOF,所以OP=OF,所以OP+OE=OF+OD,即PE=DF.设AP=x,则DF=PE=x,CF=8-x;EF=DP=6-x,BF=x+2.在Rt△CBF中,由勾股定理得(8-x)2+62=(2+x)2,解得x=.
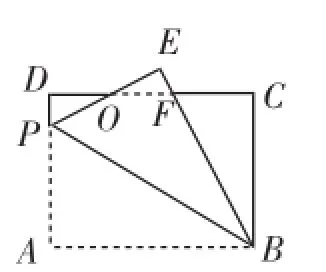
图5
评析:根据学生的认知规律,以“问题串”的形式引导学生积极开展数学思维活动.从对角线为折叠线到过一顶点所在的直线为折叠线,从折叠后的落点在边上到对角线上再到一般位置,观察数量及数量间的关系、图形及图形间的关系,以及数量和图形间的关系,通过“异中求同”或“异中观同”来抓住本质和共性,进一步挖掘折叠问题的内在价值.在问题解决过程以寻找等量关系、渗透方程思想为一条清晰的主线,涉及的知识有勾股定理的应用,通过三角函数值建立比例式,借力一线三等角模型、三垂直模型、母子相似模型寻找相似三角形,利用三角形面积法列方程求解,让学生养成多角度去分析问题和解决问题的思维习惯,不断提升学生的思维深度,逐渐形成能力.
三、思想为魂,拓展思维空间
问题3:如图6,在矩形ABCD中,AB=8,BC=6,M、N分别为边CD、AB上的点,将四边形ADMN沿MN翻折至四边形EFMN,点E在BC边上,且BE=4,求DM的长.
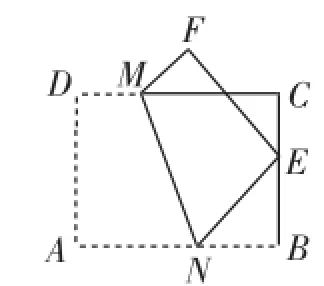
图6
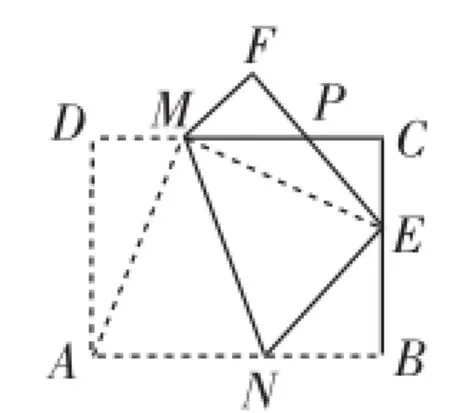
图7
师:这个问题的折叠线有什么特点?与上面有什么不同?
生16:折叠线的两个端点在对边上,这时要关注两个顶点的落点,前面问题的折叠线的两个端点在相邻边上,往往只需关注一个顶点的落点.
师:有关矩形折叠问题,折叠线有两类,很好地运用了分类思想考虑问题,同时指出了这时应要关注两个顶点的落点,那你会先分析哪一个呢?
生17:因为点A落在BC边上的点E处,这个位置比较特殊,而且这种情形上面已解决过,而点D的落点F比较一般,所以先分析点A及其落点E.
师:你是运用了特殊到一般的思想考虑问题,同时又将新的问题转化为已经解决的问题,运用了转化思想.那你能通过转化、类比等数学思想方法解决这个问题吗?
生18:在Rt△NEB中,根据勾股定理运用方程思想得NB=3,NE=5.设EF与CM交于点P(如图7),根据一线三等角模型得△PCE∽△EBN,由此求得.再由△PMF∽△PEC,求得,所以DM=2.
师:真的太厉害了,转化、类比思想能灵活运用,同时又结合方程思想和模型思想加以解决问题.大家继续交流探究,还有其他解法吗?
生19:同上得NB=3,NE=5,连接AM、EM(如图7),设DM=x,则CM=8-x,在Rt△DMA中,由勾股定理得AM2= x2+36,在Rt△MCE中,由勾股定理得ME2=(8-x)2+4,根据MA=ME,得x2+36=(8-x)2+4,解得x=2.
生20:同上得NB=3,NE=5,连接AE,过点M作MH⊥AB于点H(如图8),由三垂直模型得△MHN∽△ABE,所以,所以NH=3,AH=2,从而由矩形ADMH得 DM=AH=2.
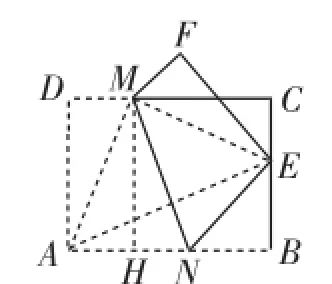
图8
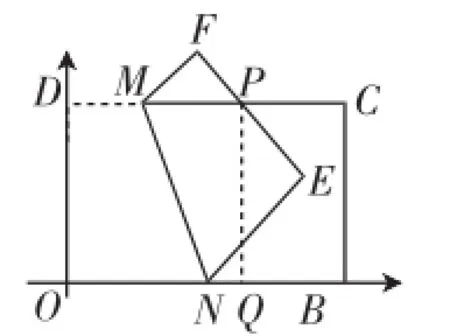
图9
生21:连接MA、ME、AE,过点M作MH⊥AB于点H(如图8),在Rt△ABE中,由勾股定理求得,由三垂直模型得△MHN∽△ABE,所以,所以,NH=3.所以四边形MANE的面积为MN·,由面积法得30,所以AN=5,AH=2,从而由矩形ADMH得DM=AH=2.
师:若将矩形放置在平面直角坐标系中,如图9,矩形OBCD置于平面直角坐标系中,M、N分别为CD、AB上的点,将四边形ODMN沿MN翻折至四边形EFMN,已知点C(m,6),点E为(8,4),求DM的长.
生(众):此题与上题一模一样,过点P作PQ垂直OB,可将此题转化为上题,连数据都一样,所以可得DM=2.
评析:专题复习是一个经历从量变到质变的快速累计阶段,在思想上应突出关注.数学思想方法比数学知识更抽象,思想方法的教学是一种数学活动的过程,重在领会应用,学生的参与显得尤其重要.此题的设计在前面的基础上,将问题背景复杂化,折叠线的两个端点在对边上,从而将三角形翻折变化到四边形翻折,从关注一个落点到考虑两个落点,在理解题意中体验折叠线与落点的分类思想,在寻找突破口,确定思维起点中感受转化思想、特殊到一般思想,在明晰思路、解决问题中领悟几何直观、模型思想、方程思想、类比思想,在问题变式中运用转化思想,将数学思维方式融合到对具体问题的探究之中.
专题复习课的难点多、运用的数学思想方法多,而如何将解决问题的策略与思想方法让学生领悟到,这是教学的难点;如何做到既能全面系统地复习,又能提高学生的综合能力是值得探究的问题.所以,在选题设计上,寻找和挖掘问题内涵是关键,注重方法串联的题组学习,强调数学思想的主体突出;在讲题实施上,在特殊处思考,找到解题的切入点,发展从特殊到一般的归纳思维经验,以及识别基本模型的转换思维,教师应注意对问题的结构思考,在问题变式中完善经验.以“四基为本,方法为脉,思想为魂”的专题复习,可使学生在获得较系统的数学知识的同时,学会思维策略,进而培养学生灵活运用知识去解决综合问题的能力.
1.刘安清.如何让中考专题复习更“专”[J].中国数学教育(初中版),2015(12).
2.刘永东.谈2015年中考数学专题复习[J].中国数学教育(初中版),2015(12).
3.朱建良.折在关键叠在本质——折纸问题的探究性教学[J].中学数学教学参考(中),2014(5).
4.商庆平.让数学基本思想与基本活动经验生长在学习支架上[J].中学数学教学参考(中),2013(3).H
