预设铺垫问题：难题讲评用力点

2016-09-21江苏省泰州市姜堰区实验初级中学孔忠娣

中学数学杂志 2016年10期

☉江苏省泰州市姜堰区实验初级中学孔忠娣

预设铺垫问题：难题讲评用力点

☉江苏省泰州市姜堰区实验初级中学孔忠娣

在最近一次中考模考测试中，我们改编了一道把关题，不少学生对第二、三问显示出不太适应的状态，为了追求较好的讲评效果，我们对这两问进行了认真准备，特别是预设了大量的铺垫问题，取得了较好的讲评效果.本文先呈现该题的思路突破，并给出跟进的教学设计，与大家分享交流.

一、模考题与思路突破

模考题：如图1，平面直角坐标系中，抛物线y=x2+bx+ c与x轴交于A（-1，0）、B（3，0）两点，与y轴交于点C，该抛物线的顶点为D.

（1）求b、c.

（2）设点M在x轴下方的抛物线上，当∠ABM=∠CBD时，求出点M的坐标.

（3）以OB为边在第四象限内作等边△OBP.设点N（n，0），且n＞1，连接PN，把线段PN绕点P顺时针旋转60°得PE，求线段DE的长的最小值.

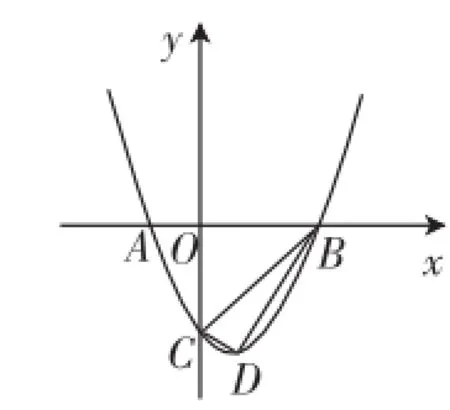
图1

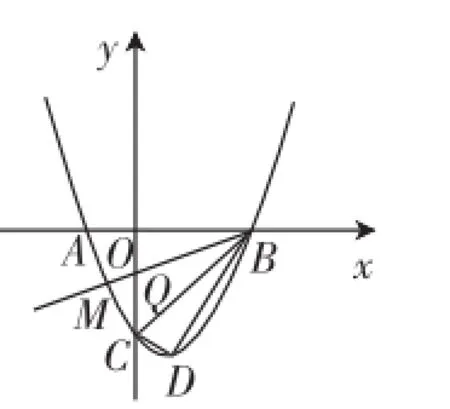
图2

思路突破：（1）把点A、B的坐标代入y=x2+bx+c中，可求出b=-2，c=-3.

（2）这个小问的起点是首先分析△BCD的形状，可以计算出BC、CD、BD的长，根据勾股定理逆定理发现∠BCD为直角，于是，此时若在y轴上取一点Q（0，-1），如图2，作射线BQ交抛物线于点M，则点M就是符合要求的（满足∠ABM=∠CBD）.进一步再求点M的坐标时，可以先分析出直线BQ的解析式为，再把与y=x2-2x-3联立，可解出点M的坐标

（3）先读懂题意，然后分离图形、排除干扰，如图3，基于“一线三等角”的模式经验，构造△OPN≌△KNE，可得KE=ON=n，再过点E作EH⊥x轴于点H，过点D作 DG⊥EH于G点，可以用含n的式子表示出，进一步在Rt△DEG中利用勾股定理表示出，化简得，由二次函数的性质可分析出：当n=2√3-1时，DE2有最小值7+4√3，相应地，DE有最小值2+√3.

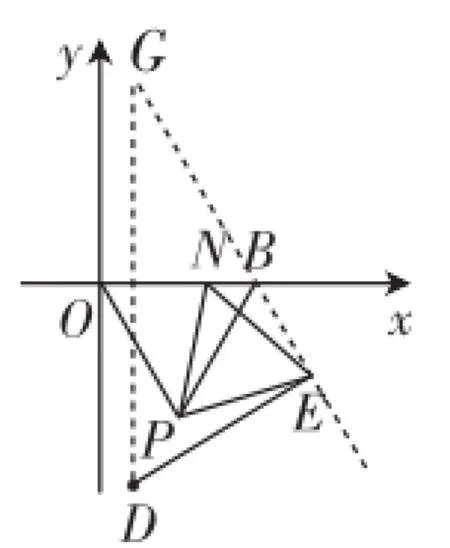
图4

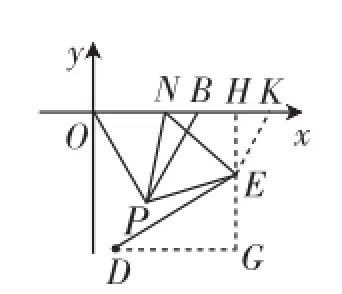
图3

另解分析：如果上述解法在构造上显得较为繁杂，并且对于数式变形要求也太高的话，有理由让我们重新寻找问题的结构.如图4，连接BE，可证△PON≌△PBE，得出∠PBE=∠PON=60°，即点E的运动轨迹在一条直线（直线BG）上！这很关键，此时点D到E的距离的最小值就是点D到直线GE的距离.过点D作DE⊥BG于E点，此时△DEG是一个含30°角的直角三角形，容易求出DG=4+ 2，于是DE=2+.

二、模考题讲评的教学设计

考题呈现：如图1，平面直角坐标系中，抛物线y=x2+ bx+c与x轴交于A（-1，0）、B（3，0）两点，与y轴交于点C，该抛物线的顶点为D.

问题1：能确定该抛物线的解析式吗？你有哪些不同的方法？

问题2：求证△BCD是直角三角形.

问题3：求tan∠CBD的值.

问题4：若在y轴的负半轴上有一点Q，且∠ABQ=∠CBD，求直线BQ的解析式.

问题5：若在x轴的下方，抛物线上有一点P，且∠ABP=∠CBD，求点P的坐标.

问题6：以OB为边在第四象限内作等边△OBP，求点P的坐标；

问题7：设点N（n，0），且n＞1，连接PN，把线段PN绕点P顺时针旋转60°得PE，有人认为点E一定在某直线上，你觉得呢？

问题8：在上一问的条件下，连接DE，DE是否有最小值？如果有，求出最小值；如果没有，请说明理由.

问题9：有同学构造出图3，在Rt△DEG中利用勾股定理表示出DE2，你知道他是如何分析的吗？

预设意图：“问题1”对应着模考题的第一问，“问题2～5”对应着模考题的第二问，“问题6～9”对应着模考题的第三问，试图通过系列问题的驱动，引导学生更好地思考把关题，并自主获得问题的解答.

讲评之后，再给一道简单变式后的跟进再练.

变式再练：如图5，已知抛物线y=x2-2x-3与x轴交于A、B两点（点A在点B的左侧），与y轴交于点C，该抛物线的顶点为D，对称轴交x轴于点G.

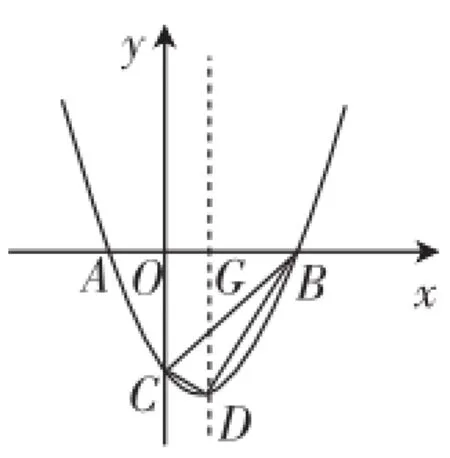
图5

（1）求A、B两点的坐标.

（2）求证：△BCD是直角三角形.

（3）设点P在x轴下方的抛物线上，当∠ABP=∠CDB时，求出点P的坐标.

（4）以OB为边在第四象限内作等边△OBM.设点E为x轴的正半轴上一动点（OE＞OG），连接ME，把线段ME绕点M顺时针旋转60°得MH，试分析∠DBH的大小是否变化，并说明理由.

（5）在（4）中条件下，求线段DH的长的最小值.

三、进一步的思考

1.难题讲评重在预设铺垫过渡问题

我们见过有些试卷讲评课，由于教师仅仅满足于自己解题或思路贯通就开展解题教学，使得学生在关键处、障碍处仍然没有得到有效的突破，讲评时的重点不够突出，讲评过程略显平均用力，使得讲评效果不太理想.基于上述认识，我们认为对于较难习题的讲评，教师备课的重点应该是精心设计铺垫问题或引导问题，下面截取一张我们在讲评时的PPT图片（如图6），有利于大家了解我们是如何渐次呈现系列追问的.

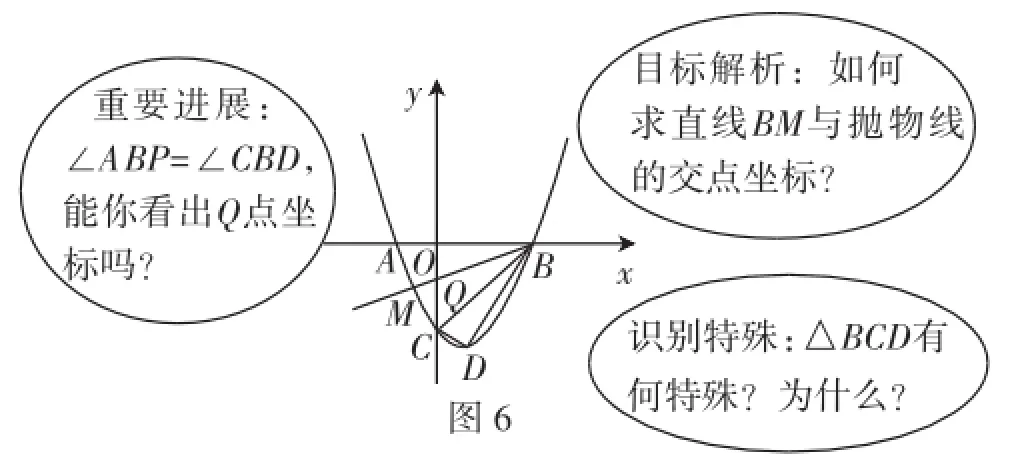
2.回顾反思重在揭示问题深层结构

数学较难问题的求解不能满足于一种解法，带领学生思考多种解法是必要的，更为重要的是思考多种解法的和谐与一致，即“殊途何以同归”.从模考题的第三问来看，使用第一种方法获得思路之后，仍然需要思考为什么有这样的答案，通过“数式变形”算出来的结果如何获得直观上的确认？这就有了我们关于该问题的另一种方法，即引导学生发现点E的运动轨迹是一条直线！

3.通过变式再练有效提高讲评实效

根据多年习题讲评的教学经验，对于较难问题通过讲评一次就能懂的学生不会超过三分之一，近三分之二的学生需要有跟进的变式再练，所以为了提高这类难题的讲评效果，我们倡导对所讲评的习题简单改编后再让学生练习，这也是我们在上面提供的教学设计最后附上变式再练题的原因.这里值得一说的是两点，第一，变式的距离不能太大，一般设计成4～5个小问，其中前4个问题都要严格对应讲评过程中提到的问题结构的解法关键；第二，最后一问也可以适当拓展或生长，给少数优秀学生提供挑战、向上的机会.