教材习题微改编的操作与实践
2016-09-21浙江省宁波市奉化市剡溪中学范锦君
☉浙江省宁波市奉化市剡溪中学范锦君
教材习题微改编的操作与实践
☉浙江省宁波市奉化市剡溪中学范锦君
波利亚指出:“拿一个有意义但又不复杂的题目去帮助学生发掘问题的各个方面,使得通过这道题就好像通过一道门户,把学生引入一个完整的领域.”教材习题显然符合这样的特点,它具有典型性、可延伸性,或传递某种数学方法,或渗透某些数学思想,或揭示某个数学结论,其重要性不言而喻.目前教材习题的设置往往适切于本章或本节教学内容,形式上比较单一,缺乏“一点多式”“一题多变”的灵活性,难以满足不同学生在数学上的不同发展.近年来,很多学业考试的试题改编自教材习题,因此,对它们不能停留于就题论题,而应根据学生实际情况进行适当改编即微改编,围绕其核心价值部分进行引申、挖掘.这样不仅能产生触类旁通、举一反三等让习题增值的效果,而且能开阔学生的思路,培养学生的创造力.
改编教材习题首先要解决的是习题源的选择问题,教师可以结合教学实际,选取基础性好且有良好发展空间可塑性强的习题.那么,如何进行习题的微改编呢?这里笔者将习题改编着眼于教师易操作、入手快的微改编上,通过几年的实践,探索形成了“一拆三变”微改编策略,供读者参考.这种改编方法的要点是先将习题源拆分为条件与结论两部分,然后运用三种变换方式得到一系列新试题.具体操作如下所示.
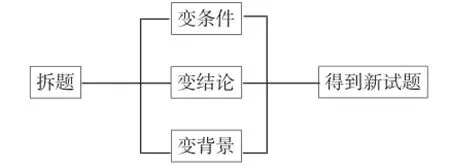
变条件即通过强化、弱化条件或者条件与结论置换,拓展知识的深度和广度;变结论即改变或转换设问的考查目标、呈现形式(如开放、探究式)与习题题型,纵向挖掘,横向发展,增强思维的灵动性和深刻性,理清知识之间的相互联系;变背景即改换图形、情境等,追求知识本质的理解和提升学生的建模能力.这样通过先拆后变的改编方法在原题的邻近区域内产生新试题,使原题达到化熟为生、化生为熟的效果.
一、变条件
例1如图1,在四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点.求证:四边形EFGH是平行四边形.
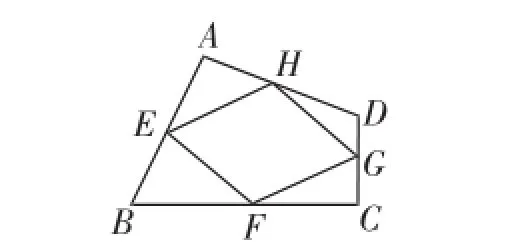
图1
本题是浙教版课标教材八年级下册“4.5三角形的中位线”中典型的四边形与中位线结合的习题,为后续学习矩形、菱形、正方形等相关试题起到了很好的“水龙头效应”.在教学过程中,很多教师并没有真正挖掘其习题功能,更多的是通过增加对角线条件使其逐步特殊化.当然如此处理不可谓不好,对于理清几种特殊四边形的判定方法应该是很有帮助的,但始终感觉缺乏对学生思维能力的提升.笔者将本题的“中点”这一条件逐步弱化,尝试作了如下改编.
问题1:已知E、F、G、H分别是四边形的边AB、BC、CD、DA上的点,且不是中点,能否使四边形EFGH仍为平行四边形?
如图2,在AB上任取点E(E不是AB的中点),过E分别作EF∥AC,EH∥BD,F、H分别在BC、AD上,过F作FG∥BD,G在CD上,连接GH.由 EF∥AC,EH∥BD,FG∥BD,分别得,从而得,于是可得GH∥AC.这样就证明了四边形EFGH为平行四边形.

图2
由于E是AB上任意一点,因此问题1中的平行四边形EFGH有无数个,那么在这无数个平行四边形中,能否找到菱形呢?又得到了以下的问题.
问题2:在问题1的条件下,能否得到菱形EFGH?
如图3,要找到E点并不困难,只需延长AC到K,使CK=BD,连接BK,过C作CE∥BK,交AB于E,再利用问题1的作法,可得四边形EFGH为菱形.
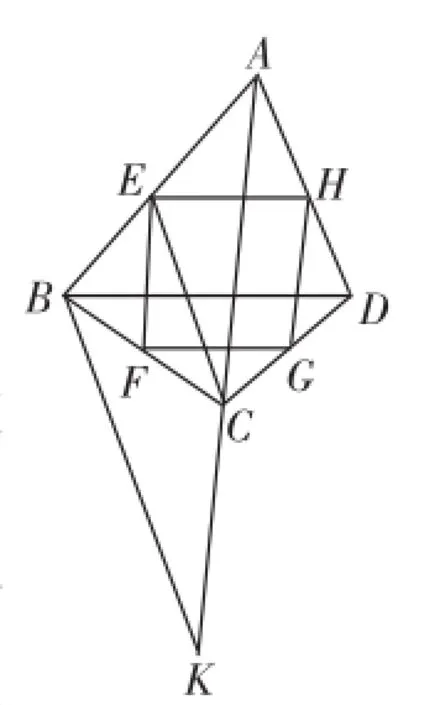
图3
这样已经弱化了中点的条件,但四边形EFGH的边与四边形ABCD的对角线仍是平行的,能否继续弱化使之成为一个新问题?
问题3:在四边形ABCD的边上能否找到点E、F、G、H,使它们不是各边中点,且与AC、BD不平行,但四边形EFGH却是平行四边形?
如图4,在AB、BC上分别取点E、F,以FE、FC为邻边作平行四边形EFCK,过K作HK∥CD,过H作HG∥CK,连接FG、EH,四边形EFGH一定是平行四边形.
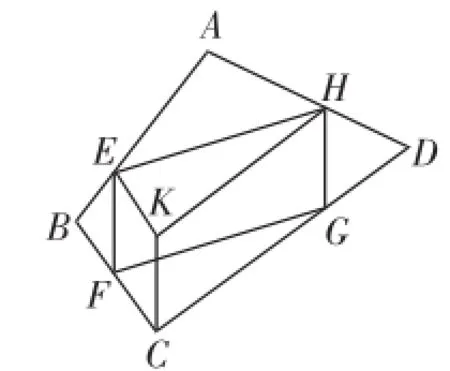
图4
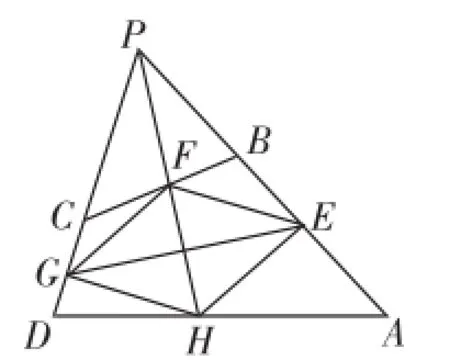
图5
问题4:按照问题3的要求,能否使所得到的四边形EFGH为菱形?
如果参照问题3的方法,通过计算EF、FG的长,由EF=FG,求E、F的位置,显然有很大困难.菱形的对角线的特性:菱形的对角线互相垂直平分,且平分一组对角,为解决问题4提供了思路.如图5,只要延长AB和DC,使它们交于点P,作∠APD的角平分线交BC、AD于F、H,作FH的垂直平分线,交AB于E,交CD于G,四边形EFGH就一定是一个菱形.
这里需要指出以下两点:一是E、G可能落在BA与DC的延长线上,我们不妨认为也是可以的;二是当AB∥CD时,点P无法得到,可通过延长BC、AD得到P.如AB∥CD且BC∥AD时,可过AC、BD的交点任意作两条互相垂直的直线得到菱形.
评析:对习题的条件进行变换是改编习题最基本的形式.它能将一个问题从多个角度或反向来研究,通过将条件弱化或增强转化为新问题,引导学生对数学问题进行引申、推广,促使学生积极思考,寻找解决问题的方法,加深学生对知识的系统理解,增强学生解题的应变能力,培养学生自主探究、合作学习的能力.
二、变结论
例2如图6,正三角形ABC中,D、E分别在BC、AC上,AE=CD.连接AD、BE交于点P,求证:∠APE=60°.
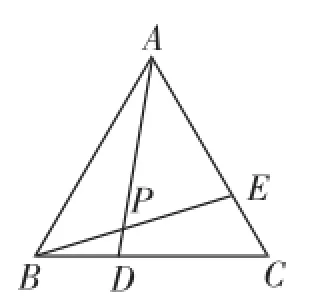
图6
本题是浙教版课标教材八年级上册“特殊三角形”目标与评定中一道经典老题,很多教师围绕图中的两对全等三角形做文章.仔细研究发现蕴含其中的六对相似三角形更是本题的亮点,笔者利用这一发现,设计如下试题.
如图6,正三角形ABC中,AB=6,D、E分别在BC、AC上,AE=CD.连接AD、BE交于点P.
(1)求证△ABE≌△CAD;
(2)若AE=CD=4,求EP的长;
(3)当点E从点A运动到点C时,试求点P经过的路径的长.
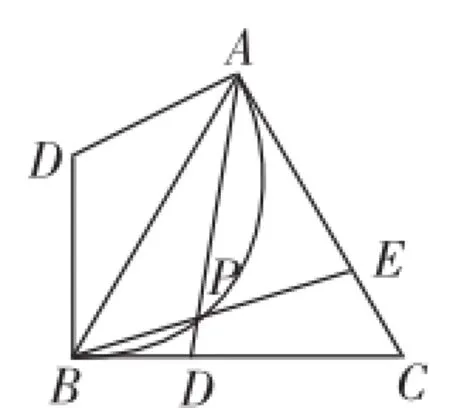
图7
整题短小精干,梯度明显,将全等、三线合一、勾股定理、方程、相似、圆等知识融合其中,尊重学生在学习数学方面的差异.第一问起点较低,却为后续探究作好了铺垫,第二问要求学生在熟悉情境中探寻陌生问题的解决方法,发现图中的两个三角形△APE和△BAE有公共角∠AEB,并且∠PAE=∠ABE,于是△APE∽△BAE,从而将求EP的长转化为求BE的长,利用三线合一和勾股定理,过点B作AC边上的高,不难求得BE=2,于是EP=此小题还可设问求AP的长.也可以连接DE,若∠AEB=∠CED,求AE的长.第三问将静态变为动态,思维能力继续提升,为一些优秀学生提供了展示自己的舞台.如图7,首先经过尝试画图不难发现点P的路径为一段圆弧,当E为AC的中点时,点P经过弧AB的中点,此时△ABP为等腰三角形,且∠ABP=∠BAP=30°,所以∠AOB=120°.因为AB=6,所以OA=2,点P的路径为
评析:通过对习题结论的改变,考查目标、设问视角相应发生改变,要求更全面地理解、分析、归纳各种关系,同时结合教学实际激发学生的探索欲,达到活跃思维、强化思想方法的掌握。
三、变背景
例3观察下列多项式,4a+b,8a+4b,12a+9b,16a+ 16b,…,则第n个多项式可表示为_______.
本题难度不大,但背景老套,缺乏鲜活感、层次感.在初三复习阶段笔者将其改成含三个层次,蕴含探寻规律、方程、函数等知识的试题.
观察下表:
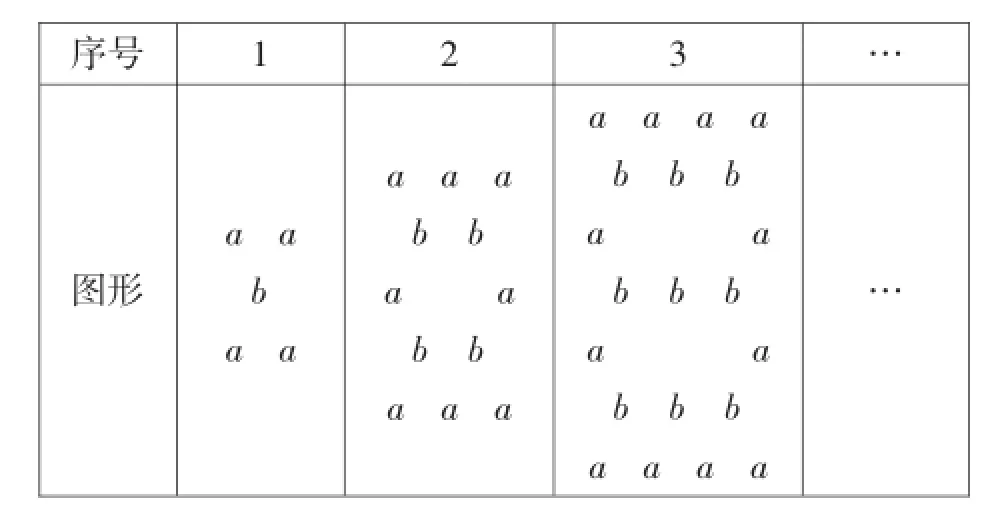
序号1 2 3…图形aa b aa aaa bb aa bb aaa aaaa bbb aa bbb aa bbb aaaa…
我们把某格中字母的和所得多项式称为“特征多项式”,例如,第1格的“特征多项式”,为4a+b.回答下列问题.
(1)第3格的“特征多项式”为______,第4格的“特征多项式”为_____,第n格的“特征多项式”为______.
(2)第1格的“特征多项式”的值为-10,第2格的“特征多项式”的值为-16,
①求a、b的值.
②在此条件下,第n格的“特征多项式”是否有最小值?若有,求出相应的n的值;若没有,请说明理由.
本题将代数式规律以表格型辅以新定义形式呈现,令人耳目一新,问题的设置起点低、梯度明显,有利于不同层次学生的发挥.彰显了新课标中“由知识立意向能力立意”过渡的要求,是坚持学生“可持续发展”理念的体现.
例4已知:如图8,最大正方形的面积等于较小两个正方形面积的和.求证:这三个正方形的边构成的△ABC是直角三角形.
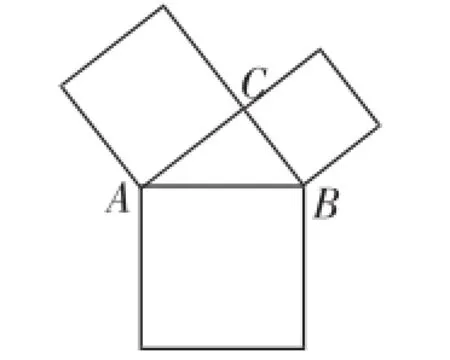
图8
本题是浙教版课标教材八年级上册“探索勾股定理”中判定直角三角形的一道试题.近年来,以勾股定理中“赵爽弦图”“勾股树”等为模型的试题层出不穷,但富有新意的却不多.笔者尝试设计了两题供读者赏析.
试题1:古印度有一种证明勾股定理的方法:如图9,过正方形ADEC的中心O,作两条互相垂直的直线,将它分成4份.如果这两条直线作得恰当,所分成的四部分和小正方形BCMN恰好能拼成大正方形ABPQ.这种方法,不用运算,单靠移动几块图形就直观地证明出了勾股定理,堪称“无字的证明”!若BC=6,AC=8,则EF为______.
试题2:如图10,是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成的.已知正方形ABCD的边长为4,5个等圆分别内切于直角三角形和正方形EFGH各边,则图中圆的半径是__________.
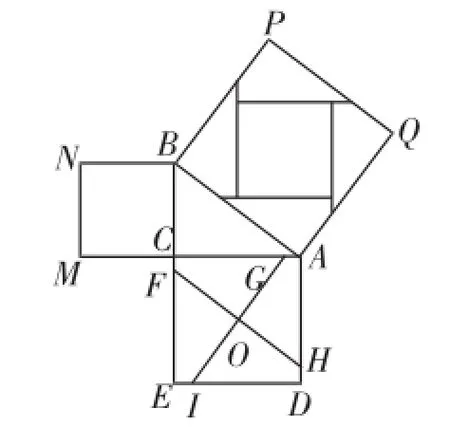
图9
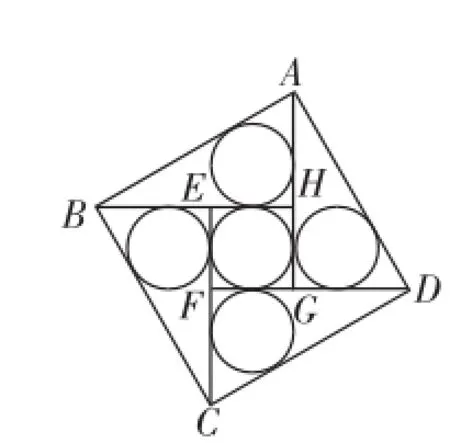
图10
评析:通过改变图形或情境等问题背景,能训练学生的理解能力和建模能力.操作时我们可选择一些具有代表性的习题,在同一种模型上换不同的实际背景,拓展其内涵.
事实上,对教材习题的微改编不仅能引领学生完善知识系统掌握的过程,改变学生单一的思维方式,使学生的想象力和创造力得到充分的开掘与发挥,更能促进教师的专业发展,改变教师的教学方式,使教师的命题更好地为课堂教学服务.
1.中华人民共和国教育部制定.义务教育数学课程标准(2011年版)[M].北京:北京师范大学出版社,2012.
2.朱林.能产生实效性的习题设计[J].中学数学教育,2011(9).
3.安国钗.推陈出新精彩纷呈——对一道作业题的开发、引申与挖掘[J].中学数学教育,2011(10).
4.范锦君.初中数学“四步骤”命题策略的实践与思考[J].中学数学(下),2014(10).Z
