Traffic flow sensitivity to visco-elasticityM.N.Smirnovaa,d,A.I.Bogdanovaa,Zuojin Zhua,b,∗,N.N.Smirnova,c

Fulty of Mehnis n Mthemtis，Mosow M.V.Lomonosov Stte University，Mosow 119992，RussiFulty of Engineering Siene，University of Siene n Tehnology of Chin，Hefei 230026，ChinSientifi Reserh Institute for System Anlysis of Russin Aemy of Sienes，Mosow 117218，RussiSint Petersurg Stte Polytehnil University，St.Petersurg 195251，Russi



Traffic flow sensitivity to visco-elasticity
M.N.Smirnovaa,d,A.I.Bogdanovaa,Zuojin Zhua,b,∗,N.N.Smirnova,c

aFaculty of Mechanics and Mathematics，Moscow M.V.Lomonosov State University，Moscow 119992，Russia
bFaculty of Engineering Science，University of Science and Technology of China，Hefei 230026，China
cScientific Research Institute for System Analysis of Russian Academy of Sciences，Moscow 117218，Russia
dSaint Petersburg State Polytechnical University，St.Petersburg 195251，Russia

H I G H L I G H T S

·Visco-elasticity effect on traffic flows.

·Self-organization is a crucial feature in traffic flow pattern formation.

·Optimization of traffic control regulations is necessary.

A R T I C L EI N F O

Article history：

in revised form

10 May 2016

Accepted 10 May 2016

Available online 1 June 2016

Viscoelastic modeling Self-organization

This letter reports traffic flow sensitivity to visco-elasticity,with the traffic flow modeling briefly described at first and then used to do traffic flow simulations whose results can reflect the properties of spatial-temporal evolution of ring traffic flow.It reveals that visco-elasticity plays crucial role in formation of traffic flow patterns,implying that self-organization of traffic flow is crucial in determining traffic flow status.

©2016 The Author（s）.Published by Elsevier Ltd on behalf of The Chinese Society of Theoretical and

Applied Mechanics.This is an open access article under the CC BY-NC-ND license（http://creativecommons.org/licenses/by-nc-nd/4.0/）.

Trafficflowshavebeenextensivelystudiedduetoitssignificant impacts on work and life in modern society.Many models have been developed to ascertain traffic flow characteristics and understandintrinsicpropertiesoftrafficwavepropagation,among which is vehicular mass conservation based Lighthill,Whitham, and Richards（LWR）model［1,2］,probably the simplest one being abletocapturesomecrucialflowfeaturesonhighways,andpredict traffic shock waves with relatively steep wave fronts［3］.Although results of LWR traffic modeling are not completely favorable for predicting traffic waves spreading on highways,its extensions can predict traffic hysteresis［4］,evolution of density waves［5］,and critical transition of bottleneck in traffic flows［6］.

In traffic modeling,further involving momentum conservation leads to the occurrence of high-order models,among which are the Euler model［7］,the gas-kinetic-based model［8,9］,the cluster effect model［10］,and the generic model［11-13］.High-order models can explain the vehicular stop and moving phenomena and predict traffic wave spreading successfully.Although a critic comment［14］has deeply suspected high-order models,there are still many remarkable applications［15-17］and further developments［18-28］.

In traffic systems,spatial-temporal pattern formations have a surprisingly rich spectrum,which can be described by the carfollowing models,the cellular automaton models［29-31］,the gaskinetic models,or the fluid-dynamical models［32］.Using methods in statistical physics and nonlinear dynamics to self-driven manyparticle systems,Helbing has answered some flow questions［33］.

As soon as instantaneous traffic flow rate q is not equal to equilibrium flow rate qe,time headway will automatically adjust to approach 1/qe［34］.By introducing traffic viscosity and pressure in some high-order models［10,35］,this self-organization of traffic flow has been considered.In congested traffic flows where traffic density is larger than saturation densityρs（=ρm/e）as shown in Fig.1,it is common to observe instantaneous variation of flow rate.The interaction of traffic flow waves is more intensive,causing the occurrence of a synchronized flow regime or a jam existing regime［36］.However,the flow is homogeneous and stable for the denser traffic flow where traffic density is larger than the second critical densityρc2［37］.

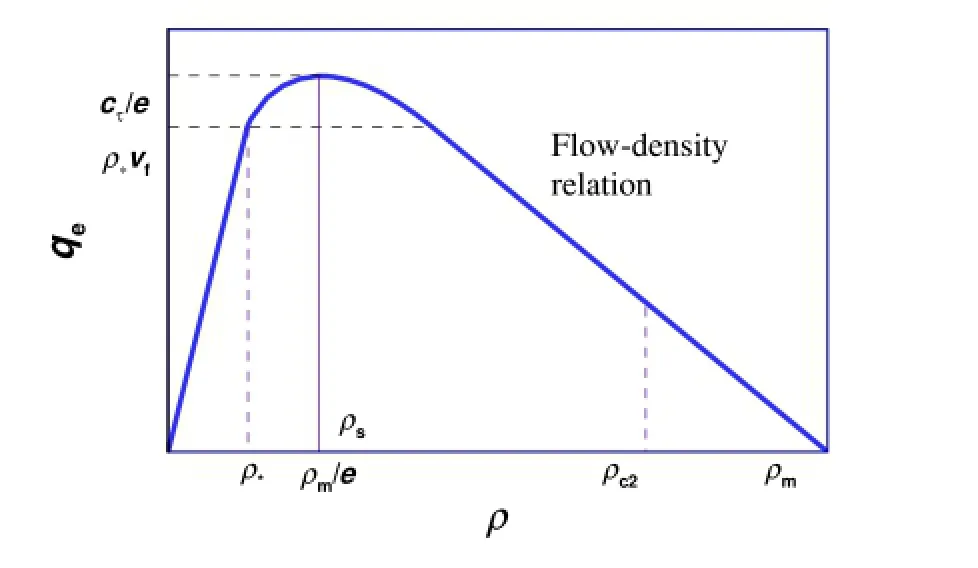
Fig.1.Fundamental diagram used in Ref.［21］.

Since relaxation and elastic processes are intrinsically related from points of view in fluid mechanics,relaxation time has been usedfordenotingexternalforceoftrafficflows,visco-elastictraffic flow models have some grounds of fluid mechanics.For simplicity, we assume:（1）ramp flow effect is negligible；（2）road capacity is insensitive to vehicular drivers；（3）traffic flow satisfies linear viscoelastic constitutive relation.The main reason for the 3rd assumption has been reported in Ref.［22］.

Let qebe traffic flow rate under equilibrium flow state,using traffic fundamental diagram as shown in Fig.1,it has the form

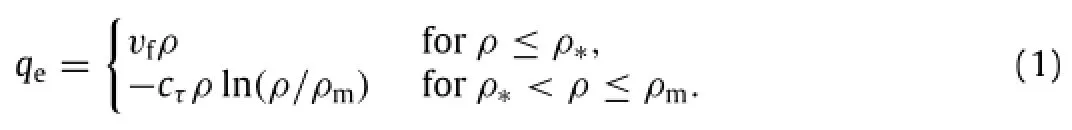
As reported previously［27］,traffic pressure p is proportional to density,withtheproportionalcoefficientbeingthesquareoftraffic sound speed c2.Using jam density and jam pressure of traffic flow, p has the form

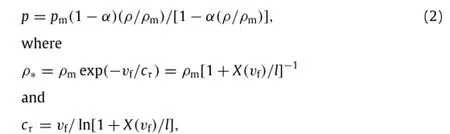
as shown in Fig.1.Note thatα=lρm,l is average vehicular length, X（vf）is braking distance depending merely on free-flow speedvf. The fundamental diagram is driver-dependent［23］.Clearly,it has significant impact on traffic road operation［38］.While the jam pressure is

where

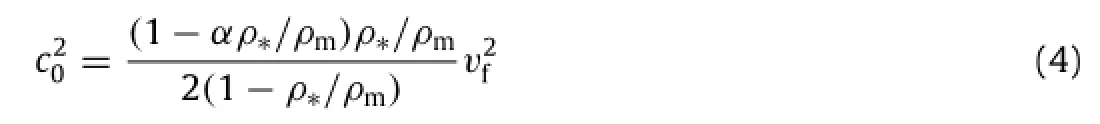
with the sound speed in traffic flows given by

As expressed by Eq.（5）,traffic sound speed is proportional to free flow speedvf.To express relaxation timeτexplicitly,supposing（c·τ）=const,and denoting traffic jam relaxation time byτ0= l0/cτwith traffic length scale l0,we have［27］

Table 1　Traffic operation parameters on the ring road.

Obviously,the relaxation timeτdecreases linearly with traffic density,implying that equilibrium flow state can play a more important role under congested flow conditions,as external traffic force is explicitlyτ-dependent.

Therefore,the governing equations of viscoelastic traffic flows are（see also in Ref.［27］）

with R satisfying the expression

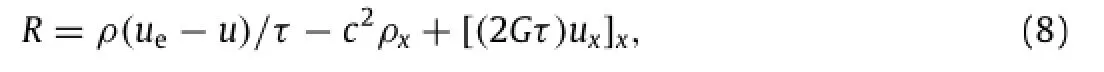
where x is space coordinate,G is the modulus of traffic flow elasticity,2Gτ= ρν,withνdenoting the kinematic viscosity of trafficflow.Theinclusionofelasticityallowstheaccelerationspeed varyingwithviscoelasticdependentforce,implyingthetrafficflow model has intimately involved the influences of neighborhood traffic operations.

To verify the proposed model briefly described above,numericaltestsarecarriedouttoshowthevisco-elasticeffectonringroad traffic flows.The road length is assumed to be 860l0,with a length unit l0=160 m,and a velocity scale given byv0=vfρ∗/ρm≈3.176 m·s-1,and time scale t0=l0/v0≈50.377 s.The initial density condition is given by

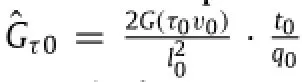
The comparison of ring traffic patterns is illustrated in Fig.2（a-c）,where the ring traffic density contours are shown in flood-typeformandlabeledbyvaluesof0.309,0.35,0.618,and0.7, respectively.This means the density in the blue region is below 0.309,in the red region is larger than 0.7.While traffic density in the cyan region has a value in the range of［0.309，0.35］,with the green and yellow regions being relevant to the density range［0.35，0.618］,and［0.618，0.7］,respectively.FromFig.2（a-c）,itcan be seen that with the increase of viscoelastic parameterγ,selforganization of traffic flows increases.Since the flow pattern has become more regular as a result of interaction of traffic shock and deflation waves,it reveals that self-organization can impact traffic flow pattern formation significantly.

To illustrate traffic sensitivity to visco-elasticity,distributions of time-average based mean density and speed are given in Fig.3（a-b）,where green-solid,blue-dash,and dash-dot black curves are relevant toγ=0.03125,0.0625,and 0.125,respectively.The mean traffic density and speed on the ring road are both clearly sensitive to parameterγ,a smallerγvalue can lead to a larger variation range of traffic density and speed.As seen inFig.2（a-c）,self-organizationrepresentedbyγ,canbringaboutsignificantly difference of traffic wave structures.The traffic wave interaction has resulted in oscillated distributions of mean density and speed,with the oscillation mode beingγ-dependent.

Fig.2.（Color on online）Comparison of ring traffic density contours in the t-x/l0plane,（a）γ=0.03125,（b）γ=0.0625,and（c）γ=0.125.（For interpretation of the references to color in this figure legend,the reader is referred to the web version of this article.）

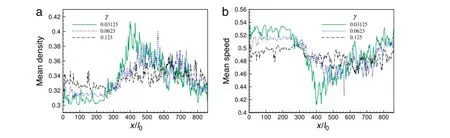
Fig.3.Distributions of（a）mean density and（b）mean speed on the ring road.（For interpretation of the references to color in this figure legend,the reader is referred to the web version of this article.）

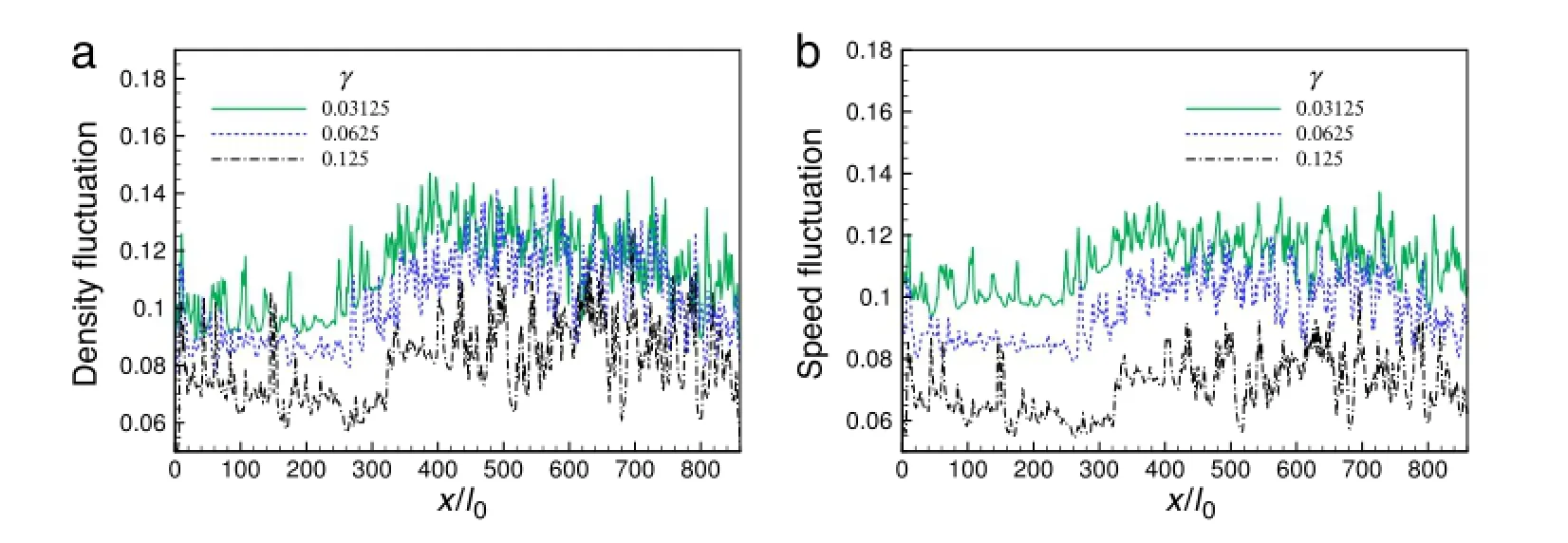
Fig.4.Distributions of（a）density and（b）speed fluctuations on the ring road.

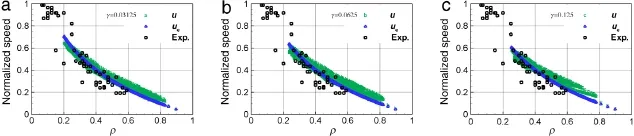
Fig.5.Comparison of traffic speed with existing measured data at x/l0=430,（a）γ=0.03125,（b）γ=0.0625,and（c）γ=0.125.The observation data are obtained from Ref.［39］,and the jam density for normalization is supposed to be 200 veh·mile-1.

The distributions of density and speed fluctuations are shown in Fig.4（a-b）,where the so-called fluctuation is just time-average based root mean square（RMS）value of some variable.Totally, the smaller the value of visco-elastic parameterγ,the larger RMS values are for traffic density and speed.Since the distributions intrinsically depend on the traffic wave propagation on the ring road,at a given spatial point,theγinduced difference of RMS values of density and speed has some uncertainty.

As shown in Fig.5（a-c）,the instantaneous speed u recorded at the section of x=430 plotted as a function of density is labeled by green alphabets a,b,and c,respectively.The instantaneous equilibrium speed ueat the section of x=430 determined by fundamental diagram Eq.（1）is labeled by non-filled blue triangles,with existing measured data［39］labeled by non-filled black squares.The comparison of speed-density relation at a given observing road section with measured data,not only shows the traffic sensitivity to visco-elasticityγ,but also reflects to someextent the potential of viscoelastic traffic flow model,and the reliability of simulation results.

The viscoelastic traffic model introduced above has potential in traffic flow simulations.Numerical tests revealed that viscoelastic sensitivity of traffic flows is certainly larger,indicating that selforganizing traffic flows play a significant role in flow pattern formation,and it is crucial in determining traffic flow status. This suggests that optimization of traffic control regulations is necessary in reality as traffic flow has become a key feature of modern society.

Acknowledgments

Here we acknowledge the support of Russian Foundation for Basic Research（RFBR 13-01-12056）and the National Natural Science Foundation of China（10972212）.

［1］M.J.Lighthill,G.B.Whitham,On kinematic waves:ii.a theory of traffic flow on long crowded roads,Proc.R.Soc.Lond.Ser.A math.Phys.Eng.Sci.229（1955）317-345.

［2］P.I.Richards,Shock waves on the freeway,Oper.Res.4（1956）42-51.

［3］R.D.Kuhne,P.Michalopoulos,Continuumflowmodels,in:TrafficFlowTheory: A State of the Art Report Revised Monograph on Traffic Flow Theory,1997.

［4］G.C.K.Wong,S.C.Wong,A multi-class traffic flow model-an extension of LWR model with heterogeneous drivers,Transp.Res.A 36（2002）827-841.

［5］Z.J.Zhu,T.Q.Wu,Two-phasefluidsmodelforfreewaytrafficanditsapplication to simulate the evolution of solitons in traffic,ASCE,J.Transp.Eng.129（2003）51-56.

［6］G.L.Chang,Z.J.Zhu,A macroscopic traffic model for highway work zones: formulations and numerical results,J.Adv.Transp.40（2006）265-287.

［7］H.J.Payne,Models of freeway traffic and control,Simul.Counc.Proc.1（1971）51-61.

［8］D.Helbing,M.Treiber,Gas-kinetic-based traffic model explaining observed hysteretic phase transition,Phys.Rev.Lett.81（1998）3042-3045.

［9］S.P.Hoogendoorn,P.H.L.Bovy,Continuum modeling of multiclass traffic flow, Transp.Res.B 34（2000）123-146.

［10］B.S.Kerner,P.Konhäuser,Cluster effect in initially homogeneous traffic flow, Phys.Rev.E 48（1993）2335-2338.

［11］J.P.Lebacque,S.Mammar,H.Haj-Salem,Generic second order traffic flow modelling,in:R.E.Allsop,G.H.Benjiamin（Eds.）,Transportation and Traffic Theory,Elsevier,Oxford,2007,pp.755-776.

［12］P.Zhang,S.C.Wong,S.Q.Dai,Aconservedhigherorderaniso-tropictrafficflow model:description of equilibrium and non-equilibrium flows,Transp.Res.B 43（2009）562-574.

［13］J.P.Lebacque,M.M.Khoshyaran,A variational formulation for higher order macroscopic traffic flow models of the gsom family,Transp.Res.B 57（2013）245-265.

［14］C.Daganzo,Requiem for second-order fluid approximations of traffic flow, Transp.Res.B 29（1995）277-286.

［15］W.L.Jin,H.M.Zhang,The formation and structure of vehicle clusters in the payne-whitham traffic flow model,Transp.Res.B 37（2003）207-223.

［16］P.Zhang,S.C.Wong,Essence of conservation forms in the travelling wave solutions of higher-order traffic flow models,Phys.Rev.E 74（2006）026109.

［17］Z.H.Ou,S.Q.Dai,P.Zhang,et al.,Nonlinear analysis in the Aw-Rascle anticipation model of traffic flow,SIAM J.Appl.Math.67（2006）605-618.

［18］A.Klar,R.Wegener,Kinetic derivation of macroscopic anticipation models for vehicular traffic,SIAM J.Appl.Math.60（2000）1749-1766.

［19］A.Aw,M.Rascle,Resurrection of second order models of traffic flow,SIAM J. Appl.Math.60（2000）916-938.

［20］H.M.Zhang,Driver memory,traffic viscosity and a viscous vehicular traffic flow model,Transp.Res.B 37（2003）27-41.

［21］A.B.Kiselev,V.F.Nikitin,N.N.Smirnov,et al.,Irregular traffic flow on a ring road,J.Appl.Math.Mech.64（2000）627-634.

［22］Z.J.Zhu,C.Yang,Visco-elastic traffic flow model,J.Adv.Transp.47（2013）635-649.

［23］G.Costeseque,J.P.Lebacque,A variational formulation for higher order macroscopic traffic flow models:numerical investigation,Transp.Res.B 70（2014）112-133.

［24］A.Spiliopoulou,M.Kontorinaki,M.Papageorgiou,et al.,Macroscopic traffic flow model validation at congested freeway off-ramp areas,Transp.Res.C 41（2014）18-29.

［25］A.I.Delis,I.K.Nikolos,M.Papageorgiou,High-resolution numerical relaxation approximations to second-order macroscopic traffic flow models,Transp.Res. C 44（2014）318-349.

［26］M.N.Smirnova,A.I.Bogdanova,Z.J.Zhu,etal.,Mathematicalmodelingoftraffic flows using continuum approach:visco-elastic effect in traffic flows,Math. Model.26（2014）54-64（in Russian）.

［27］A.I.Bogdanova,M.N.Smirnova,Z.J.Zhu,et al.,Exploring peculiarities of traffic flows with a viscoelastic model,Transp.A:Transp.Sci.11（2015）561-578.

［28］S.P.Hoogendoorn,F.van Wageningen-Kessels,W.Daamen,et al.,Continuum theory for pedestrian traffic flow:local route choice modelling and its implications,Transp.Res.C 59（2015）183-197.

［29］K.Nagel,M.Schreckenberg,A cellular automaton model for freeway traffic, J.De Phys.I 2（1992）2221-2229.

［30］D.Helbing,B.A.Huberman,Coherent moving states in highway traffic,Nature 396（1998）738-740.

［31］D.Chowdhury,L.Santen,A.Schadsschneider,Statistical physics of vehicular traffic and some related systems,Phys.Rep.329（2000）199-329.

［32］T.Nagatani,Thephysicsoftrafficjams,Rep.Progr.Phys.65（2002）1331-1386.

［33］D.Helbing,Trafficandrelatedself-drivenmany-particlesystems,Rev.Modern Phys.73（2001）1067-1141.

［34］J.M.Del Calstillo,Propagation of perturbations in dense traffic flow:a model and its implications,Transp.Res.B 35（2001）367-389.

［35］M.Hilliges,W.Weidlich,A phenomenological model for dynamic traffic flow in networks,Transp.Res.B 29（1995）407-431.

［36］B.S.Kerner,Synchronized flow as a new traffic phase and related problems for traffic flow modelling,Math.Comput.Modelling 35（2002）481-508.

［37］M.Schönhof,D.Helbing,Criticism of three-phase traffic theory,Transp.Res.B 43（2009）784-797.

［38］F.A.Haight,Mathematical Theories of Traffic Flow,Academic Press,New York, 1963.

［39］W.R.McShane,R.P.Roess,E.S.Prassas,Traffic Engineering,second ed., Prentice-Hall,New Jersey,1998,pp.282-306.

6 May 2016

at:Faculty of Engineering Science,University of Science and Technology of China,Hefei 230026,China.Fax:+86 551 63631760.

E-mail address：zuojin@ustc.edu.cn（Z.Zhu）.

URL：http://new.math.msu.su/department/volnogaz/photos/smirnov.html

（N.N.Smirnov）.

http://dx.doi.org/10.1016/j.taml.2016.05.003

2095-0349/©2016 The Author（s）.Published by Elsevier Ltd on behalf of The Chinese Society of Theoretical and Applied Mechanics.This is an open access article under the CC BY-NC-ND license（http://creativecommons.org/licenses/by-nc-nd/4.0/）.

*This article belongs to the Fluid Mechanics

Traffic flow sensitivity

Flow pattern formation