Visualizing surface strain distribution of facial skin using stereovisionNagisa Miura,Tsubasa Sakamoto,Yuichi Aoyagi,Satoru Yoneyama∗

Department of Mechanical Engineering，Aoyama Gakuin University，5-10-1 Fuchinobe，Sagamihara，Kanagawa 252-5258，Japan



Letter

Visualizing surface strain distribution of facial skin using stereovision
Nagisa Miura,Tsubasa Sakamoto,Yuichi Aoyagi,Satoru Yoneyama∗

Department of Mechanical Engineering，Aoyama Gakuin University，5-10-1 Fuchinobe，Sagamihara，Kanagawa 252-5258，Japan

H I G H L I G H T S

·Complicated shape of human’s face is measured by stereovision.

·Facial displacements and strains can be obtained.

·Strain concentrations are visualized by a developed measurement system.

A R T I C L EI N F O

Article history：

in revised form

25 January 2016

Accepted 26 May 2016

Available online 2 June 2016

Strain

Skin

Face

Wrinkle

Stereovision

Digital image correlation

An experimental technique has been developed for measuring and visualizing strain distribution on facial skin.A stereovision technique based on digital image correlation is employed for obtaining the displacement distribution on the human face.Time-variation of the movement of the facial skin surface is obtained from consecutive images obtained using a pair of high-speed cameras.The strains on the facial skin surface are then obtained from the measured displacements.The performance of the developed system is demonstrated by applying it to the measurement of the strain on facial skin during the production of sound.Results show that the strains on facial skin can be visualized.Further discussion on the relationship between the creation of wrinkles and strains is possible with the help of the developed system.

©2016 The Author（s）.Published by Elsevier Ltd on behalf of The Chinese Society of Theoretical and

Applied Mechanics.This is an open access article under the CC BY-NC-ND license（http://

creativecommons.org/licenses/by-nc-nd/4.0/）.

Human skin is influenced by various factors such as ultraviolet rays,stress,and aging.For example,wrinkles appear around the corner of the eye and the middle of the forehead with aging.The region where wrinkles appear is subjected to repeated deformation by daily motion,for example,the motion of blinking. It may be considered that the strains caused by such daily motions are closely related to the generation of wrinkles with aging. Therefore,it is necessary to measure the strain distribution on the skin surface where a wrinkle is generated.However,because the skin is very soft,and the skin surface has a complex threedimensional shape,it is not easy to measure the strains on skin.

There are various techniques for measuring strains［1,2］.Strain gauges can be used for measuring strains on skin［3］,however,a strain gauge method is not considered appropriate for measuring strains on skin because the rigidity of a strain gauge is usually higher than that of skin.In addition,strain distributions cannot be obtained when a strain gauge is used.Optical methods such as a two-dimensional digital image correlation method have also been used for measuring strain fields on human skin［4-6］.Among the strain measurement methods,stereovision［7,8］is one of the most suitablemethodsformeasuringstrainsonfacialskinbecauseitcan be used for measuring large strains on three-dimensional surfaces.

In the present study,an experimental technique for measuring and visualizing strain distribution on facial skin is developed. A stereovision technique based on digital image correlation is employed for obtaining the displacement distribution on the human face.Time-variation of the movement of the facial skin surface is obtained from consecutive images obtained using a pair of high-speed cameras.The strains on the facial skin surface are then obtained from the measured displacements by differentiating the displacements along the surface.The performanceofthedeveloped system isdemonstrated byapplying it to the measurement of the strains on facial skin during the production of sound.Results show that the strains on facial skin can be visualized.Further discussion on the relationship between the creation of wrinkles and strains is possible with the help of the developed system.

http://dx.doi.org/10.1016/j.taml.2016.05.005

Fig.1.Random pattern on skin surface created by a makeup airbrush.

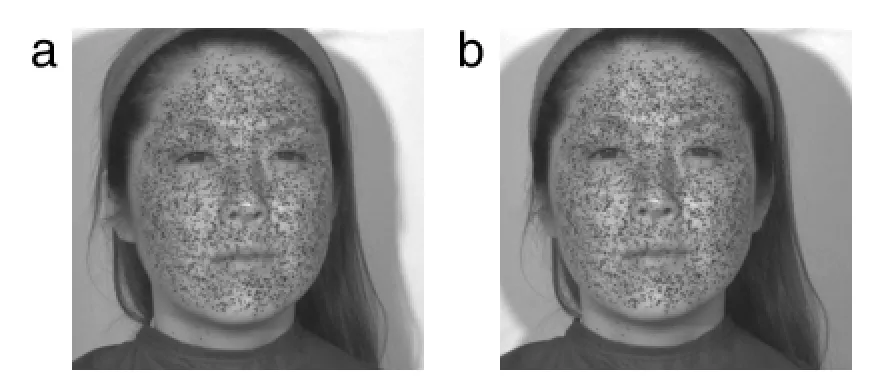
Fig.2.Example of stereo pair images:（a）left camera；（b）right camera.

Fig.3.Three-dimensional shape of the facial skin surface obtained by stereovision.

2095-0349/©2016 The Author（s）.Published by Elsevier Ltd on behalf of The Chinese Society of Theoretical and Applied Mechanics.This is an open access article under the CC BY-NC-ND license（http://creativecommons.org/licenses/by-nc-nd/4.0/）.

First,cameracalibrationisperformedtodeterminetheintrinsic and extrinsic parameters of the two cameras.Here,Zhang’s camera calibration method［9］is used.Next,measurement of the displacement on the face is performed.In order to obtain good correlation among images,a random pattern is created on the surface of the face using a makeup airbrush.Figure 1 shows an example of the random pattern on the skin surface.It is known that the size of the random pattern should be selected to oversampletheintensitypatternusingseveralsensorsforaccurate measurement.In this study,each random pattern is oversampled by 10-40 pixels.Then,the face is illuminated by multiple light sources.The face images are recorded using two high-speed cameras（1024×992pixels×8bits）ataframerateof100fps.Using a digital image correlation technique,the corresponding points between the stereo pairs of images are determined.Then,the three-dimensionalcoordinatesofthesurfaceofthefacebeforeand after deformation are obtained.The displacements are obtained by subtracting the coordinates before deformation from those after deformation.The subset size used for calculating the correlation is 31×31 pixels and the number of points where the displacement is determined is approximately 12000.

Figure2showsasetofstereoimagesofthehumanfaceobtained usingthetwocameras.Therandompatterncreatedbytheairbrush is observed.In addition,the difference of perspective due to the difference in the direction of viewing between the two cameras is recognized.Applying the digital image correlation technique［7,8］to the stereo pair images,the corresponding points between the images are identified.Here,the regions that are not observed from both cameras,such as the side of the nose,are excluded from the results.Then,the three-dimensional coordinates are determined based on the principle of stereovision.The shape of the face obtained by the stereo technique is shown in Fig.3.Parts such as eyes,nose,and cheek are recognized.That is,the threedimensional coordinates of the complex object can be obtained by stereovision.TheshapeinFig.3isusedasthereferencecoordinates for measuring the displacement and the strain.

Figure 4 shows examples of the image obtained by the left camera during the production of sound of‘AIUEO’.In these images,Fig.4（a）-（e）corresponds to the instant of the production of the sound‘A’,‘I’,‘U’,‘E’,and‘O’,respectively.The displacement distributions,ux,uy,and uz,are obtained from the images using the procedure described above,as shown in Fig.5.The contours in Fig.5 are the displacements at the instant of the production of sound‘A’.That is,the displacements in Fig.5 are obtained from the image shown in Fig.4（a）.By using this procedure,the variation in the displacements during the production of sound is obtained.

For calculating strains on a three-dimensional surface,the displacements should be differentiated along the tangential direction of the surface.Therefore,unlike the two-dimensional case,the derivatives of the surface displacements are not directly obtained because the direction of differentiation does not coincide with the coordinate system.In the present study,a simple method for obtaining strain distributions from measured displacements on a three-dimensional surface［10］is used.It is considered that the three-dimensional position of a point（x，y，z）and the surface displacements,ux（x，y，z）,uy（x，y，z）,and uz（x，y，z）,of an object surface are obtained experimentally at discretely sampled points on the Cartesian coordinate system.Figure 6 shows the schematic diagram of a part of a three-dimensional surface.Strain components at a point are determined from displacements at multiple points within the local area in Fig.6.It is noted that the shape of the local area in Fig.6 is a circle,but it can be of other shapessuchasasquare.Inordertodifferentiatethedisplacements, the displacement components within the local area should be transformed into displacements on a local Cartesian coordinate system whose axes coincide with the tangential directions of the surface.The local area on the three-dimensional surface in Fig.6 can be considered as a two-dimensional plane when the local area is small.Thus,the two-dimensional plane of the local area is expressed as

Fig.4.（a）-（e）images during the production of sound obtained by the left camera.

Fig.5.An example set of the displacement distributions at the instant of the production of‘A’:（a）ux；（b）uy；（c）uz.

Fig.6.Local area and unit vectors on three-dimensional surface.

where a,b,and c are the coefficients that can be determined by the method of least-squares.The unit normal vector n of the fitted plane is obtained as

where n1,n2,and n3are the components of the vector n.The unit tangential vectors t1and t2of the surface are

Therein,t11,t12,and t13,and t21,t22,and t23are the components of the vectors t1and t2,respectively.The vectors t1and t2lie on the fitted plane.The symbol j represents the unit vector of the y direction.Therefore,the unit vector t1is perpendicular to the y axis.Usingthevectorst1,t2,andn,thepositionx,y,andz ofapoint onthethree-dimensionalsurfaceandthedisplacementsux,uy,and uzcan then be expressed on the local coordinate system x′，y′，z′as

where t1,t2,and n are the first,second,and third rows of the rotation matrix.The local coordinate system lies on the x′-y′plane.Therefore,the displacements u′xand u′ycan be treated as the in-plane displacement components in the local coordinate system.After the coordinate transform,the differentiation of the displacements can be performed utilizing the method of leastsquares,and the strain distributions are obtained.

The principal strains,ε1andε2,are evaluated during the production of sound,as shown in Fig.7.The maximum principal strainsε1in Fig.7（a）-（e）and the minimum principal strainsε2in Fig.7（f）-（j）correspond to the image in Fig.4（a）-（e）.The strain concentration is observed at the corner of the mouth and around the chin.On the other hand,different from the strains during blinking［10］,the striped strain distribution on the cheek is not observed.

Fig.7.Variations in principal strains during production of sound corresponding to Fig.4:（a）-（e）ε1；（f）-（j）ε2.

Fig.8.Variations in strains:（a）images；（b）ε1；（c）ε2；（c）θ.

Another example of strain measurement is shown below.The facial strains during blinking are analyzed by the aforementioned procedure.Figure 8 shows the time-variation of the image observed from the left camera,the principal strainsε1andε2,and theprincipaldirectionθaroundtheeyeduringtheblink.Here,only the image size of 320×300 pixels region that is cropped from the image of 1024×992 pixels is shown in Fig.8（a）to protect the humansubject’sprivacy.Asshowninthisfigure,thestrainsaround the eye vary with time.The strain concentration is observed at the early stage of the blink.In addition,it is observed in Fig.8（d）that thestrainsinthehorizontaldirectionaredominantatthecornerof theeyeatthisstage.Atthelatterstage,ontheotherhand,thestrain concentrationdecreasesandtheprincipaldirectionatthecornerof the eye changes to the vertical direction.Further discussion on the relationship between strains and wrinkles that appear with aging is discussed in another paper.

As shown by these results,strains on the face can be visualized by the developed system.It is expected that the developed system canbeusedforfurtherdiscussiononthemechanismofthecreation of wrinkles with aging.

Anexperimentaltechniqueformeasuringandvisualizingstrain distribution on facial skin has been described.A stereovision technique based on digital image correlation was employed for obtaining the displacement distribution on the human face. Results show that strains on facial skin can be visualized.Further discussion on the relationship between the creation of wrinkles and strains is possible with the help of the developed system.

Acknowledgment

The authors appreciate the financial support received from the Skincare Research Laboratory of Kanebo Cosmetics Inc.

［1］J.W.Dally,W.F.Riley,Experimental Stress Analysis,third ed.,McGraw-Hill, New York,1991.

［2］P.K.Rastogi,Photomechanics,Springer,Berlin,1999.

［3］Y.Nishio,Y.Ito,Y.Kagiyama,et al.,Proposal of mechanical prophylaxis of pressure ulcers to arise at face during spinal surgery-approach in strain measurement method of skin with strain gauge,in:Proc.of 47th Symposium on Stress-strain Measurement and Strength Evaluation,Japanese Society for Non-Destructive Inspection,2016,pp.29-34.

［4］H.Marcellier,P.Vescovo,D.Varchon,et al.,Optical analysis of displacement and strain fields on human skin,Skin Res.Technol.7（2001）246-253.

［5］I.A.Staloff,E.Guan,S.Katz,et al.,An in vivo study of the mechanical properties of facial skin and influence of aging using digital image speckle correlation, Skin Res.Technol.14（2008）127-134.

［6］I.A.Staloff,M.Rafailovitch,Measurement of skin stretch using digital image speckle correlation,Skin Res.Technol.14（2008）298-303.

［7］J.-J.Orteu,3-D computer vision in experimental mechanics,Opt.Lasers Eng. 47（2009）282-291.

［8］M.A.Sutton,J.-J.Orteu,H.W.Schreier,Image correlation for shape,in:Motion and Deformation Measurements,Springer,New York,2009.

［9］Z.Zhang,A flexible new technique for camera calibration,IEEE Trans.Pattern Anal.Mach.Intell.22（2000）1330-1334.

［10］S.Yoneyama,Computing strain distributions from measured displacements on a three-dimensional surface,J.JSEM 10（2010）113-118.

12 November 2015

.

E-mail address：yoneyama@me.aoyama.ac.jp（S.Yoneyama）.