BDS卫星精密星历中不同类型轨道的插值分析
2016-09-19李晓光程鹏飞成英燕
李晓光,程鹏飞,成英燕
(1.辽宁工程技术大学,辽宁 阜新 123000;2.中国测绘科学研究院,北京 100830)
BDS卫星精密星历中不同类型轨道的插值分析
李晓光1,2,程鹏飞2,成英燕2
(1.辽宁工程技术大学,辽宁 阜新123000;2.中国测绘科学研究院,北京100830)
为了进一步研究使用精密星历获取BDS卫星精确的、更高采样率的轨道位置的问题,提出应用拉格朗日和牛顿插值对3类BDS卫星轨道进行内插的方法,分析了2种内插对3类卫星的适用性。结果表明,要想得到最佳收敛效果应用的收敛阶数是不同的,GEO最佳收敛在6~7阶,IGSO最佳收敛在8~10阶,MEO最佳收敛在10~11阶。
BDS;精密星历;拉格朗日插值;牛顿插值;GEO
0 引言
在北斗卫星导航系统(BeiDou navigation satellite system,BDS)精密星历的应用中,正确获取BDS卫星精确的轨道位置是需要解决的基础问题。卫星精密星历采用sp3格式,其存储方式为ASCII文本文件,内容包括表头信息以及文件体[1-2],文件体中每隔15 min给出一个卫星的位置[3],有时还给出卫星的速度和钟差,主要提供卫星精确的轨道位置。而BDS接收机的采样率一般为30 s或者15 s,甚至更密;因此要想利用某一时刻的卫星位置,就必须对精密星历进行高精度的插值。
本文利用武汉大学发布的2015年第74天广播星历采用拉格朗日和牛顿插值方法进行插值,并进行比较分析。
1 Lagrange插值方法原理


L1(xk)=yk,L1(xk+1)=yk+1。
(1)
则其线形插值多项式为
L1(x)=yklk(x)+yk+1lk+1(x)。
(2)
其中

式(2)称为Lagrange线形插值基函数。
同理,相应的Lagrange插值多项式为

(3)
其中

式(3)是n次插值基函数,满足条件
(4)
对于n阶插值,即有n+1个已知点,是内插位于这n+1个点之间的任意位置的函数值。
拉格朗日多项式插值模型简单,是经典的插值算法;但当精度不够而需要增加新的插值节点时,原来的插值多项式包括连续乘积项都不能使用,必须重新构造1个插值多项式。
2 Newton插值方法原理
Newton插值将插值基函数[4]定义为

(5)
其多项式的系数是各阶均差,定义为:
1)1阶均差

(6)
2)2阶均差
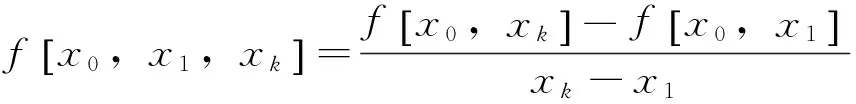
(7)
3)k阶均差
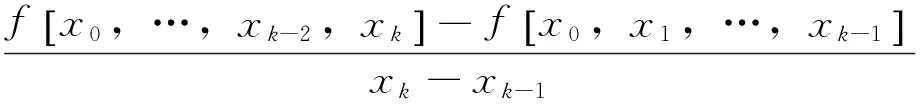
(8)
根据均差定义,高阶均差是低1阶均差的均差,因此可以用表 1 中递推关系来计算各阶均差。
4)Newton均差插值多项式


(9)
从上述定义可以看出:基函数的系数就是表1中主对角线元素,于是在实际计算中,可以先将表1列出。当增加节点时,只需在表的最下面增加1行,右面增加1列高阶均差即可,原来计算全部有效。这样就避免了增减节点引起插值基函数的改变,导致整个公式的变化。

表1 Newton各阶均差表
3 BDS精密星历内插
本文采用2015年第74天 05∶00∶00至10∶00∶00的3类卫星的精密星历,运用MATLAB[5]对07∶30∶00时刻卫星轨道进行2种方法的插值,并对原精密星历数据进行对比。
1)GEO卫星。BDS在轨工作卫星有5颗地球静止轨道(geostationary Earth orbit,GEO)卫星[6](如表2所示)。选取C01号卫星为案例进行插值分析。由于GEO卫星是静止轨道卫星,因此这类卫星坐标基本不变[7];但在3个方向也会呈现周期变化如图1~图3,取7 d的精密星历坐标画出。

表2 C01卫星插值结果 mm

图1 X方向坐标变化

图2 Y方向坐标变化
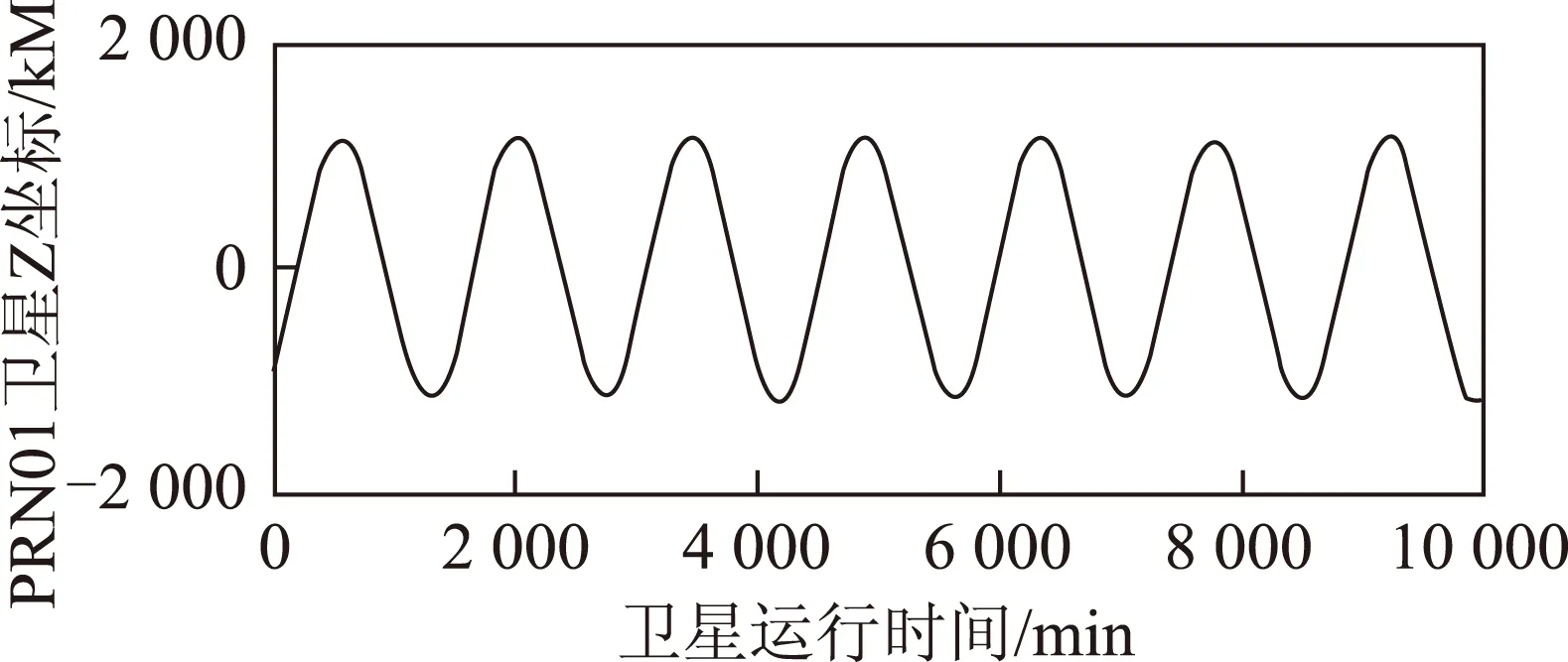
图3 Z方向坐标变化
由图1~图3可以看出GEO卫星在X、Y方向上的变化存在1 d和0.5 d周期项,在Z方向上存在1 d周期项,对于它的周期变化可能是由卫星机动[8]、太阳光压等因素造成的。
对于低阶插值,2种方法都能够迅速收敛。对于X、Z方向上的残差,在6阶插值时达到最低的mm级,阶数大于6以后,用增加阶数的方法提高精度不显著,存在震荡现象;Y方向上7阶达到最低的mm级。在效率方面,由于只解算1组数据,耗时都很少,但Newton插值方法要比Lagrange插值方法快2/10。对于大数据解算来说,会产生较大时间差。
对于其他GEO卫星进行插值都能迅速收敛,最佳收敛阶数大多分布在6~7阶。
2)IGSO卫星。BDS在轨工作卫星有5 颗倾斜地球同步轨道(inclined geo-synchronous orbits,IGSO)卫星[6]。选取C06号卫星为案例进行插值分析,如表3所示。
对于IGSO卫星,2种插值也能迅速收敛,但较GEO卫星来说相对慢些:Y、Z坐标方向上在8阶插值时达到最佳插值效果;而X方向收敛较慢,在10阶插值时达到最佳插值效果。在计算效率上,Newton插值方法比Lagrange插值方法节约了大约1/3的时间。
对于其他IGSO卫星,通过计算得知最佳收敛阶数大多分布在8~10阶。
3)MEO卫星。BDS在轨工作卫星有4 颗中圆地球轨道(medium Earth orbit,MEO)卫星[6]。选取C11号卫星为案例进行插值分析,如表4所示。

表3 C06卫星插值结果 mm

表4 C11卫星插值结果 mm
MEO卫星是3类卫星中收敛速度最慢的卫星。3个方向最佳收敛阶数产生较大差异,X方向在11阶达到最佳,Y方向在10阶达到最佳,而Z方向收敛较快,在8阶达到最佳。阶数的增加对效果没有产生更好的提高,多在mm级震荡。MEO卫星和GPS卫星轨道相近,但与众多关于GPS卫星轨道插值的文献比较发现[9-11],GPS卫星轨道插值最优收敛阶在8~9阶。在计算效率上,Newton插值方法更节约时间。
其他MEO卫星收敛较慢,最佳收敛阶数在10~11阶,高阶后产生震荡。
4 结束语
通过利用2种插值方法对3类BDS卫星精密星历进行内插,数据结果分析得出如下结论:
1)对BDS精密星历进行内插,充分利用待插节点前后的数据信息能够充分体现待插节点附近卫星运动的基本规律,插值精度较高。
2)BDS不同类型轨道的卫星要达到最优收敛效果,应用的内插阶数不同。GEO卫星收敛最快,最佳收敛阶数大多分布在6~7阶;IGSO卫星收敛较慢,最佳收敛阶数大多分布在8~10阶;MEO卫星收敛最慢,最佳收敛阶数在10~11阶。Lagrange方法随着插值阶数的增大,舍入误差会造成龙格现象的出现。因此插值阶数越高,插值效果不一定更好。
3)对于2种插值方法,从插值精度上来说2者插值效果几乎一样;在编程实现上,Lagrange插值方法原理简单易懂,更易于编程;从运算效率上来说Newton插值方法更节约时间,对于大数据计算而言,建议采用Newton插值方法,这样也避免了龙格现象。
[1]杨元喜.BDS卫星导航系统的进展、贡献与挑战[J].测绘学报,2010,39(1):1-6.
[2]李征航,黄劲松.GPS测量与数据处理[M].武汉:武汉大学出版社,2005:17-28.
[3]魏二虎,柴华.GPS精密星历插值方法的比较研究[J].全球定位系统,2006,31(5):13-15.
[4]李庆杨,关治,白峰衫.数值计算原理[M].北京:清华大学出版社,2000:5-20.
[5]龚纯,王正林.MATLAB语言常用算法程序集[M].电子工业出版社,2010:30-40.
[6]施闯,赵齐乐,李敏,等.北斗卫星导航系统的精密定轨与定位研究[J].中国科学:地球科学,2012,42(6):854-861.
[7]ASHKENAZI V,CHEN W,HILL C J,et al.Real-time autonomous orbit determination of LEO satellites using GPS[C]//The Institute of Navigation(ION).Proceedings of the 10th International Technical Meeting of the Satellite Division of the Institute of Navigation,Proceedings of -97.Kansas City,Missouri:ION,1997:16-19.
[8]徐天河,贺凯飞.顾及系统误差的GEO卫星几何法定轨[J].大地测量与地球动力学,2009,29(1):64-69.
[9]蔡艳辉,程鹏飞,李夕银.卫星坐标的内插和拟合[J].全球定位系统,2003,28(3):10-13.
[10]何玉晶,杨九.基于拉格朗日插值方法的GPS IGS精密星历值分析[J].测绘工程,2011,20(5):60-62.
[11]洪樱,欧吉坤,彭碧波.GPS卫星精密星历和钟差三种内插方法比较[J].武汉大学学报·信息科学版,2006,31(6):516-518.
Analysis on BDS satellite precise ephemeris interpolation in different orbits
LI Xiaoguang1,2,CHENG Pengfei2,CHENG Yingyan2
(1.School of Geomatics,Liaoning Technical University,Fuxin,Liaoning 123000,China;2.Chinese Academy of Surveying and Mapping,Beijing 100830,China)
In order to further study on using BDS satellite ephemeris to obtain accurate orbital position with higher sampling rate,the paper used Lagrange and Newton interpolation to interpolate three types of BDS satellite orbits in this paper,and analyzed the feasibility of the two algorithms on the three types of satellites.Result showed that for getting the best effect of convergence,the convergence orders used with the satellites should be different,as the GEO optimal convergence in order 6~7,IGSO in 8~10,and MEO in 10~11 orders.
BDS;precise ephemeris;Lagrange interpolation;Newton interpolation;GEO
2016-04-21
国家自然科学基金项目(41374014);中国测绘科学研究院基本科研业务费支持项目(7771405)。
李晓光(1991—),男,山东滨州人,研究研究生,研究方向为北斗双差等科研和应用。
10.16547/j.cnki.10-1096.20160307.
P228
A
2095-4999(2016)03-0031-04
引文格式:李晓光,程鹏飞,成英燕.BDS卫星精密星历中不同类型轨道的插值分析[J].导航定位学报,2016,4(3):31-34.(LI Xiaoguang,CHENG Pengfei,CHENG Yingyan.Analysis on BDS satellite precise ephemeris interpolation in different orbits[J].Journal of Navigation and Positioning,2016,4(3):31-34.)
