基于RTD可编程逻辑门的数字电路3层网络综合算法

2016-09-16姚茂群许聪源沈继忠

浙江大学学报（理学版） 2016年5期

关键词：汉明隐层向量

姚茂群, 杨　凯, 许聪源, 沈继忠

(1. 杭州师范大学国际服务工程学院, 浙江杭州 311121； 2. 浙江大学信息与电子工程学院，浙江杭州 310027)

基于RTD可编程逻辑门的数字电路3层网络综合算法

姚茂群1, 杨凯1, 许聪源2, 沈继忠2

(1. 杭州师范大学国际服务工程学院, 浙江杭州 311121； 2. 浙江大学信息与电子工程学院，浙江杭州 310027)

随着集成电路的不断发展，CMOS器件的工艺逐渐达到其物理设计极限，研究新器件和新设计方法成为集成电路继续发展的必经之路. 阈值逻辑门因具有强大的逻辑功能而备受关注，共振隧穿二极管(RTD)因其负阻特性在设计阈值逻辑门时更具优势. 由于阈值逻辑门与二进制神经元模型有相似之处，因此可用神经网络模型实现逻辑函数，从而为电路设计提供新的思路. 对基于RTD可编程逻辑门的3层网络算法中的隐层综合算法进行了改进，提出采用汉明距离最大优先覆盖的方法对真向量进行覆盖，从而提高了真向量的覆盖效率，减少了隐层函数个数，并采用真假向量标记的方法简化了隐层综合算法.提出的算法比原隐层综合算法简单，进一步简化了基于RTD可编程逻辑门实现n变量函数的电路.

阈值逻辑门；RTD可编程逻辑门；综合算法

Journal of Zhejiang University(Science Edition), 2016,43(5):567-572,579

随着集成电路的不断发展，互补金属氧化物半导体CMOS制造工艺逐渐逼近其物理极限，为了使集成电路继续按照摩尔定律发展下去，研究新器件和新设计方法成为必经之路[1-2]. 共振隧穿器件(resonant tunneling devices，RTD)比CMOS器件拥有更优秀的性能和特性，具有负内阻、高频高速、自锁、低功耗以及实现功能丰富等特点[3-4]. 阈值逻辑门因具有强大的逻辑功能且独自构成完备集而备受关注，而用RTD器件设计阈值逻辑门更具优势[5-6]. 由于阈值逻辑门与人工神经网络中的二进制神经元模型有相似之处，可用神经网络模型实现逻辑函数，文献[7-9]提出用二进制神经网络实现逻辑函数的计算，然而这些算法得到的阈值函数输入权值和阈值取值范围非常大，不利于硬件电路的实现. 文献[10]提出一种基于RTD的新的可编程逻辑门电路RTD-PLG(RTD-programmable logic gate)，并且提出了基于RTD-PLG的函数综合算法. 虽然用RTD可编程逻辑门RTD-PLG可实现任意n变量函数，但其综合算法存在算法效率低、运算速度慢、设计的电路相对复杂等不足[10-11]. 针对以上问题，本文提出新的3层网络综合算法，为RTD可编程逻辑门RTD-PLG实现n变量逻辑函数提供更优的综合算法，并可简化电路.

1　RTD可编程逻辑门和3层网络

1.1RTD可编程逻辑门

文献[10]设计了一种RTD可编程逻辑门RTD-PLG，可用于实现任意n变量逻辑函数.此电路由MOBILE结构[12]和2n个输入分支构成，其中n个输入分支与驱动RTD并联，称为正输入端，另外n个输入分支与负载RTD并联，称为负输入端. 其电路图及符号如图1所示，输入输出关系可表示为：

(1)

图1　RTD可编程逻辑门Fig.1　Universal threshold logic gate

1.23层网络结构

人工神经网络中的二进制前向神经网络由输入层、隐层和输出层[13]3层结构组成，如图2所示. 文献[10]用此结构实现任意n变量逻辑函数，输入层电路由二输入RTD-PLG组成，用以对输入信号进行整形，确保经过这层的所有输出时序一致；隐层电路由多个RTD-PLG组成，实现函数所需的逻辑功能；输出层电路由1个RTD-PLG组成，用来处理隐层输出，得到最后的输出结果.

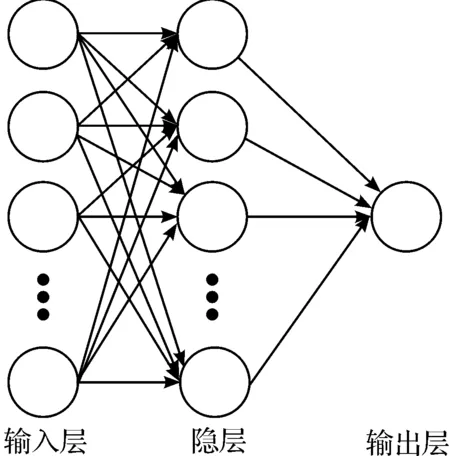
图2　3层网络结构Fig.2　Structure of three layers network

1.33层网络综合算法中的定理与概念

1.3.1真假向量

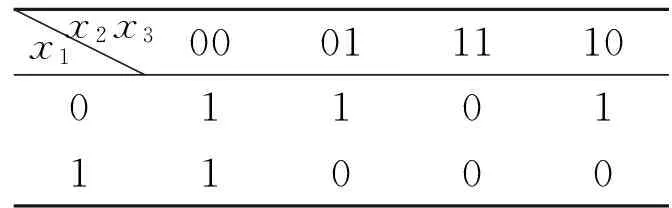
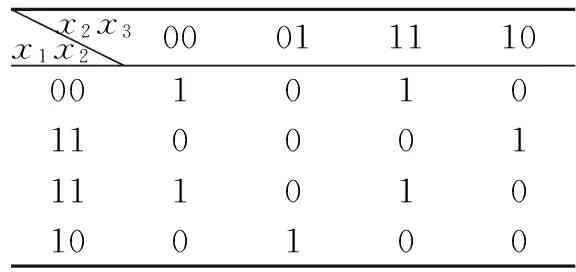
x1x2x3000111100110111000

图33变量函数的卡诺图

Fig.3Karnaugh map of three-variable function

1.3.2汉明距离

2个输入向量之间相异输入变量的个数称为汉明距离，记为dj[14]. 图3所示函数中，向量X0=(0,0,0)和X2=(0,1,0)的汉明距离为d1=1，向量X2=(0,1,0)和X4=(1,0,0)的汉明距离为d2=2.

1.3.3覆盖

选择一个输入向量，与其汉明距离小于等于d(0≤d≤n)的所有输入向量(包括所选择的输入向量)称为被此向量以汉明距离d所覆盖. 图3函数中，向量X0=(0,0,0)，以汉明距离1进行覆盖，覆盖的向量有X0=(0,0,0)，X1=(0,0,1)，X2=(0,1,0)，X4=(1,0,0).

定理1[14]选择一个真向量Xi作为核心向量，如果满足与其汉明距离小于等于d(0≤d≤n)的所有输入向量均为真向量，那么这些向量(包括核心向量)可以表示为f(X)=1,当w1x1+w2x2+…+wnxn≥T.

(2)

其中，ωi为权值，T为阈值，可由下式得到：

(3)

1.3.4抑制向量

将某些假向量暂时看作真向量，从而使部分真向量满足定理1，这些假向量称为抑制向量[14].

2　改进的3层网络算法

3层网络算法中最主要的为隐层算法，通过寻找核心向量和确定汉明距离，最终覆盖所有的真向量，并使用抑制向量纠正在覆盖过程中覆盖的假向量，以实现所需的逻辑功能. 文献[10]提出的基于RTD-PLG的3层网络综合算法已很好地覆盖了所有真向量，不足之处在于：(1)在选择了核心向量或者抑制向量后，采用以汉明距离从小到大的覆盖方法对真向量进行覆盖，使得覆盖真向量的速度较慢，从而降低了算法效率. (2)当使用抑制向量纠正在覆盖真向量的过程中同时被覆盖的假向量时，选择的抑制向量数量过多，导致隐层函数数量也过多.

文献[10]用HSPICE对电路的正确性进行了仿真论证，本文对其隐层综合算法做了改进，提出了新的3层网络综合算法. 为使算法表述更统一，本文综合了核心向量与抑制向量的概念，消除了核心向量为真向量的约束. 为提高算法的效率，在选择了核心向量后，采用以汉明距离从大到小的覆盖方法对真向量进行覆盖，即选取离核心向量最远的真向量的汉明距离作为初始距离对真向量进行覆盖，并采用可重叠覆盖方式选择核心向量，即核心向量可重复选择，相同的核心向量以不同的汉明距离分别对真向量进行覆盖. 为方便阅读，算法中变量符号定义如下：

n：函数的变量数.

Xi：函数的第i个输入向量.

tagi：输入向量Xi的真假标记.

hi：记录每个tagi被修改的次数.

dj：第j次覆盖的汉明距离.

rj：第j次覆盖后，被覆盖的tagi=1的向量个数.

wj：第j次覆盖后，被覆盖的tagi=0的向量个数.

fi：核心向量Xi所对应的隐层函数.

ki：核心向量Xi所对应的隐层函数的权值.

改进的基于RTD-PLG的3层网络综合算法步骤：

步骤1标记待综合实现的n变量函数所有输入向量Xi，若为真向量，则标记tagi=1，若为假向量，则tagi=0. 每个标记对应1个修改次数参量hi=0.

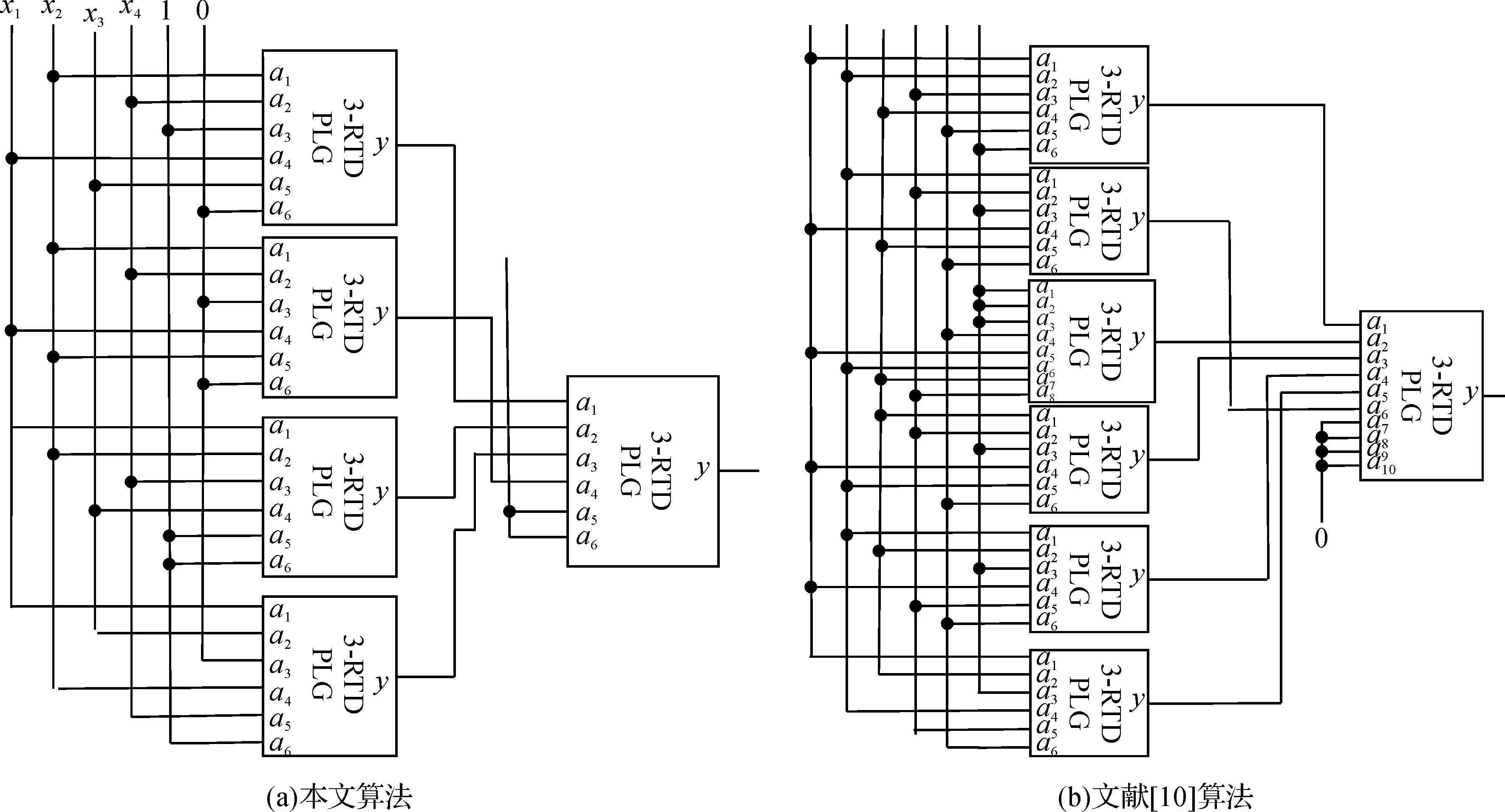
步骤3计算核心向量Xi覆盖的向量中tagi=1和tagi=0的向量个数rj和wj，若rj

步骤4修改核心向量Xi所覆盖的所有向量的tagi：若被覆盖的向量为真向量，则修改其标记tagi=0，若被覆盖的向量为假向量，则修改其标记tagi=1.

步骤5对所有修改过标记的向量所对应的hi进行加1计数.

步骤6重复步骤2至5，直到所有输入向量的标记tagi=0为止.

步骤7所有被确定的核心向量Xi所对应的隐层函数fi，可由式(2)和(3)计算得到.

步骤8最终的输出层函数则为

例1中函数f的卡诺图如图4所示，用新的3层网络综合算法实现，步骤如下：

x3x4x1x2 00011110001010010001111110100101

图4例1函数f的卡诺图

Fig.4Karnaugh map of example 1

步骤1标记所有输入向量.

步骤3修改被覆盖的向量的标记，tagi=0(i=0,3,6,9,12,13,15),tagi=1(i=1,4,5,7). 对所有修改的标记进行加1计数，hi=1(i=0,1,3,4,5,6,7,9,12,13,15).

步骤4以汉明距离d=2重新搜索所有输入向量，因无法确定核心向量，所以汉明距离减1，即以汉明距离d2=1对所有输入向量进行搜索，发现假向量X5=(0,1,0,1)覆盖的向量中tagi=1的个数最多，为4个，分别为X1=(0,0,0,1)，X4=(0,1,0,0)，X5=(0,1,0,1)，X7=(0,1,1,1)，同时X5=(0,1,0,1)也覆盖了1个向量X13=(1,1,0,1). 因为3>1，所以可再次确定X5=(0,1,0,1)为核心向量. X5=(0,1,0,1)所对应的标记修改次数h5=1为奇数，则对应的隐层函数权值k2=-1.

步骤5修改被覆盖的向量的标记，tagi=1(i=13)，tagi=0(i=1,4,5,7). 对所有修改的标记进行加1计数，hi=2(i=1,4,5,7,13).

步骤6以汉明距离d=1重新搜索所有输入向量，因无法确定核心向量，所以汉明距离再减1，即以汉明距离d3=0，确定真向量X13=(1,1,0,1)和X10=(1,0,1,0)为核心向量，所对应的标记修改次数h13=2，为偶数，h10=0，也为偶数，则对应的输出函数权值k3=1和k4=1.

步骤7修改标记后所有的向量标记tagi=0，根据式(2)和(3)可得对应的隐层函数为：

f1(X)=1,-x1+x2-x3+x4≥0.

(4)

f2(X)=1,-x1+x2-x3+x4≥1.

(5)

f3(X)=1,x1+x2-x3+x4≥3.

(6)

f4(X)=1,x1-x2+x3-x4≥2.

(7)

步骤8输出层函数为

(8)

总共经过4次搜索，选择了4个核心向量完成所有真向量的覆盖，依次覆盖真向量的个数为7和1，得到4个隐层函数. 根据式(1)和式(4)～(8)以及图2所示结构，用RTD-PLG实现例1函数f的电路如图5(a)所示，其中用了5个RTD-PLG门. 而文献[10]的算法则选择X13=(1,1,0,1)为核心向量，以汉明距离d1=1对真向量进行覆盖，一次只能覆盖4个真向量，同时覆盖了1个假向量X5=(0,1,0,1)，选择X5=(0,1,0,1)作为抑制向

图5　例1函数f基于RTD-PLG的电路实现Fig.5　RTD-PLG implementation of example 1

量修正假向量X5=(0,1,0,1)，再选择X0=(0,0,0,0)，X3=(0,0,1,1)，X6=(0,1,1,0)和X10=(1,0,1,0)为核心向量，以汉明距离都为0覆盖剩下的真向量，选择了5个核心向量和1个抑制向量，总共经过6次搜索完成所有真向量的覆盖，覆盖真向量的个数依次为4，1，1，1和1，得到6个隐层函数，用RTD-PLG实现例1函数f的电路图如图5(b)所示，用了7个RTD-PLG门. 2种算法都没有计算输入层的4个二输入RTD-PLG构成的整形电路，本文算法比文献[10]算法少用了2个RTD-PLG门，电路更简单.

函数f的卡诺图如图6所示，用新的3层网络综合算法实现，步骤如下：

x1x2x2x300011110001010110001111010100100

图6例2函数f的卡诺图

Fig.6Karnaugh map of example 2

步骤1以汉明距离d1=2搜索所有输入向量，确定X5=(0,1,0,1)为核心向量，被覆盖的向量中，6个向量的tagi=1(i=0,3,6,9,12,15)，5个向量的tagi=0(i=1,4,5,7,13). X5=(0,1,0,1)所对应的标记修改次数h5=0，为偶数，则对应的隐层函数权值k1=1.

步骤2修改被覆盖的向量的标记，tagi=0(i=0,3,6,9,12,15)，tagi=1(i=1,4,5,7,13). 对所有修改的标记进行加1计数，hi=1(i=0,1,3,4,5,6,7,9,12,13,15).

步骤3以汉明距离d2=1搜索所有输入向量，再次确定X5=(0,1,0,1)为核心向量，被覆盖的向量中，5个向量的tagi=1(i=1,4,5,7,13)，无tagi=0向量. X5=(0,1,0,1)所对应的标记修改次数h5=1，为奇数，则对应的隐层函数权值k2=-1.

步骤4修改标记后所有的向量标记tagi=0，根据式(2)和(3)，可得对应的隐层函数为：

f1(X)=1,-x1+x2-x3+x4≥0.

(9)

f2(X)=1,-x1+x2-x3+x4≥1.

(10)

步骤5输出层函数为

(11)

例2函数总共经过2次搜索，选择了2个核心向量完成所有真向量的覆盖，并一次覆盖了所有的真向量，得到2个隐层函数. 根据式(1)和式(9)～(11)以及图2所示结构，用RTD-PLG实现例2函数f的电路，只需要3个RTD-PLG门. 文献[10]算法选择了2个核心向量和4个抑制向量，总共经过6次搜索完成了所有真向量的覆盖，覆盖真向量的个数依次为3和3，得到6个隐层函数，需要7个RTD-PLG门实现此函数. 同样2种算法都没有计算输入层电路，本文算法比文献[10]算法少用了4个RTD-PLG门，实现的电路更简单.

研究发现，若函数f以某一输入向量为核心向量，真向量和假向量分别围绕此核心向量以不同的汉明距离分布，满足这种分布的函数用新的3层网络综合算法实现最为简单，观察例2函数f后发现，以输入向量X=(0,1,0,1)为核心向量，真向量以汉明距离d=2围绕核心向量分布，假向量以汉明距离d=1围绕核心向量分布.例2函数正好满足此分布，因此电路特别简单.

例3使用RTD-PLG电路实现5变量偶校验函数.

例3的5变量偶校验函数卡诺图如图7所示，用新的3层网络综合算法，其实现步骤如下：

x3x4x5x1x2 0000010110101101111011000001010101011010101011010101011010101010

图7例3的5变量偶校验函数卡诺图

Fig.7Karnaugh map of example 3 with 5 variables

步骤1以汉明距离d1=3搜索所有输出向量，确定X30=(1,1,1,1,0)为核心向量，被覆盖的向量中，12个向量的tagi=1(i=2,7,11,13,14,19,21,22,25,26,28,31)，8个向量的tagi=0(i=6,10,15,18,23,27,29,30).X30=(1,1,1,1,0)所对应的标记修改次数h30=0为偶数，则对应的隐层函数权值k1=1.

步骤2修改被覆盖的向量的标记，tagi=0(i=2,7,11,13,14,19,21,22,25,26,28,31)，tagi=1(i=6,10,15,18,23,27,29,30). 对所有修改的标记进行加1计数，hi=1(i=2,6,7,10,11,13,14,15,18,19,21,22,23,25,26,27,28,29,30,31).

步骤3以汉明距离d2=2搜索所有输入向量，再次确定X30=(1,1,1,1,0)为核心向量，被覆盖的向量中，8个向量的tagi=1(i=6,10,15,18,23,27,29,30)，4个向量的tagi=0(i=14,22,26,31). X30=(1,1,1,1,0)所对应的标记修改次数h30=1为奇数，则对应的隐层函数权值k2=-1.

步骤4修改被覆盖的向量的标记，tagi=0(i=6,10,15,18,23,27,29,30)，tagi=1(i=14,22,26,31). 对所有修改的标记进行加1计数，hi=2(i=6,10,14,15,18,22,23,26,27,29,30,31).

步骤5以汉明距离d3=1搜索所有输入向量，再次确定X30=(1,1,1,1,0)为核心向量，被覆盖的向量中，4个向量的tagi=1(i=14,22,26,31)，1个向量的tagi=0(i=30)，同时确定X0=(0,0,0,0,0)也为核心向量，被覆盖的向量中，4个向量的tagi=1(i=1,4,8,16)，1个向量的tagi=0(i=0). X30=(1,1,1,1,0)所对应的标记修改次数h30=2为偶数，则对应的隐层函数权值k3=1，X0=(0,0,0,0,0)所对应的标记修改次数h0=0为偶数，则对应的隐层函数权值k4=1.

步骤6修改被覆盖向量的标记，tagi=0(i=14,22,26,31)，tagi=1(i=30)，tagi=0(i=1,4,8,16)，tagi=1(i=0). 对所有修改的标记进行加1计数，hi=3(i=14,22,26,30,31)，hi=1(i=0,4,8,16).

步骤7以汉明距离d4=0搜索所有输入向量，再次确定X30=(1,1,1,1,0)和X0=(0,0,0,0,0)为核心向量，对应的隐层函数权值为k5=-1和k6=-1.

步骤8修改标记后的所有向量的标记为tagi=0，根据式(2)和(3)可得对应的隐层函数：

f1(X)=1,x1+x2+x3+x4-x5≥1.

(12)

f2(X)=1,x1+x2+x3+x4-x5≥2.

(13)

f3(X)=1,x1+x2+x3+x4-x5≥3.

(14)f4(X)=1,-x1-x2-x3-x4-x5≥-1.

(15)

f5(X)=1,x1+x2+x3+x4-x5≥4.

(16)

f6(X)=1,-x1-x2-x3-x4-x5≥0.

(17)

步骤9输出层函数为

(18)

例3函数总共经过6次搜索，选取了6个核心向量完成所有真向量的覆盖，覆盖真向量的个数依次为12和4，得到6个隐层函数，根据式(1)和式(12)～(18)以及图2所示结构，用RTD-PLG实现例3的5变量偶校验函数的电路，需要7个RTD-PLG门. 文献[10]的算法选取了4个核心向量和4个抑制向量，经过8次搜索完成所有真向量的覆盖，覆盖真向量的个数依次为4，4，4和4，得到8个隐层函数，需要9个RTD-PLG门.2种算法都没有计算输入层电路，本文算法比文献[10]算法少用2个RTD-PLG门，电路更简单.

采用汉明距离最大优先覆盖的方法，以每次覆盖尽可能多的真向量为原则，加快了覆盖真向量的速度，从而减少了搜索的步骤和选择核心向量的次数，并且在实现相同函数时减少了隐层函数的个数，因此，使用RTD-PLG实现n变量函数的电路更简单. 因新算法只利用汉明距离对所要实现的函数进行搜索覆盖，没有多余步骤，所以算法相对简单，并能保证电路设计的正确性.

3　结　论

提出了一种基于RTD可编程逻辑门的新3层网络综合算法，此算法省去了抑制向量的概念，消除了核心向量必须为真向量的限制，使其表述更统一；采用汉明距离最大优先覆盖的方法，提高了真向量覆盖的速度以及算法的搜索覆盖效率；通过减少核心向量的数量，从而减少了隐层函数的个数，使设计的电路更简单. 本文算法运用了真假标记的方法对所有输入向量进行处理，只需要做重复的搜索覆盖工作，算法更简单，利于计算机编程实现. 研究发现，当函数以某一输入向量为核心向量，真假向量分别以不同的汉明距离围绕核心向量分布时，用本文算法实现n变量函数，算法效率最高、电路设计最简单. 新的3层网络综合算法在计算效率和综合结果两方面都较原算法优良，为用RTD可编程逻辑门实现n变量函数提供了更好的方法，使基于RTD-PLG设计的逻辑电路更简单.

[1]IWAIH.MaterialsandstructuresforfuturenanoCMOS[C]// Proceeding of Nanotechnology Materials and Devices Conference. Jeju: IEEE Press,2011:14-18.

[2]HARIHARAN A N, PONTARELLI S, OTTAVI M, et al. Modeling open defects in nanometric scale CMOS[C]// Proceeding of Defect and Fault Tolerance in VLSI Systems. Kyoto: IEEE Press,2010:249-257.

[3]MURAMATSU N, OKAZAKI H, WAHO T. A novel oscillation circuit using a resonate-tunneling diode[C]// Proceeding of Circuits and Systems. Kobe:IEEE Press, 2005:2341-2344.

[4]ZHENG Yexin, HUANG Chao. Complete logic functionality of reconfigurable RTD circuit elements[J]. IEEE Transactions on Nanotechnology,2009,8(5):631-642.

[5]韦一,沈继忠.基于阈值逻辑的逻辑函数综合算法研究[J].电子与信息学报,2011,33(7):1775-1778.

WEI Yi, SHEN Jizhong. Research of logic function synthesis algorithm based on threshold logic[J]. Journal of Electronics & Information Technology,2011,33(7):1775-1778.

[6]MIRHOSEINI S M, SHARIFI M J, BAHREPOUR D. New RTD-based general threshold gate topologies and application to three-input XOR logic gates[J]. Journal of Electrical and Computer Engineering,2010,35(1):1-4.

[7]杭国强,李锦煊,王国飞.新型钟控神经元MOS采样/保持电路[J].浙江大学学报:工学版,2012,46(2):333-337.

HANG Guoqiang, LI Jinxuan, WANG Guofei. A novel sample and hold circuit using clocked neuron-MOS scheme[J].Journal of Zhejiang University:Engineering Science,2012,46(2):333-337.

[8]WANG D, CHAUDHARI N S. An approach for construction of Boolean neural networks based on geometrical expansion[J]. Neurocomputing,2004,57:455-461.

[9]ZHANG Hao, WANG Xingyuan, LIN Xiaohui. Synchronization of boolean networks with different update schemes[J]. IEEE/ACM Transactions on Computational Biology and Bioinformatics,2014,11(5):965-972.

[10]韦一.基于RTD的通用逻辑单元设计及其应用[D].杭州：浙江大学,2011:48-59.

WEI Yi. General Logic Units Design Based on RTD and Its Application[D].Hangzhou:Zhejiang University,2011:48-59.

[11]QUINTANA J M, AVEDILLO M J, PETTENGHI H. Programmable logic gate based on resonant tunneling devices[C]// IEEE International Symposium on Circuits and Systems. Vancouver:IEEE Press, 2004:697-700.

[12]CHEN K, AKEYOSHI, MAEZAWA K. Monolithic integration of resonant tunneling diodes and FET’s for monostable-bistable transition logic elements (MOBILE’s) [J]. Electron Device Letters,1995,16(2):70-73.

[13]GRAY D L, MICHEL A N. A training algorithm for binary feed forward neural networks[J]. IEEE Transactions on Neural Networks,1992,3(2):176-194.

[14]KIM J H, PARK S K. The geometrical learning of binary neural networks[J]. IEEE Transactions on Neural Networks,1995,6(1):237-247.

Three-layers network synthesis algorithm of digital circuits based on RTD programmable logic gates.

YAO Maoqun1, YANG Kai1, XU Congyuan2, SHEN Jizhong2

(1.InstituteofServiceEngineering,HangzhouNormalUniversity,Hangzhou311121,China; 2.CollegeofInformationScience&ElectronicEngineering,ZhejiangUniversity,Hangzhou310027,China)

With the development of integrated circuit, the CMOS technology will face some fundamental physical limittations. The new devices and new design methods thus become very important to the further development of integrated circuit industry. Threshold logic gate has been paid too much attention because of its powerful logic function, and the resonant tunneling diode (RTD) appears to be more suitable for designing the threshold logic gate because of its negative resistance characteristics. As the threshold logic gate and binary neuron model have similar structure, neural network model can be used to implement the logic functions, leading to a new idea for circuit design. In this paper, we improve the hidden layer algorithm of three layers network algorithm based on the RTD programmable logic gate, and propose a method which adopts the biggest distance of Hamming distance in preference to cover the true vector. Our method can improve the coverage efficiency of the true vector, and reduce the number of the hidden layer function. Meanwhile, we use the mark of true vector and false vector to simplify the algorithm. Compared to the original algorithm, the proposed algorithm is concise, and can simplify the circuit of the RTD programmable logic gate to implement thenvariable function.

threshold logic gate; RTD programmable logic gate; synthesis algorithm