微积分思想在物理教学应用中的探讨
2016-09-15牛艳秋
牛艳秋
(吉林建筑大学 城建学院,吉林 长春 130111)
微积分思想在物理教学应用中的探讨
牛艳秋
(吉林建筑大学城建学院,吉林长春130111)
微积分在物理中有着广泛的应用,解决物理问题的过程中有很多数学思想容易被忽略,不利于学生对解题方法的理解和掌握,也是学习物理理论感到困难的重要原因,本文给出了利用数学解题思想来解决物理问题的一点建议.
微积分;物理;微元法
微积分是一种数学思想,微分是“无限细分”,积分是“无限求和”,无限就是极限,因此,极限的思想是微积分的基础,他是用一种运动的思想看待问题.在大学物理中从质点运动学到质点动力学,从功和能到刚体转动,从静电场到稳恒磁场,都要应用微积分来分析解决.因此,微积分在大学物理课程中有着广泛而重要的应用.
在大学物理中应用微积分,不论是教材还是教师讲课很少与微积分中处理变化的量的数学思想(即:分割、近似、取极限的思想)相联系,而是直接写出所研究物理量的微元,然后求微分或积分,这样不利学生对所讲方法的理解和掌握,也是很多人学习物理理论感到困难的一个重要原因.
1 用微积分的方法解决速度和加速度问题
设某物体做变速直线运动时,其运动规律按照我们初中学习的定义会得出:S=υt其中t是时刻,S是位移.下面讨论物体在时刻t0的瞬时速度.当时刻由t0变到t0+△t时,物体的位移由f(t0)变到f(t0+△t).这段时间物体走过的路程为△S=f)其平均速度为.当时间间隔很小时可以看成物体在时刻t0的速度的近似值.△t越小,近似程度越高,把当△t→0时的平均速度的极限值成为该物体在时刻t0的瞬时速度(也称速度)即:
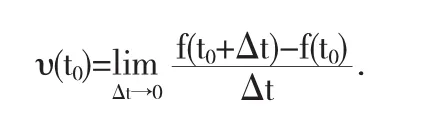
再如在研究匀变速直线运动时,速度均匀变化,速度变化快慢的物理量加速度就可以将△t→0的平均加速度的极限值称为该物体在t0时刻的瞬时加速度(也称加速度)表示为
通过上述内容我们可以看出,整个过程中我们就是通过分割、近似、取极限的思想来将质点的位移△S与完成这段位移所需的时间△t的比值取极限来得到速度和加速度的瞬时值,也就是利用的导数概念,此时学生才能够在物理中融入数学思想可让学生更好的理解和掌握物理概念.
2 用微积分方法解决变力作功的问题
在力学、热力学中经常会有求变力作功的问题.例如:从10m深的井中,把10kg的水匀速上提,设每升高1m漏去0.2kg水(.1)画出示意图,设置坐标轴后,写出外力所作功元的表示式;(2)计算把水从水面提高到井口外力所作的功.
求变力作功的实质就是先把物体的运动轨迹分成许许多多小位移元求出功元,然后求总功
根据上述,首先假设井水水面到地面的距离h不因提水而改变.在水面上建立坐标原点,竖直向上为y轴正向,建立坐标系如图1,则有漏水率为当水桶上升的高度为y时,桶中水的质量为(10-0.2y)kg.水桶匀速上升,提升力F应等于水桶重量,即F=(10-0.2y)g.由y处再上升d y高度,F可视为不变,则提升力(外力)所作功元为:
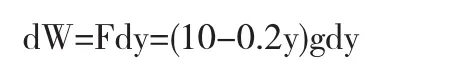

图1
把水从水面提到井口外力所作功:

在计算的过程中,先简单地给出所研究的物理量的微元,再求微分和积分来解答所求的问题.运用数学思想解决上述问题首先考虑微元的选取是怎样来的,我们通过微积分方法把大学物理中变化的量转化为不变的量,将位移S分割成无数个小位移元d s看成是一点,其中F为不变量,由W=F·s可知这一点的功元就得,功元求出后,对无数个点求和,也就是积分,进一步求出变力在整个物理过程中做的总功.
3 用微积分方法解决刚体转动问题
使用微积分解决物理中的问题,同样遵循最基本的数学思想,取微元是计算各种积分的基础,解题过程中直接给出公式那有的同学就会疑问这个公式是怎样来的,运用数学思想,我们将小棒分割,近似的把每一段看成一个点,那么在这一点上我们所要求的转动惯量就为r2d m,整个棒上的转动惯量就是对无数个点的转动惯量求和,即求积分,就得出在刚体转动问题中它是非常重要的,首先要保证在选取的微元内能近似处理成简单基本的物理模型,以便于分析物理问题;其次要尽量把微分元选取的大,这样可使积分运算更加简单,以便于解决物理问题.
例如求质量为m,长为l的均匀细棒对下面两种给定的转轴的转动惯量.
(1)转轴通过棒的中心并与棒垂直;
(2)转轴通过棒的一端并与棒垂直.

图2

4 用微积分解决电磁学的问题

图3
(1)求带电直线周围一点p的电场强度问题,就是先把带电直线分成许许多多小电荷元d q,求出各电荷元在p点的电场强度元,整个带电直线在p点的总电场(如图3)
用数学形式来表示大学物理中的物理现象和规律具有明确意义,使用微分来表示物理量和物理公式,使得问题由复杂变得简单化.
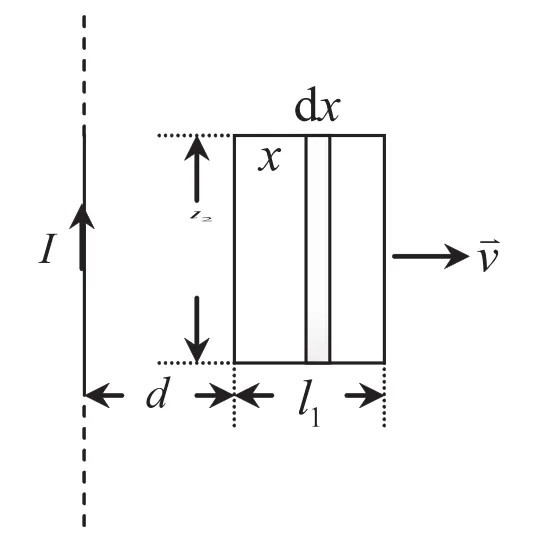
图4
如图4所示,在一无限长直载流导线的近旁放置一矩形导体线框.该线框在垂直于导线方向上以匀速率v向右运动.求在图示位置处线框中的感应电动势的大小.
解1当闭合导体线框在磁场中运动时,线框中的总电动势就等于框上各段导体中的动生电动势的代数和.导体框中水平两段上的电动势为零,可求竖直两段的电动势,和即为总的电动势.则总的电动势为:
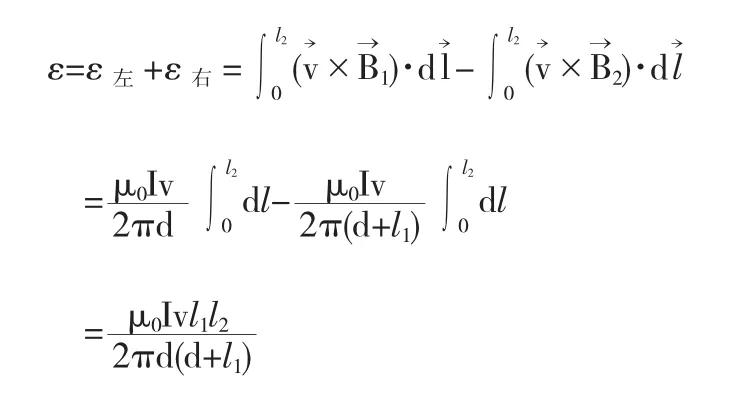
先求任意时刻穿过线框的磁通量Ø,再求电动势ε.
设顺时针方向为线框回路的正向.在任意处距导线y处(即设图中的d为一般值y),穿过线框的磁通量为

当y=d时,得线框在图示位置处的电动势为

由ε>0可知,线框中电动势的方向为顺时针方向.
从上面的例子可以看出积分微元的选取不唯一,在每一种积分微元中近似成的物理模型是不同的,不管选取怎样的微元来分析计算,其结果都相同,都是问题的精确解.这也体现了微积分分析方法的神奇之处,由于积分微元无限趋于零,使得由有限范围内的近似到无限小范围内的精确,完成了问题的精确求解.
通过几个例题的解法,我们可以看出这几种物理问题的解题方法是与数学思想紧密相联的.总的解题方法都是围绕着分割、近似、取极限,然后在求微分或积分的思路来推广.微积分在物理中有着不同的应用,范围广泛,我们熟练掌握并深刻理解微积分的概念,为各门学科的学习奠定良好的基础.
〔1〕梁小佳.微积分在大学物理中的应用探究[J].甘肃高师学报,2010,15(2):78-80.
〔2〕祝之光.物理学[M].北京:高教出版社,2006.
〔3〕祝之光.物理学习题分析与解答[M].北京:高教出版社,2008.
〔4〕王千.高等数学学习指导[M].长春:吉林大学出版社,2010.
O411
A
1673-260X(2016)08-0011-03
2016-04-16
