含定积分的等式与不等式的证明
2016-09-15王旭丹
苏 丽,王旭丹
(大连科技学院 基础部,辽宁 大连 116052)
含定积分的等式与不等式的证明
苏丽,王旭丹
(大连科技学院基础部,辽宁大连116052)
文章列举了多种证明方法,包括利用定义,利用性质,利用积分中值定理,许瓦兹不等式,变上限积分,泰勒公式等来完成含有积分的等式和不等式的证明问题.
定积分;等式;不等式;证明
在教学过程中会遇到很多含有定积分的证明题,由于题型多样,所以解决起来需要一定的技巧.但其根本点是将数值问题归结为函数问题,利用微积分的理论研究函数的性质,再根据函数的性质和特点来完成证明过程.
1 预备知识
1.1定积分的定义

1.2积分中值定理
若f(x)在[a,b]连续,则至少存在一点ξ∈(a,b)使得
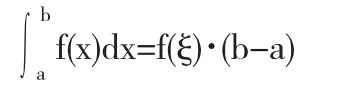
1.3积分估值不等式
1.4许瓦兹不等式
设f(x)与g(x)在[a,b]可积,
1.5牛顿莱布尼兹公式

1.6泰勒公式

2 含有定积分的等式证明
例1设f(x)在[a,b]正连续,且f(x)最大值为M,
分析结论要证明极限值为f(x)的最大值,想到了利用两边夹法则,
证明因为f(x)在[a,b]正连续,所以存在x0∈[a,b],使得f (x0)=M.
且∀ε>0,∃δ>0,使得M-ε<f(x)<M+ε,当x∈(x0-δ,x0+δ)
由ε任意性,令ε=0有

对上式取极限
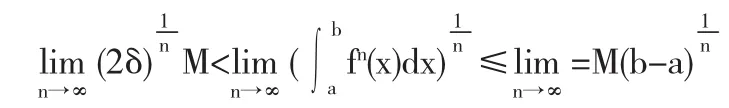
例2设f(x)在[a,b]非负连续且严格单调递减,对于任意的n,存在ξn∈[a,b]使得
分析此题结论形似积分中值定理,可利用题中提到的单调性.
因此有
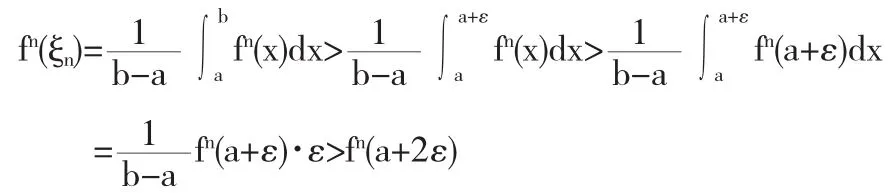
又f(x)严格单调递减,有a≤ξn≤a+2ε,所以
3 含有定积分的不等式证明
3.1利用许瓦兹不等式证明
分析因要证结论中被积函数是乘积的形式,考虑用许瓦兹不等式.
证明由已知条件(f x)在[a,b]上可导,∃x0∈[a,b]使得f(x)=M,又因为f'(x)在[a,b]连续,利用牛顿莱布尼兹公式有

已知f(a)=0及许瓦兹不等式有

3.2利用积分中值定理证明
例4设f(x)定义在[a,b],且∀x∈[a,b],f'(x)≥m>0,
分析要证明的不等式有m,而f'(x)≥m>0,因此考虑将左面的积分与f'(x)联系起来,此时还可以积分出来.

3.3利用定积分的定义证明
例5设f(x)在[0,1]连续,且f(x)>0.
分析此题可以利用均值不等式

证明在[0,1]中插入n-1个等分点,

上式两边取极限有

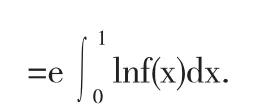
3.4利用变上限积分证明
例6设f(x)在[0,1]连续,且单调递增,
分析课本上利用变上限积分证明出了牛顿-莱布尼兹公式,受此启发我们可以用变上限积分构造辅助函数来解决一些证明问题.

3.5利用泰勒公式证明
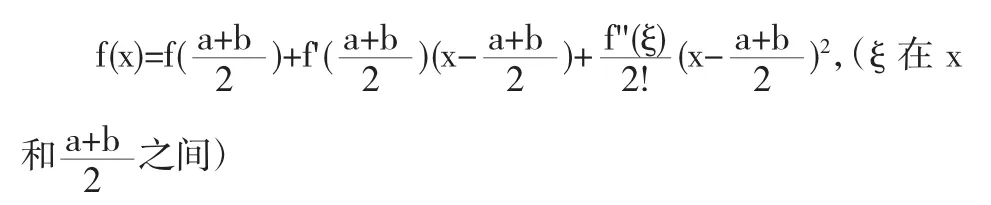
将上面的表达式在[a,b]上积分,
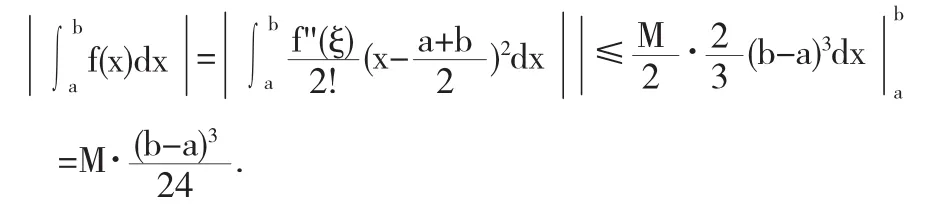
在求解过程中,要善于观察表达式特点,灵活运用所学知识,力求简化证明过程.
〔1〕华东师范大学数学系.数学分析[M].北京:高等教育出版社,2000.
〔2〕同济大学应用数学.高等数学[M]上海:同济大学出版社,2004.
〔3〕刘玉琏,数学分析讲义[M].北京:高等教育出版社,1988.
〔4〕徐利治,王兴华.数学分析的方法及例题选讲[M].北京:高等教育出版社,1983.110-112.
O174
A
1673-260X(2016)08-0007-02
2016-05-11
